EV-BWPT 无缝功率环移相控制策略研究

刘芳，赵杨，李昊，凌淳扬

（合肥工业大学电气与自动化工程学院，合肥 230009）

无线电能传输WPT（wireless power transfer）以其便捷、安全、可靠等优势，被应用于电动汽车EV（electric vehicle）领域，解决了有线充电的绕线焦虑及安全问题[1-3]。目前，WPT 技术的日益成熟及智能电网的快速发展，将电动汽车与电网V2G（vehicleto-grid）相结合，使电动汽车在未来成为一种重要的分布式储能能源，对提升能源互联网的稳定性和智能性有重要作用[4]。但WPT 系统的效率问题成为制约其快速发展的重要因素，如何提高系统传输效率成为学术界的研究热潮。

目前，WPT的研究主要集中在单向传输系统即电网向车载端供电的传输效率[5-6]、信号传输[7-8]及系统传输特性[9-10]等方面,对于双向无线电能传输BWPT（bidirectional wireless power transfer）系统的研究相对较少。文献[11]提到的能量发射端开关管工作在高频逆变状态，能量接收端开关管工作在不控整流状态的控制方式，需要在切换模式下才能实现能量流动方向的改变；文献[12-13]利用有功/无功功率计算得到的功率角控制功率流流动方向，使其在0°时功率正向流动，180°时功率反向流动，同时利用有功功率控制策略控制内移相，进而控制能量传输大小，但并未具体说明如何判断功率流向，在能量流动方向发生变化时存在需要切换的问题，且若将功率角固定在0°/180°，则无法灵活调节移相角，导致变换器工作在非额定状态时系统整体效率下降；文献[14]采用单电流环的方式控制系统能量传输，结构简单，但该方法存在回流功率，降低了系统传输效率；文献[15]采用多自由度组合控制优化双向无线电能传输系统效率的控制策略，即通过有功功率环同时控制原、副边侧内移相以及原副边之间的外移相，但未考虑系统无功功率对效率的影响。

在BWPT 系统的控制策略方面，由于其具有较多的控制自由度，自由度的选取不同会影响传输功率及损耗，从而对系统的效率造成影响，如何通过不同自由度之间的协调配合提高系统效率，是研究BWPT 控制策略的关键。为此，本文提出一种双向无线电能传输系统无缝功率环移相控制策略。首先分析双边LCC 补偿网络无线电能传输系统中功率传输特性；其次，提出了采用有功功率环路控制外移相角，无功下垂环路控制内移相角的无缝功率环移相控制策略，该策略无需切换模式即可实现功率正反向流动；最后，通过仿真和实验验证该控制方案可减少系统无功功率，提高系统效率。

1 双向无线电能传输系统

1.1 系统拓扑结构

与传统的单向WPT 系统不同，BWPT 系统为了满足功率正反向流动，原边与副边均采用全控H桥电路，并采用LCC 高阶补偿网络提高系统传输功率，滤除高频逆变产生的高频分量。典型的双LCC 补偿网络BWPT 系统如图1 所示。

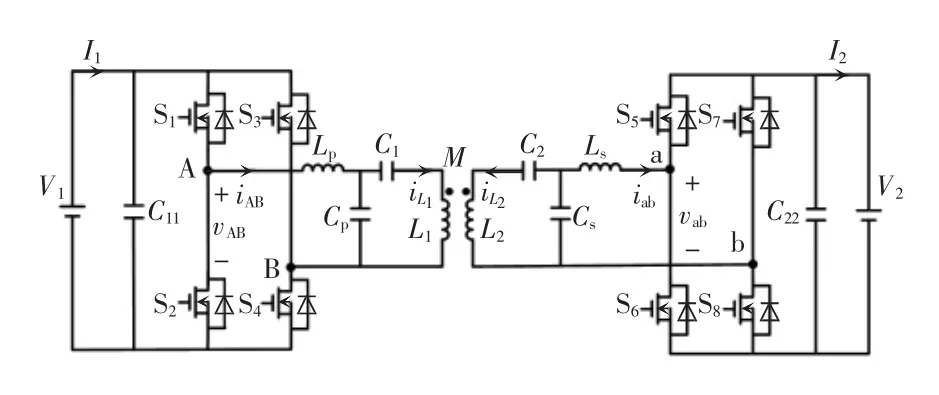
图1 双LCC 补偿网络BWPT 系统拓扑Fig.1 Topology of BWPT system based on bilateral LCC compensation network

图1中，S1～S4、S5～S8分别构成原、副边全控H桥电路,M为线圈间互感，L1和L2为线圈自感，C1和C2为谐振补偿电容，Cp和Cs为谐振电容，Lp和Ls为谐振电感，C11和C22为滤波电容。V1和I1分别为原边直流电压和输入电流，V2和I2分别为副边直流电压和输出电流，vAB和iAB分别为原边变换器端口电压和电流，vab和iab分别为副边变换器端口电压和电流，iL1为原边线圈电流，iL2为副边线圈电流。

1.2 移相控制驱动

移相控制是传统的逆变器控制方法之一，主要控制逆变器的输出电压。所述移相控制就是以50%占空比的方波导通或者关断变换器中的开关管，在驱动波形上存在一个超前或滞后的相位，利用移相调节输出电压大小进而控制输出功率。BWPT 系统移相驱动波形及电路工作波形如图2 所示。

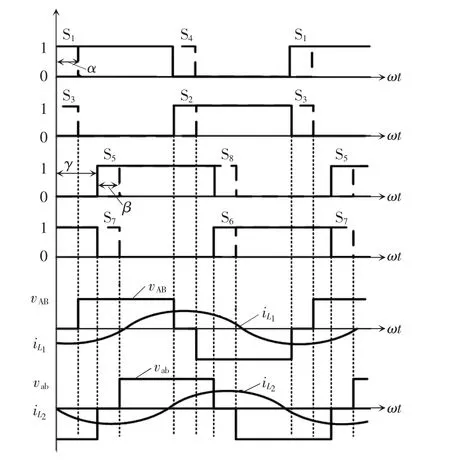
图2 BWPT 系统移相驱动波形及电路工作波形Fig.2 BWPT system phase-shift driving waveform and circuit working waveform

图2为控制BWPT 系统原、副边开关管的驱动波形序列，其中原边侧桥臂对角线开关管（如图中S1和S4）相位差为原边侧内移相角α，副边侧桥臂对角线开关管（如图中S5和S8）相位差为副边侧内移相角β，两侧桥臂对应位置开关管（如图中S1和S5）之间的相位差为外移相角γ。由驱动波形及电路工作波形可知，移相角的改变会影响桥臂侧输出电压的大小。

2 双LCC 谐振网络的BWPT 系统建模

采用基波分析法[15-16]和互感等效模型对系统建模分析，基于LCC 谐振补偿网络的BWPT 系统等效电路如图3 所示。

图3 基于LCC 补偿网络的BWPT 系统等效电路Fig.3 Equivalent circuit of BWPT system bed on LCC compensation network

式中：ω0为系统工作频率；M为原、副边线圈之间的互感。

根据文献[15-16]，由傅里叶级数展开得，原边侧和副边侧全桥变换器输出电压vAB和vab的基波分量和分别为

BWPT 系统在谐振条件下工作，系统谐振频率ω为

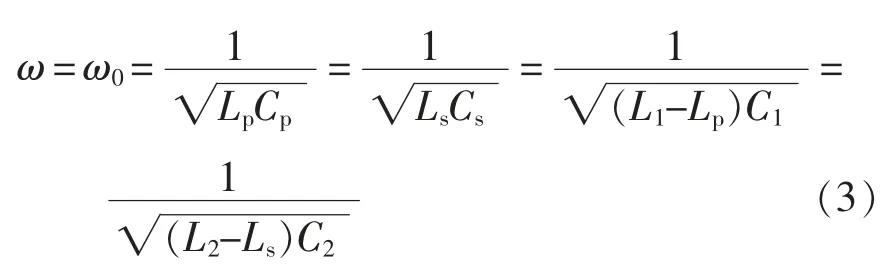
忽略线圈等效电阻影响，由电路理论分析并结合式（1）和式（3）可得，原边输入电流和副边输出电流分别为

在正弦稳态电路中，系统输出有功功率为变换器端口输出电压、电流乘积的实部，输出无功功率为变换器端口输出电压、电流乘积的虚部，并结合式（1）和式（4）可知

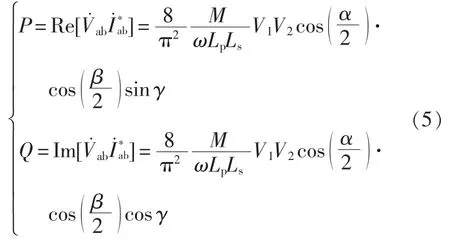
式中：P为变换器端口输出有功功率；Q为变换器端口输出无功功率；为变换器端口输出电流共轭复数。

由式（5）可知，BWPT 系统输出功率大小与α、β、γ 均有关，且功率流的方向主要受影响，控制自由度较多，控制策略比较复杂[15]。

3 BWPT 系统控制策略

根据式（5）有功/无功功率与移相角之间的关系发现，当系统的外移相角γ 被控制在±π/2时，系统输出有功功率最大，此时的无功功率为0，若想控制无功功率为0，则γ 需固定在±π/2，但此时的功率传输方向需要在切换方式下完成。当系统的有功功率发生变化时，γ 会发生变化，进而内移相角也会发生变化，此时的无功功率不再为0。若不控制内移相，即系统的内移相角为0，由无功功率与移相角之间的表达式可以发现，此时无功功率最大，故采用控制内移相角的方法减小系统无功功率。为简化控制策略，且消除功率角切换控制，灵活调节移相角，提高系统传输效率，本文采用了无缝功率环移相控制策略，将原、副边内移相角控制为同一量（即α=β）来控制系统的无功功率，原、副边之间的外移相角γ 用来控制系统的有功功率大小及功率流的方向。其整体控制框图如图4 所示，图中，P为变换器端口输出有功功率参考值，Pab为变换器端口输出有功功率，Q为变换器端口输出无功功率参考值，Qab为变换器端口输出无功功率。

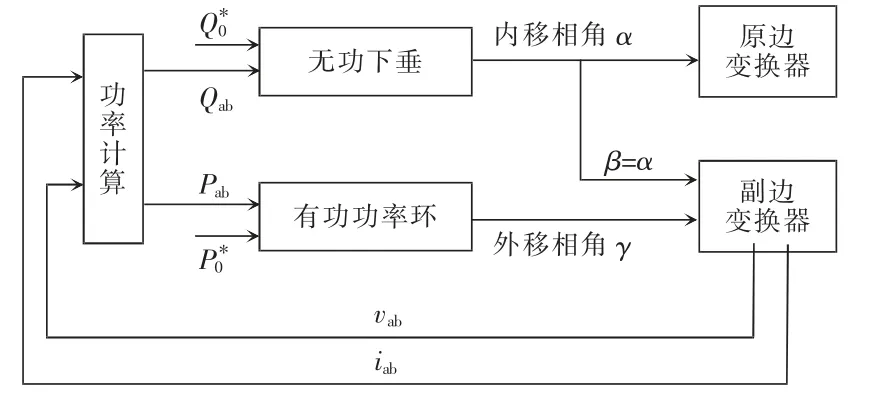
图4 系统整体控制框图Fig.4 Overall control block diagram of system

从图4 中可以看出，通过采集副边变换器交流侧电压/电流，实时计算系统交流侧有功功率和无功功率。系统原边侧和副边侧均采用无功下垂控制结构，减少系统无功功率的产生。同时，副边侧存在有功功率环控制系统输出功率大小及功率流方向，降低了利用切换模式控制系统功率流传输方向对系统稳定性造成的影响。

3.1 原边侧控制策略

为降低变换器交流侧无功功率，原边侧采用无功下垂控制策略控制变换器内移相角α，达到减小回流功率的目的，其控制结构框图如图5 所示。由图5可得，通过采集副边变换器交流侧电压/电流，经功率计算得到交流侧无功功率Qab，根据Qab与其参考值Q 进行无功下垂控制，最终得到控制原边侧PWM的内移相角α。其控制方程为

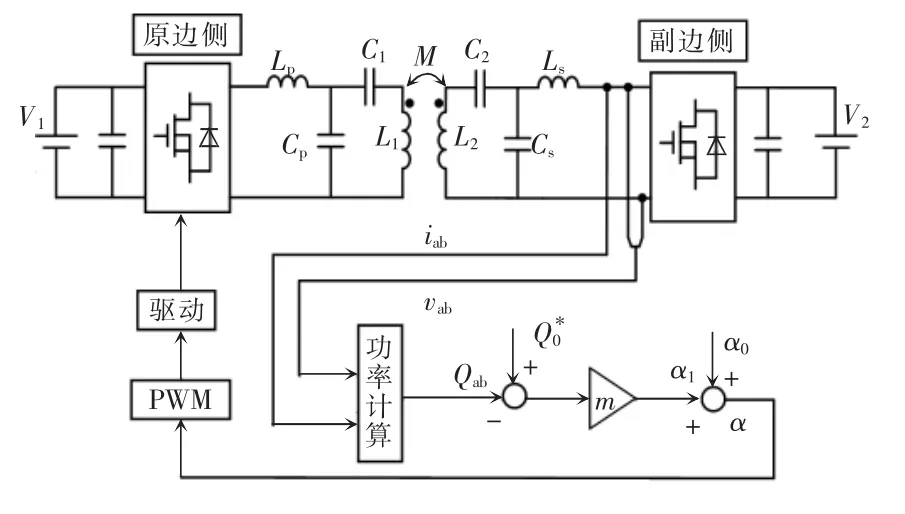
图5 原边侧控制结构框图Fig.5 Block diagram of control structure on primary side

式中：α0为原边内移相角平衡中点值，即直流偏置量；α1为通过下垂控制所得移相角；m为原边无功下垂控制器的下垂系数。

3.2 副边侧控制策略

为了控制BWPT 系统传输功率大小并满足功率双向流动的性能要求，副边侧变换器选取有功功率环控制策略控制原、副边间的外移相角γ。为减小变换器交流侧无功功率的产生，副边同时采用与原边相同的无功下垂控制策略，即副边变换器存在2 个不同的回路协同控制。副边侧控制结构框图如图6 所示。

图6 副边侧控制结构框图Fig.6 Block diagram of control structure on secondary side

由图6 可知，控制副边侧PWM 内移相角α的方法与控制原边侧内移相角的方法相同。通过采集副边变换器交流侧电压/电流，经功率计算得到交流侧有功功率Pab，根据Pab与其参考值P 进行PI闭环控制，最终得到控制原、副边间的外移相角γ。其控制方程为

式中：γ0为原、副边间外移相角的平衡中点值；γ1为通过有功功率环控制所得移相角；G1为副边有功功率环PI 控制器；Kp1和Ks1分别为有功功率环比例和积分控制系数。

4 BWPT 系统仿真

利用Matlab/Simulink 仿真软件搭建双边LCC补偿网络的双向无线电能传输系统拓扑及控制电路仿真模型，双边LCC 谐振补偿网络的参数设计方法及关系见文献[17]，系统仿真所用主要参数设置如表1 所示。

表1 BWPT 系统仿真参数Tab.1 Simulation parameters of BWPT system

图7为系统功率正向传输时，原/副边变换器端口电压、电流仿真波形，由图可知原边变换器端口电压超前于副边90°，实现了功率正向流动。

图7 功率正向传输仿真波形Fig.7 Simulation waveforms in the case of power forward transmission

图8为功率反向流动时，原/副边变换器端口电压、电流仿真波形，由图可知原边变换器端口电压滞后于副边90°，实现了功率反向流动。综上分析，该系统实现了能量双向传输。

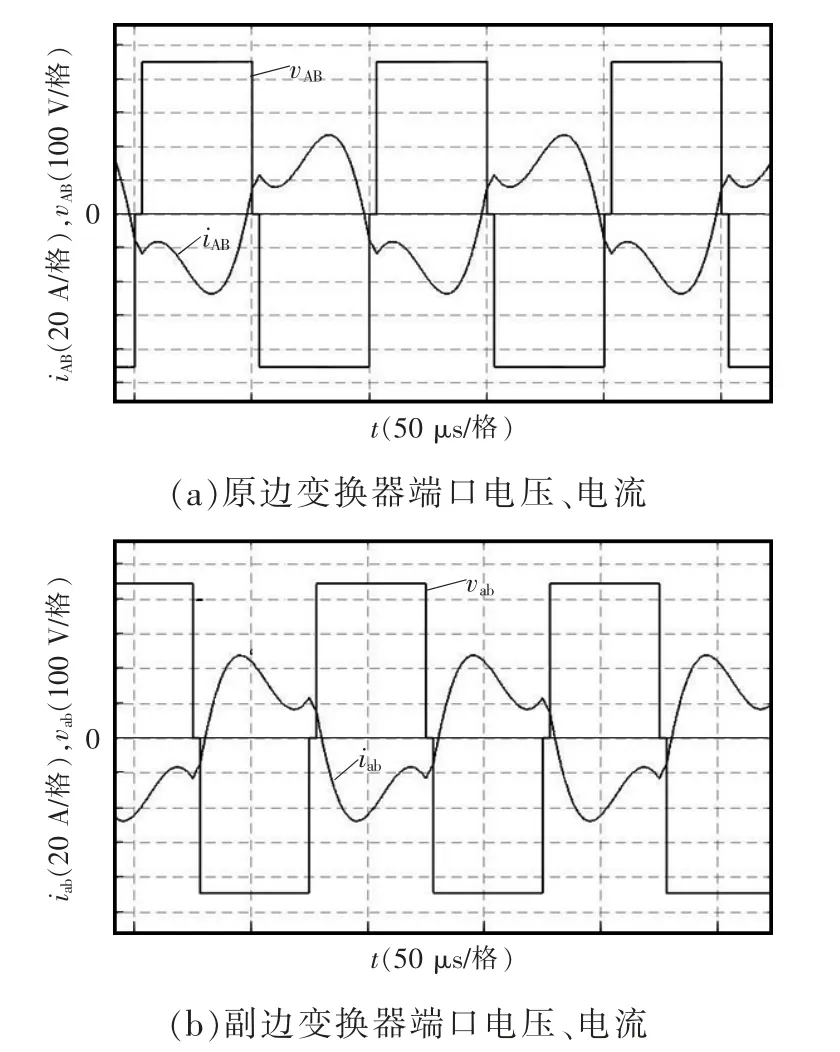
图8 功率反向传输仿真波形Fig.8 Simulation waveforms in the case of power reverse transmission

图9为输出直流电流仿真波形，t1时刻前，输出电流为26.6 A，在t1时刻更改有功功率参考量，输出电流为-26.6 A。

图9 输出直流电流仿真波形Fig.9 Simulation waveform of output DC current

图10为输出有功功率P的仿真波形，t1时刻前，输出有功功率为12 kW，功率正向传输，在t1时刻更改有功功率参考量，输出有功功率为-12 kW，功率反向传输。由仿真结果可知，系统可以通过更改参考量，无需模式切换即可实现功率双向传输。

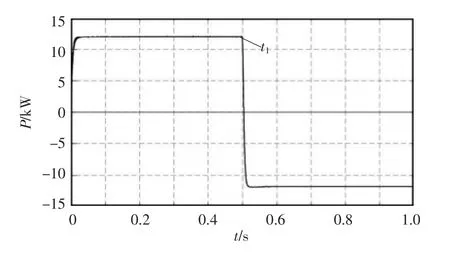
图10 输出有功功率仿真波形Fig.10 Simulation waveform of output active power

图11为传输不同有功时，有无无功下垂控制环路的情况下系统有功-无功关系曲线。由图可知，变换器端口输出无功功率随有功功率的增加而降低；在传输相同有功功率的情况下，有无功下垂控制回路时端口输出的无功功率比无无功下垂控制回路时要小。

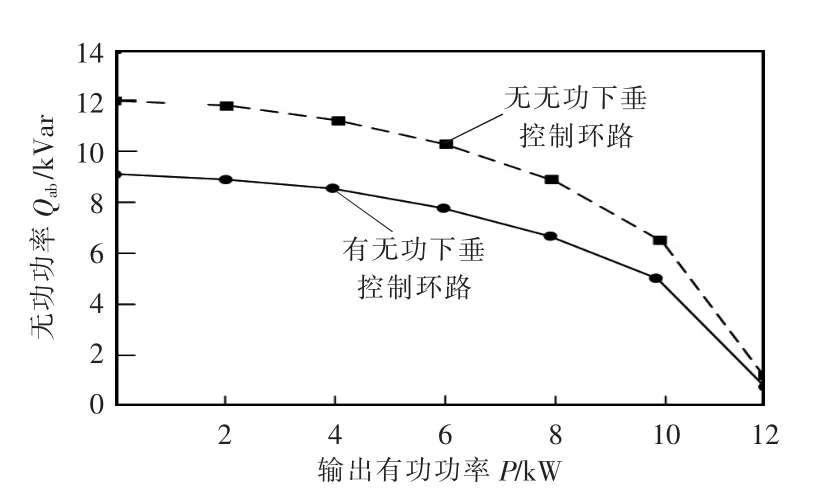
图11 有功-无功功率关系仿真曲线Fig.11 Simulation curves of active-reactive power

由上述分析可知，采用无功下垂控制可以降低系统无功功率的产生，提高系统传输效率。

5 实验验证

为验证所提BWPT 系统无缝功率环移相控制策略可以降低系统无功功率，且无需切换模式即可完成功率双向传输的有效性，利用表1 中的电路参数，搭建半实物实验平台进行实验验证，实验装置如图12 所示，其中原边DSP 控制器实现图5 算法，副边DSP 控制器实现图6 算法。

图12 半实物实验平台Fig.12 Hardware-in-the-loop experimental platform

由于原、副边均有独立的控制器，故需将两边控制信号进行同步，目前通讯部分采用能量/信号并行传输技术[8]，将副边侧的反馈信号经过通讯传输到对应的控制器中。

图13为系统功率正向传输时，原/副边变换器端口电压、电流实验波形，由实验结果可知，电压、电流同向，原边电压超前副边电压90°，实现了功率正向传输。

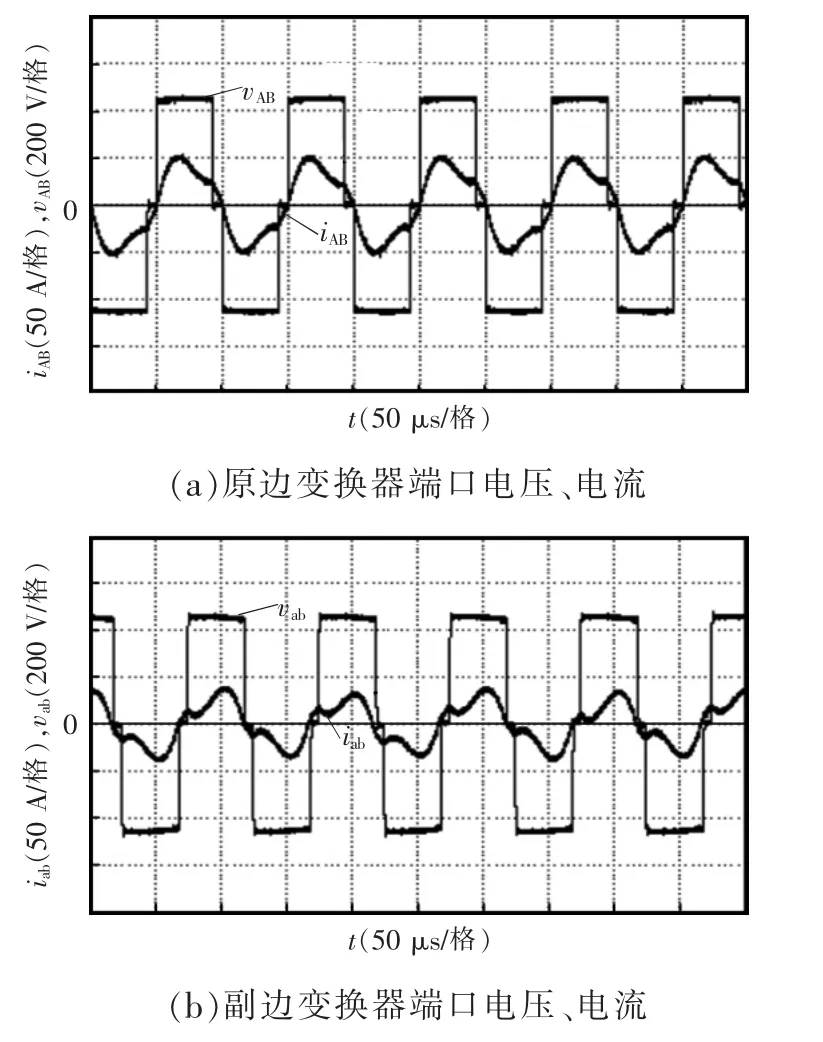
图13 功率正向传输实验波形Fig.13 Experimental waveforms in the case of power forward transmission

图14为系统功率反向传输时，原/副边变换器端口电压、电流实验波形，由实验结果可知，电压、电流反向，原边电压滞后副边电压90°，实现了功率反向传输。上述实验结果与仿真基本一致，实现了功率双向传输。

图14 功率反向传输实验波形Fig.14 Experimental waveforms in the case of power reverse transmission

图15为输出直流电流实验波形，在t1时刻前，输出电流为26.6 A，t1时刻更改系统有功参考指令，输出电流变为-26.6 A。

图15 输出直流电流实验波形Fig.15 Experimental waveform of output DC current

图16为输出有功功率实验波形，在t1时刻前，有功参考指令为正，系统输出有功功率为12 kW，实现了能量正向传输；在t1时刻更改参考指令为负，输出有功功率为-12 kW，实现了能量反向传输。由实验结果可知，采用无缝功率环移相控制实现了无需切换模式即可完成功率双向传输。

图16 输出有功功率实验波形Fig.16 Experimental waveform of output active power

图17为传输不同有功功率时，系统在有无无功下垂控制环路的情况下实验所得系统有功-无功功率关系曲线。由于系统中存在谐波分量，从能量传递的角度出发，该谐波会导致系统存在无功成分[17]。由实验结果可以发现，在传输有功功率相同时，系统加入无功下垂控制环路与未加无功下垂控制环路相比，明显降低了端口输出的无功功率，并且提高了传输效率。

图17 有功-无功功率关系实验曲线Fig.17 Experimental curves of active-reactive power

6 结语

双向无线电能传输系统中谐振网络端口无功功率大、效率低，能量双向传输需要反复切换等问题是BWPT 研究中的热点问题。通过本文提出的无缝功率环移相控制策略可知，采用有功功率环路控制外移相角，无功下垂环路控制内移相角可以实现双向功率无缝切换，且动态响应速度较快。通过对系统有功/无功研究发现，相较于将外移相角控制在±π/2，本文提出的控制方法可以根据不同功率等级和运行状态灵活调节外移相角，提高宽功率范围内的系统传输效率。实验和仿真结果验证了理论分析的正确性，对EV-BWPT 控制策略研究具有一定的参考意义。