一类变指标四阶退化抛物方程解的长时间行为和稳定性

苏彩月,汪颖

(大连交通大学 理学院，辽宁 大连 116021)

近年来，高阶非线性抛物型方程的研究发展日益丰富，主要针对解的存在性、唯一性及解的爆破理论的研究.其中，非线性扩散方程更是一个研究的热点问题,比如相变理论、渗透理论、生物化学等领域都有涉及，特别是退化和奇异的非线性抛物方程,它们在某方面更能反映实际物理意义,如扰动传播的有限性、薄膜方程等.对于这类方程的系统论述Wu等[1]全面介绍了有关退化的非线性扩散方程的基本问题、典型方法以及主要结果等等.本文主要讨论以下四阶变指数退化抛物问题：

(1)

u=Δu=0,x∈∂Ω,t>0

(2)

u(x,0)=u0(x),x∈Ω

(3)

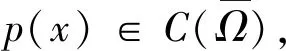
Δ(Δup-2Δu)=λf(x,u)+μg(x,u),x∈Ω

u=Δu=0,x∈Ω

至少有三个弱解的存在性，但关于p-双调和抛物型方程的文献比较少.而本文所讨论的方程类似于发展的p-Laplace方程,有关p-Laplace方程的相关性见文献[3-4].此外，Carrillo和Toscani用熵泛函方法[5]研究了溶液的长时间行为.本文是在郭金勇等[6]研究的基础上进一步研究有关解的长时间行为和稳定性.由于退化,问题(1)～(3)不再具有通常意义下的古典解,因此本文定义如下弱解.

1 主要内容

定理1函数u(x,t)称为问题(1)～(3)的弱解，若其满足以下条件

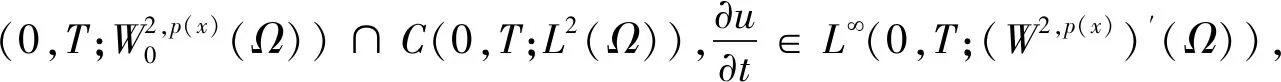
(4)

(3)在L2(Ω)意义下，u(x,0)=u0(x).

定理2设u为满足问题(1)～(3)的弱解(长时间行为)，则有

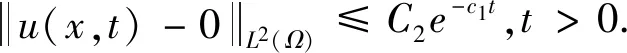
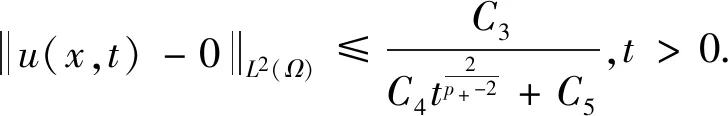
证明 首先选择φ=u作为式(4)的检验函数，有

(5)

于是

(6)

接下来定义熵泛函

很容易得到

(7)

若λ>0,则有

通过求解常微分不等式f′(t)≤-C1f(t)可知

即结论(1)成立.

若λ=0,根据式(7)可知

由于f′≤0,f为递减函数，不妨设f(0)<1,利用嵌入定理可知

因此

即有

定理2证明完成.

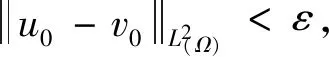
则有

证明 由于u和v是问题(1)～(3)的两个弱解，利用解的定义，可以得到

对固定的s∈[0,T]，取φ=χ[0,s](u-v)作为上式的检验函数，其中χ[0,s]是[0,s]上的特征函数，则

利用事实不等式(|s|p(x)-2s-|t|p(x)-2t)(s-t)≥0,s,t∈R.

设λ≥0可知

即证.

2 结论

本文主要研究了变指标四阶退化抛物方程问题,其存在性采用时间离散化技术，通过构造逼近解，结合能量估计获得一致性估计,进而得到存在性结果.在存在性基础上，利用熵泛函方法，得到解基于熵的能量估计，给出解的长时间行为，进而又获得解的稳定性.