基于CMAC神经网络自整定PID在铁矿品位滴定检测中的应用①

邵 林

(安徽冶金科技职业学院，安徽 马鞍山 243000)

0 引 言

品位是铁矿粉一项重要的技术参数，品位的高低将直接影响选矿的生产成本和生产效率。品位的测量精度对铁矿粉的生产工艺有着重要的指导意义，因此在选矿前必须对铁矿粉的品位进行精确的检测。常用的检测方法有物理研磨法和化学反应法两种，其中物理研磨法是采用打碎研磨和磁选后，通过质量和体积的计算来估计品位的数值。而化学反应法是采用化学试剂参与铁矿反应，最后根据生成物的多少来反推反应物的多少。这两种方法大多数为纯手工检测，效率低，精度难以控制。为了提高检测的效率和检测精度,本文设计了一种基于CMAC神经网络自整定PID加药检测系统，该系统将智能控制理论应用于铁矿粉品位检测中具有非常重要的意义。

1 加药智能检测系统

1.1 硬件装置

加药检测系统由检测试管、小型电加热炉、空气压缩装置、温度传感器、加药滴定装置、信号处理系统等组成。为了便于信息采集和加药滴定，将上述所有装置安装在一个封闭的铁柜中，其中信号处理系统采用西门子PLC来完成。

1.2 工作原理

检测试管盛有适当量的化学比对液，通过比色传感器记录比对液的比色值存入数据库中。再将铁矿粉、反应剂和催化剂放置加热管道内，利用电加热炉将样本加热至适当温度后，向检测管道内吹入压缩空气，将反应的生成物输送至盛有比对液的试管中。由于生成物与比对液相互反应使得比对液颜色发生变化，最后用化学加药的方法将比对液的颜色还原至反应前的比色值，通过计算加药量的多少就可以推出铁矿粉的品位。

2 化学滴定加药仿真模型

滴定加药系统通常采用光电比色计来进行检测，比色计主要通过采集反应溶液的颜色变化值，而在加药过程中反应溶液颜色的变化是非线性且具有大惯性和滞后现象，因此在标准状态下可以用(1)式近似代替滴定加药过程的仿真模型[1]。

(1)

从(1)式可以得出化学滴定加药系统是一个较为复杂的数学模型，如果仅用常规的PID控制方法将难以进行精确的控制。为了满足系统精度要求，将CMAC神经网络与传统PID控制相结合构成自整定控制系统对加药过程进行控制。通过CMAC自整定PID动态调整控制参数，从而使加药系统的动态、静态性能都达到较好的效果，基本满足铁矿品位的计算精度要求。

3 CMAC自整定PID控制算法

3.1 CMAC自整定PID原理图

本文设计的CMAC自整定PID控制算法的原理如图1所示，神经网络的输入为e，输出为PID的kp、ki、kd三个参数[2]。

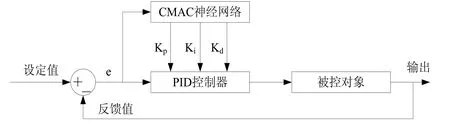
图1 CMAC自整定PID控制原理图

3.2 神经网络

CMAC自整定PID算法采用CMAC神经网络和传统PID相结合。众所周知，CMAC神经网络是前馈控制模式，输入与输出由概念映射和实际映射两个基本映射来完成。设输入向量为up=[u1p,u2p,...,unp]T，量化编码为[up]，输入映射至AC中c个存储单元(c为二进制非零单元数目)，采用下式映射后的向量[3]：

Rp=S([up])=[S1(up),S2(up),...,Sc(up)]T

式中，

sj([up])=1,j=1,2,...,c

(2)

若只考虑单输出，则输出为：

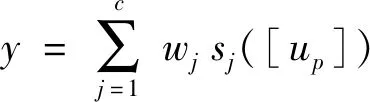
其中，

wj=[w1,w2,...,wc]T

(3)

CMAC神经网络学习算法采用δ学习规则调整权值，权值调整指标为：

wj(t)=wj(t-1)+Δwj(t)+

α(wj(t-1)-wj(t-2))

(4)

wj=[w1,w2,...,wc]T，式中，α为惯性系数，η为学习速率。

3.3 权值的调整

系统通过CMAC神经网络自整定PID的三个参数，根据各自在调节过程中的作用，对学习算法作出如下改进：

由梯度下降法，I、P、D三个参数的输出权值分别按照按下式调整[4]：

(5)

式中，ηI为I的学习速率，αI为I的惯性系数。

(6)

式中，ηP为P的学习速率，αP为P的惯性系数 。

(7)

式中，ηD为D的学习速率，αD为D的惯性系数。

4 控制算法的仿真研究

4.1 阶跃响应分析

设置输入rin(k)=2，仿真曲线如图2所示。a曲线为CMAC自整定PID算法，b曲线为传统PID控制算法。由仿真曲线可知传统PID控制算法超调量近似为25%，调节时间近似为7s，适当调节PID的三个参数，可以改变超调量的大小，但是调节时间也会加大，不能满足系统的控制要求；而智能自整PID控制算法超调量仅为5%，系统调节时间减少到仅为2s。

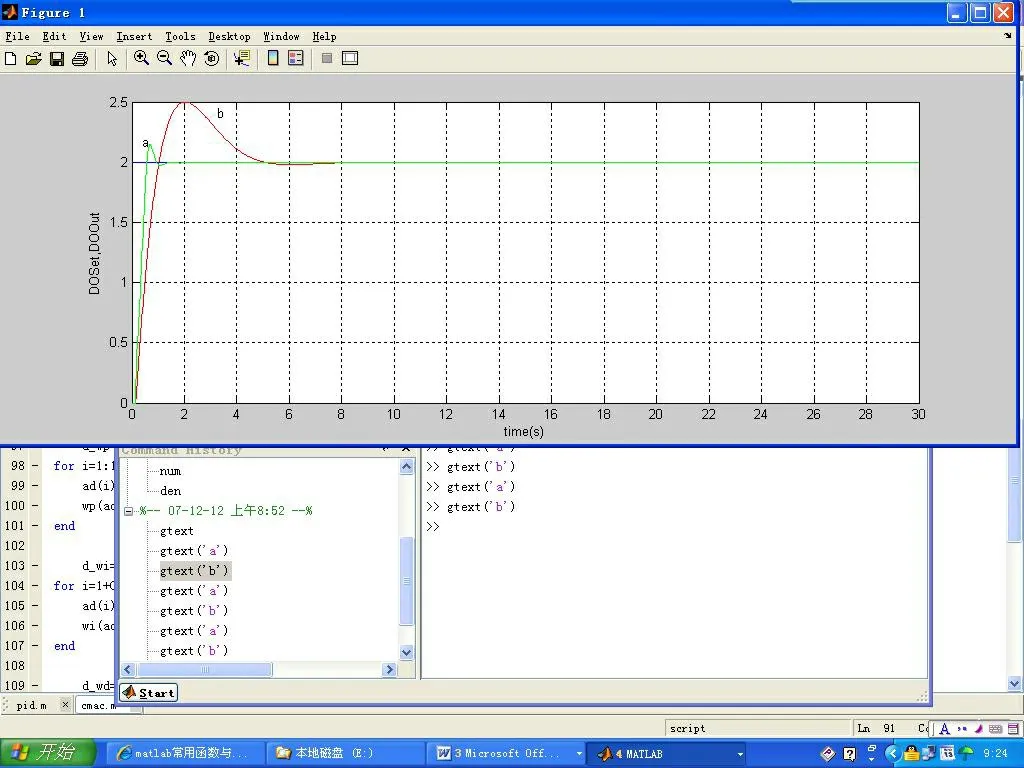
图2 阶跃响应仿真曲线

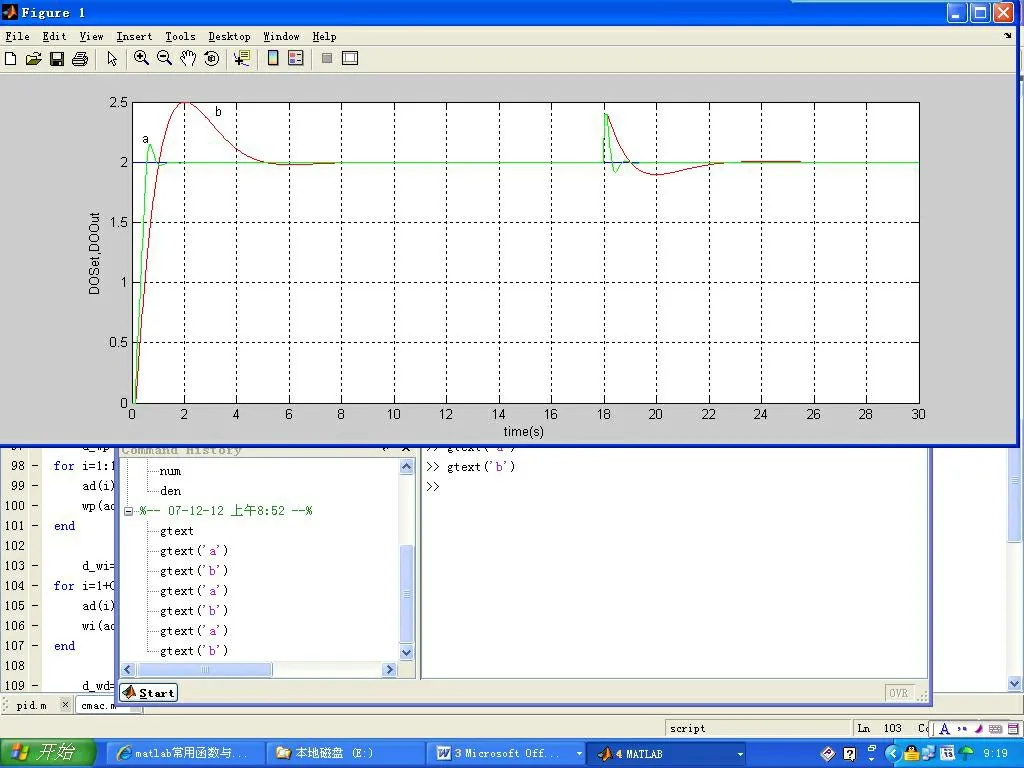
图3 抗干扰性仿真曲线

4.2 抗干扰分析

在20s的时刻系统的输出端加入0.5的干扰信号，仿真结果如图3所示，a是采用CMAC神经网络自整定PID控制算法的抗干扰仿真曲线，b是采用普通PID控制的抗干扰仿真曲线。当加入扰动信号后，两种控制算法的仿真曲线均发生振荡，CMAC自整定PID控制算法加入干扰后仅过1.6s就进入稳态，而采用普通PID控制算法系统加入干扰后经过8s才进入稳态。通过分析，两种算法产生的超调量基本相同，但从调节时间来看CMAC自整定PID控制算法要小于普通PID控制，因此CMAC神经网络自整定PID控制算法抗干扰性能更好。

4.3 鲁棒性分析

4.3.1 稳态增益Kc

将系统稳态增益由950变为650，仿真曲线如图4所示。其中曲线a为CMAC自整定PID控制算法增益为950的仿真曲线；曲线a1为CMAC自整定PID控制算法增益为650的仿真曲线；曲线b为普通PID控制算法增益为950时的仿真曲线；曲线b1为普通PID控制算法增益为650时的仿真曲线。由上述仿真可以得出稳态增益改变时CMAC自整定PID控制算法超调量增加了5%，调节时间没有大的变化；普通PID控制算法超调量增加了5%且调节时间增大近一倍为12s。因此CMAC自整定PID控制策略较普通PID控制鲁棒性更好。

4.3.2 惯性时间常数Tc

将惯性时间常数Tc由65调节为90，仿真曲线如图5所示。其中仿真曲线a和a1分别为采用CMAC自整定PID控制算法时间常数为65和90时的仿真曲线；而仿真曲线b和b1分部为传统PID算法当时间常数为65和90时的仿真；由图4和图5分析可知，当时间常数Tc改变时，CMAC自整定PID控制算法的超调量增加了3%，但相对调节时间基本没变；而传统PID控制算法超调量增加5%且调节时间增大至12s，从以上仿真分析可以得出：CMAC自整定PID控制算法在鲁棒性方面更优于较传统PID控制算法。

图4 鲁棒性仿真曲线

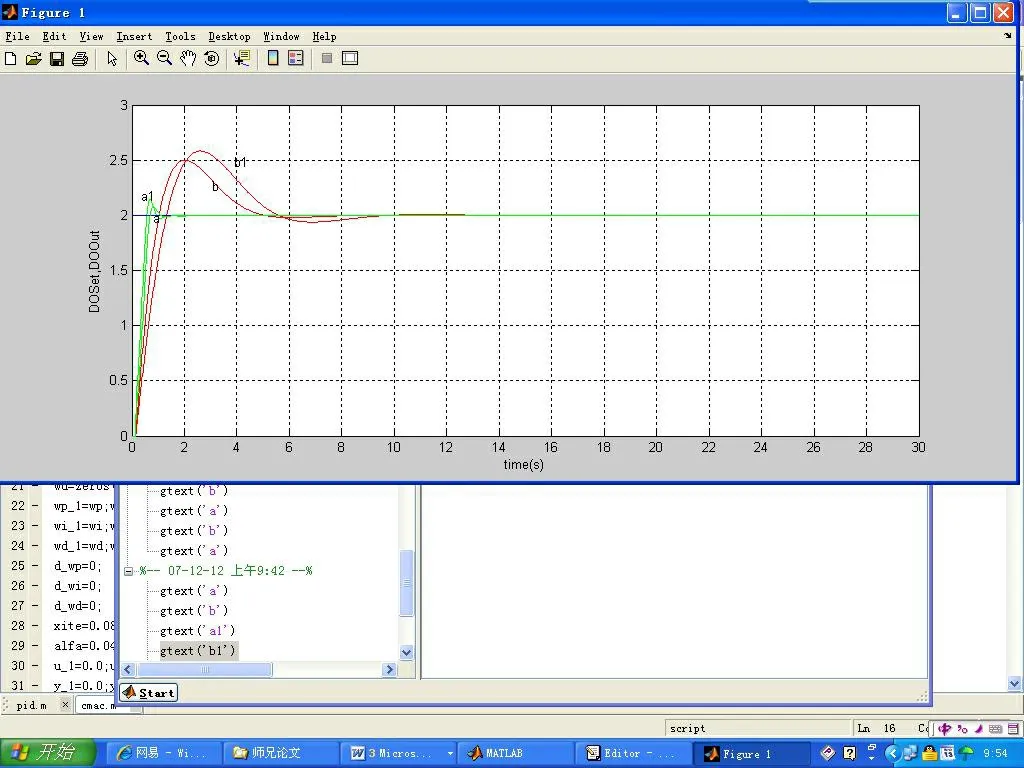
图5 鲁棒性仿真曲线

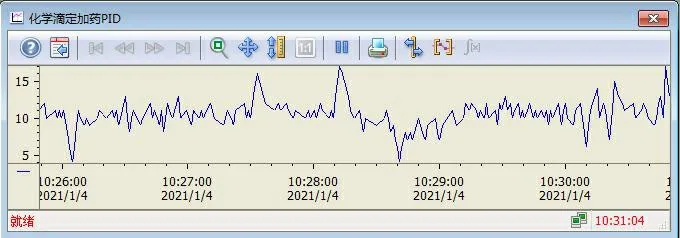
图6 传统PID变化趋势图

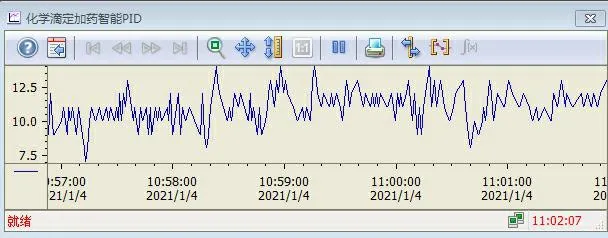
图7 智能PID变化趋势图

5 比色计采样

5.1 采样方法

在加药滴定检测前，首先将比色计模拟信号通过接口电路传输至西门子S7200 Smart PLC的模拟量模块中，PLC通过DB数据块存入比色计原始信号。开始检测时，将铁矿粉加热后，通过压缩空气将铁矿粉中的有效物质吹入比色计试管中进行反应，此时比色计的信号将连续变化，直至样本全部反应完成后，比色计的信号保持不变。

5.2 反处理方法

反向加药反应，比色计颜色逐渐还原，PLC连续监控比色计的变化数值，当比色计的数值被还原至原始数值时，立即停止向试管中加药，此时记录参加反应的还原剂的质量。最后根据样本的质量和还原剂的质量进行化学计算可以较为精确地得出样本的品位值。

5.3 采样分析

为了比较本文设计的CMAC自整定PID和普通PID控制算法的性能，分别在化学滴定加药过程中对比色计的信号进行控制。文中采用上位机软件WinCC进行信息收集和分析，分析变化趋势图如图6和图7所示。在滴定加药过程中，由趋势图6可知传统PID控制算法超调量且变化较大，图7显示表明CMAC神经网络自整定PID控制算法具有良好的动态性能且可以在线调整，大大的提高算法的自适应能力。

6 结 论

通过Matlab对两个系统分别从阶跃响应、抗干扰和鲁棒性进行仿真分析，以及对加药滴定检测系统的趋势图分析，可以得出本文设计的基于CMAC神经网络自整定PID控制算法较好地解决了化学加药滴定系统被控对象大惯性的问题，有效地提高了控制系统的控制精度，基本能够满足化学滴定加药控制的要求。同时采用西门子PLC进行数据采集，可以提高系统运行的自动化程度。采用上位机软件能够快速地进行数据分析和存储，便于样本数据的比对和输出，有效地提高了检测的速度和效率。