康复机械手运动学旋量逆解及算法验证①

朱 磊， 许德章,*

(1.安徽工程大学人工智能学院,安徽 芜湖 241000；2.芜湖安普机器人产业技术研究院,安徽 芜湖 241007)

0 引 言

传统串联机器人通常采用 D-H 参数法[1]和旋量法[2]建立机器人的运动学模型。D-H 参数法需要在每个关节处建立局部坐标系，用4个参数的变换矩阵表示不同坐标系之间的变换，以此描述坐标系间的变化规律。当使用D-H参数法对相邻关节平行的机器人建立局部坐标系时，会带来参数奇异性的问题，与之相比，旋量法使用工具坐标系和基坐标系来描述刚体的整体运动，运动参数的变化更加光滑，避免了建立局部坐标系带来的奇异性问题，物理意义更加明确。赵荣波[3]等基于旋量理论，采用代数和Paden-Kahan子问题相结合的方法对末端3个关节交于一点的6R机器人进行了逆运动学求解，方法上具有一定的优越性；Wang[4]等基于3种基础Paden-Kahan子问题，提出了几种新型逆运动学子问题，为机器人的逆运动学求解提供了新思路。考虑到康复机械手具有3个轴线相互平行的相邻关节，因此采用旋量法与代数相结合的方法对其逆运动学问题进行求解，之后从人手的基本运动功能出发，提出两种抓握手势作为算法正确性验证的评价指标，使用MATLAB和Robotics Toolbox验证方法的正确性，为康复机械手的逆运动学求解提供了思路。

1 理论基础

(1)

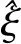
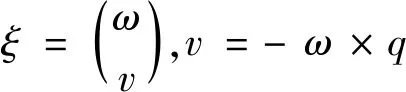
(2)

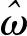
(3)

则刚体运动用矩阵指数的形式表示为

(4)

(5)

用S表示基坐标系，T表示末端坐标系，则单个关节的初始位姿gst(0)与末端位姿gst(θ)的关系表示为

(6)

推广到n关节的康复机械手中，则康复机械手的末端姿态与初始位姿间的关系用指数积的形式表示为

(7)

2 康复机械手逆运动学算法建立

2.1 运动学建模

康复机械手在结构上与人手相似，是由拇指、食指、中指、环指、小指以及掌部和腕部组成，各个手指都拥有4个自由度，在与人手绑定后，通过自身的运动实现对人手的助力与康复训练。其上的运动包括腕掌关节的摆动和弯曲以及近端指节和远端指节的弯曲运动，其中，摆动轴与弯曲轴相互垂直。其余四指在结构上相同，与掌部相连，其运动可分为掌指关节的摆动和弯曲，以及近端指节和远端指节的弯曲运动。

将拇指的基坐标系设在腕掌关节处，将其余四指的基坐标系设在掌指关节处，则康复机械手的手指的运动模型可以用图1表示。

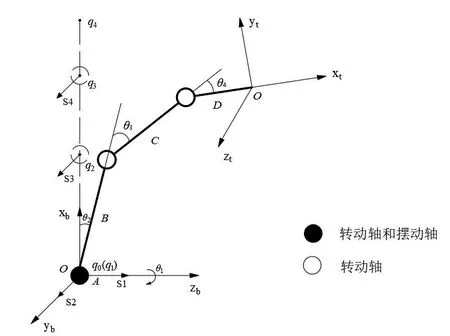
图1 手指运动模型

由图1可以得出机械手关节转动轴上的一点qi以及轴线方向矢量ωi分别为

q1=(0 0 0)T，q2=(A0 0)T，

q3=(A+B0 0)T，q4=(A+B+C0 0)T

(8)

ω1=(0 0 1)T，ω2=(0 1 0)T

ω3=(0 1 0)T，ω4=(0 1 0)T

(9)

末端执行器的初始位姿gst(0)为

(10)

(11)

由旋量理论得康复机械手的手指正运动学映射为

(12)

经过计算与化简可得

(13)

式(13)中，ci=cosθi，si=sinθi，i=1,2,3,4；c23=cos(θ2+θ3)，s23=sin(θ2+θ3)，

c234=cos(θ2+θ3+θ4)，s234=sin(θ2+θ3+θ4)，px=c1(A+Bc2+Cc23+Dc234)，py=s1(A+Bc2+Cc23+Dc234)，pz=-(Bs2+Cs23+Ds234)。

2.2 逆运动学求解

2.2.1 求解θ1

因为轴S2,S3,S4相互平行，在姿态变换中，可将运动旋量ξ2,ξ3,ξ4看作是一个整体，则运动旋量ξ1,ξ2,ξ3,ξ4所表示的基坐标系到工具坐标系的姿态变化可用Z-Y-X欧拉角表示，即

Rzyx(θ1,θ234,0)=Rz(θ1)Ry(θ234)Rx(0)=

(14)

在式(12)的两侧同时右乘gst(0)-1，并令g=gst(θ)gst(0)-1，则有

(15)

采用对应元素相等的方法，利用Rzyx(θ1,θ234,0)与g中第二行第二列的元素相等可得

θ1=arccos[g(2,2)]

(16)

式(16)中，g(2,2)表示g的第二行第二列元素。

2.2.2 求解θ3

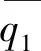
(17)

此时式(15)可改写成

(18)

(19)

则点q4到g′的距离可以表示为

(20)

(21)

式(21)表示将点q1绕轴S3旋转至与点q4相距g′处，因而可使用第3类Paden-Kahan子问题[5]求解θ3。于是有

(22)

式(22)中，u3=(q1-q3)-ω3ω3T(q1-q3)，w3=(q4-q3)-ω3ω3T(q4-q3)，δ32=g″2-|ω3T(q1-q4)|2，θ′=arctan2(ω3T(u3×w3),u3Tw3)。

2.2.3 求解θ4

因为DIP关节与PIP关节之间相互耦合，参照HandeXos-gamma外骨骼康复手[6]，则DIP关节与PIP关节间的耦合系数为1，于是有

θ4=θ3

(23)

2.2.4 求解θ2

(24)

(25)

(26)

(27)

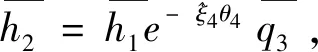
(28)

θ2=arctan2(ω2T(u2×w2),u2Tw2)

(29)

式(29)中，u2=(q3-q2)-ω2ω2T(q3-q2)，w2=(h2-q2)-ω2ω2T(h2-q2)。

3 逆运动学算法验证

3.1 两种验证手势

抓握是人手活动中最基础的功能，考虑到脑卒中患者手部的病态蜷曲多数是由屈肌与伸肌作用不平衡导致的[7]，因此康复机械手的首要功能是训练患者手部在矢状面进行屈伸运动，结合Ian M.Bullock[8]对人手抓握姿态的研究，得到两种使用频率最高的抓握手势，即掌握(图2左)和指腹捏(图2右)。验证逆运动学算法的正确性。

根据Arbib[9]对虚拟手指(Virtual Finger)的定义，将掌握归为掌面对抗(palm opposition)，其中手掌作为VF1，食指、中指、环指、小指作为一个功能单元用VF2表示；将指腹捏归为指面对抗(pad opposition)，其中拇指作为VF1，其余四指作为VF2，得出两种抓握手势的对抗模型如图3所示。

3.2 实例验证

HandeXos-gamma外骨骼康复手满足所述康复机械手的构型要求，因此选择其结构参数验证算法的正确性，由对抗模型可知，除拇指外其余四指都作为一个功能单元(VF)，所以仅给出拇指和食指的参数，具体参数如表1所示。

图2 两种基础抓握手势

图3 两种抓握动作下手的对抗模型

表1 康复机械手各关节长度

在人手关节的活动范围内，给出上文两种手势中各关节角度，如表2所示，其中θ1与θ2分别表示关节的伸展和屈伸(拇指中为CM关节，其余四指中为MP关节)，θ3与θ4分别表示PIP关节和DIP关节的伸展。

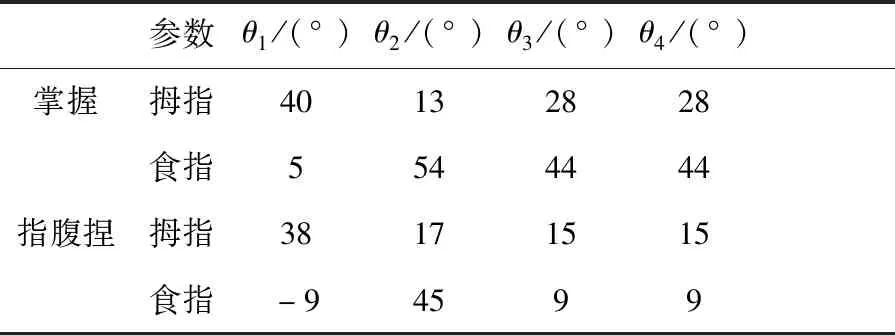
表2 两种手势下的理论关节角度

具体验证过程如下。

(1)由所给参数应用正运动学方程得到康复机械手的末端位姿。

(2)利用所提出的逆运动学算法，求解在两种手势下拇指和食指的各关节角度，舍弃掉在人手关节活动范围之外的解。

(3)使用MATLABRoboticsToolbox处理所得结果得到指关节的位姿图。

(4)比较逆运动学算法得到的关节角度解与所给出的关节角度间的误差，若误差在许用范围之内，则验证所提算法正确；否则所提算法不正确。

按照上述步骤使用MATLABR2018a软件计算两种手势下拇指与食指的逆运动学解如表3所示，关节位姿如图4所示。

表3 两种手势下的实际关节角度

图4 两种手势下的实际手指位姿

比较理论关节角度和实际关节角度的值，得到关节角度误差。其中最大误差发生在掌握手势中食指MP关节的伸展，其值为Δθmax=-0.1301° 。因为该误差对人手康复运动影响极小，因此可认为所提出的康复机械手逆运动学算法在理论上可行。

4 结 论

建立康复机械手的结构模型，采用旋量法建立康复机械手的运动学方程，使用旋量与代数相结合的方法和Paden-Kahan子问题求解手指的逆解，具有明确的几何意义，并以人手的抓握功能为基础提出了两种抓握方式，在此基础上通过实例验证了逆运动学算法的有效性和康复机械手在结构上的可行性。