反应性RM不稳定混合特性研究：反应活性与介质不均匀性的影响

汪 洋， 董 刚

(南京理工大学瞬态物理重点实验室， 江苏南京 210094)

引 言

当激波与带扰动的界面作用时， 界面形成的密度梯度和激波形成的压力梯度方向不一致导致界面涡量沉积， 使得扰动增长， 后期这种失稳会促进界面两侧流体发生湍流混合， 这种现象被称作Richtmyer-Meshkov(RM)不稳定性。RM不稳定现象在航空发动机超燃混合[1]、 惯性约束聚变[2-3]、 工业爆炸灾害[4]中都有所涉及， 当界面本身或者界面两侧介质之间可以发生化学反应时， RM不稳定过程会变得更为复杂， 相关研究开展得并不充分。因此， 相关的激波诱导火焰失稳、 燃烧和混合特性的研究具有重要意义。

关于惰性界面在激波作用下的扰动增长和混合特性研究目前已经得到了较为充分的发展， 国内外已经开展了大量的理论、 实验和数值模拟研究。翟志刚等[5]和Luo等[6]开展了一系列激波冲击惰性界面的RM不稳定实验研究， 考察了扰动模式等因素对界面发展的影响， 并对界面扰动的线性与非线性增长进行理论分析和预测。蒋华等[7-8]对激波诱导惰性扰动界面的RM不稳定增长过程进行了二维数值研究， 分析了初始扰动条件对反射激波前后界面扰动增长的影响。

与惰性RM不稳定性的研究相比， 反应性RM不稳定的研究较少且主要集中于数值模拟研究。Khokhlov等[9]采用二维带化学反应N-S方程， 数值研究了单次激波与单模扰动预混火焰界面的相互作用过程， 发现RM不稳定所导致的火焰面积增加以及激波压缩带来的介质密度增加可促进燃烧放热率。Massa等[10]在研究激波单次作用下预混火焰界面的失稳机制过程中， 发现火焰界面的增长速度明显受到化学反应的影响， 并且化学反应会减少火焰表面的小尺度扰动。Jiang等[11]采用带单步化学反应的N-S方程对激波及反射激波与预混火焰界面的多次作用的二维和三维过程进行系列研究， 考察了界面扰动模式、 入射激波强度等因素对反应性RM不稳定过程的影响， 发现化学反应在一定程度上可以抑制大尺度流动带来的界面混合效应。

目前已有的反应性RM不稳定研究更多地集中于均匀介质的情况， 实际中预混气体往往是非均匀的， 气体的非均匀性一方面会导致流体介质的不均匀性， 另一方面也会导致反应活性发生变化(例如通过改变预混气体的当量比)， 而这种不均匀性会对RM不稳定带来哪些影响， 目前尚未得到充分研究。本文基于带单步化学反应的二维N-S方程， 采用高精度计算格式， 数值研究了入射激波及其反射激波与预混火焰界面的相互作用过程， 主要考察了在不同化学反应活性以及介质不均匀的条件下， 反应性RM不稳定界面混合特性的变化规律。

1 数值方法

1.1 控制方程及计算方法

本文数值模拟采用了基于单步化学反应的二维N-S方程， 如下所示

(1)

其中

U=(ρ,ρu,ρv,ρe,ρY)T

F=(ρu,ρu2+p,ρuv, (p+ρe)u,ρYu)T

G=(ρv,ρvu,ρv2+p, (p+ρe)v,ρYv)T

FD=(0,τxx,τxy,qx+uτxx+vτxy,D∂(ρY)/∂x)T

GD=(0,τyx,τyy,qy+uτyx+vτyy,D∂(ρY)/∂y)T

式中，F，G为对流通量项；FD，GD为输运通量项；ρ为密度；u，v分别是x，y方向上的速度分量；p为压强；e为单位质量的总能量， 假设气体为量热完全气体， 则e可定义为

e=p(γ-1)/ρ+0.5(u2+v2)+qY

式中，γ为绝热指数，q为单位质量化学反应放热，Y为反应物质量分数。qx，qy为热通量，qx=-k∂T/∂x和qy=-k∂T/∂y。T为温度，τij(i=x，y；j=x，y)为黏性应力张量分量， 表达为

其中，δij为Kronecker函数。以上各式中输运系数， 如导热系数k、 扩散系数D、 运动黏性υ， 三者与温度的关系表达为[4]

式中，n取0.7， 本文假设Lewis数、 Prandtl数、 Schmidt数均设定为1， 因此，k0，D0，υ0为相等的常数为k0=D0=υ0=3.2×10-7kg/(s·m·K0.7)， 对于化学反应， 本文采用了单步Arrhenius反应模型， 化学反应速率的表达式为

其中，A为指前因子， 取A=1.2×108m3/(kg·s)，Ea为化学反应活化能，R为通用气体常数。

计算中采用分裂算法求解方程(1)， 其中对流通量项采用LF(Lax-Friedrichs)格式结合9阶WENO[12]模板进行求解， 输运通量项采用10阶中心差分格式进行求解， 化学反应源项和时间导数项采用3阶Runge-Kutta法求解， 上述方程及计算方法在以前的研究[7,8,11,13-14]中得到广泛应用。

1.2 初始条件及边界条件

本文中的反应性RM不稳定过程中， 采用了平面激波与带扰动的反应性界面相互作用的方式研究不同反应活性的影响， 这里的二维界面形态可以表达为

a(x)=a0[cos(2πx/λ0)]

(2)

其中，a0为界面的初始扰动振幅，λ0为初始界面扰动波长。

另一方面， 为考察介质不均匀性对反应性RM不稳定界面混合特性的影响， 采用了平面激波与带有初始密度分布的流场所形成的界面相互作用的方式， 其中界面两侧的密度沿x方向的分布表示为

其中， 下标1和2分别代表预混火焰界面的未燃侧和已燃侧， 未燃气侧的平均密度ρ1=0.161 5 kg/m3， 已燃气侧的平均密度ρ2=0.015 78 kg/m3，σ代表了密度分均匀分布的幅值， 其取值范围为0<σ<1， 当σ>0时， 平面入射激波在运动时会由于密度的不同逐渐形成正弦型曲面激波， 这种激波与平直界面相互作用时， 亦会由斜压效应而产生RM不稳定。本文取σ=0.35以保证曲面激波刚通过平直界面时， RM不稳定导致的界面产生的振幅与式(2)中的初始扰动振幅a0基本相同。以上两种激波与预混火焰界面相互作用的计算构型如图1(a)， (b)所示,非均匀流场(图1(b))中密度沿x方向的分布如图2所示。

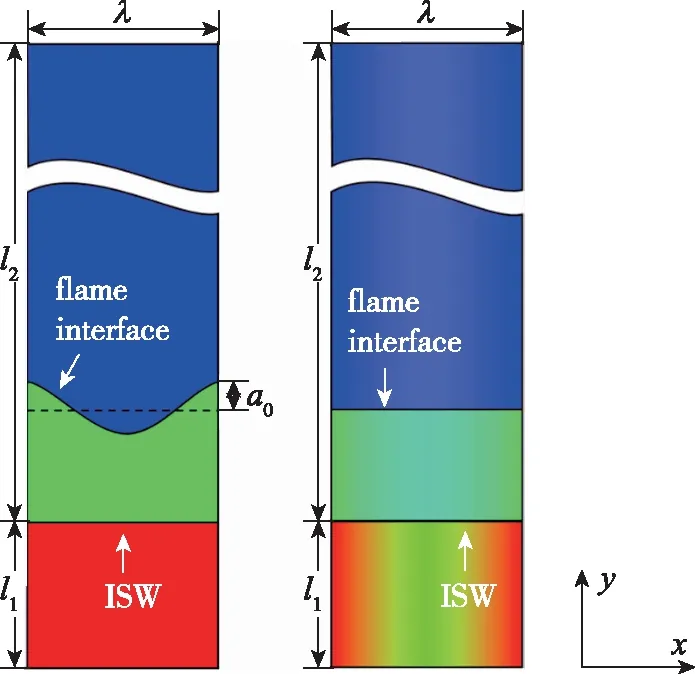
(a) Sinusoidal flameinterface (b) Planar flame interface图1 预混火焰界面初始形态(ISW为入射激波)Fig. 1 Initial patterns of premixed flame interface(ISW is incident shock wave)

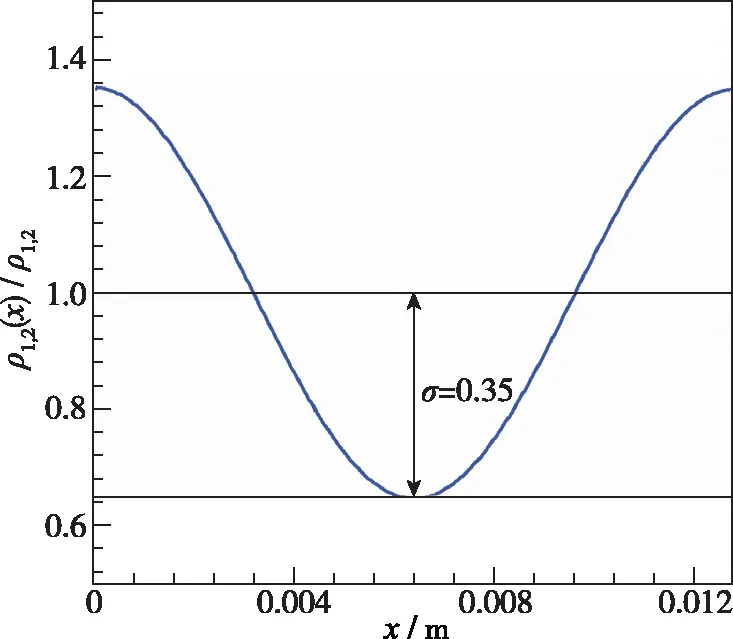
图2 非均匀流场中密度沿x方向的分布Fig. 2 Distribution of density along the x direction in inhomogeneous flow

图1中， 火焰界面下方为未燃预混气体， 其初始压力和初始温度分别为p0=13.3 kPa和T0=293 K， 界面上方为已燃气体， 其热力学特征根据等压燃烧过程计算得到， 界面两侧的Atwood数为At=(ρ2-ρ1)(ρ2+ρ1)=-0.822。

为考察介质反应活性和介质均匀性的影响， 选择了不同反应活化能Ea和不同σ开展计算， 计算参数的设置如表1所示。

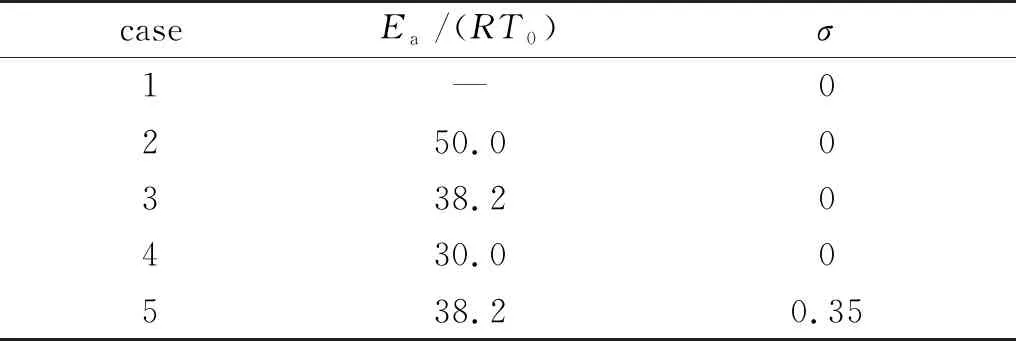
表1 计算参数

表1中算例1代表了均匀介质中平面激波与冻结流界面的相互作用， 该算例的目的是和反应流的结果进行对比；算例2～4代表了均匀介质中平面激波与反应性界面的相互作用；而算例5则代表了非均匀介质中激波与界面的相互作用情况。

在表1的所有算例中， 计算域均采用x×y=0.012 8 m×0.6 m的矩形区域， 其左右边界(沿x方向)为周期边界条件， 下边界为零梯度边界条件， 上边界为绝热刚性无滑移边界条件。为考察计算的精度， 本文首先针对算例3开展了网格无关性测试， 图3给出了3种不同网格尺寸下混合区宽度随时间的变化对比。

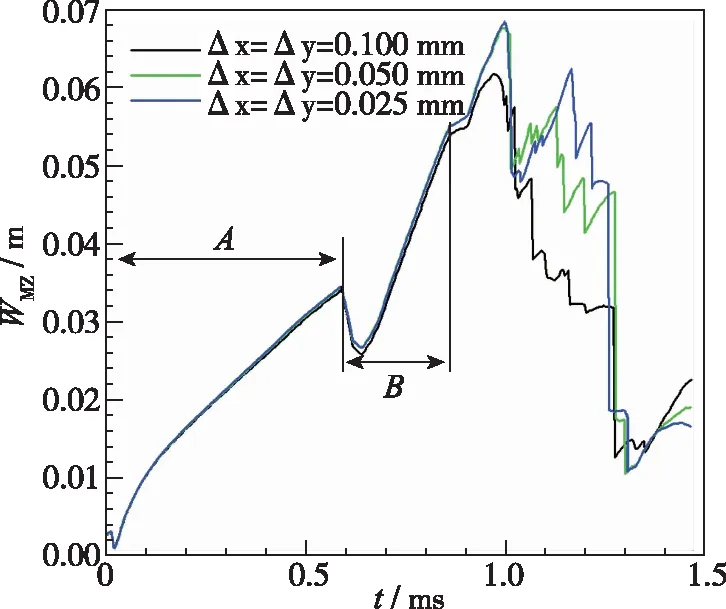
图3 不同网格尺寸下混合区宽度随时间的变化Fig. 3 Time histories of width of mixing zone with different grid resolutions

图中A，B两个阶段分别为入射激波和第一次反射激波作用后混合区宽度的变化阶段， 阶段B的初期存在一个混合区宽度下降过程， 这是反射激波作用于火焰界面时对界面的压缩导致的。以上结果表明在阶段A和阶段B中， 3种网格尺寸计算的结果相互吻合较好， 但在阶段B之后的反射激波与火焰界面相互作用的过程中， Δx=Δy=0.1 mm尺寸下的计算结果要明显低于Δx=Δy=0.05 mm和0.025 mm尺寸下的计算结果， 这表明火焰界面失稳是向着小尺度结构的方向发展的， 因此， 本文研究仅考虑阶段A和B的相互作用过程， 采用Δx=Δy=0.05 mm的网格尺寸进行数值模拟， 每一个算例总网格数约为3.072×106， 为提高计算效率采用了基于MPI并行策略进行编程计算。

2 结果与讨论

2.1 火焰界面演化特性

为了考察化学反应活性对界面混合特性的影响， 图4(a)～(c)分别给出了不同反应活性下若干典型时刻的预混火焰界面演化形态， 这些典型时刻分别代表入射激波作用后界面发展前期 (t=0.2 ms)和后期 (t=0.5 ms)， 以及反射激波作用后(t=0.8 ms)的某些时刻。

在t=0.2 ms时， 4种条件下的火焰界面形态均呈现出“钉-帽-泡”结构， 其主要差异在于钉结构的两侧所呈现的涡结构， 随着化学反应活性的增强(Ea=30.0RT0)， 涡结构内反应物几乎完全消耗， 其原因主要是由于RM不稳定过程中形成的涡结构促进了界面两侧已燃气和未燃气的混合， 从而加速了反应物的消耗。当t=0.5 ms时， 可以看到4种条件下， 界面上方的“钉”结构继续向上发展， 界面下方的“泡”结构向下发展， “帽-涡”结构差异较大， 当反应活性最强(Ea=30.0RT0)时， “帽”结构以及“钉”两侧的涡结构已经被化学反应所消耗， 这也导致其反应区宽度出现突然下降(见图4(b))。

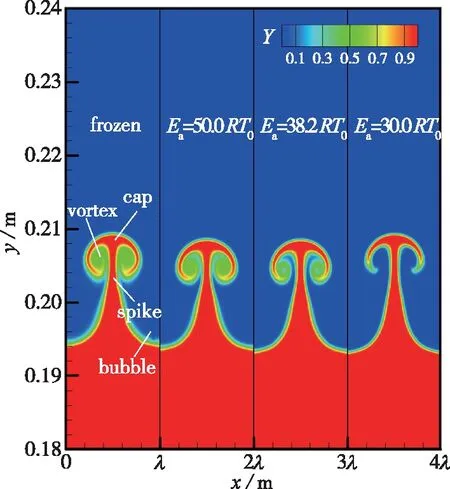
(a) t=0.2 ms

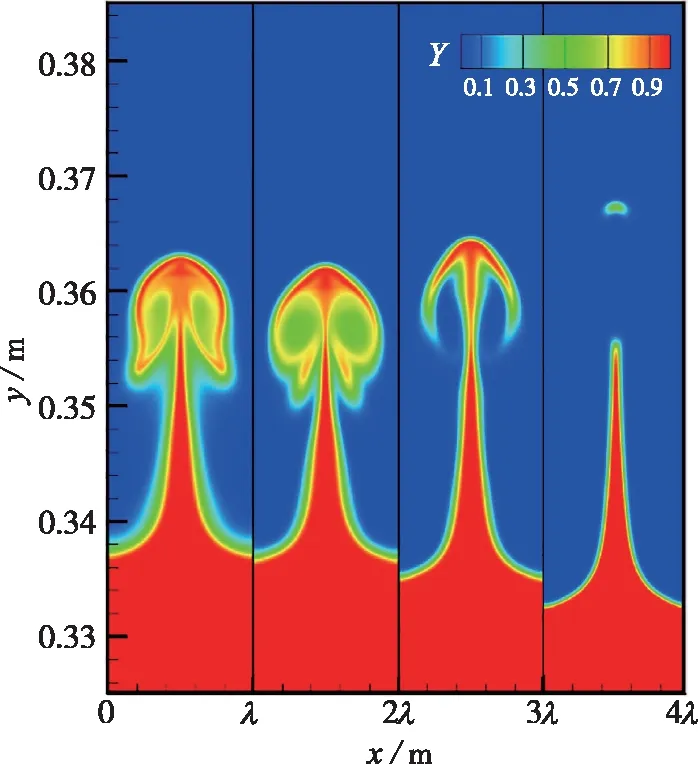
(b) t=0.5 ms

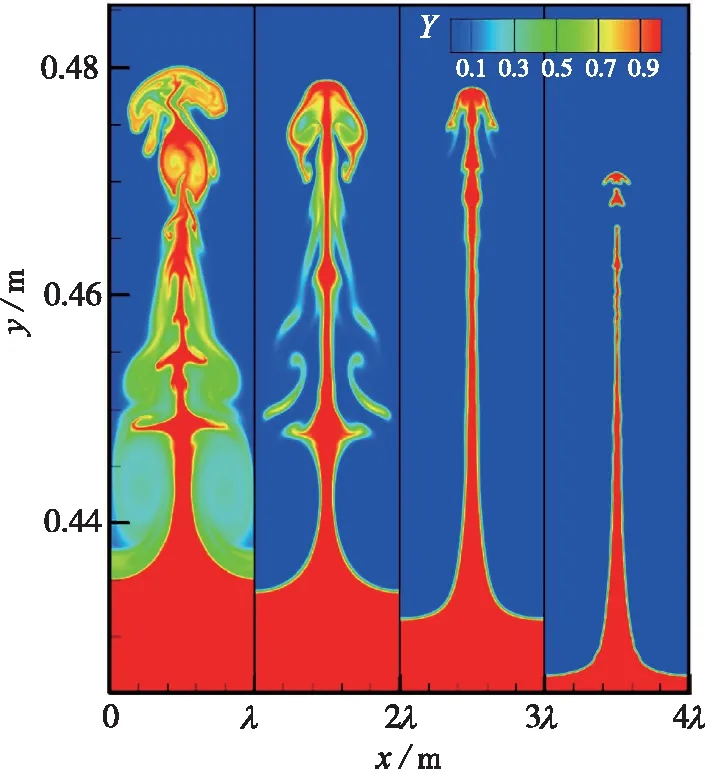
(c) t=0.8 ms图4 不同时刻不同化学反应活性的火焰界面形态Fig. 4 Patterns of flame interface with different chemical reactivities at different moments

在t=0.8 ms时， 由于反射激波和界面的相互作用， 加速了界面的失稳， 在化学反应冻结的条件下， 可以看到界面形态由A阶段中几何形状相对规则的“钉-帽-涡”结构发展成不规则的褶皱的界面结构， 在“钉”的两侧存在大量的涡结构， 这是由于反射激波掠过界面后， 界面上形成的斜压涡量进一步诱导界面失稳。当加入了化学反应(Ea=50.0RT0)后，长“钉”两侧涡结构内的反应物逐渐被消耗， 并且界面下方的“泡”结构也随着反应活性的增强向下发展， 当活性最强(Ea=30.0RT0)时， 界面呈现出沿流向的细长“钉”结构， 界面形态恢复沿中心轴线(x=λ/2)的对称性。

图5给出了3个典型时刻下， 介质不均匀性对火焰界面形态的影响， 该结果还和相同时刻下均匀介质中的火焰界面形态进行了比较。可以看到， 介质不均匀性对火焰界面形态的影响非常显著， 在入射激波作用后界面发展的初期(t=0.2 ms)， 不同于均匀流中典型RM不稳定初期所形成的“钉-帽-泡”结构， 在非均匀流的条件下，火焰界面形态呈现“钉-钉”结构， 混合区宽度增长速率明显大于均匀流中混合区宽度增长速率， 这是由于密度沿x方向分布的不均匀性导致激波的传播速度不同， 即激波在中心轴线上的流向传播速度明显大于在边界处的流向传播速度， 该速度差使得混合区沿流向产生拉伸。

图6进一步给出了界面附近的涡量幅值|ω|=|∂v/∂x-∂u/∂y|的分布， 可以看到在均匀流的条件下， 涡量主要分布在火焰界面附近， 而在非均匀流的条件下， 曲面激波在向上运动的过程中， 由于斜压效应导致整个波后流场存在复杂的涡量场，x=0～λ/2时界面上方的涡量方向为逆时针，x=λ/2～λ时界面上方的涡量方向为顺时针， 互为反向的旋涡同时诱导界面向上运动。到t=0.5 ms时(图5(b))， 两种条件下混合区宽度的差值进一步增大， 界面呈现出长“钉”的形态， 并且在“钉”的上端由于被两侧流场中涡的旋转所诱导开始出现失稳。当反射激波掠过火焰界面后(t=0.8 ms， 图5(c))， 可以看到非均匀流条件下， 界面呈现无规则的破碎形态， 表明火焰界面的失稳向着小尺度结构甚至是湍流混合方向发展。

(a) t=0.2 ms(b) t=0.5 ms(c) t=0.8 ms图5 不同时刻不同均匀性的火焰界面形态(每幅图中左图代表均匀流， 右图代表非均匀流)Fig. 5 Patterns of flame interface with different inhomogeneities at different moments(Left one denotes homogeneous flow, right one denotes inhomogeneous flow in each figure)

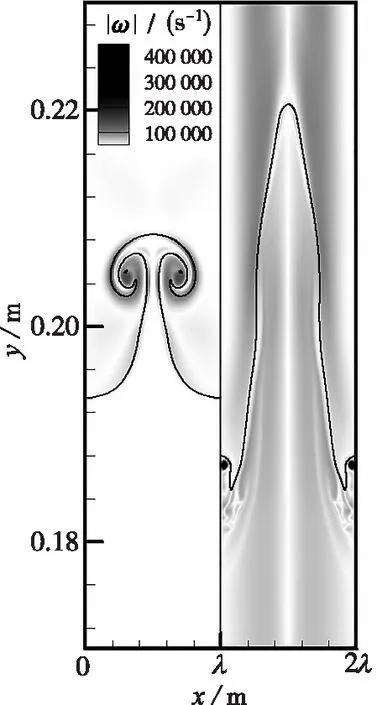
图6 t=0.2 ms时界面附近涡量分布对比(实线为反应物组分Y=0.5的等值线)Fig. 6 Vorticity magnitude among cases with different inhomogeneities at t=0.2 ms(the contour line is the reactant mass fraction of 0.5)

2.2 混合区宽度分析

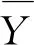
图7给出了不同反应活性条件下， 界面扰动增长的混合区宽度(WMZ)随时间的变化规律。可以看到， 所有条件下的界面， 在入射激波的作用下， 其混合区宽度都经历了一个初始增长的过程， 随着反射激波的再次作用(约0.6 ms时刻)， 界面混合区宽度在激波的压缩下有所减小， 之后又开始增长。在入射激波作用阶段(0～0.6 ms)， 初期不同活性条件下的混合区宽度增长是相似的， 随着时间的推移， 不同的化学反应活性的影响逐渐显现出来， 活性较强(Ea= 30.0RT0)的情况增长最快， 冻结流的情况增长最慢， 但均呈现线性增长的形式。当t=0.5 ms时， 可以看到Ea= 30.0RT0条件下的界面混合区宽度的增长曲线出现突然的下降， 这是由于较强的化学反应活性导致“钉”两侧涡结构内的反应物消耗殆尽， 从而使混合区宽度减小(见图4(b))。在反射激波作用阶段(0.65～0.85 ms)， 所有反应活性条件下的混合区宽度均呈现线性增长的趋势， 且增长速率高于入射激波作用阶段的增长速率。另一个明显的特征是： 反射激波作用阶段下混合区宽度的增长对初始反应活性依赖较弱， 这与界面上、 下两端的化学反应消耗的效应相互抵消有关， 由于上、 下两端的反应效应抵消， 因此混合区宽度的增长仅与流动特性相关。已有的研究表明[11,13-14]， 反射激波作用下的混合区界面宽度对初始条件的依赖较弱， 因此导致了本文混合区宽度增长的一致性。

图8显示了化学反应活性相同的条件下(Ea=38.2RT0)， 流场的均匀性对混合区宽度的影响。可以看出， 不均匀性对界面扰动的发展有很大的影响。在入射激波作用阶段， 不均匀介质下的混合区宽度增长很快，这是由于不均匀介质具有更大的涡量， 从而导致了更强的诱导速度(参见图5(b))；在反射激波作用阶段， 可以发现不同介质条件下的混合区宽度的增长速率也呈现出较为一致的趋势， 这也说明， 混合区上下界面处的化学反应消耗效应相互抵消， 因此界面发展仅与流动有关。

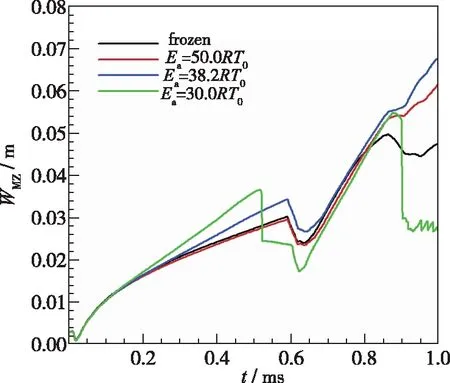
图7 不同化学反应活性下混合区宽度随时间的变化Fig. 7 Time histories of width of mixing zone with different chemical reactivities

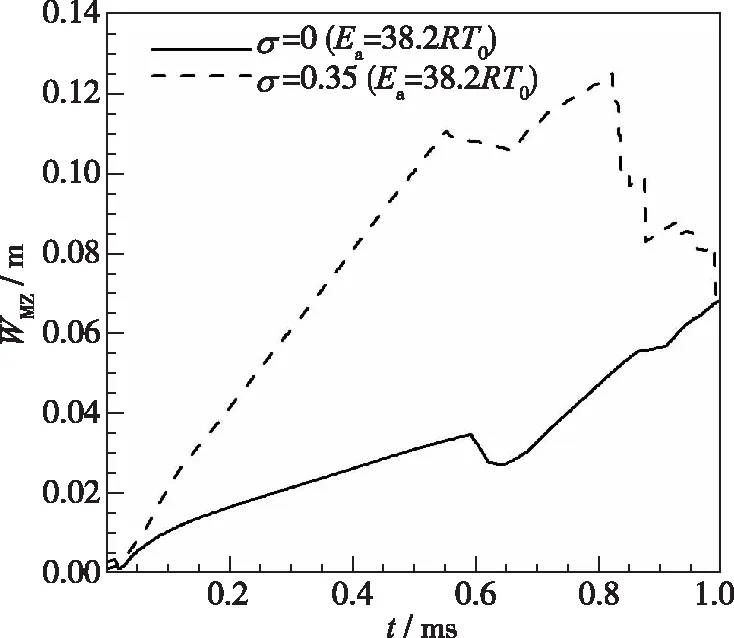
图8 不同均匀度下混合区宽度随时间的变化Fig. 8 Time histories of width of mixing zone with different inhomogeneities

2.3 时间尺度分析

以上分析表明， 在反应性RM不稳定发展过程中同时伴随着流动、 化学反应及其分子输运等过程， 这些过程会同时影响预混火焰界面的发展。为分析不同反应活性和介质均匀性条件下， 这些过程的影响规律， 本文还进一步从时间尺度的角度进行了分析。由于在激波与预混火焰相互作用的过程中， 界面扰动增长的大尺度流动主要由斜压效应形成的涡量所主导， 因此表征大尺度流动的特征时间可以表示为

τf=1/<Ω>

其中，<Ω>为混合区内涡量幅值的系综平均。另一方面， 表征化学反应的时间尺度可以表达为

τm=1/<χ>=1/<α|∇Y|2>

其中， <χ>为混合区标量耗散率的系综平均，α为扩散系数， ∇Y代表标量的浓度梯度。这样， 通过比较在反应性RM不稳定过程中3种时间尺度的变化规律， 可以进一步确定反应活性与介质不均匀性对混合特性的影响。对上述3种时间尺度， 其值越小， 代表的过程在RM不稳定发展过程中所起到的作用就越重要。

图9(a)～(c)分别给出了本文所有算例条件下， 上述3种时间尺度随时间的变化过程。根据图9(a)流动时间尺度的结果可以看出， 在入射激波和第一道反射激波分别与界面相互作用的两个阶段中， 均是化学反应活性最强时的流动时间尺度最大， 而非均匀条件下的流动时间尺度最小。这说明在激波和界面相互作用的过程中， 较强的化学反应可以弱化流动对界面扰动发展的影响， 而流场的非均匀性则可以强化流动对界面扰动发展的影响。

(a) Flow time scale

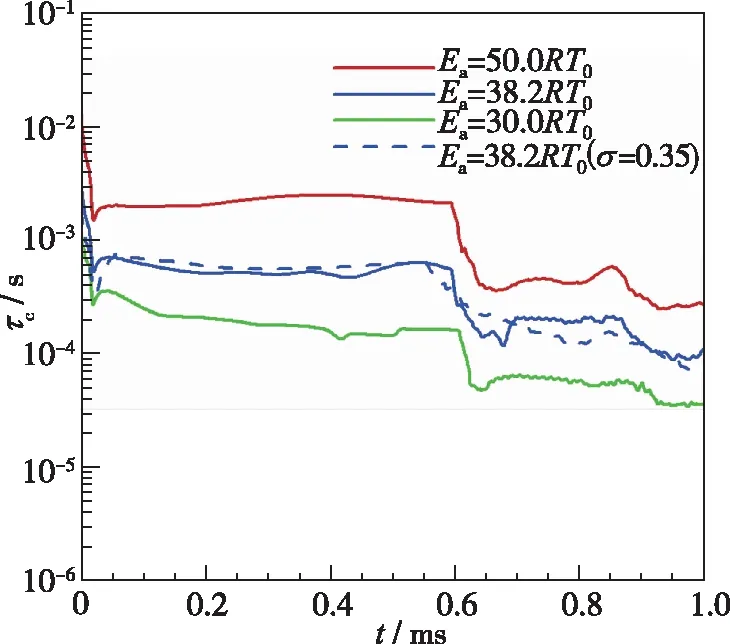
(b) Chemical reaction time scale

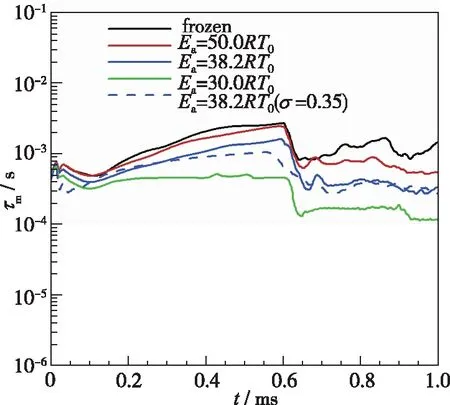
(c) Mixing time scale图9 RM不稳定发展过程中不同时间尺度的变化Fig. 9 Time histories of different time scales in RM instability development

此外， 由图9(b)中4种条件下反应流化学反应时间尺度的对比可以发现， 化学反应时间尺度随着活化能的增加而逐渐增大， 在相同活化能(Ea=38.2RT0)时， 均匀流(蓝实线)和非均匀流(蓝虚线)的化学反应时间尺度基本类似， 表明流场的不均匀性不会对化学反应产生本质上的影响。图9(c)中τm代表了分子输运引起的小尺度混合过程， 随着化学反应活性的增强，τm有所减小， 表明小尺度混合的效应有所增强， 同时也可以看出流场的非均匀性不会对小尺度混合产生明显影响。

综合图9(a)～(c)对比分析可知， 在本文所讨论的激波与火焰界面相互作用的两个阶段， 大尺度流动的时间尺度最小， 表明在本文的研究条件下， 大尺度流动对反应性RM不稳定的影响是最大的。

3 结论

本文采用带单步反应的高精度计算格式， 数值研究了入射激波及其反射激波与预混火焰界面相互作用的RM不稳定过程， 重点考察了介质的化学反应活性和不均匀性对界面扰动发展的影响， 得到的主要结论如下：

1)在均匀介质中， 正弦形预混火焰界面在平面入射激波作用后沿流向不断拉伸， 除了由于RM不稳定所贡献的混合区长度的增长外， 随着化学反应活性的增强， “钉-帽”结构向上发展， “泡”结构向下发展， 导致混合区增长速率随反应活性的增强而加快。在非均匀介质中， 平面火焰界面在曲面入射激波作用后同样沿流向不断拉伸， 但界面形态呈现双“钉”结构， 并且逐渐发展成不稳定的细长“钉”结构， 在第一次反射激波作用后火焰界面破碎并趋向于小尺度结构。

2)在入射激波与界面作用的阶段， 均匀流条件下的火焰界面混合区宽度呈线性增长趋势， 且化学反应活性越强， 混合区增长越快；流场的非均匀性会大幅度提高火焰界面混合区的增长速率。在反射激波与界面作用阶段， 混合区的增长速率对反应活性和均匀性依赖较弱。

3)化学反应会抑制大尺度流动， 并且化学反应活性越强， 抑制效果越明显， 而化学反应的增强对小尺度混合则是起到促进作用。非均匀性会强化流动， 但是对化学反应和小尺度混合几乎没有影响。总的来说， 大尺度流动对反应性RM不稳定的影响最大。

下一步工作展望： 介质的非均匀性强化了大尺度流动， 但不同的介质非均匀性对火焰界面演化的影响尚不明确， 因此下一步工作会针对不同非均匀介质中的反应性RM不稳定过程做进一步的研究。