基于弯曲激波特征线法的两级压缩内收缩流场设计与分析

汤祎麒， 施崇广， 郑晓刚， 朱呈祥， 尤延铖

(厦门大学航空航天学院， 福建厦门 361101)

引 言

21世纪以来， 高超声速飞行器逐渐成为全球航空航天工业的前沿阵地。作为核心结构的进气道， 在捕获足够多空气的同时要实现高效的压缩， 保证整个推进系统产生足够的推力来满足宽Mach数的工作范围。有研究表明， 对Ma=5～7的碳氢燃料飞行器， 每提高1%的进气道压缩效率， 就可以增加3%～5%的推进系统比冲[1]。20世纪40年代， 国内外研究者提出了高流量捕获、 低外部阻力、 宽Mach数工作范围的三维内收缩式进气道， 相比于传统的二元式[2]、 轴对称式[3]和侧压式进气道[4]， 压缩效率显著提高。这类进气道往往通过在基准流场上流线追踪得到设计型面， 基准流场直接决定了进气道的气动性能。1942年， Busemann[5]提出了一种锥形内收缩流场， 包含一簇等熵压缩波和一道末端锥形激波， 总压恢复较高。但过长壁面和完全内收缩的特性导致其无法在低Mach数下启动， Mölder等[6-8]遂采用截短的型面降低黏性损失， 并通过流线追踪提升起动特性。岳连捷等[9]利用NURBS样条曲线和ICFA(internal conical flow A)流场组合出总压恢复最大的基准流场。为提高流场出口均匀度， 郭军亮等[10]基于Busemann流场与ICFA流场组合设计了ICFC(internal conical flow C)和ICFD(internal conical flow D)流场。Matthews等[11]基于特征线法(method of characteristics， MOC)设计了等内收缩角、 等压力的轴对称基准流场。南向军等[12]结合特征线法反设计了壁面压力可控的基准流场， 对得到的进气道开展风洞试验[13-14]。朱伟等[15]基于此提出了壁面Mach数分布可控的基准流场设计方法。李永洲等[16]设计了一种中心体可控的双波入射内收缩基准流场。Malo-Molina等[17-19]采用能够在偏航和俯仰平面对气流双重压缩的三维无黏流场设计了一种新型的Jaws进气道。刘燚[20]和方兴军[21]设计了由出口Mach数或速度分布计算流场的特征线法， 韩伟强等[22]据此提出了由给定下游边界流场参数逆向求解基准流场的特征线法， 为基准流场的求解提供了新思路。卫锋等[23]发展了可实现消波的基准流场设计方法。美国Astrox公司的Kothari等[24]基于三维内收缩轴对称基准流场设计得到了Funnel型进气道。随着高超声速飞行器逐渐向一体化发展， 几何过渡变截面内收缩进气道逐渐兴起。Smart等[25-26]基于截短角度的倒置等熵喷管流场设计了矩形进口、 椭圆出口的内收缩进气道。谭慧俊等[27]发展了基于样条曲面的新型内通道设计方法， 不会对入射波依赖域内的型面产生影响。Gollan等[28]综合典型的设计方法设计了非常规进口、 椭圆出口的模块化进气道， 可用于锥形前体的一体化设计。上述方法只能达到几何上的变截面设计， 为实现设计状态的全流量捕获， 研究者逐渐把目光转向气动过渡， 为复杂乘波外形与内收缩进气道的一体化提供了可能。洛克西德·马丁公司设计的FALCON飞行器[29]采用了一种变截面的翼身融合进气道方案。尤延铖等[30]采用吻切轴对称理论基于非对称内收缩基准流场设计了变截面内乘波进气道， 可同时控制进、 出口截面形状。尤延铖等[31]还基于由部分Busemann流场和ICFA流场组成的基准流场提出了激波形状可以任意选取的变截面内乘波式进气道的设计方法。Xiao等[32]采用等收缩比的方法设计了一种新型变截面内乘波进气道， 通过较均匀的喉道截面压力分布实现了隔离段内的消波。

内收缩基准流场正朝着精细化设计的趋势发展， 但前文提到的基准流场及其设计方法仍存在一定缺陷： 一方面反设计用到的特征线法无法获得高阶的气动参数， 计算耗时较长， 不利于对流场的优化求解； 另一方面绝大部分流场是由一道入射激波和一道反射激波组成的双波结构， 激波压缩比例小， 且设计时需要给定壁面型线或沿程气动参数， 无法直接控制波系分布。Shi等[33]提出的弯曲激波特征线法(method of curved-shock characteristics， MOCC)能很好地解决前一个问题： 对于同样数量的网格节点， 相同精度下MOCC相比于MOC可以节省约90%的计算时间， 而优化问题往往需要求解上万个流场， 这时MOCC可以节省大约90%的计算资源。针对后一个问题， 在保持其他参数不变的情况下通过多级压缩可以在满足增压比和总压恢复的平衡下提高流场在高型面设计Mach数时的压缩效率。考虑到不同形状的激波曲线会对进气道的几何形状和气动性能以至发动机流量产生很大影响， 本文基于MOCC提出了一种激波型线和出口参数分布可控的两级压缩内收缩基准流场的反设计方法， 借助数值模拟验证了设计方法对任意弯曲波系结构的准确性。随后改变设计参数， 探索流场气动特征与性能参数的变化规律， 以及不同设计参数间的相互影响， 对涉及的关键问题进行研究。该方法的提出有望对后续任意三维激波的内乘波流场及进气道的设计与优化提供理论支撑。

1 基准流场设计方法

1.1 弯曲激波理论及弯曲激波特征线法

弯曲激波特征线法(MOCC)是基于弯曲激波理论建立的。该理论由Mölder提出， 1阶形式如下

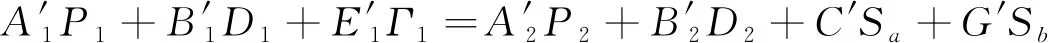
其中， 系数A，B，C，E，G是来流条件和激波角的表达式， 具体可参考文献[34]。下标1, 2分别代表波前和波后的流动条件,Sa和Sb分别为激波在流动面和流动垂直面的曲率, Shi等将方程两边对σ求导， 得到2阶弯曲激波方程， 方程及系数的推导详见文献[35]。

A″1P′1+B″1D′1+E″1Γ′1=
A″2P′2+B″2D′2+C″S′a+G″S′b+const″

A‴1P′1+B‴1D′1+E‴1Γ′1=
A‴2P′2+B‴2D′2+C‴S′a+G‴S′b+const‴

当来流条件已知， 通过弯曲激波理论可以求解弯曲激波波后气动参数及梯度， 但其作为高阶R-H理论仅适于激波附近区域。Shi等提出了MOCC来扩展其应用范围， MOCC采用流线-特征线坐标系， 方程(1)～(6)组成了此法的偏微分方程

压力梯度

P=(∂p/∂s)/(ρV2)

(1)

流线曲率

D=∂δ/∂s

(2)

沿流线的动量方程

(3)

沿流线的能量方程

(4)

沿特征线方向的动量方程

=ρV2(Pcosμ∓Dsinμ)

(5)

沿特征线方向的流量方程

(6)

由于气动参数沿流线/特征线偏微分等价于全微分， 故可将上述控制方程转换为全微分方程

(7)

对1阶常微分方程组(7)两边沿特征线或流线方向求导可得2阶常微分方程组。

利用MOCC， 弯曲激波理论可应用于弯曲激波波后全流场气动参数及导数的求解。不同于特征线法需要1条流线和2条特征线迭代求解相容方程， MOCC仅需要1条流线和1条特征线迭代求解控制方程， 消除了计算误差的累积。通过建立压力梯度、 流线曲率与气动参数的直接联系， 合理利用梯度信息等高阶变量， 不仅可以减少网格数量、 提高计算效率， 还可以用来研究相关物理现象， 具有高精度的优势。

1.2 两级压缩内收缩基准流场反设计

鉴于MOCC在求解平面和轴对称流场中的高精度， 可用于超声速流场的反设计。进气道设计分为两个部分： 1)确定无黏超声速流场； 2)采用流线追踪技术设计无黏进气道。第一步是设计的核心， 因为进气道性能与超声速流场直接相关， 而入射和反射波又直接决定了流场的性能。所以在已知激波或出口参数的情况下， 可在生成进气道之前算出无黏进气道的总压损失。考虑到实际应用价值， 超声速流场的反设计至关重要。由于激波与能量损失有着直接关系， 因此在理论设计中可以通过给定入射激波直接控制气动性能。内部流动时入射激波撞击壁面会发生激波反射， 为了控制总能量损失， 发展了已知入射和反射激波的反设计方法。本文的设计方法给定了两道入射激波的型线方程、 反射激波的激波角及其波后气流角分布。

基于MOCC的两级压缩内收缩流场反设计流场可分为“三波四区”， 如图1所示。流场主要包含3组激波压缩区(AO′B′,B′O′C和O′DE)和1组等熵压缩区(CO′D), 相比于李永洲等[16]的双弯曲入射波基准流场少了一个等熵压缩区， 所以流场长度进一步缩短， 压比也会显著提升。图1中红色实线分别代表2道入射激波(AO和B′O′)和1道反射激波(O′D), 绿色虚线代表各部分结尾特征线， 紫色实线分别代表压缩壁面和中心体型面， 黑色点划线为中心轴(与中心体型线之间的距离定义为中心体高度)。超声速流场的计算只是单元过程的不断重复， 反设计同样基于各单元过程， 下面对各区域的设计过程进行详细说明。

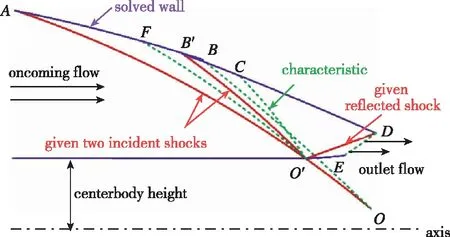
图1 基于MOCC的两级压缩流场反设计—(已知入射激波和反射激波)Fig. 1 Inverse design of two-stage compression flowfield based on MOCC(known incident and reflected shocks)

1.2.1 第1道入射激波波后依赖域ABO

内流中激波波后依赖域的求解主要涉及内点的单元过程， 如图2所示， 此时由1点发出的流线与由2点发出的逆右行特征线(C-)交于待求点3。其实内外流唯一的区别在于特征线的选取， 本文研究内收缩流场的设计， 故以内流为例， 2阶中心差分形式的常微分控制方程如下所示

(8)

其中， 上标“-”代表离散点气动参数的平均值。图2给出了MOCC平面和轴对称流场内点单元过程，红色、 紫色和绿色曲线分别代表入射波、 流线和特征线。给定来流条件和激波形状， 利用R-H关系式可以求解激波点1和2波后诸如压力和气流角等气动参数。基于求得的气动参数和激波曲率， 结合弯曲激波方程组， 可以获得点1和2波后气动参数的导数。当点1和2的物理特征确定之后， 待求点3的位置可根据如下几何方程求解

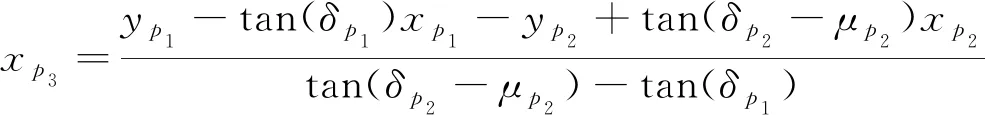
其中, 下标p1,p2,p3代表单元点1， 2和3。一旦单元点3的位置确定， 相关气动参数初值便可通过点1的Taylor展开求解

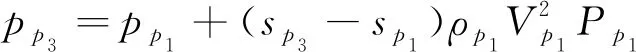
图2 内点单元过程Fig. 2 Interior unit process of MOCC

最后利用点1， 2， 3的气动参数求解方程组(8)， 更新点3的气动参数。如果点3的新旧气动参数差值大于设定残差， 就根据离散点之间的平均值迭代求解点3的位置及气动参数， 直到误差小于设定残差。经过几轮迭代， 点3的气动参数及其导数将逐渐收敛至真实值附近。

在给定来流参数和激波型线AO后， 通过斜激波关系式定义了一条非特征线的边值线AO。利用MOCC即可求出区域ABO的流场参数并得到壁面型线AB。 步进过程如图3所示： 已知激波点B1， …，Bn， 由B1和B2依照上述的单元过程确定A2， 重复上述过程可以依次确定A3， …，An。过Bn和An的流线即为产生给定激波的内收缩壁面。

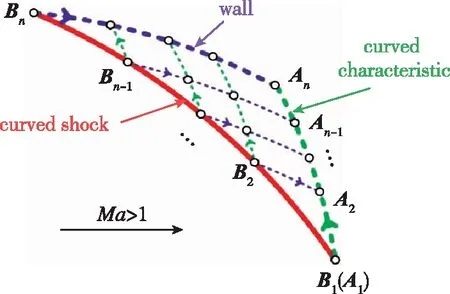
图3 MOCC步进过程Fig. 3 Step process of MOCC

1.2.2 次级激波压缩区域B′O′C

在求得第1道入射波的依赖域ABO后， 取过O′的水平线为中心体，O′即为两道入射波的共同反射点， 过O′做任意弯曲激波B′O′为第2道入射波。事实上， 即使第2道激波的型线为直线， 由于其波前气流的不均匀性， 其上各点的激波强度仍是不同的。选取时只需保证B′O′在ABO内部且满足激波角大于Mach角的要求， 由Mach角与激波角的关系可知， 第2道入射波必在Mach线O′F下游， 这可以为我们的选择提供一定程度的限制。注意无论是第1道入射波的端点O还是第2道入射波的端点O′， 在选择时都要考虑到高度(即到轴线的距离)的限制， 太低会导致激波强度过大， 产生Mach反射， 这是我们设计时不希望看到的。激波B′O′上的波前参数由插值求得， 显然其形状并不受O′O段的影响。通过斜激波关系式求出B′O′波后内点参数， 进而依照1.2.1节的方法求出激波B′O′的依赖域B′O′C及压缩型面B′C， 注意B′C与第1段壁面的B′B部分并不重合。

1.2.3 等熵压缩区域CO′D

同样利用MOCC可求得区域CO′D的流场参数及壁面CD。首先将离散网格点分为内点和反射激波点， 前者仍按照1.2.1节中内点过程进行求解， 激波点的求解则不相同， 相应的2阶中心差分格式微分控制方程如下所示

(9)

其中， 上标“-”表示离散点气动参数的平均值。

图4展示了MOCC激波点求解的单元过程。反射激波， 流线和特征线分别用红色、 紫色和绿色曲线表示。尽管单元点1和2的气动参数及其导数为已知边界条件， 激波点单元过程仍然需要一个额外的条件来完成求解。该条件需要与反射激波相关， 例如反射激波形状或者激波波后参数等。考虑到实际应用， 大部分超声速流场都要求出口气流水平。因此， 本节以反射激波出口气流水平作为额外边界条件介绍单元过程。需要注意的是， 其他与反射激波相关的边界条件也可以作为相应已知条件。单元过程的具体细节也会因为边界条件的不同有些许差异, 但整体流程是类似的。由于单元点1和2处的物理信息已知， 因此， 激波点单元过程首先需要确定单元点3的位置和曲率。通过弦截法可以获得单元点3的激波角， 进而利用如下所示的几何方程可以确定单元点3的位置

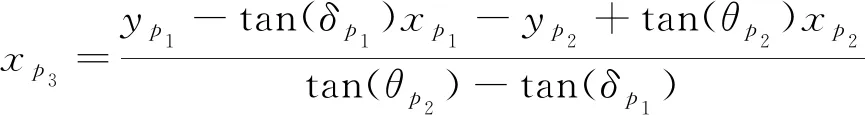
确定位置后， 利用R-H关系式结合激波已知的物理信息可以得到单元点3处的初始气动参数。下一步， 利用单元点1， 2， 3的气动参数求解2阶中心差分形式的控制方程组(9)， 更新单元点3处的气动参数。单元点3的气动参数将会不断迭代更新直到残差小于设定值。几轮迭代之后， 相应的气动参数及其导数将逐渐收敛至真实值附近。

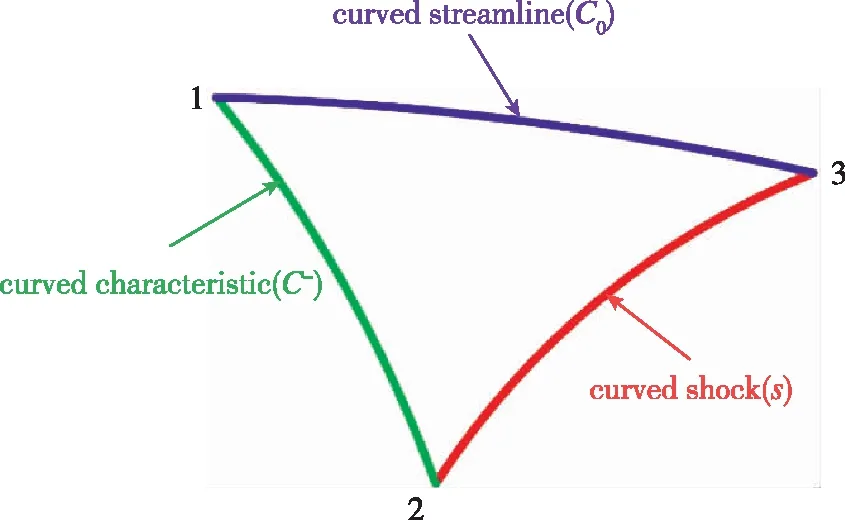
图4 激波点单元过程Fig. 4 Shock unit process of MOCC

1.2.4 反射激波波后依赖域O′DE

确定反射激波O′D后， 利用斜激波关系式求出波后流场参数， 区域O′DE以及中心体型线O′E同样只需采用类似于1.2.1节中的MOCC内点单元过程进行求解， 只不过此时选取的是逆左行特征线(C+)， 待求点3由点1发出的流线与点2发出的逆左行特征线相交， 如图5所示。

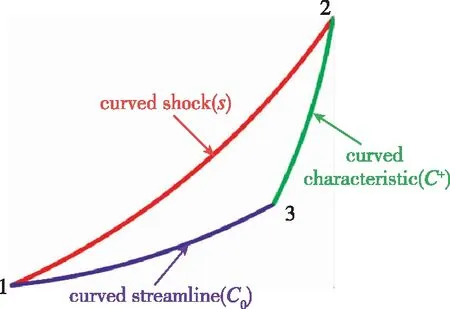
图5 内点求解单元过程(外流)Fig. 5 Interior unit process of MOCC(outflow)

MOCC通过构建高阶控制方程， 搭配弯曲激波方程组， 可用于高精度求解平面和轴对称超声速流场。同时， 本文的两级压缩设计使得在第2道激波和反射激波前的来流都是非均匀的， 这也证明了MOCC的普适性。注意到基于MOCC得到的两级压缩内收缩流场与最左侧来流的均匀性无关， 但设计流场求解时有可能出现网格线相交， 也即同簇特征线相交的情况， 这说明给定的激波和流场参数分布不存在对应的物理解， 需要调整输入重新设计。

综上所述， 本文基于MOCC的两级压缩内收缩流场设计方法不仅能够确保两道激波符合给定型线方程， 实现流场波系结构的主动控制； 还能保证反射激波波后流向角的水平分布， 便于参数均匀的反设计； 与通过给定壁面沿程参数分布或直接给定等熵压缩段壁面型线来求解流场的方法存在很大不同。由于进气道的流量特性取决于入射激波的形状和位置， 因此只要基准流场的入射激波完全将进口封闭， 就可以实现全流量捕获。反射激波的强度和位置仅影响下游的气动特征， 并不会改变流场的内乘波特性。

2 设计方法数值校验暨超声速流场反设计

随着高超声速飞行器的工作范围不断扩大， 为了兼顾宽来流Mach数下的总体性能(尤其是巡航点)， 其型面设计Mach数将不断增加[16]。对于内收缩进气道， 此时气流仅通过两道波主压缩(等熵压缩区域的压缩能力并不强)， 造成的激波损失将显著增大。而且其出口压比受进气道长度的限制并不会很高。在二维和轴对称进气道设计中， 两级压缩内收缩流场便能较好地解决上述问题。

2.1 超声速流场反设计

基于弯曲激波理论的MOCC可用于高精度求解平面和轴对称超声速流场， 来流经过壁面偏转时会在前缘产生入射激波， 随后入射波撞击中心体产生反射激波， 反设计分为入射波和反射波两部分。首先给定两道入射波的激波型线方程， 利用R-H方程和弯曲激波方程根据来流条件可以求解波后气动参数及梯度， 本文中来流条件均设置为 26 km 海拔理想大气， Mach数6。对于每段离散激波， 通过内点过程不断迭代获得收敛的气动参数及梯度， 然后沿流向推进对第1道入射波部分进行求解， 被第2道入射波截取后的流场特征如图6上半部分所示。在得到第2道入射波部分后， 结尾特征线的参数将作为求解反射激波部分的边界条件。由于中心体高度不同， 反射波几何方程也不相同， 这里通过给定反射激波角变化来定义反射波的形状， 而反射波后的流动方向保持水平。使用激波过程可求解反射波附近的气动参数， 进而利用内点过程计算壁面、 反射波和特征线包围的区域， 计算过程终止于壁面和反射波的交点处。由于入射波的不确定性， 壁面长度无法在求解之前限定而只能在求解结束后获得。Mach杆后的亚声速区域会降低流场的气动性能， 所以内收缩流动中通常设计中心体来避免Mach反射， 中心体高度的不同也会导致求解域范围产生差异。最后借助反射波附近参数通过内点过程求解反射波波后流场， 图6下半部分展示了完整的内收缩流场流动特征。

由于流动形式的不同， 即使在相同的入射波下平面和轴对称反设计流场也具有不同的流动特征。梯度是造成这种现象的主要原因， 相关分析见文献[33]， 这里不再赘述。

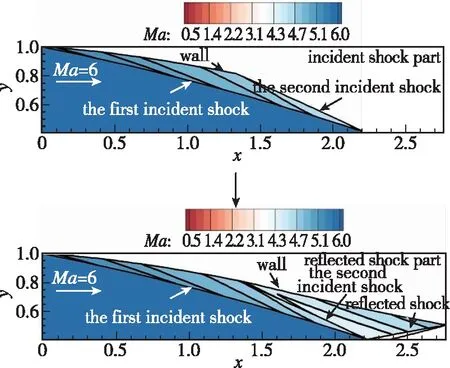
(a) Planar internal flowfields

(b) Axially symmetric internal flowfields图6 均匀来流已知入射和反射激波超声速流场反设计Fig. 6 Inverse design of planar and axially symmetric internal flowfields with shocks in uniform flows

本节将分别针对第1道入射波弯曲、 第2道入射波平直和双弯曲入射激波的情况， 以均匀来流已知激波分布的平面和轴对称内收缩流动为例， 根据1.2 节的设计方法， 将MOCC求解的流场与CFD结果进行比较。进行数值验证的同时完成超声速流场的反设计。

CFD在正设计中具有广泛应用， 已被证实是一种精确的方法， 本文利用CFD模拟了给定激波分布的内收缩流动， 以验证设计方法的精度。由于基本流场的求解中忽略了黏性， 因此CFD计算中选择无黏模型， 无黏通量利用Roe-FDS算法计算， 控制方程采用完全隐式格式的2阶迎风离散法求解。结构化网格及边界条件如图7所示， 为了清晰起见， 实际网格密度已降低。对近壁面网格采用局部加密， 并在出口水平延伸一段距离用来观察结尾的反射激波串。经过网格无关性验证后， 全计算域实际网格数量由各自的尺寸决定， 分辨率足以获得收敛结果。入口和出口分别设置为压力远场和压力出口边界条件， 来流设置为理想气体， 壁面采用滑移边界条件。收敛标准是监控变量残差下降3个量级且进出口流量守恒。

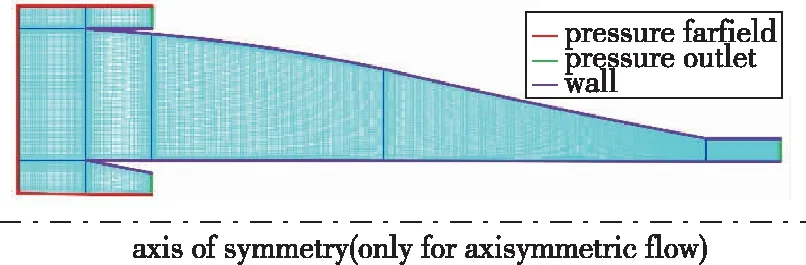
图7 结构网格和边界条件Fig. 7 Grid structure and boundary conditions

2.2 弯直入射两级压缩基准流场

2.2.1 平面流动

本算例中第1道入射波的型线方程为y=-0.1x2-0.2x+1， 第2道入射激波的型线方程为y=-0.892 1x+1.865 3， 反射激波角的变化率为dθre/dx=-0.2， 中心体高度为0.404 1， 质量平均的出口压比和总压恢复系数分别为 128.48 和 0.350 7。

图8显示了由激波分布计算得到的平面内收缩流场流动特性， 黑色实线代表CFD结果的等参数线和激波， MOCC的等参数线和激波则分别用红色虚线和白色虚线表示。使用MOCC获得的平面流场与CFD结果具有十分相似的流动特征， 两道入射激波按照预设汇聚于(1.638， 0.404)， 证明MOCC具有足够高的精度求解已知参数分布边界的平面超声速流场。

图8 弯直入射波平面内收缩流场Fig. 8 Planar internal flowfield with one direct incident shock and one curved shock

分别提取壁面和中心体处的压比参数进行对比， 如图9(a)所示， 其中散点和线条分别代表CFD和MOCC的结果， 壁面和中心体处压力分布则用黑色和红色进行区分。可以发现无论是数值还是压升规律， 无论是壁面还是中心体， MOCC的结果均和CFD吻合得很好。此外， 如图9(b)所示， 分别提取了CFD结果流场在反射波后和喉道处的流向角分布， 红色实线代表喉道处的流向角分布， 反射波后的流向角分布则用黑色虚线表示。可以发现反射波后的流向角与水平偏差不超过0.015， 即使继续延伸至喉道， 这个差值也不超过 0.04， 很好地保持了给定的流向角分布规律。

2.2.2 轴对称流动

本算例中第1道入射波的型线方程为y=-0.03x2-0.2x+1， 第2道入射激波的型线方程为y=-0.510 0x+1.427 2， 反射激波角的变化率为dθre/dx=0.2， 中心体高度为0.591 9， 质量平均的出口压比和总压恢复系数分别为 50.36 和 0.628 7。

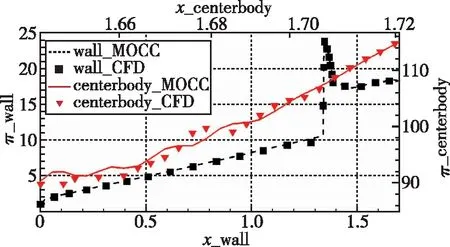
(a) Pressure distribution along the wall and centerbody

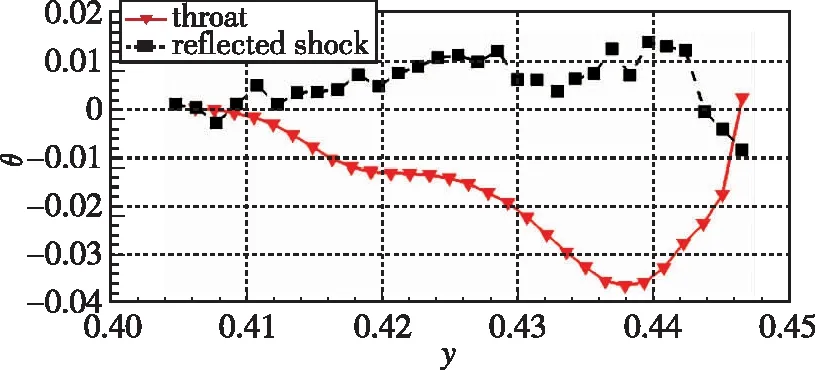
(b) Deflection angle distribution along the throat and just behind the reflected shock图9 平面内收缩流场设计参数对比Fig. 9 Comparison of design parameters of planar internal flowfield

图10显示了由激波分布计算得到的轴对称内收缩流场流动特性， 相关线条定义与平面情况一致。使用MOCC获得的轴对称流场与CFD结果具有十分相似的流动特征， 两道入射激波按照预设汇聚于(1.638， 0.592)， 证明MOCC具有足够高的精度求解已知参数分布边界的轴对称超声速流场。

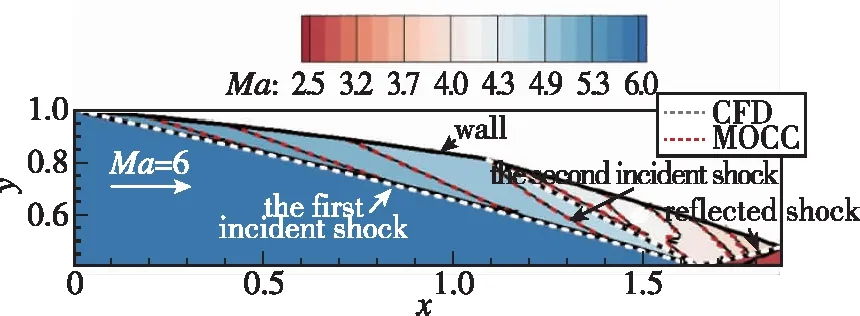
图10 弯直入射波轴对称内收缩流场Fig. 10 Axisymmetric internal flowfield with one direct incident shock and one curved shock

分别提取壁面和中心体处的压比参数进行对比， 如图11(a)所示， 相关线条定义与平面情况一致。MOCC的数值和压升规律结果在壁面和中心体上的分布均与CFD一致。分别提取了CFD结果流场在反射波后和喉道处的流向角分布情况， 如图11(b)， 发现反射波后的流向角与水平偏差不超过0.006， 即使继续延伸至喉道， 这个差值也不超过 0.035， 流向角保持设计的水平分布。

(a) Pressure distribution along the wall and centerbody

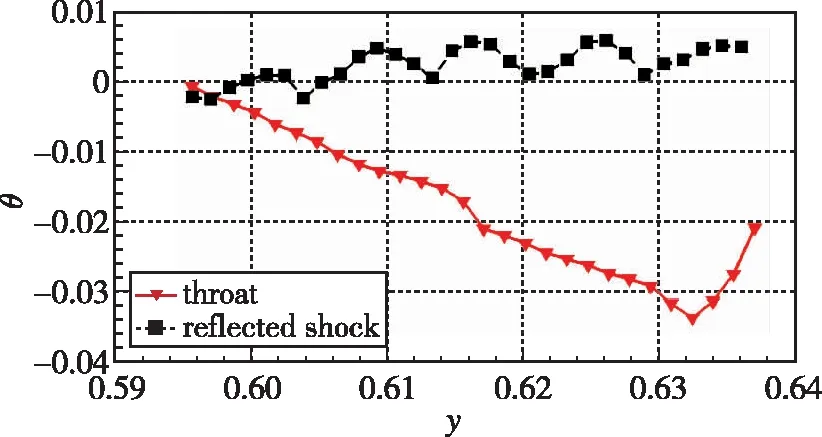
(b) Deflection angle distribution along the throat and just behind the reflected shock图11 轴对称内收缩流场设计参数对比Fig. 11 Comparison of design parameters of axisymmetric internal flowfield

此外， 观察CFD结果中延伸段内的流场， 如图12所示， 可以发现反射激波准确打在肩点(1.862， 0.642)处， 同时水平段内存在不断反射的激波串， 但由于激波强度较弱， 所以暂未做消波处理。

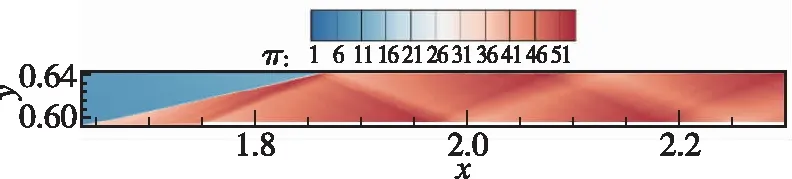
图12 水平延伸段反射激波串Fig. 12 Reflected shock train in the horizontal extension

2.3 双弯曲入射两级压缩基准流场

双弯曲入射两级压缩基准流场是最普适的情况， 本文提出的设计方法可以用于对任意波系结构的两级压缩流场的反设计。本节对理论求解的双弯曲入射激波流场进行数值验证， 分别以平面和轴对称流动为例。平面算例中第1道入射波的型线方程为y=-0.03x2-0.2x+1， 第2道入射激波的型线方程为y=-0.023 1x2-0.376 3x+1.358 1， 反射激波角的变化率为dθre/dx=-0.15， 中心体高度为 0.406 3， 质量平均的出口压比和总压恢复系数分别为13.37和0.747 2。轴对称算例中第1道入射波的型线方程为y=-0.03x2-0.2x+1， 第2道入射激波的型线方程为y=-0.060 1x2-0.225 1x+1.204 9， 反射激波角的变化率为 dθre/dx=0.2， 中心体高度为0.406 3， 质量平均的出口压比和总压恢复系数分别为53.10和0.695 8。

由图13可以看出， 此时两道入射激波都是曲线， 尽管第2道激波的弯曲程度并不明显， 这是因为要满足激波角大于Mach角的要求， 因此若激波弯曲程度过大， 会导致在靠近壁面处激波角过小。Mach数云图和等值线吻合良好， CFD结果的3道激波及反射点、 喉道点、 壁面转折点等对应特征点均与理论值十分接近。以反射点为例， 由于本算例中平面和轴对称流场的两道入射激波在设计时具有相同的交点， 故图13(a)中平面流场和图13(b)中轴对称流场的反射点均为(2.226， 0.406)， 与设计一致。综合上述数值验证的结果， 可以证明本文的反设计方法对任意满足物理解的激波型线组合都是适用的。

(a) Planar

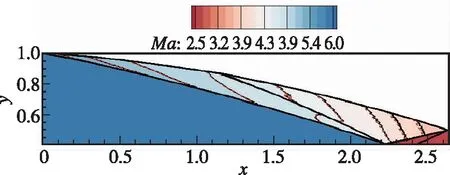
(b) Axisymmetric图13 双弯曲入射波内收缩流场Fig. 13 Internal flowfield with double curved incident shocks

3 两级压缩基准流场性能研究

本章利用上述程序设计了一系列轴对称两级压缩基准流场， 并研究了第2道入射激波激波角分布(以弯曲系数为代表)和反射激波激波角分布(以激波角沿流向变化规律为代表)对基准流场的气动和几何性能的影响。在对比基准流场的性能时， 以总收缩比、 内收缩比、 质量平均的喉道总压恢复系数和出口压比为主要标准。

3.1 第2道入射激波激波角分布的影响

本节根据先前研究结果选取第1道弯曲激波型线方程为y=-0.03x2-0.2x+1， 反射激波激波角系数取为 dθre/dx=-0.379， 随后分别设计了一系列不同第2道激波激波角分布的基准流场用来做对比试验。在选择算例时为控制变量唯一， 本节固定第2道入射波的起始点(图1中B′)和反射点(图1中O′)位置， 这里选取B′位置为(1.081 9， 0.875 5)，O′位置为(1.637 9， 0.591 9)。通过改变第2道入射波弯曲程度来探究激波角分布对流场气动性能的影响， 这里弯曲程度用系数coc(coefficient of curve)表示， 定义如下

其中，xmid为弯曲激波B′O′中点的横坐标， 由定义可以看出， 随着弯曲程度的增加， 激波角在靠近中心体的部分增加得更快， 而在靠近壁面附近则变化平缓。由于受到Mach角的限制， 显然coc的选取不是任意的， 对于给定的来流，coc存在对应的上下限。针对本组算例，coc的取值范围为0～0.038。如图14(a)所示， 黑色虚线和红色实线分别代表流场增压比和总压恢复系数随coc的变化规律。流场几何参数随coc的变化规律见图14(b)， 流场总收缩比和内收缩比分别用黑色虚线和红色实线表示。

由图14(a)可以看出， 随着第2道入射波弯曲程度的增大， 增压比呈现单调上升趋势， 而总压恢复系数则随之下降， 且两者随coc的变化接近线性。这是由于随第2道入射波愈发弯曲， 激波强度随之增大， 对气流的压缩增强， 压比增加； 与此同时激波压缩区占比增加， 流场的总压损失增大， 总压恢复系数减小。另一方面， 如图14(b)所示， 随着coc的增加， 无论是总收缩比还是内收缩比都显著增加， 这是因为随着第2道入射波在靠近中心体处的强度增加， 气流在经过第2道入射波时的偏转角随之增大， 第2段壁面转折增加， 导致等熵压缩区减小， 反射激波所打肩点随之降低， 所以尽管入口型面保持不变， 总收缩比和内收缩比依然不断升高。需要注意的是， 总收缩比随coc增加得越来越快， 而内收缩比则越来越慢。

(a) Boost ratio and total pressure recovery coefficient

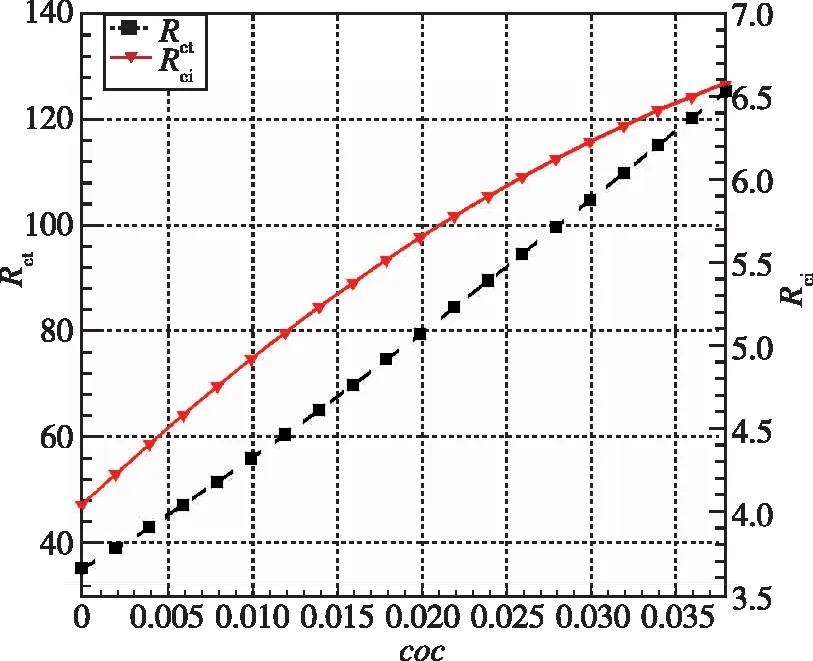
(b) Total shrinkage ratio and internal shrinkage ratio图14 流场性能随第2道入射激波激波角分布的变化趋势Fig. 14 Trend of flowfield performance with the shock angle distribution of the second incident shock

3.2 反射激波激波角分布

本节根据先前研究结果选取第1道弯曲激波型线方程为y=-0.03x2-0.2x+1， 第2道弯曲激波型线方程为y=-0.060 1x2-0.225 1x+1.204 9(相应的coc为0.04)， 随后分别设计了一系列不同反射激波激波角分布的基准流场用来做对比试验。反射激波激波角分布用系数cor(coefficient of reflect)表示， 定义如下

其中，θre为反射激波O′D的激波角， 由定义可以看出， 随着cor的增加， 激波角沿x方向增加得更快。同样地， 由于受到物理解的限制，cor的选取不是任意的， 对于给定的来流条件，cor存在对应的上下限。针对本组算例，cor的取值范围为 -0.165～3.82， 相应结果见图15， 相关线条定义与图14一致。

(a) Boost ratio and total pressure recovery coefficient

(b) Total shrinkage ratio and internal shrinkage ratio图15 流场性能随反射激波激波角分布的变化趋势Fig. 15 Trend of flowfield performance with the shock angle distribution of the reflected shock

由图15(a)可以看出， 随着反射激波的增强， 增压比随之增加， 总压恢复系数随之减小且变化速度有所下降， 基准流场压缩效率略微降低。这是由于两道入射波保持不变， 因此前两组激波压缩区保持不变， 随着反射激波激波角分布系数的增加， 反射激波在靠近肩点时的激波强度大幅增加。肩点位置随之前移， 使得等熵压缩区略微减小， 因此总压比和总压恢复系数的变化越来越慢。另一方面， 如图15(b)所示， 随着cor的增加， 总收缩比随之增加， 但到极限值时基本不变， 而内收缩比则先增加后减小， 这也是由于反射激波激波角分布的变化影响了等熵压缩区和反射激波波后依赖域的分配比例， 从而导致肩点位置和喉道高度的变化。

3.3 不同设计参数对彼此取值范围的影响

通过上述研究也可以看出， 在给定的设计参数下， 无论是coc还是cor都存在各自的取值范围， 超出这个范围则不存在对应的物理解。显然设计参数A的变化对设计参数B的取值范围是会有影响的， 进而会影响到流场的气动和几何性能， 这显然是流场优化设计需要考虑的， 本节就以coc和cor的变化及其对彼此取值范围的影响进行分析讨论。

首先保证3.1节中的其余设计参数不变， 分别取不同的cor， 如表1所示， 其中case 5即为3.1节中的算例。注意到在cor>-0.379时，coc的取值可以为负， 也即在凹向来流的第1道激波后， 第2道激波凸向来流。这虽然和平时的印象相悖， 但要注意到此时第2道激波波前来流非均匀， 因此不能仅根据第2道激波几何形状的凹凸来判断激波的强度变化， 而要结合激波角的变化。观察到随着cor的减小，coc的取值下限不断增加， 而上限则不变。我们知道激波角应大于波前Mach数对应的Mach角， 而若coc较大则会使得在靠近压缩面处第2道激波的激波角过小。因而在确定的第1道激波后条件下， 第2道激波coc的上限不变， 也即coc的上限主要受制于来流条件。但coc的下限则并不仅仅依赖于来流条件， 由于等熵区CO′D的存在而同时受到反射激波角分布的影响。随着反射激波沿流向强度递减速度逐渐提升， 靠近压缩面处的反射激波强度逐渐减弱， 顺流管向前追踪至第2道激波， 第2道激波靠近壁面处强度必须随之减小， 因而要求第2道激波的弯曲程度增加， 即coc的下限提升。

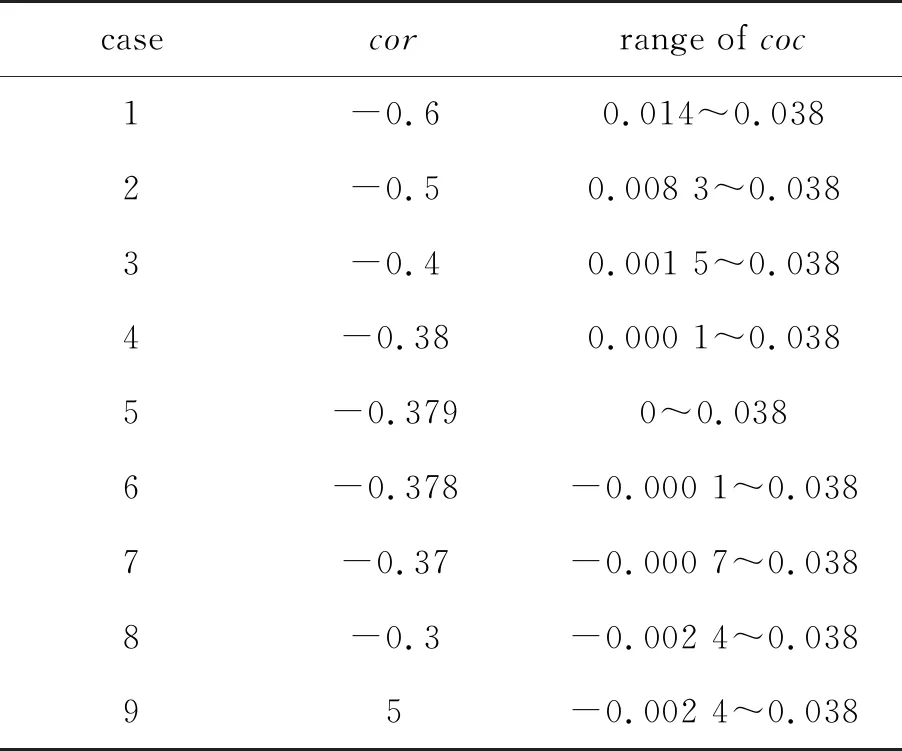
表1 不同cor下coc的取值范围

保证3.2节中的其余设计参数不变， 分别取不同的coc， 如表2所示， 其中工况2即为3.2中算例。受制于来流条件和出口不能跨声速的要求，coc的取值仅限于0.039～0.043， 观察到随着coc的减小，cor的取值上下限均有略微增加。与上述原因一致， 随着第2道激波弯曲程度的增加， 反射激波沿流向强度递减速度逐渐提升， 即cor上下限随之递减。

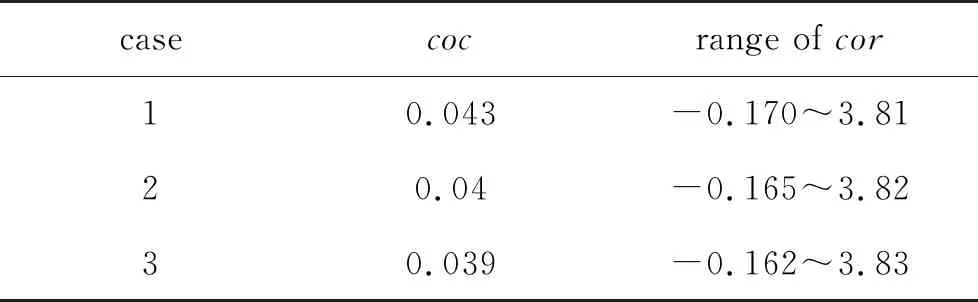
表2 不同coc下cor的取值范围

由本节的研究可以看出， 流场的气动参数随设计参数的改变而变化， 不同设计参数的取值范围也会受到彼此的影响， 进而影响流场性能。在无法直接由设计要求构造流场时， 基于MOCC给定激波的反设计在不需要进行复杂而耗时的CFD验证前就可以得到流场性能的预先估计， 从而在选择设计参数时不再盲目， 而是有的放矢。在给定进气道基准流场的气动和几何参数的需求后， 可以改变设计参数进行一系列的流场设计， 得到参数的变化规律， 在结果区间快速选取设计参数， 完成流场的优化设计。

4 结论

本文基于MOCC提出了一种两级压缩内收缩基准流场的结构与设计方法， 并通过数值模拟检验了设计方法对于任意弯曲激波波系结构的平面和轴对称流场的准确性， 主要得出以下结论：

1)基于MOCC的设计方法灵活且高效， 在具有高精度的同时可节省计算资源， 适用于任何波系组成的平面和轴对称流场设计。

2)给定入反射激波参数和出口流向角分布反设计流场压缩型面可以控制基准流场的波系结构和压缩效率， 保证双弯曲入射激波封口且出口气流均匀。

3)分别改变第2道入射激波和反射激波的激波角分布， 求解了一系列具有中心体的轴对称流场， 对比发现设计参数改变对流场气动和几何性能的影响规律， 以及不同设计参数的变化对彼此取值范围的影响规律， 便于设计前对流场参数的选取。

4)高求解精度和快设计速度使得MOCC成为超声速流场分析和反设计领域的良好候选者； 多波入射的结构使得流场长度缩短、 压缩效率提升， 对于拓宽基准流场的设计思路具有重要意义。未来将进一步开展流场设计的优化选取和基于此的内乘波进气道的相关研究。

致谢感谢国家自然科学基金(U20A3069, U21B6003)的资助, 也感谢1912项目组对本文工作的支持。