基于模拟退火遗传算法的并网微电网优化调度研究

冯悦雯，胡东阳

（国网湖北省电力有限公司神农架供电公司，湖北神农架 442400）

引言

近年来，在“碳达峰，碳中和”的战略引导下，清洁能源发电的发展又上了一个新台阶。我国相继构建了大规模的光伏电站、风力发电场等[1-5]。在“双碳”战略不断推进下，一些问题逐渐显露出来，如以光伏、风力发电为代表的分布式发电源，由于自然环境能源获取的不确定性，导致发电出力也存在着不确定性。在电网中注入高比例风光发电源后，会对电力系统电能质量的管控、继电保护，尤其是电网的稳定性等产生影响，在不良运行情况下甚至电网供电难以保证其可靠性[6-9]，从而影响用户的生产生活。因此，为了电网和各分布式电源可以更好地融合，微电网的分布式电源组织架构和与电网交互方式由此诞生。微电网是一个可与外部电网连接也可脱离电网的微型系统，其包含着基本的源、荷单元。其分布式电源主要包含风力发电机、光伏单元以及燃气轮机等。由上述单元构成的微电网在经济性、环境友好性上较传统能源系统有较大提升。同时，微电网可提高电力网络的灵活调度性。

对于微电网来说，多目标优化调度问题是其核心问题之一。为有目的性地进行电源的优化调度，国内外学者深入探究并得到不俗成果。文献[10]通过结合模拟退火方法和粒子群方法求解优化调度模型，增强了算法的收敛速度和全局搜索性能。文献[11]通过使用遗传算法对模型进行求解，该方法可以得到最优解但容易陷入局部最优解。文献[12]将Metropolis准则引入蜂群算法，建立求解微电网调度模型，但该模型只考虑了经济因素，并未综合考虑模型的环境保护的目标。

因此，建立微电网模型，并综合考虑微电网建设运行的经济性和环保性，以微电网建设运行成本和环境影响为目标函数，使用模拟退火遗传算法对模型进行求解。该方法能够对微电网各目标依据条件进行有效调度，具备快速求解调度问题的能力，同时避免了陷入局部最优解的困境，能够适配并解决在微电网场景下的调度问题。

1 退火遗传算法

模拟退火算法来源于固体退火原理，随着高温物体冷却，内部粒子由无序态走向有序，最后在冷却时达到稳定的基态。其核心思想是通过模拟高温物体退火过程找到组合优化问题近似全局最优解，跳出局部最优解后继续搜索直到得到全局最优解。遗传算法是一种经典的元启发式算法，也是一种基于自然选择和群体遗传机理的搜索算法。遗传算法在解决复杂组合优化问题有较好的表现，但算法容易陷入局部最优的结果。

模拟退火遗传算法(SA&GA)揉合了模拟退火算法和遗传算法，进一步提高了算法的性能。该算法能避免传统算法陷入局部最优解，是因其兼顾了模拟退火的全局搜索能力和遗传算法的局部搜索能力。为实现模拟退火遗传算法，首先通过遗传算法对种群进行编码，种群信息经过适应性函数评价后，得到经过选择、交叉和变异操作的新种群；接着将新种群用Metropolis准则确定种群状态，直至稳定。

总结得到模拟退火遗传算法的基本流程如下：

（1）参数确定：确定种群变异概率Pm、种群交叉概率Pc、降温迭代次数、最大迭代次数N以及初始温度T0、冷却温度Tf。

（2）最优个体选择：种群初始化并筛选出最优适应值F=fmin及所对应的最优个体。

（3）判断算法的收敛性：若算法收敛最优值和最优个体满足条件，则结束。反之继续进行操作，直至收敛。

（4）等温：每个个体会经历模拟退火中的等温操作，目的是为了得到新种群中的最小适应值f'min和最优个体；若f'min＜fmin，那么f'min会更新适应值F。

（5）当k＜N时，进行降温操作，步骤将回到3；否则结束计算，得到最优值。

2 微电网模型

微网模型主要包含可控制的燃气轮机出力、不可控的风光出力以及由蓄电池构成的储能单元[13-15]。

2.1 目标函数

2.1.1 运维成本目标函数

（1）微电网系统的燃料成本

燃料成本产生在燃料发电源的消耗原料上，下式为微电网中所有能源单元燃料的总费用。

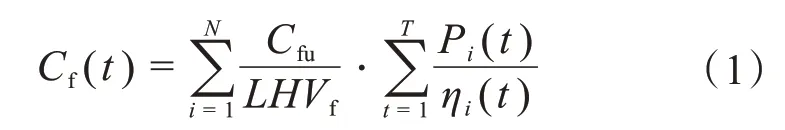
其中，Cfu为消耗燃料的市场价格；LHV为所需燃料低位热值；Pi(t)为系统第i个发电源在t时产出的有功功率；ηi(t)为系统第i个发电源在t时的燃料利用率。

（2）微电网系统的维护成本

微电网在运行工作时，对系统的检修维护是保证系统正常运行的必要手段。维护成本主要包含系统中的电源设备出现故障、维修人员费用等。

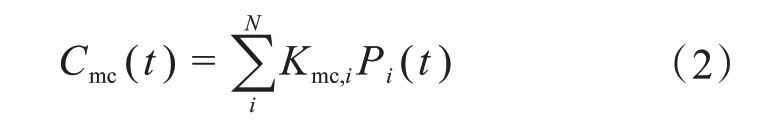
其中，Kmc,i为系统在i电压等级下的维修系数。

（3）投资成本

安置微电网系统中所需电源单元的必要投资成本称为总投资成本，其计算式如下。

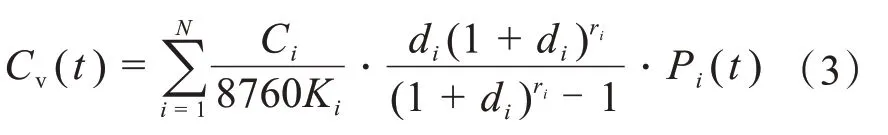
其中，N为系统电源的类型；Ci为安装发电源的安装成本；Ki为系统中第i个发电源的容量，8760Ki则为第i个发电源年产电量；di为系统中发电源计划折旧；ri为计划折旧年限。

（4）电能交换成本

电能交换成本主要是微电网连接电网并产生能量交流时，基于电价的电能交换成本：

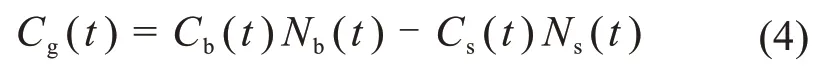
其中，Cb(t)为系统向电网购电价格；Cs(t)为系统向电网买电价格；Nb(t)、Ns(t)分别为购电量和买电量。

故得到系统运维总成本

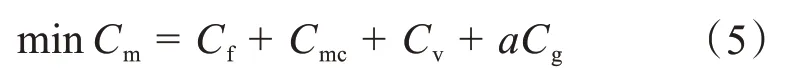
式中，a表示微电网与电网间的交互状态。当其取值为0时代表微电网系统不产生电网间能量交互，即表示离网或无功率交流；当a为-1时，表示微网向电网输送电能并基于电价获得售电获利；当a为1时，微网会向电网获取电能并基于电价产生一定成本。

2.1.2 环境成本目标函数

所涉及的环境成本的主要来源为微电网各设备在工作过程中产生对环境造成伤害的主要污染物，如CO、CO2、SO2、NOx等的处理成本。

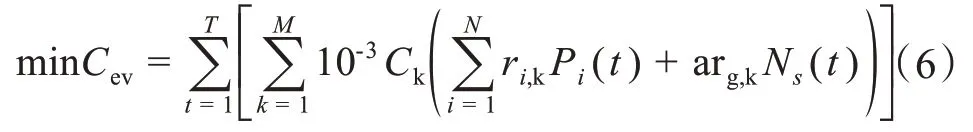
其中，Cev为总环境成本；Ck为处理k类污染物的单位成本；M为设备工作时产生污染物的类型；T为系统调度时段，最小单位为1 h；ri,k为系统第i个发电源单位有功产生的某污染物质量；rg,k为单位电能交换时产生的某污染物质量。

2.1.3 综合效益的目标函数

综合效益是将影响微电网建设因素周全考虑的必要途径。微电网短周期获益能力一般，因为在初始投资建设微电网需要花费较多成本，并在后续过程因运维和环境维护产生额外成本。故在综合效益中综合考虑了经济性和环保性：

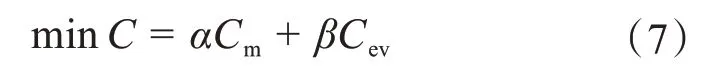
式中，C表示微电网的综合效益；α和β分别指上述的设备运行成本和环境影响成本所占比例。本文中认为运行成本和环境成本有着相同的考量权重，故两者的权重系数为0.5。

2.2 约束条件

（1）功率平衡约束

功率平衡表示微电网系统运行时，功率的生产和负载消耗要保持动态平衡，即输出功率等于输入功率，从而保证电能质量。

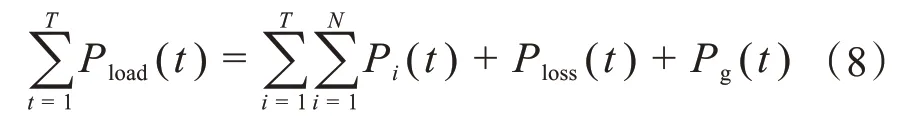
其中，Pload(t)为系统负荷在t时所需功率；Pi(t)为系统第i个发电源在运行t时后的有功功率；Ploss(t)为系统在运行t时后的损失功率；Pg(t)为系统与电网间的交换功率。

（2）电源输出功率约束

在微电网中配置的分布式电源，由于自身的物理特性的限制和外在因素的影响，可输出功率存在最大值和最小值。

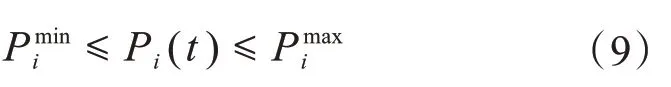
其中，Pmaxi、Pmini分别为系统中各功率输出单元能输出的最大、最小有功功率。

（3）电网功率交换约束

当微电网中各源、荷单位不满足电力系统供需关系时，微电网需要并网运行，从电网中交换能量以保证电网稳定。微电网和电网之间必定存在功率的交互。

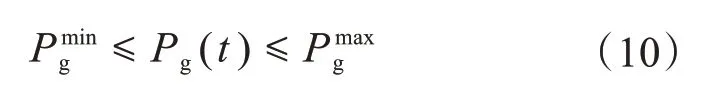
其中，Pming为微电网并网运行时交换功率的最小值，是微电网并网运行时交换功率的最大值；Pg(t)为两系统在一定时间内的交换功率。

（4）储能装置容量约束

本研究的微电网中储能装置配备的是蓄电池，因此其须满足蓄电池的充放电限制和容量的限制条件：

式中，Pdis(t)为选取的蓄电池放电功率；Pcha(t)为选取的蓄电池充电功率；Pmaxdis为配置的储能蓄电池最大的放电功率；Pmaxcha为配置的储能蓄电池最大的充电功率；SOC(t)变化值是蓄电池的容量状态通常在0-1间浮动，0代表储能电量完全放空，1代表是储能电量满额；其中SOCmin是蓄电池电能设定最小存储量，SOCmax是蓄电池电能设定最大存储量。

3 仿真分析

3.1 参数设置

微电网系统中，与运行条件和成本计算相关的设备参数如表1～表2所示。

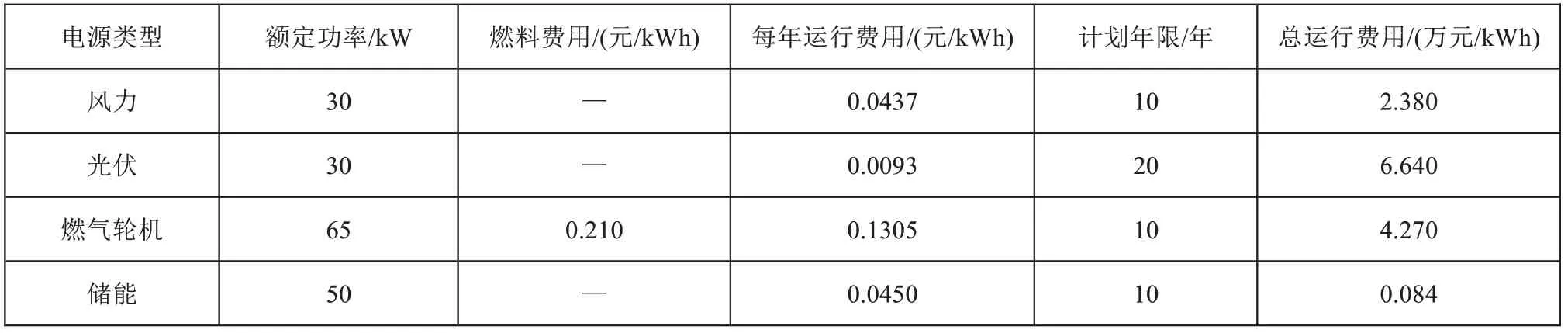
表1 各电源相关参数

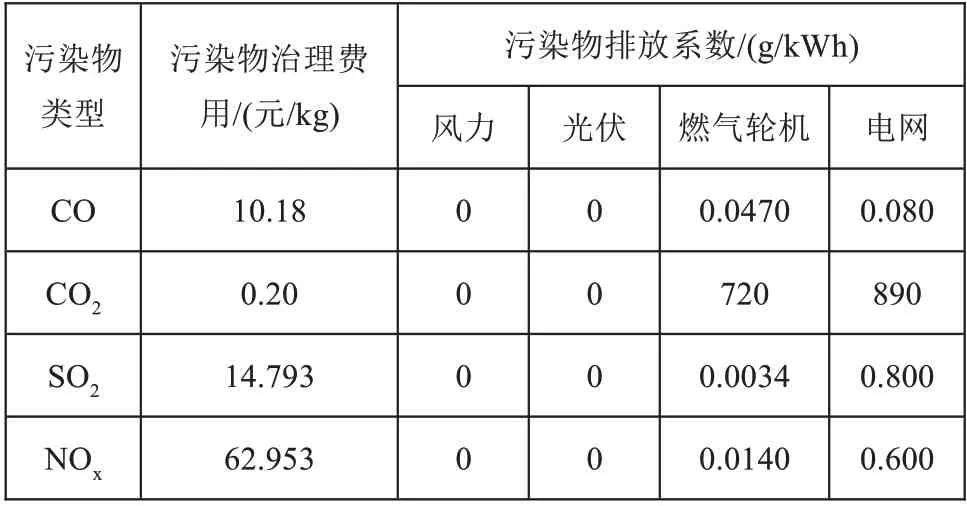
表2 各电源污染物排放系数

在该场景下，采用固定购售电价形式，并且电网和微电网可进行能量交换即为并网条件。故在向电网购电时，固定电价为0.5(元/kWh)，在向电网售电时，固定电价为0.39(元/kWh)。在该场景中，当微电网总输出的发电功率满足并超过负荷需求时，将多余的电量存储在蓄电池中。储能设备的荷电状态大于0.8时，系统就可将剩余电能以固定电价出售给大电力系统。

3.2 仿真分析

依据上述参数设置以及选取某地区夏季一日负荷变化曲线和风光电出力进行调度的仿真。在该场景下，光伏和风电的出力处于满发状态，优先满足微电网系统中的符合能量需求。当具有不确定性的风光出力不满足负荷时，燃气轮机为微电网持续提供电能。在该仿真条件下，燃气轮机一直在出力，当主发电单元仍有功率不平衡或不满足约束条件时，储能系统和电网交互作用得以显现。其作用一是避免能量浪费，可消解弃风和弃光量；二是售电行为可降低成本；三是增强主网和微电网的稳定性，削减不确定风光出力的直接影响。

4 结语

该方法能够对微电网各目标依据条件进行有效调度，具备快速求解调度问题的能力，同时避免了陷入局部最优解的困境，能够适配并解决在微电网场景下的调度问题。调度求解结果显示，微电网可避免能量浪费，消解弃风和弃光量，降低成本，增强主网和微电网的稳定性，削减不确定风光出力的直接影响。