基于深度强化学习的拉索智能减振算法

陈孝聪， 张恩启， 程 斌， 王 浩

(1.上海交通大学 船舶海洋与建筑工程学院，上海 200240；2.东南大学 土木工程学院，南京 210096)

拉索作为斜拉桥的重要受力构件，具有质量轻、阻尼小和柔度大的特征，易在外部激励荷载作用下发生不同类型的大幅振动，从而引起拉索锚固端产生疲劳裂纹，降低拉索的使用性能和寿命。在工程应用中多采用被动黏滞阻尼器来抑制拉索的大幅振动，但黏滞阻尼器能提供的最大模态阻尼较为固定[1]，且受阻尼器安装高度限制难以有效控制超长斜拉索的振动。一般可采用惯质阻尼器[2-4]、MR阻尼器[5-6]等取代黏滞阻尼器，并对拉索进行多模态振动控制。其中MR阻尼器具有可变阻尼的特性，已有研究表明[7]利用MR阻尼器进行半主动控制可获得比最优黏滞阻尼器更好的控制效果，且比拉索主动控制的输入能量更低。

MR阻尼器的减振控制效果与拉索振动频率、振动幅度、阻尼器施加电压、荷载作用形式等因素都有关[8-9]，半主动控制算法直接决定其控制效果。为此，国内外学者已针对拉索半主动控制算法开展了大量的研究，Johnson等提出了剪切最优H2/LQG算法，采用两级控制器实现了从LQG主动控制到半主动控制的转变。李惠等[10]利用LQG主动控制和限界Hrovat控制算法确定磁流变阻尼器控制力，基本实现了主动控制达到的效果。Weber F等[11]提出了基于调幅LQR控制的近似同位控制策略，通过对主动控制力特性的近似等效实现对拉索的多模态振动控制。Chen等[12]基于LQG控制实现了对自感应MR阻尼器的半主动控制。Zhao等[13]提出了基于LQR控制的最优等效控制算法，利用等效刚度和等效阻尼近似得到最优控制力，从而提高计算效率。以上控制策略以主动控制算法如LQR或LQG为基础计算最优控制力，一般需要对拉索-阻尼器系统振动特性建立精确的动力学模型和系统状态空间方程[14]，且需要根据有限数量的传感器测量值对拉索振动状态得到准确估计，从而获得有效的反馈增益矩阵进行动力学求解。

为了使振动控制策略更容易实施，需降低对精确数学模型的依赖性，并根据有限实时测量值进行在线反馈控制。对此邬喆华等[15]提出了基于位移和速度方向的Bang-Bang控制算法，根据阻尼器活塞位移和速度方向来实现半主动控制，但该算法存在阻尼器型号的有效区间。Zhou等[16]提出了仅利用阻尼器活塞位移和速度信息的调制均匀摩擦算法，但控制器增益值需要由结构参数分析确定。Liu等[17]提出了仅利用阻尼器活塞加速度信息的积分加二重积分控制算法，实现了对拉索的无模型同位控制。

本文采用基于深度强化学习的振动控制算法实现对拉索-阻尼器系统的无模型控制，即控制策略无需基于被控系统的精确数学模型，仅通过对系统的部分状态观测直接得到最优控制动作，从而实现端到端的在线控制。通过数值仿真方法建立斜拉索-阻尼器环境模型与控制算法进行交互，并考虑斜拉索的随机风荷载作用场景，将该算法的振动控制效果与黏滞阻尼器最优被动控制、Bang-Bang经典控制等进行对比分析，验证控制算法的有效性。

1 拉索-阻尼器环境模型

本文主要针对拉索的平面内振动进行控制，并考虑拉索垂度和抗弯刚度的影响，拉索-阻尼器系统计算模型如图1所示。

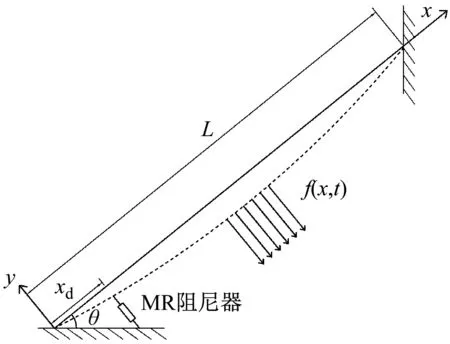
图1 拉索-阻尼器系统计算模型

拉索在横向荷载作用下的无量纲动力学方程可以表示为

(1)

(2)

式中：t代表振动时长；m代表拉索单位长度质量；T代表拉索静态张力；L代表拉索的总长度；w0代表拉索基频。动力学方程中拉索振动响应可以采用Galerkin方法求解，将拉索y向振动位移表示振型函数的组合形式，并需满足边界条件，即

(3)

φj(0)=φj(1)=0

(4)

式中：qj(t)为第j阶模态的广义位移坐标；φj(x)表示第j阶模态的形函数。为了减少计算所需模态数量，提高振动响应的求解效率，引入“0阶”振动模态，以静力状态下的位形作为形函数，即所有形函数为

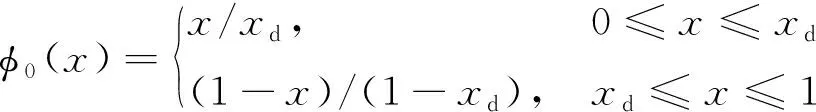
φj(x)=sin(jπx),j=1,2,…,n-1

(5)

由于拉索的各阶模态振型正交，因此可得振动方程的矩阵形式

(6)

φ(xd)|=|[φ0(xd),φ1(xd),φ2(xd),…,φn(xd)]T

(7)

质量矩阵M、刚度矩阵K、阻尼矩阵C、荷载矩阵Fy对应的元素可以表示为

(8)

2 深度强化学习控制算法

强化学习是一种通过智能体与环境进行交互得到最优决策序列的计算方法。智能体负责选择控制动作和改进控制策略，是运行强化学习算法的主体；环境即智能体所处的场景，环境会根据智能体的动作进行状态转换，并量化评价智能体的动作[18]。在拉索减振应用中，智能体为强化学习控制算法，环境模型为拉索-阻尼器被控系统。

在控制过程中，智能体感知到环境模型当前状态si，根据控制策略π(a|s)选择动作ai作用于环境，使环境模型从si进入到下一状态si+1，环境根据奖励函数R(s)评估si+1的优劣，并给予智能体回报ri+1。该过程将一直迭代循环，形成一条如s0,a0,r1,s1,a1,r2,s2,…的状态-动作-奖励序列。智能体通过最大化总体收益来优化控制策略，该收益不但包括当前时刻的即时回报，也包括后续序列的延迟回报，从而使智能体做出更有远见的决策。智能体在t步所获得的整体收益Gt可以表示为时间折扣因子γ与后续单步回报的组合，γ值的大小取决于其对未来收益的关心程度，γ=0表示只关注当前步的回报，γ=1表示关注未来所有步的回报。整体收益公式为

(9)

大部分强化学习算法都涉及到价值函数的迭代计算，价值函数可以用来评价智能体策略在给定状态下的优劣程度。Q学习算法为一种基于价值迭代的控制算法，其采用动作价值函数Q(s,a)描述状态s下选择动作a的价值，该函数由贝尔曼最优方程计算

Q(st,at)=

(10)

采用时序差分法来更新当前时刻的动作价值

Q(st,at)=Q(st,at)+αδt

(11)

式中，α为步长参数，δt为时间差分值，即

(12)

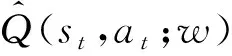
(13)

除了采用参数化函数降低状态空间的复杂性，DQN算法也通过经验回放池随机采样减少了对样本序列的依赖，且通过固定目标DQN网络提高了算法的收敛性和稳定性。在公式(13)表示的算法基础上，研究人员提出了Double DQN[20]和Dueling DQN[21]的优化方法。Double DQN采用两个参数不同的DQN网络分别负责动作选择和策略评估，解决了值函数估计的误差问题，其动作价值函数可以表示为

(14)

Dueling DQN利用状态价值函数V(s;w,α)和动作优势函数A(s,a;w,β)的组合，加速智能体学习最优控制策略的过程，其中α,β都为近似函数参数集合，则动作状态价值函数可以表示为

(15)

本文将经过Double DQN和Dueling DQN技术优化后的DQN控制算法应用于拉索振动控制场景，整体控制框架如图2所示。智能体根据拉索振动状态有限观测值st-1采用ε-贪心方法选择MR阻尼器施加电压a，拉索在外部荷载ft和阻尼力作用下更新状态至st，根据奖励函数R(st)产生回报rt。

上述交互过程会产生一个包含状态、动作和收益的样本(st-1,a,st,rt)，并将其存入经验回放池。其中，状态st采用t时刻阻尼器作用点位置的瞬时位移、速度、加速度值。a为离散动作空间内的电压值，取MR阻尼器最大控制电压10 V，电压离散点间隔为0.5 V。为降低测量要求，并尽量捕捉拉索振动状态，算法分别取L/4、L/2、3L/4位置的瞬时位移、速度值计算单步收益rt，且均方值越小，回报越大，因此回报函数可以设置为

(16)

式中，k1和k2分别为权重系数，可根据控制目标设定。

当经验回放池达到一定规模时，算法将随机采取定量样本训练内部Dueling DQN网络，样本数量根据参数分析结果确定。利用网络输出结果计算时序差分值δt，以梯度下降法更新神经网络权重等参数，最终使智能体达到最佳决策状态。此外，控制框架将智能体输出决策和训练神经网络设置为异步程序，从而满足实时计算效率要求。

图2 深度强化学习振动控制框架

3 算例与结果分析

3.1 仿真对象参数

本算例选取岳阳洞庭湖大桥A11斜拉索作为仿真对象[22]，如图3所示。拉索主要参数为：索长114.72 m，设计索力为3 095 kN，单位长度质量为51.8 kg/m，拉索直径为119 mm，斜拉索倾角为37°，由理论计算得到的前三阶模态频率分别为为1.06 Hz、2.13 Hz、3.20 Hz。仿真时阻尼器安装位置距拉索下锚固端距离为斜拉索长度的2%。

图3 洞庭湖桥A11斜拉索及3号节点位置

3.2 风荷载模拟

本算例采用拉索的风致振动响应来验证控制算法的有效性。风荷载可以表示为平均风压和脉动风压之和，在振动控制研究中仅考虑脉动风压的作用，一般将脉动风假设为平稳高斯随机过程，并可通过线性滤波法或谐波合成法进行模拟。本文将采用谐波合成法进行风荷载的模拟，取Davenport谱作为脉动风功率目标谱，取地面粗糙度指数为0.1，取桥面距地面高度为52 m，所在场地20 m高度处的标准设计风速V20为28 m/s，截止频率为10π，卡门常数为0.4，地面粗糙长度为0.03，频率点数取4 096个。沿A11斜拉索从下至上选取均匀分布的40个节点并进行编号，如图3所示。通过模拟计算可得到每个节点的瞬时风速时程曲线，其中3号节点的瞬时风速时程曲线如图4所示。图5给出了3号节点脉动风模拟功率谱和目标功率谱，结果说明两者能量分布吻合性较好，验证了风速时程模拟的精度。

图4 3号节点瞬时风速时程

图5 3号节点风速功率谱与目标功率谱

基于模拟的风速，作用于拉索的风荷载可由下式计算[23]

(17)

式中：ρ为空气密度(取1.23 kg/m3)；v(z,t)为节点瞬时风速；CH为风阻系数(取0.7)；D为拉索等效直径；θ为拉索倾斜角。

3.3 阻尼器参数模型

α(u)=αa+αbu

c0(u)=c0a+c0b

c1(u)=c1a+c1bu

(18)

式中：z,y为内变量；k1为蓄能器刚度；c0为高速率时的黏滞阻尼系数；c1为低速率时的黏滞阻尼系数；k0为高速率时的等效刚度；x0为蓄能器的初始位移；α,β,γ,A为描述阻尼力-速度曲线中线性段和屈服渐变段的关键参数。

取已在洞庭湖拉索减振研究中应用的RD-1005型阻尼器作为作动器，并采用Liao等[25]对该阻尼器现象模型参数的辨识结果进行数值模拟，参数如表1所示。

表1 RD-1005型MR阻尼器现象模型参数

3.4 仿真结果分析

本算例采用Newmark-β算法对拉索的风致振动响应进行求解，取关键计算参数α=0.5，β=0.25，以保证算法的收敛性。取动力仿真时长为160 s，其中拉索风致振动时长为100 s，自由振动时长为60 s。仿真步长Δt=0.02 s，在每个仿真步长内设定最大迭代子步数为30，并设定精度限值，当达到最大迭代步数或满足精度要求时则退出循环。考虑前10阶振动模态，利用Galerkin法计算拉索风致动力响应，为使振动控制效果更突出，对风荷载予以一定程度放大。

以无控制下的拉索振动响应为参考进行标准化处理，表2对比了全仿真时长160 s内拉索在四种控制策略下的位移、速度、加速度响应的均方根和最大值。结果表明，在随机风荷载作用下，VD多模态控制、Bang-Bang控制、深度强化学习控制策略均能实现有效减振。与无控制工况对比，深度强化学习控制下的位移、速度、加速度响应的最大值分别降低了4.79%，37.3%，52.8%，均方根分别降低了46.9%，62.4%，69.7%。与VD多模态控制相比，深度强化学习控制下的位移、速度响应的最大值分别降低了1.08%，2.52%，加速度响应最大值则略差于被动控制，三种响应的均方根分别降低了9.68%，11.09%，3.41%。与Bang-Bang经典控制相比，深度强化学习控制在位移、速度和加速度响应的最大值分别降低了3.15%，3.52%，26.7%，均方根分别降低了4.29%，5.62%，8.56%。综合以上分析结果可以得出，深度强化学习控制策略的减振效果总体优于VD多模态控制和Bang-Bang控制。且相较于加速度响应，该控制策略在速度和位移响应上的减振优势更显著，这与奖励函数的特性有关。智能体为取得最大收益，更倾向于使拉索维持在位移、速度均方根值小的低能量状态，而主动调节阻尼器电压会提高局部加速度响应，这也解释了深度强化学习控制下的拉索加速度幅值略高于最优被动控制的现象。

表2 不同控制策略下拉索的标准化振动响应对比

取拉索跨中位置在80～120 s的振动响应对不同算法控制效果进行可视化分析，如图6所示。结果表明，基于深度强化学习的半主动控制策略要优于VD多模态控制和Bang-Bang控制。其中位移和速度响应的优化效果较为明显，加速度响应的稳定性略差于最优被动控制，与前述分析结果一致。

图7为全仿真时长内拉索全长的振动响应轮廓线。结果表明，深度强化学习控制算法对应的位移轮廓和速度轮廓要优于其余两种控制策略，而加速度轮廓略差于VD多模态控制策略，优于Bang-Bang控制策略。由加速度响应轮廓可以看到Bang-Bang控制策略在阻尼器位置的加速度值较为突出，这是由于其控制律较为固定，只基于阻尼器活塞的相对速度和相对位移，没有对拉索状态的适应性调节，且容易受到测量误差的影响，因此容易造成局部区域的稳定性较差，而深度强化学习算法的控制效果更为稳定。

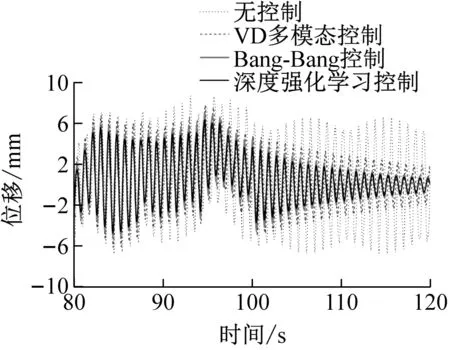
(a) 位移响应时程曲线对比

(a) 位移响应轮廓对比

4 结 论

本文提出了一种基于深度强化学习算法的拉索半主动自适应控制策略，利用优化后的DQN控制算法实现了对拉索振动的无模型控制。对比分析了VD多模态控制、MR阻尼器Bang-Bang控制、深度强化学习控制策略下的拉索风振控制效果，研究结论如下：

(1) 深度强化学习控制算法可实现对拉索风致振动的有效控制，且控制效果总体优于VD多模态控制和Bang-Bang控制，为拉索振动半主动控制提供了新的解决思路。

(2) 深度强化学习控制算法具有自适应特性，仅在特定位置点设置观测器即可实现拉索振动的在线控制，无需建立全状态反馈。此外，该算法能够实现从拉索振动状态到最优控制电压的直接决策，无需建立MR阻尼器逆模型进行控制力到电压的二次转换，从而控制策略更易实施。