基于变步长龙格库塔法的高炮C-RAM解命中方法

刘新宇，舒立鹏，林智伟，吴 晔，朱柏飞，唐 旭

(西北机电工程研究所， 陕西 咸阳 712099)

1 引言

C-RAM(counter-rocket artillery mortar)是一种使用我方防空火力主动拦截来袭的火箭弹、榴弹和迫击炮弹，以达到防御敌方地面曲射火力打击的主动防护系统[1]。高炮C-RAM火控系统的任务是根据雷达对来袭RAM目标的跟踪数据估计出其实时位置、速度并辨识其弹道系数，根据以上信息通过解命中计算得出目标的未来命中点并射击，从而实现对RAM目标的拦截。但在火控处理时，由于RAM目标的运动模式的非线性性[2]，传统的高炮解命中方法因假定模型以及计算方式的问题无法得到正确的解命中结果。由此需要设计一种基于RAM目标运动方程假定，通过积分方法计算未来点的高炮C-RAM解命中方法，以实现高炮C-RAM作战的需要。

2 RAM目标运动特性

由于在实际进行C-RAM作战时目标弹丸转速、攻角、弹翼升力等状态无法测得，这些状态对于弹丸运动轨迹在短时间内的影响较小，在进行短时间的外弹道外推时相对于弹道系数估计误差造成的未来点偏移其影响基本可以忽略不计，故本文采用弹丸质心运动模型作为外推RAM目标外弹道轨迹的公式，将除去空气阻力与重力外的其他力对弹丸运动的影响看作是弹道系数误差所造成的影响的一部分或是将其忽略。基于C-RAM作战时一般在RAM目标的外弹道末端进行拦截，此时目标速度通常处于亚音速状态，弹道系数值的变化幅度较小，故可以将弹道系数视为常值进行处理，并假设气象条件是标准的，无风雨干扰。弹丸质心运动模型示意图如图1。

图1 弹丸质心运动模型示意图

弹丸质心运动方程组如式(1)所示:

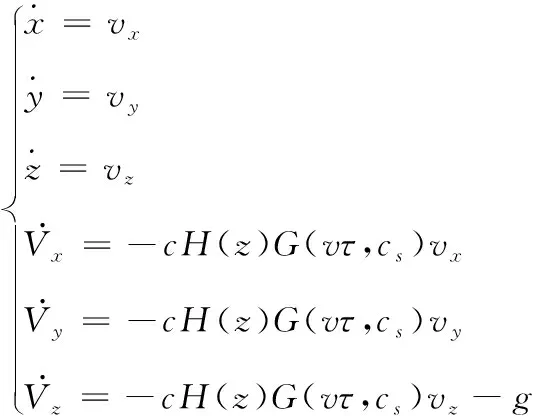
(1)

式中:x、y、z、vx、vy、vz分别为弹丸的位置坐标与速度分量;c为弹道系数；g为重力加速度；cs为声速；H(z)为空气密度特征函数；G(v,cs)为空气阻力函数[5-7]。

3 RAM类目标火控解命中方法

3.1 龙格库塔默森法

(2)

其中：

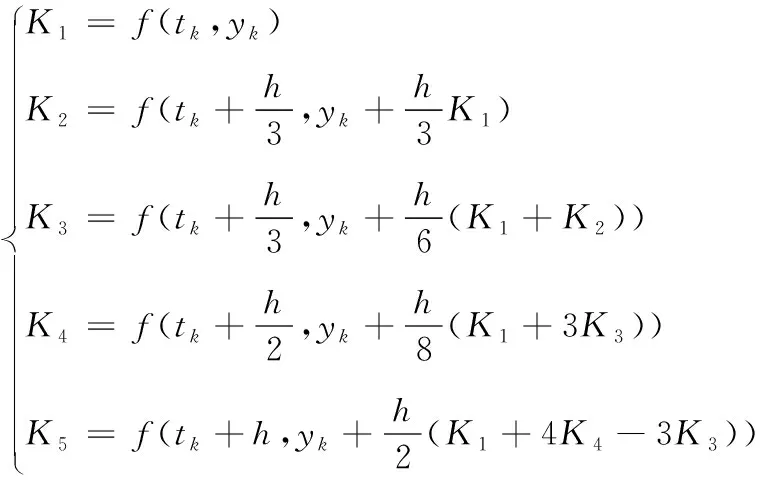
(3)

误差估计值计算公式如式(4)所示：

(4)

此误差估计值的精度为3阶，而此方法的积分精度为4阶，对于大部分使用情况已经能够满足精度要求。

3.2 命中方程求解方法

(5)

(6)

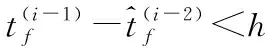
以上命中点积分方法使得在进行弹道外推时预测命中点不会超过实际命中点过多，从而最大程度上的减少积分次数。

3) 命中点水平距离和高度求解:

(7)

(8)

4) 弹丸飞行时间求解:

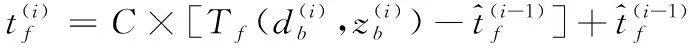
(9)

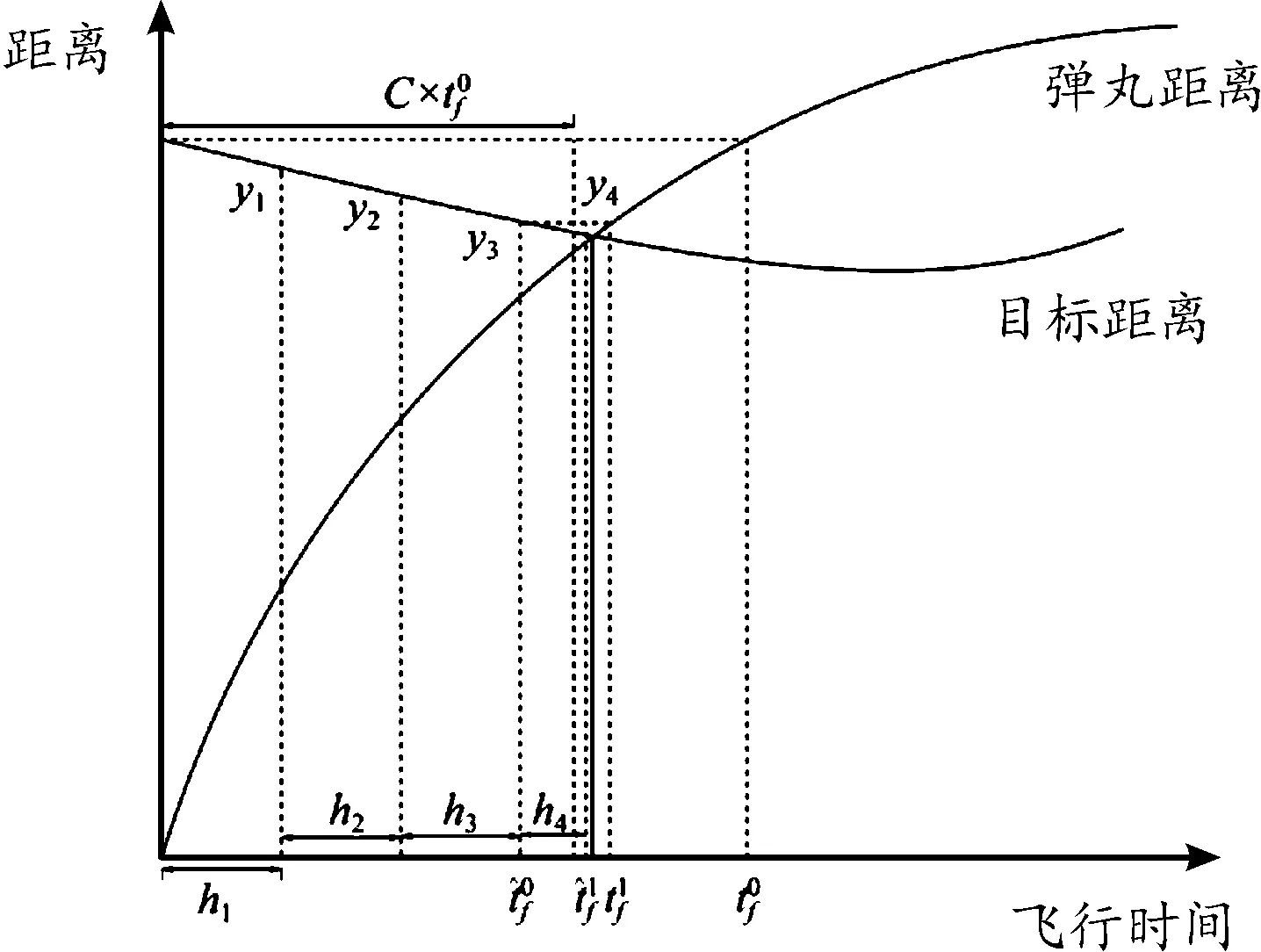
图2 结合龙格库塔积分方法的迭代法收敛曲线

3.3 固定步长龙格库塔默森法下积分误差估计值及诸元解算误差的统计经验

总结出以下结论：

1) 解命中误差与积分步长成正比；

2) 对于拥有同一初速度、速度方向、高度、弹道系数但高炮与弹丸轨迹水平投影斜距不同的弹道，解算误差除以弹丸飞行时间的值与积分步长为线性关系，且斜率相对一致；

3) 不同斜距的外弹道轨迹下，x轴与y轴位置坐标估计误差与积分步长的3次方的比值与积分步长为斜率相对一致的线性关系；

4) 不同斜距的外弹道轨迹下，z轴位置坐标估计误差与积分步长的2次方的比值与积分步长为斜率相对一致的线性关系；

5) 同一条弹道在进行误差估计时在在积分步长一致的情况下估计误差的变化较小。

各项结论所总结的关系如图3—图6所示。

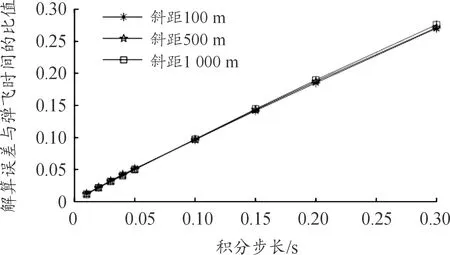
图3 x轴解算误差与弹飞时间的比值曲线

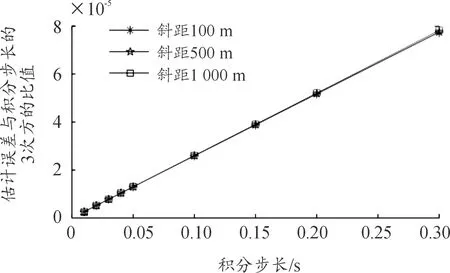
图4 x轴估计误差与步长3次方的比值曲线

图5 z轴估计误差除以步长2次方值的曲线

图6 同一弹道在定步长下不同次积分的估计误差变化

对不同弹道进行仿真后确认了以上统计经验具有广泛性，故可以将实际误差、误差估计值、积分步长之间的关系总结为如式(10)所示的公式。

(10)

式(10)中：Cx、Cy、Cz为各轴的误差换算比值常数；Ex、Ey、Ez为各轴位置估计误差；ht为积分步长；Ex_ture、Ey_ture、Ez_ture为实际位置解算误差；tf为弹丸飞行时间。

在对多种弹丸的弹道进行大量仿真验证后发现，在不同弹道系数及弹丸速度下，误差换算比值常数Cx、Cy、Cz是不同的。对一飞行轨迹起点固定的弹丸进行定步长解命中仿真，设定弹道系数为0.5，改变每次计算时x轴的初始速度，x轴误差换算比值常数随积分步长与x轴速度变化曲面如图7。积分步长为0.05 s时，x轴误差换算比值常数在不同弹道系数下随x轴速度变化的曲面如图8。

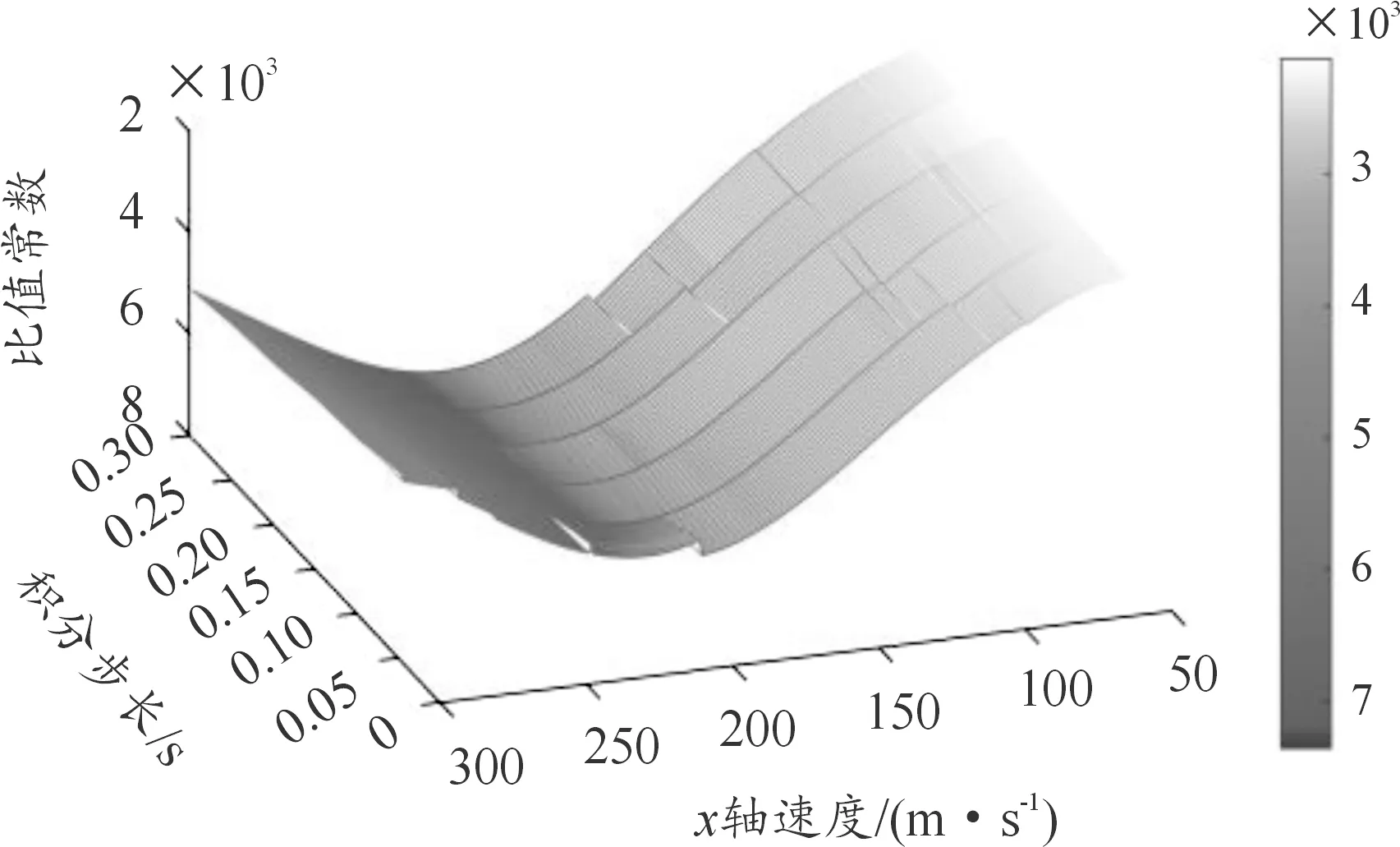
图7 不同速度、积分步长下的误差换算比值常数变化曲面

图8 不同速度、弹道系数下的误差换算比值常数变化曲面Fig.8 Variation curve of error conversion ratio constant under different speeds and ballistic coefficient

从图7、图8的结果中可以看出该比值常数在不同速度以及弹道系数下是不同的，变化规律也呈非线性，但不随积分步长变化。在使用式(10)估计实际解算误差时，比值常数的取值将决定估计出的实际解算误差准确与否。

对于比值常数的取值问题，在实际应用时的解决方式有3种：

1) 通过大量的实验来制作对应不同弹道系数、速度的比值常数表，在计算时根据目标的弹道系数以及速度从表中取值；

2) 将比值变化曲线近似线性化，在计算时根据近似函数得出比值用于计算；

3) 取一固定值，保证大部分高概率情况的解算效果，牺牲小部分低概率情况的解算精度和速度。

(11)

其中：

(12)

其误差估计值计算公式如式(13)所示：

(13)

夏普法中K5正好是下一次积分计算时的K1，因此只需要在第一步多算一次K1，之后每步积分只需要计算4次右端函数。其误差换算公式如式(14)所示，形式与默森法基本相同，但积分步长次方值不同。

(14)

根据式(14)计算出的夏普法误差换算比值常数变化曲面如图9、图10。可以看出相比于默森法的比值常数变化曲线，夏普法的比值常数在速度和弹道系数较大时，同一速度、弹道系数下其不同积分步长对应比值常数变化较大。故在速度和弹道系数较大的情况下，若要进行最优步长控制，夏普法的步长控制难度要大于默森法，故相比于默森法，夏普法并不适用于C-RAM的解命中计算。

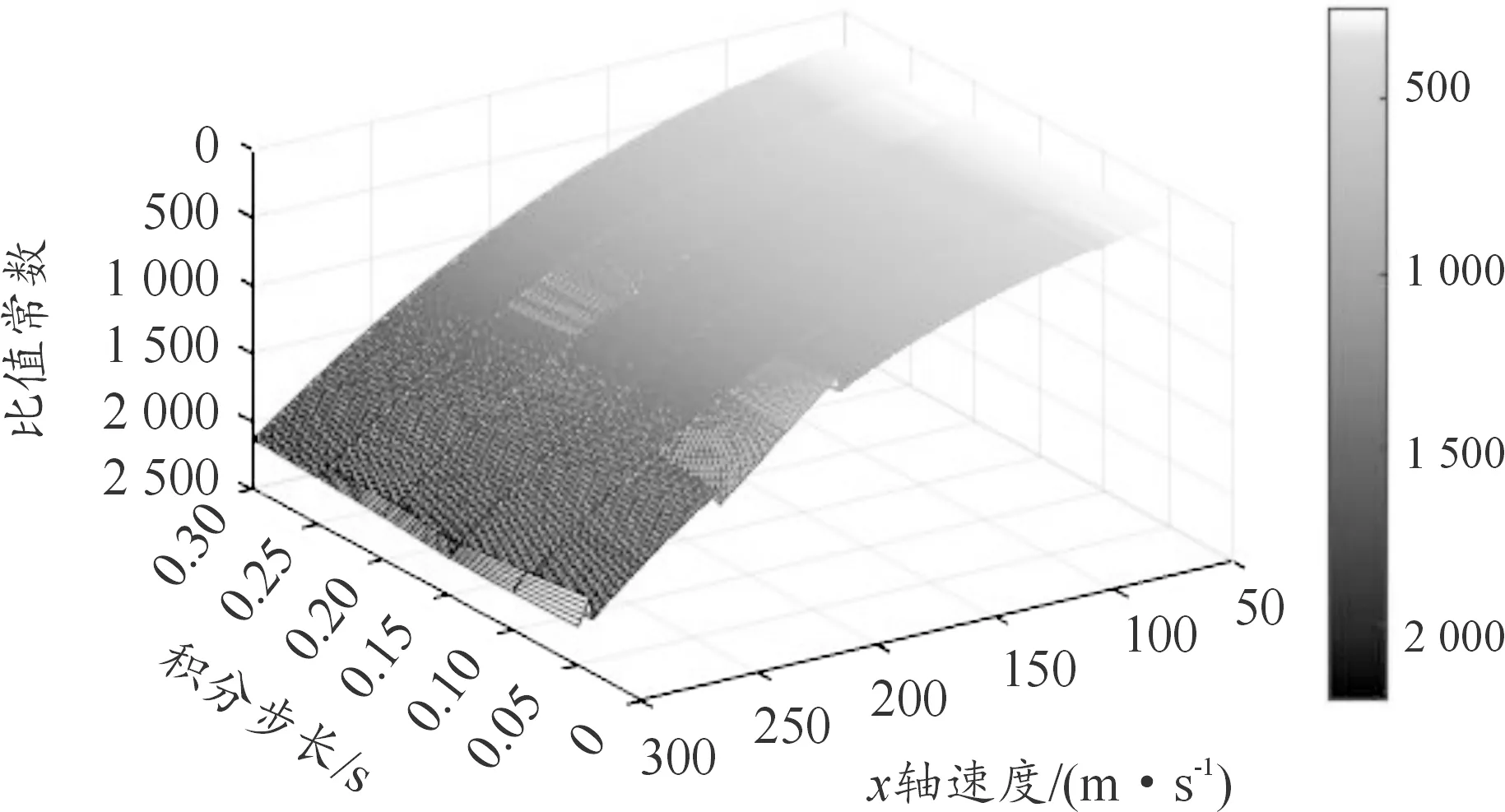
图9 弹道系数=0.2，不同速度、积分步长下夏普法的误差换算比值常数变化曲面

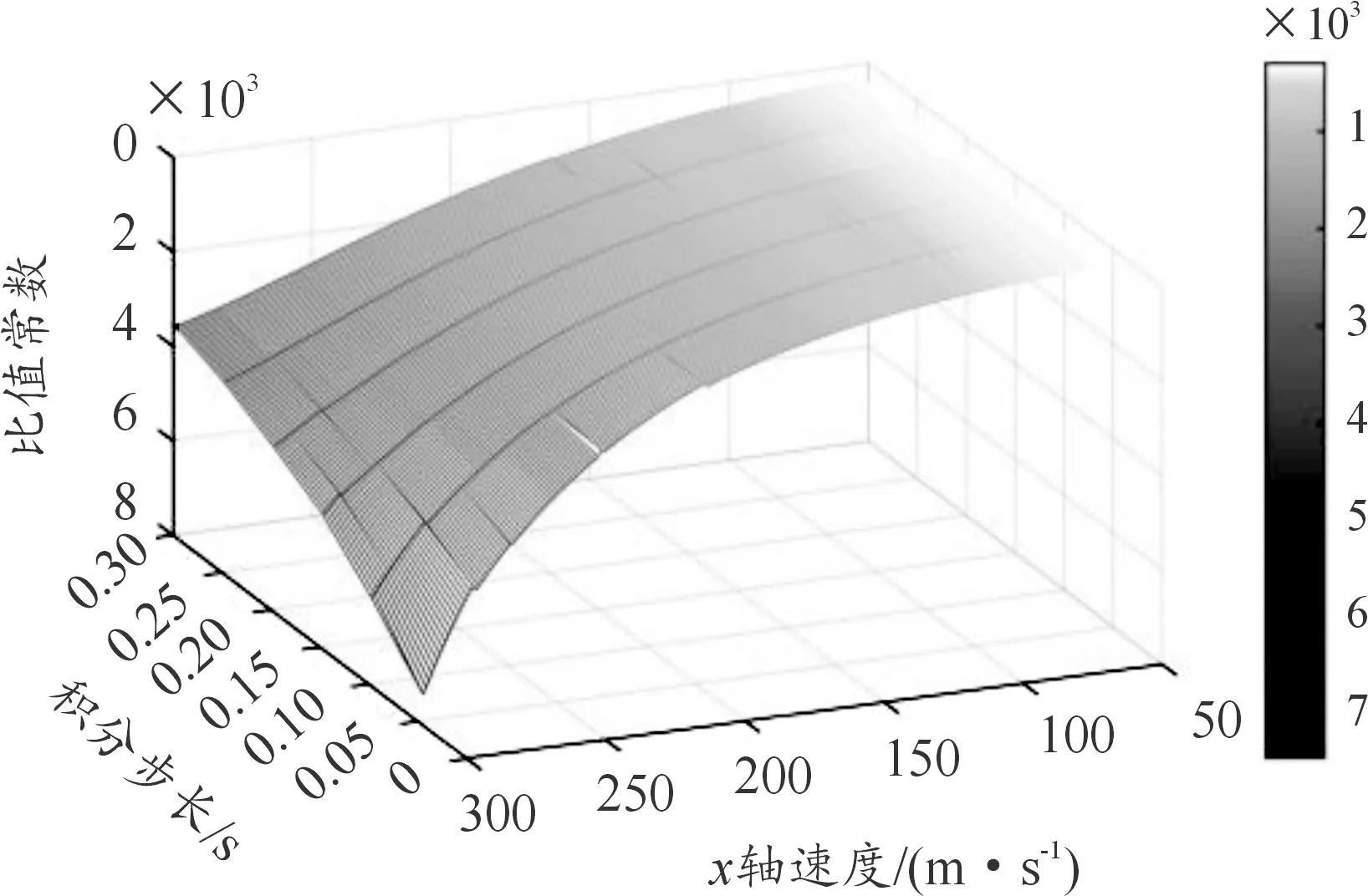
图10 弹道系数=0.5，不同速度、积分步长下夏普法的误差换算比值常数变化曲面

3.4 基于最优步长控制策略的龙格库塔默森法

具体的最优步长控制策略为：

① 首先以一较为合适的固定步长hm进行第一次解命中，求得弹丸飞行时间tf。

② 给定误差限制ε0，以固定步长hm作为第一次积分步长，以上一次解命中的弹飞时间tf作为本次解算参考弹飞时间，求若以本次积分步长进行解命中时各轴诸元解算的误差值εx、εy、εz，公式为式(15)所示。

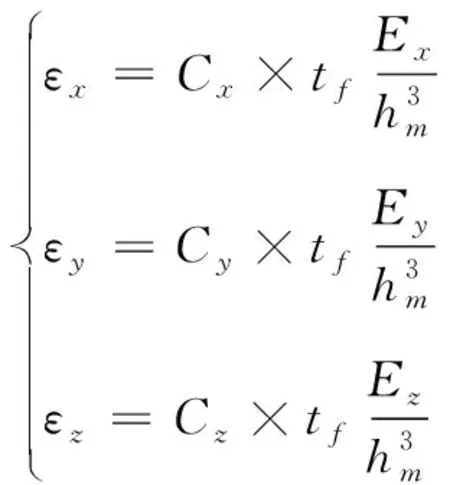
(15)

若εx≤ε0且εy≤ε0且εz≤ε0，则本次积分成功，通过式(16)确定下一步步长hm+1。

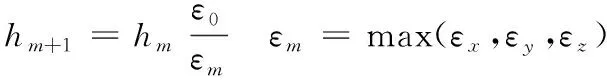
(16)

若εx>ε0或εy>ε0或εz>ε0，则本次积分误差过大，同样通过式(16)求出一个积分步长hm+1。为了尽量不重复进行积分运算，减小计算时间，在一次诸元解算中除第一次积分外均无需重新积分。在同一次解算中同一积分步长造成的误差相差不大，除第一次积分外若出现计算误差值大于误差限制值的情况，只需要减小下一次积分步长保证下一次积分的精度即可。若对解算精度的要求较高，则只需要将误差限制值设置的比理想误差值稍小就能控制每步积分的误差在范围内。

③设置最小步长hmin，一旦积分步长小于此步长值则不再适用步长控制，此举是为了避免计算机在步长过小时由于舍入误差造成数值偏差比过大，从而计算出一个过大的误差值，引起步长振荡导致解算失败。

4 实例仿真

为验证基于统计特征的最优步长控制策略是否能够有效控制积分步长使解命中误差保持在可接受范围，对某2个RAM目标进行解命中计算，假设目标一被探测到时的弹道起点为x=500 m、y=1 000 m、z=1 000 m,高炮位于坐标原点，弹丸速度向量为x轴方向-250 m/s、y轴方向-250 m/s、z轴方向-90 m/s，弹道系数为0.2。

目标二被探测到时的弹道起点为x=500 m、y=1 000 m、z=1 500 m,高炮位于坐标原点，弹丸速度向量为x轴方向-200 m/s、y轴方向-150 m/s、z轴方向-150 m/s，弹道系数为0.3。

假设解命中过程中所得到的目标运动状态以及弹道系数均为理想值，每次诸元解算间隔为0.01 s，共解算600次。基于变步长默森法的解命中法为方法一，基于变步长夏普法的解命中法为方法2，文献[2]中的定步长解命中法为方法3，变步长法设置误差限制为各轴位置误差小于0.1 m，方法1比值常数取值为Cx=Cy=14 000、Cz=110；方法2比值常数取值为Cx=Cy=2 200、Cz=20；定步长法设置积分步长为0.05 s。

分别使用3种解命中方法对目标一及目标二进行仿真。诸元解算后进行逆解得到的解算误差如图11—图13所示。

图11 x轴位置解算误差图

图12 y轴位置解算误差图

图13 z轴位置解算误差图

从仿真结果中可以看出，相对于定步长的C-RAM解命中的方法，变步长法能够使各轴方向上的解算误差基本保持在设定的误差范围内。但由于比值常数使用了取固定值的方法，导致对误差的控制精度较差，解算误差超出设置范围的情况，若是采取使用比值常数表或者拟合比值变化曲线的方法，将能进一步的提升误差控制的精度。

在变步长法中，相比默森法的误差控制效果，夏普法在对目标一解命中时效果与默森法接近，对目标二解命中时误差小于默森法。但误差较小并不意味着控制效果好，夏普法与默森法的积分精度同为四阶且误差估计精度也同为三阶，在相同的精度条件下，更小的解算误差代表消耗了更多的解算时间，证明了在积分步长控制效果上夏普法要弱于默森法。且仿真中发现对夏普法应用本文中的最优步长控制时不能将上一次计算出的K5代入下一次计算中，否则将会因为步长的变化导致误差估计值的计算出现错误，进而无法有效控制积分步长，故在每步计算量上夏普法与默森法也基本相同，使其不具备计算量的优势。

变步长默森法积分步长的控制效果如图14、图15所示。

图15 变步长法解算目标二时积分步长控制云图

由图14、图15所展示的积分步长控制情况中可以看出，本文中的变步长C-RAM解命中方法能够实现对积分步长的最优控制。其能够实时的调节积分步长的大小，在积分误差较大的情况下减小步长保证精度，积分误差较小时增加步长减少积分次数。实现在保证解命中精度的情况下尽可能增加积分步长的长度，减少计算时间。

5 结论

1) 在基于弹丸质心运动模型模拟理想RAM目标外弹道轨迹的情况下，基于变步长龙格库塔法的高炮C-RAM解命中方法可以完成高炮C-RAM解命中任务。

2) 基于C-RAM解命中误差与积分估计误差规律应用的最优步长控制策略能够完成对积分步长的最优控制，相比使用定步长积分法进行C-RAM解命中计算，该方法可控制目标在不同距离、速度、弹道系数情况下的诸元解算误差。

3) 在同样应用最优步长控制方法同样精度的变步长积分法中，默森法相比于夏普法步长控制效果更好，更适合用于C-RAM解命中计算。

若能够在工程应用方面解决误差换算比值常数表的编制问题，则该方法便可以工程化应用于高炮防空系统中，可提高高炮的C-RAM作战能力。