碳纤维单向层合板落锤冲击损伤特性试验与仿真研究

刘 峰，张梦涛，王卓煜

(中国民用航空飞行学院, 四川 广汉 618307)

1 引言

碳纤维层合板因其较高的比刚度和比强度、可设计性强等特性，广泛应用于航空航天领域。碳纤维层合板易受鸟类、冰雹、掉落维修工具等外物的冲击[1-2]。Prasad和Hou[3-4]等研究了冲击头形状和材料对复合材料性能的影响，结果表明：冲击头的形状对性能影响较小；相同冲击能量下，层合板的损伤面积随冲头材料硬度增大而增大。孙子恒等[5]对不同铺层方案的碳纤维层合板进行了冲击试验，发现不同铺层方案碳纤维层合板的损伤面积、冲击力曲线差异很大。以上学者都通过试验研究复合材料的冲击性能，未对损伤与冲击性能之间的关系进行分析。许多学者采用试验与仿真相结合的方法对复合材料损伤进行分析，且已经取得了一定进展[6-8]。肖琳[9]通过4组低能量冲击试验，研究了冲击过程中层合板的应变历程，建立有限元模型分析了冲击过程，并与试验结果进行了对比，分析了合板的损伤机理。段苗苗等[10]建立了层合板的三维模型，对层内失效和层间损伤进行了仿真，讨论了层合板内部损伤的产生和演化过程。以上学者研究复合材料损伤机理时均采用参数折减方式对失效单元的刚度进行折减，折减系数需多次试凑，不符合实际物理过程中刚度线性或非线性衰减的情况[11]。

本文以T300 12K/164型单向带碳纤维增强树脂基复合材料的冲击性能和损伤机理为研究对象，开展了冲击性能试验。建立了非线性有限元冲击模型，对冲击过程进行数值仿真。将计算结果与试验结果进行了对比，分析了碳纤维层合板的非线性损伤机理，对损伤过程进行描述，研究了损伤与冲击性能的关系。

2 试验方法

2.1 试验材料

采用东丽公司生产的T300/12K碳纤维单向布作为增强材料，国产164环氧树脂作为基体。采用湿法施工方式，真空加压至0.91 bar，常温固化8 h制作碳纤维层合板。通过试验测得材料参数，如表1所示。由于工艺原因，相较预浸料热压罐工艺的试件，成品力学性能较低，但成本低廉，试件生产周期短。

表1 碳纤维复合材料性能参数

其中Eii(i=1,2,3)为弹性模量，Gij为剪切模量，Sij为剪切强度，μij(i,j=1,2,3,i≠j)为泊松比，Xt、Yt、Zt为材料各方向的拉伸强度；Xc、Yc、Zc材料各方向的压缩强度,Gft、Gmt为为纤维和基体拉伸破坏的断裂韧性，Gfc、Gmc分别为纤维和基体压缩破坏的断裂韧性[12]。

2.2 试件设计与制备

参照GB/T14153标准对试件进行设计，试件尺寸如图1所示，长度方向为材料主方向1方向。铺层方案为[0]8,厚度为2 mm。依据GB/T14153标准制取长为250 mm,宽为25 mm的试验样品。冲击点为试件的形心位置。

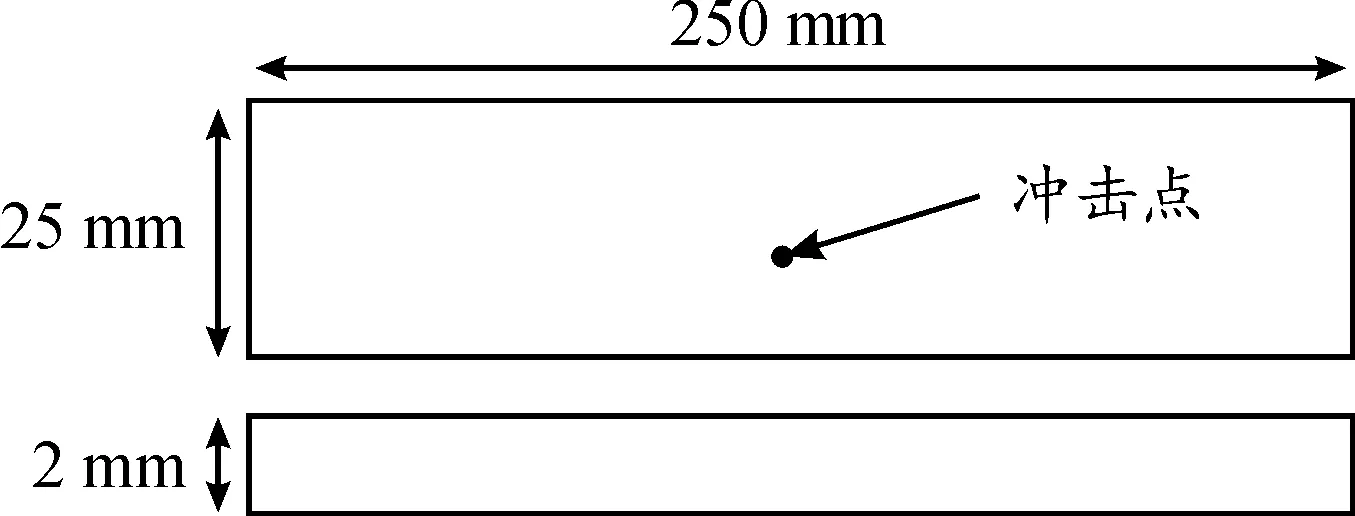
图1 试件示意图

2.3 试验仪器与方案

冲击试验参照GB/T14153标准,采用万测DIT152落锤冲击试验机进行试验。冲击头端部为半球形，直径16 mm，冲击组件总质量为5.5 kg。实验数据由NI USB-6351高速采集系统传输给计算机进行分析，得到冲击过程中的接触时间、位移、接触力等数据。使用OLYMPUS-SZX7体视显微镜对冲击后试验件表面的细观形貌进行拍摄，分析冲击区域的损伤形式和损伤机理。

冲击平台上放置一个刚性板，使用C形夹将试件固定在刚性板上，避免试件在受冲击时发生振动，减小试验系统的能量耗散，如图2和图3所示。选取不同的能量值开展冲击试验，试验矩阵元素如表2所示。

图2 试验装置示意图

图3 试件夹持方式示意图

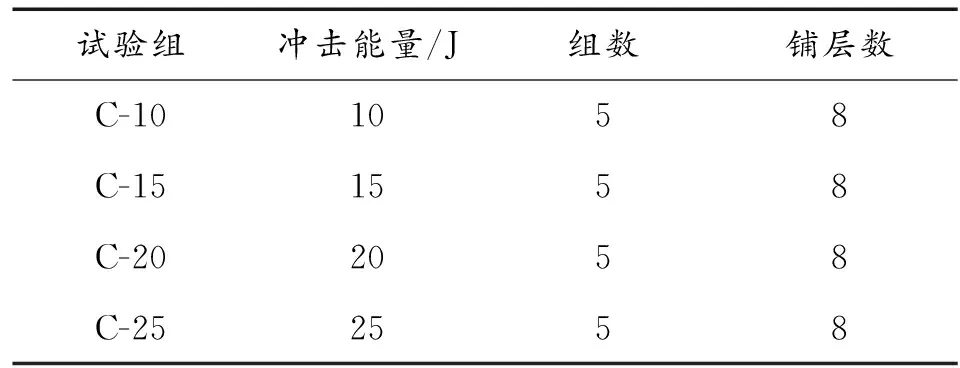
表2 试验矩阵元素

3 试验结果分析

3.1 不同能量下力-位移曲线

试件受到10 J能量冲击时的接触力-位移曲线如图4。图4曲线上标记的F0、F1、F2、F3、F4五个点依次代表原点、曲线斜率初始下降点、接触力峰值点、冲击头位移最大点以及冲击头位移终点。冲击头的接触力与碳纤维试件的刚度和强度有关。冲击载荷未达到破坏应力之前，接触力主要与刚度有关；超过破坏应力即进入渐进损伤过程后，损伤会造成刚度衰减，此时接触力主要与强度有关。从F0至0.1 mm位移之间处于初始接触阶段，结构接触刚度较低。0.1 mm位移至F1点之前处于等斜率线性阶段，表明此时试件基本未产生损伤，接触力主要与试件刚度有关，且随冲击头位移增大而增大。F1至F2点呈现非线性振荡特征，试件进入渐进损伤状态，接触力整体仍呈增大趋势。在F2点，接触力达到峰值。F2至F3点亦为非线性振荡状态，但冲击头接触力整体呈下降趋势，损伤进一步扩展，接触力随冲击头位移增大而减小。此过程中，冲击头处于减速阶段，减速原因来自两方面：一是试件损伤导致部分能量被试件吸收，二是试件中未破坏层板和刚性板的弹性变形起到了一定的缓冲作用。在F3点，冲击头速度为0，冲击头位移取得最大值1.29 mm。F3至F4点，刚性板和试件未破坏的层板弹性变形回复，导致冲击头位移减小，冲击头接触力迅速振荡下降，位移约为0.4 mm时冲击头与试件脱离接触，接触力降为0。

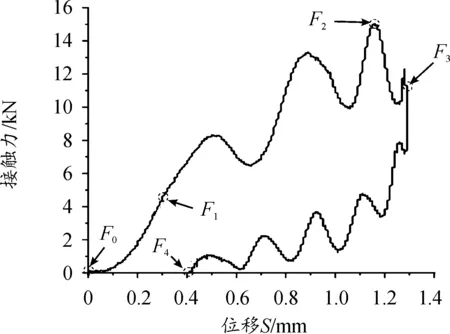
图4 C-10组接触力-位移曲线

试件受到10 J、15 J、20 J、25 J四种能量冲击时的接触力-位移曲线如图5。由图5可知，其他3组曲线趋势与C-10组基本一致。各试验组的冲击头接触力峰值依次为15.03 kN、16.54 kN、17.13 kN、16.33 kN，接触力峰值随冲击能量增大呈现出先增大后减小的趋势。4个试验组接触力峰值依次在1.16 mm、1.40 mm、1.52 mm、1.28 mm处取得，接触力峰值对应的冲击头位移随冲击能量增大呈先增大后减小的趋势。由于前3组试件的冲击能量相对较低，层合板损伤程度较轻，刚度衰减较小，使得接触力持续增加。C-25组试件的冲击能量较大，材料在高能量冲击下进入了更为严重的渐进损伤过程，出现明显的纤维断裂、基体开裂等损伤形式，局部刚度和承载能力下降，因此接触力曲线也出现整体下降。

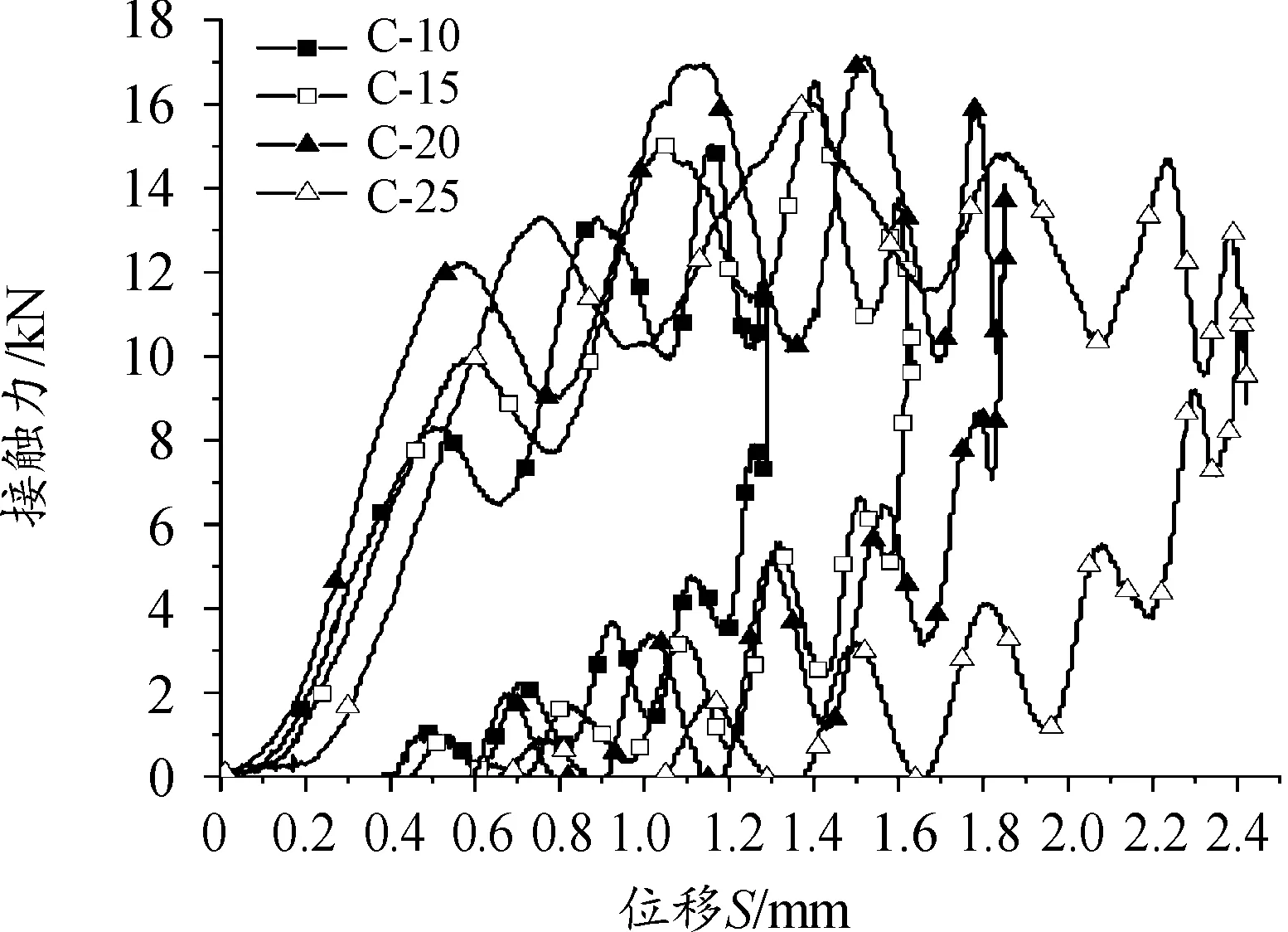
图5 四组试件的接触力-位移曲线

3.2 不同能量下位移-时间曲线

试件受到10 J、15 J、20 J、25 J四种能量冲击时的位移-时间曲线如图6所示。由图6可知四组试件的位移-时间曲线趋势基本一致，冲击头最大位移随冲击能量增大而增大，依次为1.29 mm、1.64 mm、1.85 mm、2.43 mm。能量较低时，纤维断裂等损伤情况较少，在试件表面上产生的凹坑较浅，随着冲击能量的增加，损伤继续扩展，凹坑直径和深度增加，冲击头的最大位移也相应增加。C-25组试验的冲击头最大位移大于碳纤复材试件厚度，观察发现试件背面存在凸起现象，表明在较高能量冲击下损伤已贯穿试件厚度，试件背面的45钢金属板上出现了圆形凹坑状塑性变形。

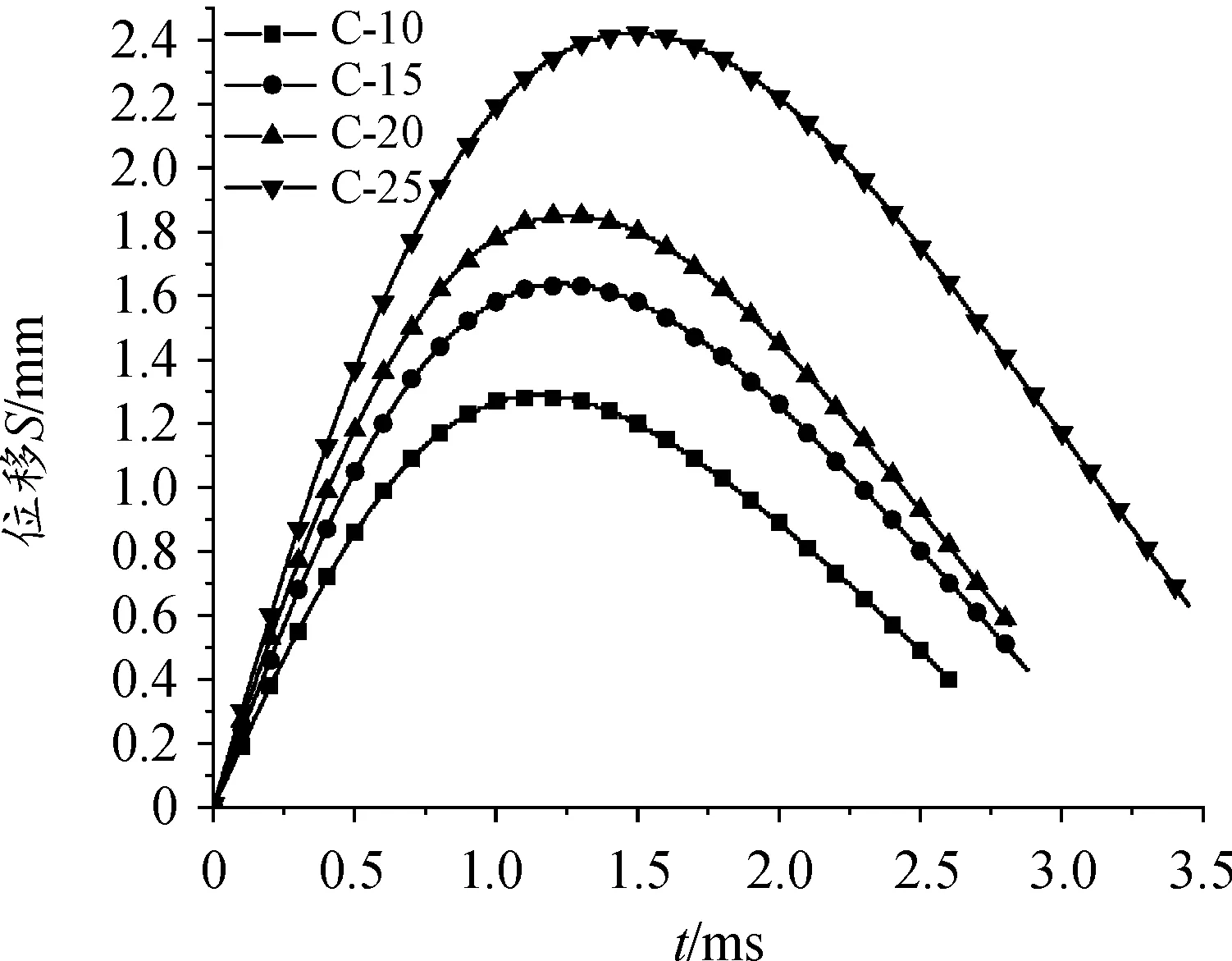
图6 位移-时间曲线

3.3 不同能量下冲头能量损耗-时间曲线

试件受到10 J、15 J、20 J、25 J四种能量冲击时的能量损耗-时间曲线如图7。能量损耗的定义如式(1)所示。由图7可知，4组试件的能量损耗趋势大致相同，呈现为“左陡右缓”特征。各试验组冲击头与试件脱离后损耗的能量依次是 7.83 J、11.94 J、16.03 J、21.84 J，损耗能量与初始冲击能量的比值分别为的78.30%、79.6%、80.3%、87.36%。初始冲击能量越高则损耗总能量和能量损耗率越高。冲击能量绝大部分被试件和刚性板吸收。试件受到冲击进入渐进损伤过程后，初始能量越高则能量的吸收速率越高，表明试件的损伤速率也越大，试件的损伤程度加剧，层合板吸能增加。

冲头动能损耗公式：

(1)

式中：v0为冲击头的初速度；v1为冲击头当前速度；m为冲击组件质量。

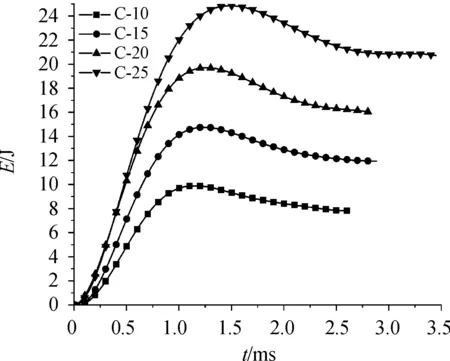
图7 能量损耗-时间曲线

4 有限元分析

4.1 有限元模型建立

建立碳纤维层合板冲击有限元模型。碳纤维层合板、冲击头、刚性板均采用八节点六面体线性减缩积分单元划分网格，每个铺层采用一层体单元。试件铺层之间均采用cohesive单元模拟层间胶层，使用八节点三维单元划分网格。细化层合板冲击区域网格，提高数值计算精度。为简化模型并减小计算量，试件两端四分之一的层合板表面与刚性板做节点融合，其他部分设置为接触对。冲击头和层合板试件设置为接触对，刚性板底面4个边的节点约束3个线自由度。由试验可知，冲击过程都在3.5 ms以内完成，因此将有限元分析的时间段设为5 ms,以冲击头与试件表面接触的时间点作为分析起始点。本文建立的是考虑材料非线性、接触非线性的高度非线性冲击问题分析模型。有限元模型及边界条件如图8所示。

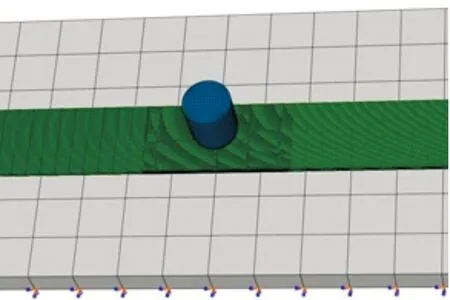
图8 有限元模型示意图

4.2 复合材料失效判据

国内外学者提出许多失效判据对材料不同形式损伤的产生和发展进行预测，最常使用的复合材料失效准则有Hashin[13]准则，Tsai-Wu[14]准则,Chang-Chang[15]准则,Hou[16]准则，最大应力准则等。本文采用基于应变的Chang-Chang准则[17-18]来判断纤维和基体的失效情况，失效判据如下：

1) 纤维拉伸失效(ε11≥0)

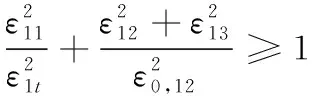
(2)

2) 纤维压缩失效(ε11<0)

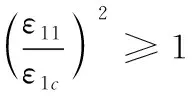
(3)

3) 基体拉伸失效(ε22≥0)

(4)

4) 基体压缩失效(ε22<0)

(5)

在以上各式中，

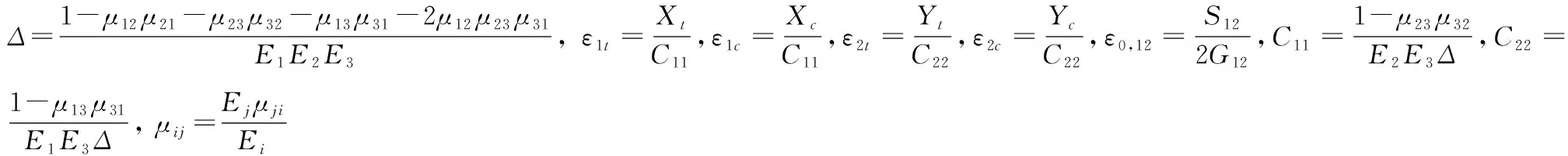
本文引入基于应变的损伤状态变量定义渐进损伤刚度折减方案。相较于直接进行参数折减，基于应变的损伤变量更加接近实际且损伤过程连续[19]，变量定义如下：

纤维拉伸：

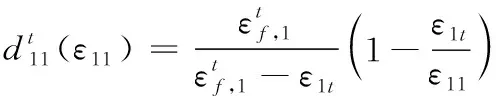
(6)

纤维压缩：

(7)

基体拉伸：

(8)

基体压缩：

(9)

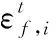
(10)

(11)

式中:σt为拉伸强度，σc为压缩强度,L为单元特征长度；Git为纤维或基体拉伸破坏的断裂韧性，Gic为纤维或基体压缩破坏的断裂韧性[17]。

(12)

本文使用cohesive单元模拟铺层间的分层损伤[20]。采用二次应力准则判断cohesive单元的初始损伤,公式如下：

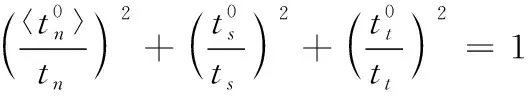
(13)

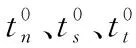
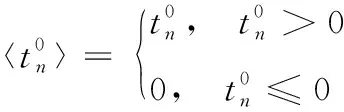
(14)

采用基于能量退化的BK准则[21]模拟胶层的性能退化。

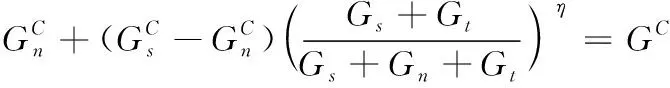
(15)

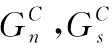
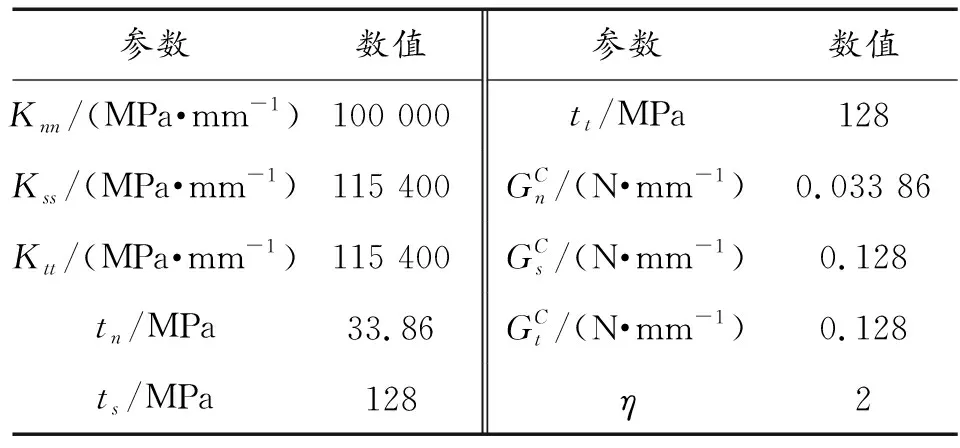
表3 COHESIVE单元材料参数

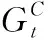
4.3 用户子程序计算流程

通过编写用户子程序实现材料损伤准则的自定义，计算流程如图9所示。

图9 子程序自定义损伤计算流程框图

4.4 计算结果分析

4.4.1基体与纤维损伤

通过显式动力学计算，对整个冲击过程进行分析。本文利用C-25组试验数据基于仿真与试验冲击时间-接触力合力曲线的重合度对有限元模型进行修正，表1所示材料参数为修正后的参数，另外3组试验的有限元模型均采用该物理参数。图10和图11给出了冲击过程结束后，C-10和C-20两个试验组冲击区域附近的基体拉伸损伤分布，第一层为冲击头直接接触的铺层。红色区域为基体拉伸损伤的单元，白色区域是失效后被删除的单元。由计算结果可知，试件受冲击后先出现基体损伤，再出现纤维损伤。损伤区域主要位于冲击点附近，且由冲击点沿纤维方向延展。原因是0°铺层的试件受冲击后纤维间的基体产生损伤，裂纹沿纤维方向扩展，符合基体拉伸损伤规律。各试验组基体拉伸损伤面积之和如图12所示，前3组试件的基体拉伸损伤面积随冲击能量增大呈线性增大趋势；冲击能量增加到25 J时，能量提高，损伤面积出现非线性趋势，曲线斜率变小。

图10 C-10组基体拉伸损伤云图

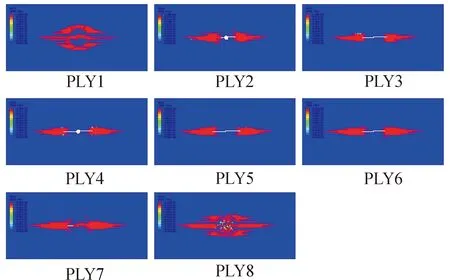
图11 C-20组基体拉伸损伤云图

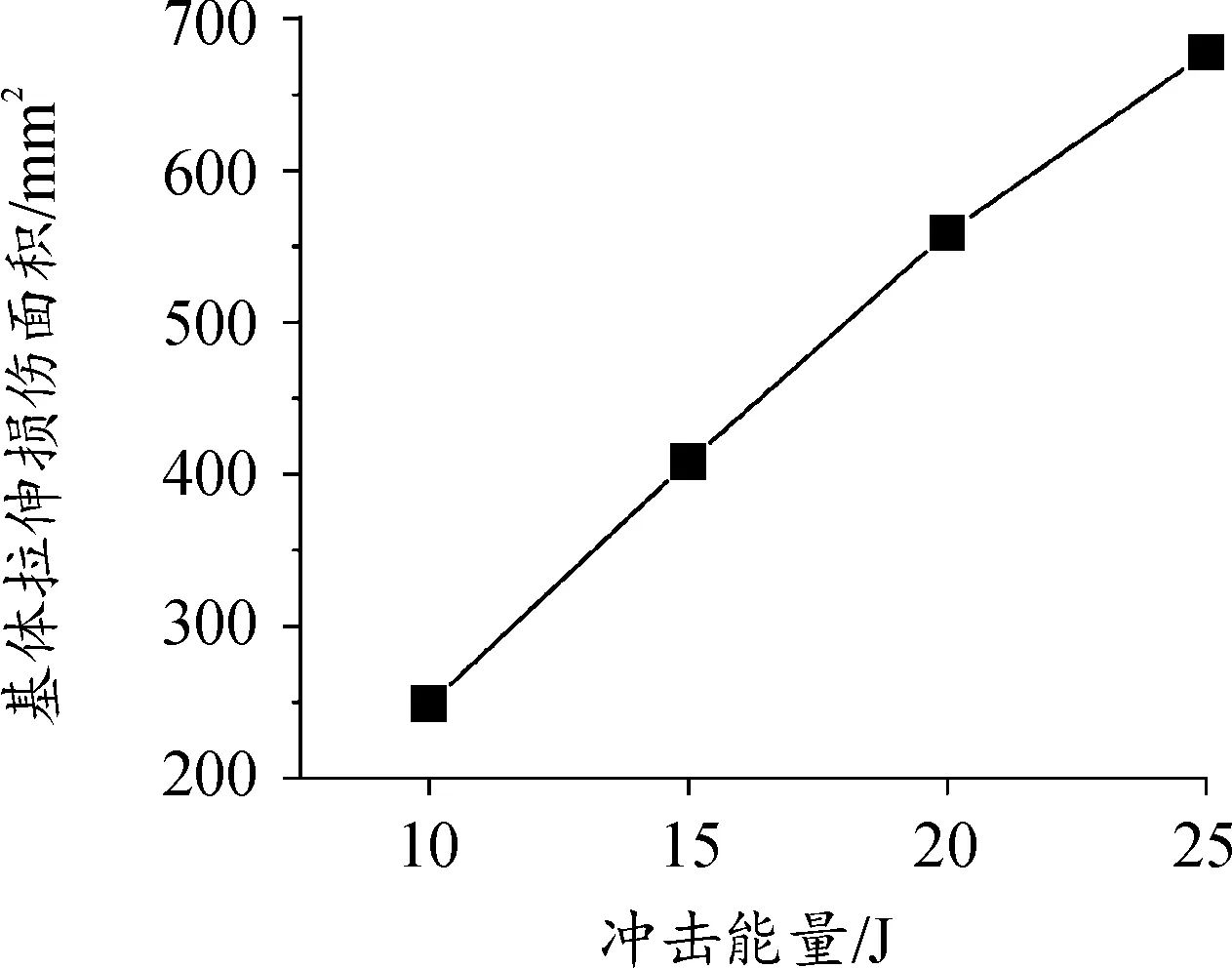
图12 基体拉伸损伤面积曲线

4.4.2层间损伤

定义cohesive单元刚度退化率SDEG(stiffness degradation)，公式如下：

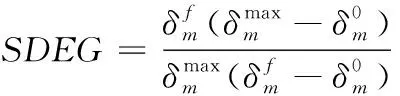
(16)

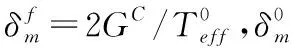
层合板的分层损伤在计算时体现为cohesive单元的失效，主要集中在冲击区域附近。由图13和图14可知，当冲击能量为10 J时，SDEG云图中冲击点附近出现较为规则的白色圆形区域，即为胶层失效后被删除的cohesive单元。其他颜色代表cohesive单元的不同SDEG数值。中心的红色区域由于被冲击头挤压，分层被抑制，因此cohesive单元未被删除。当冲击能量增大至20 J后，层间拉伸损伤加剧，冲击区域附近的cohesive单元刚度退化加剧，冲击区域的白色圆形区域开始沿纤维方向扩展。远离冲击点的区域，cohesive单元基本完好。由图可知，第七与第八铺层间的分层损伤面积最大。图15给出了不同冲击能量下，所有铺层的层间损伤面积之和；由图可知损伤面积基本随冲击能量的提高呈线性增大趋势，与基体拉伸损伤趋势一致。

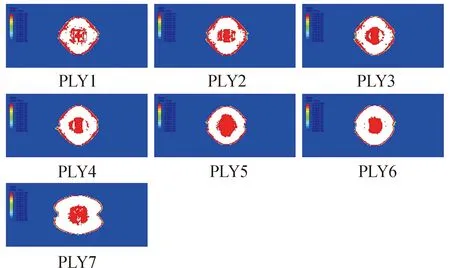
图13 C-10组cohesive单元刚度退化云图

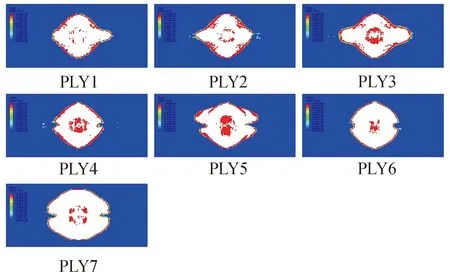
图14 C-20组cohesive单元刚度退化云图

图15 分层损伤面积曲线

4.4.3接触力对比分析

图16与图17所示为各试验组冲击头接触力合力CFNM(Magnitude of total force due to contact pressure)/时间曲线与数值计算结果。冲击试验机数据采集存在一定误差，且冲击过程中不可避免地会发生少量热耗散，高能量冲击时，钢材垫板出现了少量塑性变形，这些因素都会影响数值仿真结果与试验数据的吻合度，产生一定的误差。由图可知，仿真曲线相较于试验曲线有一定程度的升高，仿真曲线的峰值高于试验曲线，且达到峰值的时间晚于试验曲线，接触时间短于试验曲线。各试验组接触力合力峰值的误差分别为17.29%，18.3%，18.51%，17.08%。有望减小误差的方法包括：通过选用硬度更高的材料或对钢材表面进行热处理提高其表面硬度，抑制塑性变形导致能量的吸收；进一步精确测量冲击头的反弹速度，进而计算出更准确的冲击能量。考虑到复材冲击问题的复杂性，本文中的有限元分析模型能较为准确地模拟冲击过程。

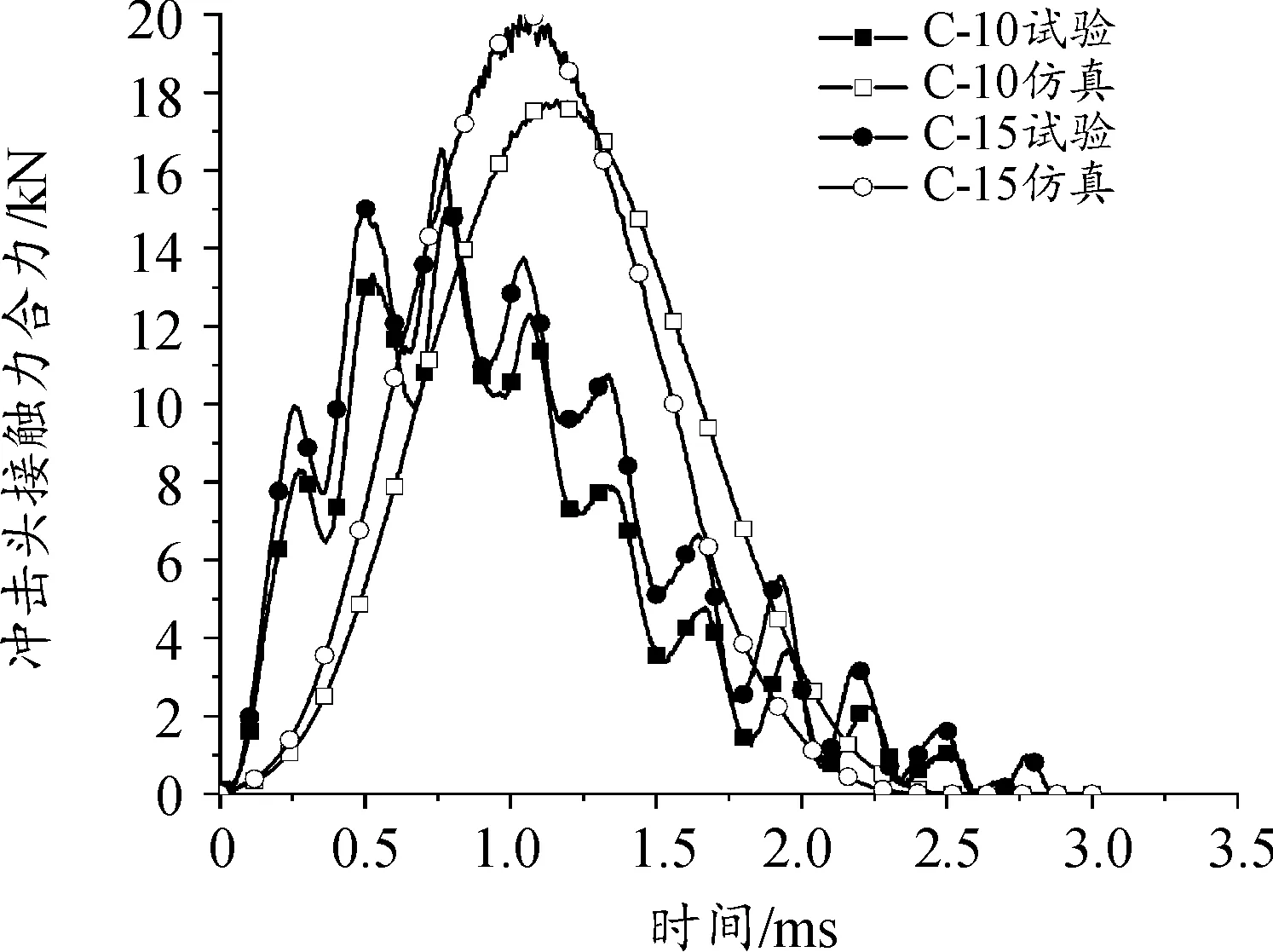
图16 C-10及C-15组接触压力合力-时间关系曲线

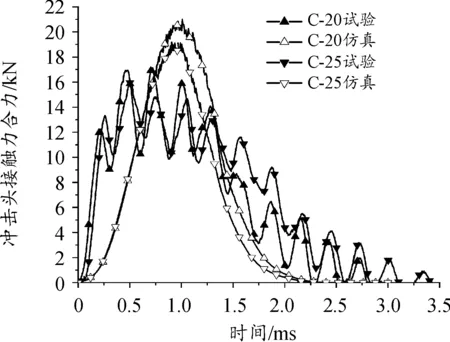
图17 C-20及C-25组接触压力合力-时间关系曲线

4.4.4试件形貌分析

图18为各试验组试件冲击后的表面形貌。由图可知，试件正面冲击点处产生了近圆形凹坑。C-10组试件背面无明显变化。C-15组试件冲击面凹坑相对C-10扩大，基体损伤更明显，试件背面出现轻微的分布基体短裂纹。C-20组试件凹坑直径继续增大，损伤程度加剧，试件背面出现长裂纹和轻微凸起。C-25组试件凹坑中的裂纹向周围扩展，损伤面积进一步增加，背面高高隆起，基体开裂、纤维断裂情况明显。

图18 冲击后表面形貌

图19为C-20组表面宏观形貌与数值计算得到的表面基体拉伸损伤分布图，计算结果与层合板宏观损伤状态基本吻合。

图19 C-20组宏观形貌

图20为使用PDV-IE200M电子显微镜拍摄的C-20组试件冲击区域局部细观形貌。由图20可知，冲击区中心和边缘均发生了基体压溃、开裂与纤维断裂，断裂区域有明显纤维拔出，体现为图18、图19的宏观裂纹。

图20 C-20组试件冲击区域细观形貌

5 结论

1) 受层合板渐进损伤进程影响，冲击头接触力合力峰值随冲击能量增大呈现先增大后减小；冲击头最大位移和能量损耗率随冲击能量增大呈单调上升。

2) 试件受冲击后先出现基体拉伸损伤，并由冲击区域沿纤维方向延展；低能量组试件的基体拉伸损伤面积随冲击能量增大呈线性增大，高能量组呈非线性增大；分层损伤主要集中在冲击区域，远离冲击点的区域胶层完好；分层面积随冲击能量增大呈线性增大；接触力合力峰值的最大计算误差为18.51%。

3) 冲击后正面出现明显的基体拉伸裂纹和纤维断裂，造成近圆形凹坑，损伤程度随能量增大而加剧；试件背面产生了分布基体短裂纹，随能量上升，裂纹沿纤维方向延展。冲击能量为25 J时，试件损伤贯穿整个厚度，试件背部隆起，底部刚性板产生塑性变形。

4) 数值计算损伤状态与试件实际损伤形貌基本吻合。

所建立的层合板非线性损伤有限元模型能够较为准确地分析冲击过程。