面向远场语音识别的回声消除算法及应用验证

司永凤，高云龙，王永娟

(南京理工大学 机械工程学院， 南京 210094)

1 引言

近些年恐怖袭击事件日益增多，面对暴虐的恐怖分子，需要谨慎安排救险工作才能将人质平安的解救出来。当内部劫持情况不明时，救险人员直接进入可能会对人质的生命安全造成威胁且自身也会有危险，这时就需要小型侦查类设备代替救险人员进入事故现场监听内部语音信息，方便采取行动。考虑到侦查工作的隐蔽性，设备只能远距离(通常1～10 m)采集声音信号，但由于真实环境中存在墙壁、障碍物等反射的干扰，导致拾取到的信号质量下降[1-2]，进而影响系统识别率。为解决这一问题，引入了回声消除技术。

现有的回声消除技术中，以自适应滤波[3]处理回声为主的方案较为常用，其中最小均方[4](least mean square,LMS)算法与归一化最小均方[5-6](NLMS)算法因其易于实现且复杂度低成为算法实现中采用最多的算法。NLMS算法是在LMS算法的基础上，通过将固定步长改为可变步长，解决了输入信号相关情况下LMS算法收敛速度慢的问题,但它受噪声影响较大,稳态性能有待提高。为了解决这一问题，人们相继提出了很多改进的变步长LMS算法，意图通过变步长平衡收敛速度与稳态误差之间的关系。覃景繁等[7]提出了一种新变步长LMS算法(sigmoid variable step least mean square,SVSLMS)，其原理是利用步长与误差之间的非线性函数关系实现收敛速度与稳态误差之间的平衡，但算法收敛完成后，步长受误差影响较大，这种平衡不再维持。为了提升算法性能，程建民等[8]基于双曲正弦函数提出了变步长LMS改进算法，通过将瞬时误差与步长值相关联，在满足步长调整原则的基础上，实现了对步长值的动态调整。之后，刘宪爽等[9]基于Sigmoid函数对算法提出了改进，使其稳定性与准确度得到了有效提升。

实际应用中，如何在收敛速度、稳态误差、计算量等各方面做到兼顾是自适应滤波算法设计中的关键。基于上述分析，本文中将NLMS算法与步长调整原则相结合，通过对语音识别原理及远场回声的分析，提出了一种基于双曲正弦函数的变步长NLMS改进算法，搭建相应的远场语音识别试验平台，结合嵌入式设备树莓派Zero WH对该算法测试，以验证改进算法降低系统词错误率的有效性。

2 远场回声产生原理

声学回声的产生与周围复杂多变的环境有关，在远端环境中，根据室内物品的摆放，远端扬声器播放的近端语音信号可能被环境内多个物体反射后形成回声信号被麦克风采集或不经过物体反射直接被麦克风采集。回声产生原理如图1所示，空旷房间内，远端说话人声音通过多种路径反射形成了回声语音信号，因此麦克风除远端说话人声外还采集到了回声信号，影响了输入端语音信号的质量[10]。

图1 回声产生原理示意图

3 变步长NLMS改进算法

3.1 NLMS算法

到目前为止，多种自适应滤波算法被提出并得到推广应用。原理主要是：自适应滤波器模拟和追踪真实的 “回声路径”，并由收敛出的“回声路径”(滤波器系数)对回声做出估计，再从近端纯净语音与回声叠加后的信号中减去估计的回声，从而到达消除回声目的[11]。

图2为回声消除技术基本原理示意图。其中，回声y′(n)是远端输入信号x(n)与回声路径W′(n)线性卷积的结果，y(n)是对回声y′(n)的估计，W(n)是对真实回声路径W′(n) 的模拟，e(n)为自适应滤波器输出的残差信号，表示估计的回声与真实回声之间的误差值，可用式(1)表示：

e(n)=d(n)-y(n)

(1)

其中：

d(n)=y′(n)+ν(n)=W′T(n)x(n)+ν(n)

y(n)=WT(n)x(n)

为防止回声路径发生缓变或突变时抑制回声能量的问题，滤波器必须及时调整自身系数以“跟踪”回声路径的变化，因此必须用自适应算法实时更新滤波器W(n)，NLMS算法迭代公式为[12-13]

(2)

式(1)中：μ/xT(n)x(n)+δ为可变的步长因子，与远端输入信号x(n)的自相关矩阵xT(n)x(n)有关，能够加快收敛速度。δ为一取值较小的正常数，以防止当输入信号过小时而带来的算法性能的不稳定性。

图2 回声消除技术基本原理图

NLMS算法相比于经典的LMS算法优势在于不增加计算复杂度的前提下，具有更快的收敛速度，但其本身也存在一些性能上的缺陷，即收敛速度虽快，但随着迭代的进行，收敛速度一直在下降，影响回声消除的效果。因此，文中对NLMS算法提出改进，尝试分析步长因子随迭代次数变化的有关规律。

3.2 NLMS改进算法

变步长NLMS改进算法的设计思想是使步长和误差之间满足一种函数关系，以误差为可调节的自变量来控制步长，使其始终在满足使用要求的某一范围值内。双曲正弦函数[14]是双曲函数的一种，该函数关于原点对称，具有严格单调性，通过引入幅度因子a、b和指数c对其作简单线性变换，可以得到步长调整函数表达式为

μ(n)=a*|sinh[b*e(n)c]|

(3)

其中，参数a用于控制取值范围，参数b、c用于控制图形形状。

图3所示为步长调整函数曲线，可以看出，NLMS改进算法在初始收敛过程中误差值e(n)较大，此时函数也提供了较大的步长值μ(n)，使得改进算法具有较快的收敛速度；而在算法收敛完成后，自适应滤波器W(n) 已接近回声路径W′(n)，误差值e(n)接近于零，此时回声信号得到了有效抑制，函数对应的步长值μ(n)维持在一个较小的范围值内，有利于算法在该过程中保持更好的稳定性，证实了该函数满足步长调整原则。

图3 步长调整函数曲线

本文改进算法的迭代步骤:

算法：NLMS改进算法

参数：μ：步长因子L：自适应滤波器的长度

初始条件：ω(0)=0

输入：x(n)=[x(n),x(n-1),…,x(n-L+1)]T

ω(n)=[ω1(n),ω2(n),…,ωL(n)]T

滤波：y(n)=WT(n)x(n)

误差估计：e(n)=d(n)-y(n)

步长函数：μ(n)=a*|sinh[b*e(n)c]|

为了直观分析步长调整函数中参数a、b、c对算法收敛速度的影响，在满足步长稳定条件下，通过试错法[15-16]分别对各参数的取值原则和范围进行讨论以获得最优取值。其中，图4(a)条件设为b、c值保持不变，a分别取0.01、0.02、0.05；图4(b)条件设为a、c值保持不变，b分别取1、1.5、2；图4(c)设为a、b值保持不变，c分别取值1、2、4。

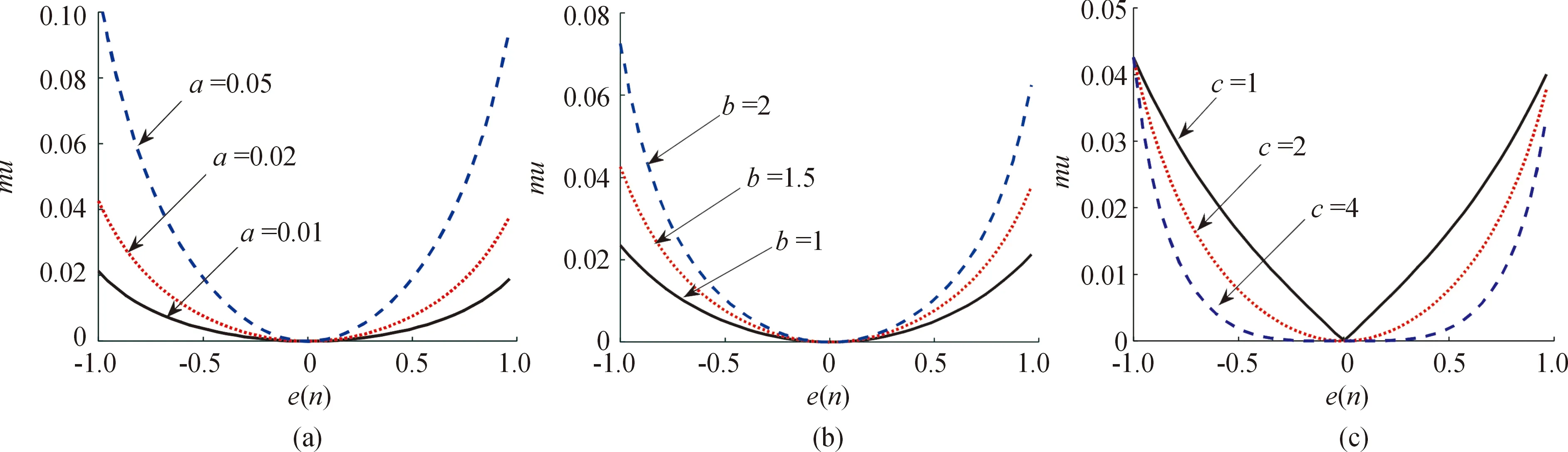
图4 误差e(n)与步长μ(n)之间的关系曲线

分析图4(a)、图(b)所对应的步长调整曲线可知，参数a、b主要作用是调节函数曲线的幅值。a、b取值越小步长因子在误差接近零处变化越小，但在算法收敛初期不能够为算法提供较大的步长取值，算法收敛速度较慢；当a、b取值较大时，能够提供较大的步长取值使算法有较快的收敛速度，但同时步长因子在误差接近零点处变化较快，可能错过最佳步长值影响算法的稳定性。因此，在本仿真环境下，为获得更快的收敛速度和更优的稳定性，参数a、b分别取值为0.02、1.5时，算法性能相对更优。

分析图4(c)所对应的步长调整曲线可知，参数c主要作用是调节函数误差接近零点处的曲线平滑程度。c取值越大，函数误差接近零点处的曲线越平滑，算法在收敛完成阶段越稳定，但考虑到c对应指数函数，增大后将大大增加计算量，因此参数c取适中值2时，算法性能相对更优。

3.3 算法对比

基于Matlab平台对算法模拟仿真，分析NLMS算法[13]、文献[8]算法、SVSLMS算法[7]与文中基于双曲正弦函数提出的变步长NLMS改进算法之间的差异性。考虑到实际远场识别环境中混响以及回声影响比较强，仿真条件设置为信干比SIR分别为5 dB和10 dB时，自适应滤波器阶数为8，音频采样点数为1 000的独立仿真试验。最终得到以均方误差(mean square error,MSE)为评价标准的算法收敛对比曲线，分别如图5(a)、图5(b)所示。

图5(a)可以看出：在信干比为5 dB的情况下,NLMS算法的稳态误差较大，文献[8]算法以及SVSLMS算法的收敛速度相比于本文中NLMS改进算法较慢；增加干扰信号的强度后，改进算法的优势更加明显，由图5(b)可知，文中基于双曲正弦函数的变步长NLMS改进算法收敛速度最快，并且在收敛完成后，算法仍能稳定地保持在一个较小的均方误差下。在仿真验证理论分析正确的同时，也表明文中提出的变步长NLMS改进算法性能更优。

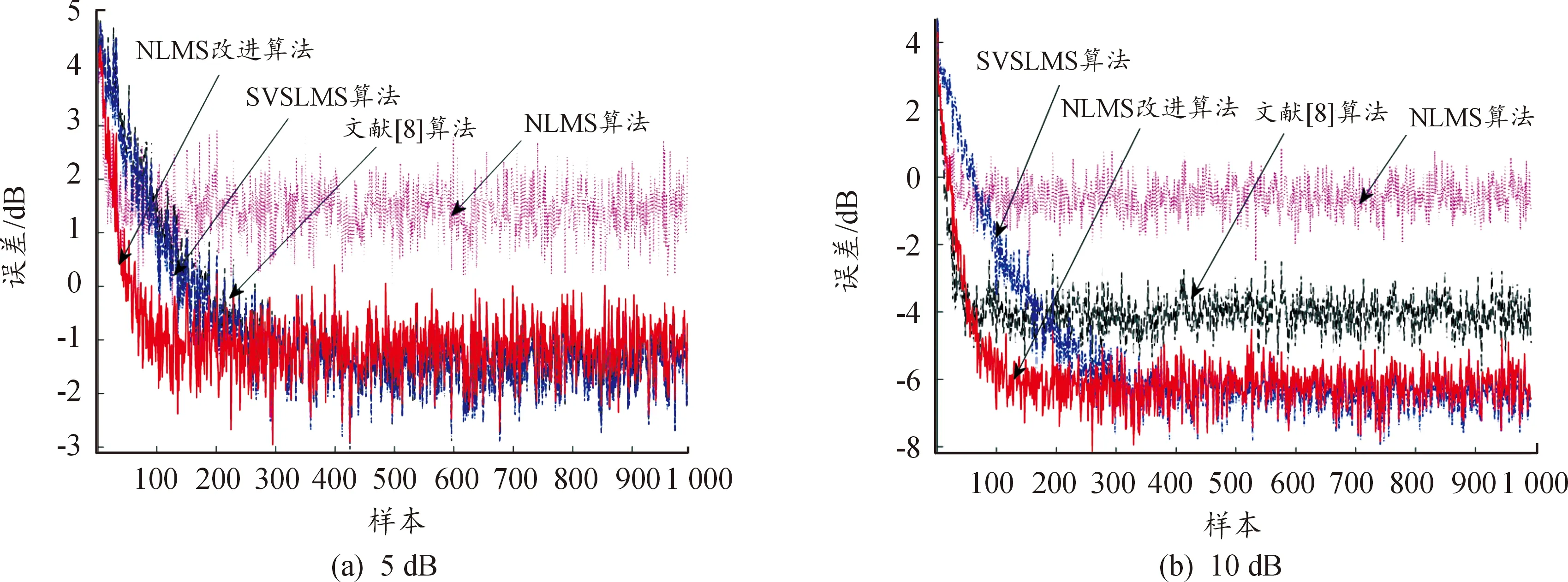
图5 算法收敛曲线

4 基于远场语音识别系统的算法验证

回声消除技术是语音识别系统中的关键步骤，有效的回声抑制可以提高音频信号的整体识别效果。为测试改进算法实际应用时的有效性，现基于Python语言搭建了远场语音识别系统，并将其移植到嵌入式硬件平台上做进一步验证。

4.1 算法验证平台搭建

本文中基于Linux操作系统完成了语音识别嵌入式软件程序设计，主要包括信号采集程序和语音识别主程序两部分。

准确地捕捉到声音信号是语音识别系统流程中关键的一步，程序设计思路是设定一个声音阈值，通过不断将采集到的信号与阈值进行比较，实现语音信号的采集。语音识别主程序主要包括特征提取与模型解码，首先利用标准数据库语音对搭建好的模型进行训练，从而得出该模型的参数，当未知语音输入时，提取待识别语音的梅尔频率倒谱系数(mel frequency cepstrum coefficient，MFCC)特征值，通过模型解码即可得到识别结果。具体算法流程如图6所示。

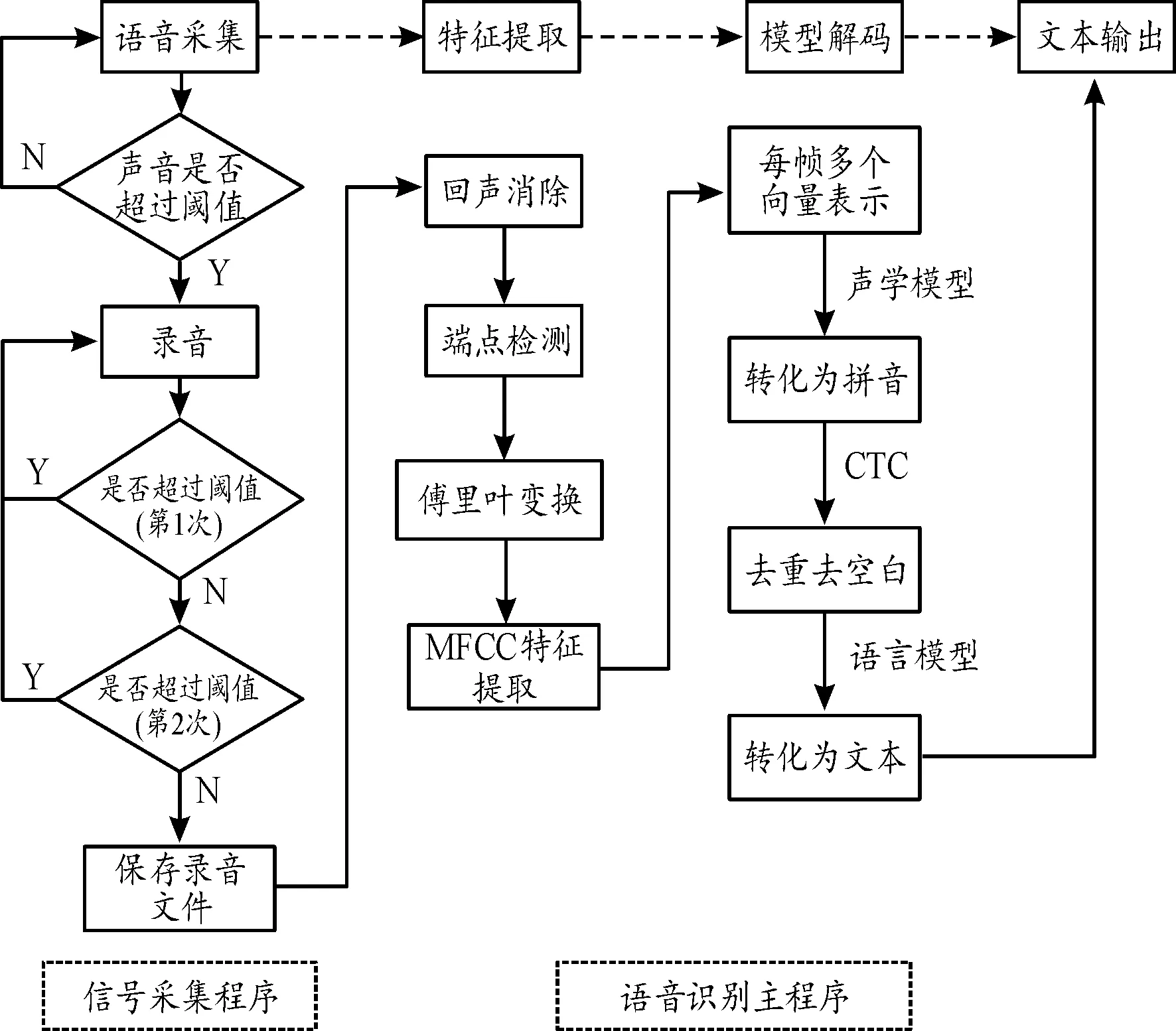
图6 软件流程框图

语音识别系统硬件平台结构体系如图7所示，采用树莓派Zero WH作为系统移动端，搭配ReSpeaker 2-Mics Pi HAT双麦克风阵列板采集语音信号。工作时，树莓派Zero WH与宿主机通过网络连接，在宿主机上远程登录树莓派操作系统作为虚拟终端执行语音采集命令，再将采集到的语音信号传到上位机(宿主机)端进行语音识别操作，最终输出识别结果。

图7 硬件平台结构体系框图

4.2 算法性能测试与分析

1) 测试数据。测试所用数据集包括标准数据集以及本人录制的音频样本。其中，标准数据集为开源的THCHS30、ST-CMDS中文数据库，另一部分音频样本是在信噪比 40 dB的安静环境下采用双麦克风阵列板录制的采样频率为16 kHz、采样大小为16 bits的纯净音频文件。此外为了增强语音识别模型的适应性及抗干扰性，将纯净音频与回声模型2[17]做卷积运算得到含噪语音，将其引入数据库中实现数据集的扩充。采用词错误率(word error rate,WER)对系统识别率做评估，其计算公式为

(4)

式中:T是识别结果总词数，S、D、I分别是替代错误、删除错误、插入错误的词数，WER值越小说明系统识别效果越好。

2) 模型构建。语音识别网络结构体系如图8所示，语音文件转化为频谱图作为模型输入，首先经过5次卷积-Dropout-卷积-最大池化-Dropout的循环，其中Dropout层目的是降低方差，防止模型过拟合；在最后一次循环的Dropout层之前加入一个Reshape层改变输入数据的维数，实现对不同层的连接；之后再连接2个带有Dropout层的全连接层网络，对提取到的特征进行整合分类，最后通过Softmax层连接CTC(connectionist temporal classification)模型，使用CTC的loss作为损失函数，实现连接性时序多输出。

图8 CNN-CTC网络结构体系框图

CTC[18-21]作为一种端到端的语音识别方式，不需要在帧级别上对其标签，它可以根据输入的每帧预测信息，寻找具有最高概率的标签序列进行输出，大大简化了声学模型的训练过程。网络模型参数设置如表2所示。

表2 网络模型参数

3) 试验结果与分析。语音信号是一种短时平稳信号，不同帧内语音的信噪比不同，为了更好地表征语音信号的性能，采用频率加权分段信噪比(frequency-weightedsegmented speech signal-to-noise ratio,FWSSSNR)作为语音质量评价指标，且FWSSSNR数值越高，表示该段语音信号质量越好。

从验证集和录制的纯净音频样本中随机选取10句音频文件，分别与回声模型2做卷积运算得到最终语音信号。通过改进算法对合成后的语音信号做回声消除，进一步地，采用FWSSSNR指标分别对NLMS算法(算法Ⅰ)和NLMS改进算法(算法Ⅱ)处理后的语音信号质量进行评价。

由图9可知，采用算法Ⅱ对混合语音信号做回声消除后，回声部分波形几乎被完全消除，且图10所示不同算法对应的FWSSSNR结果进一步证明，加入回声后的语音经2种算法处理后，FWSSSNR数值均有所提升，但算法Ⅱ相比算法Ⅰ性能更优、增强效果更明显。

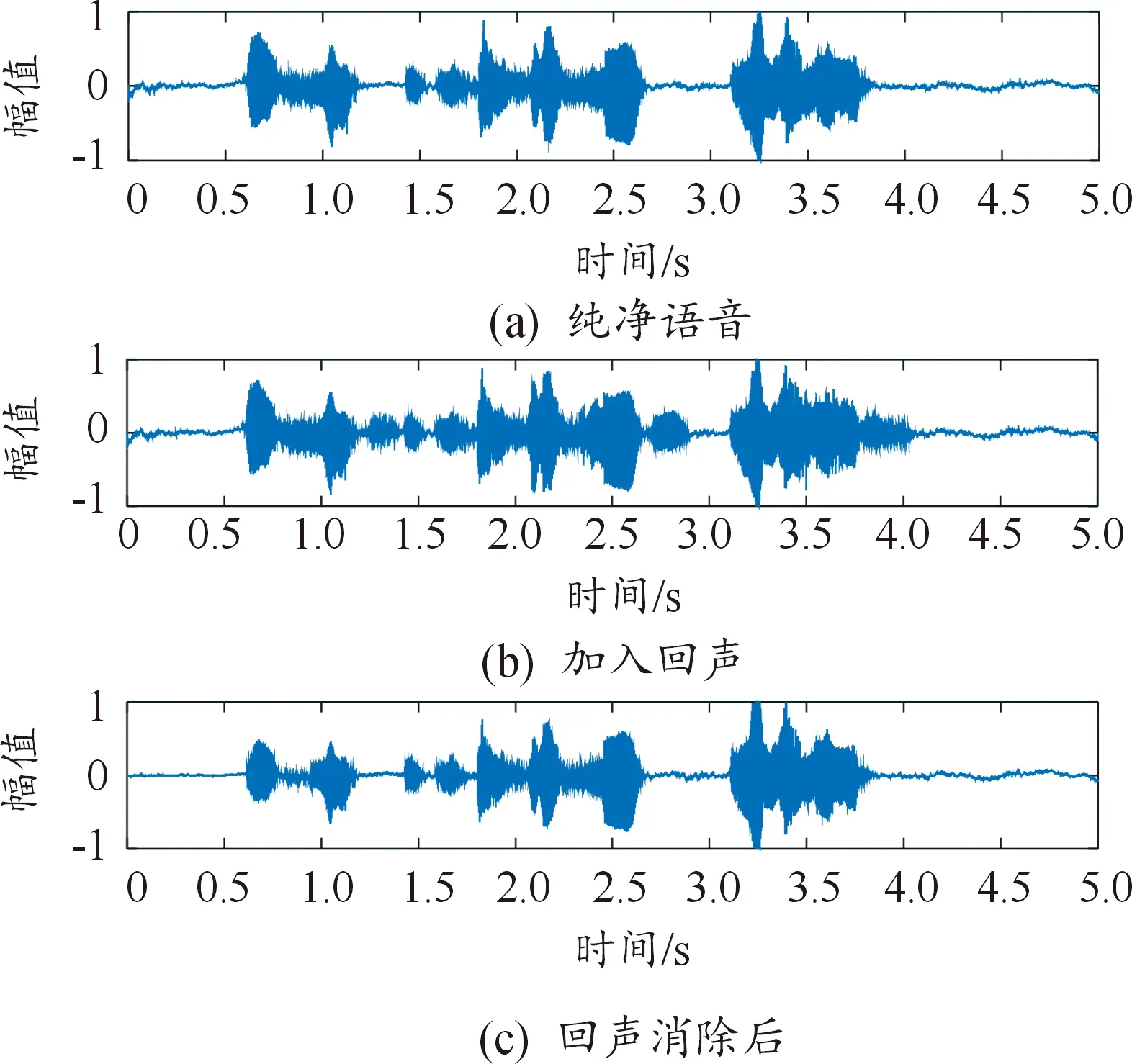
图9 基于算法Ⅱ的语音波形曲线Fig.9 Speech waveform based on algorithm Ⅱ

图10 不同算法FWSSSNR直方图

表3所示为系统识别率测试结果，其中Δ为算法Ⅱ与算法Ⅰ之间的错误率差值。可以看出，加入回声后的语音词错误率高达60%以上，通过2种算法做语音增强后，系统词错误率明显降低，且采用算法Ⅱ比采用算法Ⅰ的词错误率降低了约10%，系统平均识别率在80%左右，验证了基于双曲正弦函数的NLMS改进算法在实际应用中的有效性。

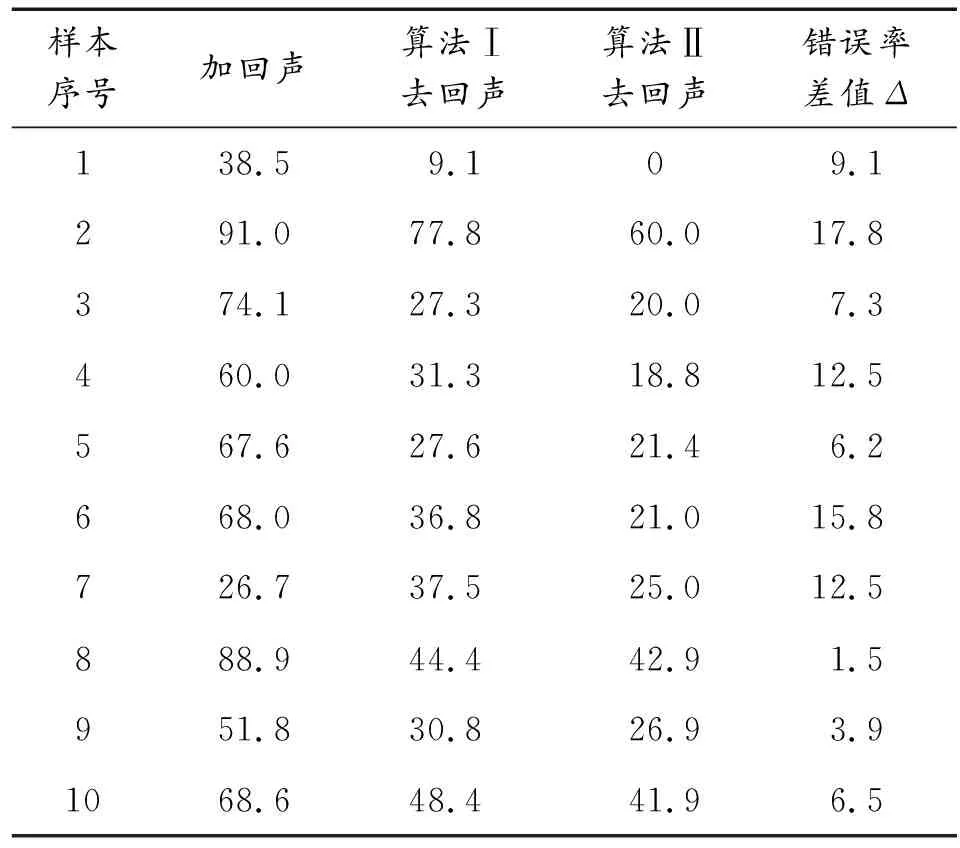
表3 语音识别系统回声消除前后的词错误率

5 结论

在现有语音识别技术的基础上，针对复杂背景中回声影响系统识别率的问题，提出了基于双曲正弦函数的变步长NLMS改进算法，经仿真验证，改进算法具有实时调整步长、不增大收敛误差的条件下具有更快收敛速度的优势。

通过搭建嵌入式硬件平台对算法实际性能进行测试，结果表明，应用改进算法做回声消除后系统词错误率降低了约10%，平均识别率得到了明显提升，在远场语音识别中具有实际应用价值。