可见光系统信道估计导频优化算法研究*

胡晓莉，李永伟，秦岭，王凤英

（内蒙古科技大学 信息工程学院，内蒙古 包头 014010）

在室内非视距链路（Non Line of Sight，NLOS）传输下，光源由于满足朗伯辐射模型，接收器在边缘位置接收到的信号呈现稀疏性，导致通信系统误码率较高.

信道估计就是得到传输信道的冲激响应，使得接收端准确地解调出发射信号，提高通信的性能[1，2].传统的信道估计算法如：最小二乘算法和最小均方误差算法，它们的实现都需要大量的导频[3]，而在ACO-OFDM系统中子载波的实际利用率为原本的，这就使有限的有效子载波资源更加紧张.现有研究成果表明将压缩感知（Compressed Sensing，CS）技术应用到ACO-OFDM系统信道估计中，不仅可以减少导频的使用个数，而且为室内可见光通信系统提供准确高速的链路性能.

基于压缩感知的稀疏信号重构算法的实现需要已知观测矩阵和恢复矩阵，研究表明恢复矩阵的互相关性越小，信号的恢复质量越高.文章通过对室内NLOS通信环境进行建模，对文献[4]提出的树状导频随机搜索算法进行分支裁，提出改进型树状导频随机搜索（Modified-Tree-based Stochastic Search Algorithm，M-TSS）算法，并将该算法运用到通信系统中.

1 压缩感知与信道建模

1.1 压缩感知稀疏信号表示

信号x为N×1的原始信号，若信号x可由一组N×N正交基Ψ＝[Ψ1，Ψ2，…，Ψn]线性表示，则信号可以如下式表示：

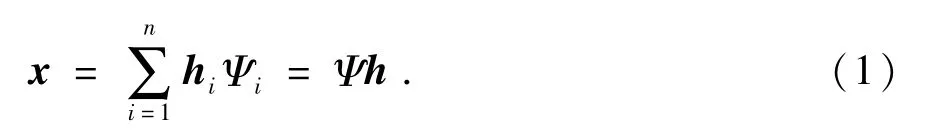
式中：h为N×1维加权系数向量.再用一个M×N维的观测矩阵Ф去观测信号值x，得到M×1维观测信号y，由上式可得：

在压缩感知的信号重构问题中，把式（2）可以写成：

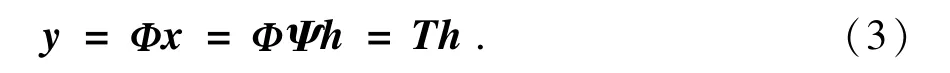
式中：观测矩阵Ф和基矩阵Ψ的乘积为恢复矩阵T.

1.2 NLOS下稀疏信道模型

如图1所示，将LED看作1个点发射源S，将接收器看作为R，AR和FOV为接收器的接受面积和接收视场角.

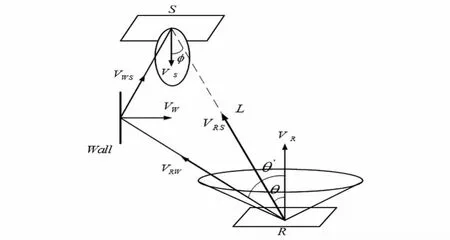
图1 室内可见光通信链路示意

LOS下室内VLC系统脉冲响应可表示为[5]：

式中：m表示朗伯辐射阶数，φ为发射光线与光源法线的夹角，°；θ为接收器的入射光线和接收器的位置法线的夹角，°；rect为矩形函数；ζ（x）为狄拉克函数；c为真空中的光速，m／s.

对于NLOS，LED发射单元经过k次反射到达接收器的脉冲响应为[5]：

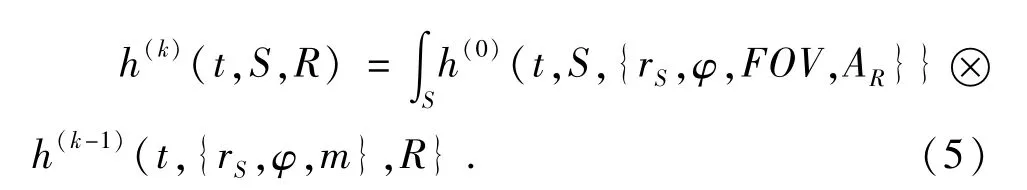
式中：∫s表示对所有反射元的积分，h（0）（t）为LOS下的脉冲响应，h（k-1）（t）是经过k-1次反射后的脉冲响应.特别当k＝1时，系统的脉冲响应为[6]：

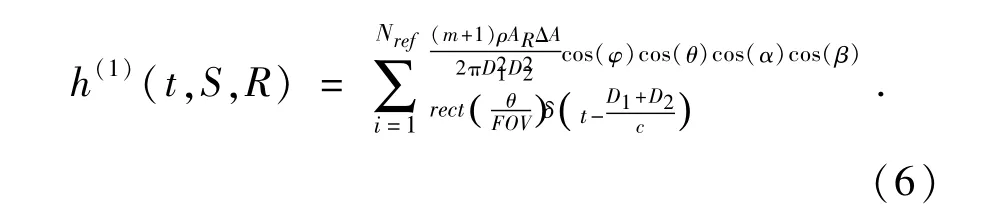
式中：Nref为反射面元的个数；ΔA为反射面元的面积，m2；ρ为反射体的反射率；α为光源与反射面元位置法线的夹角，°；β为反射面元法线与接收器的夹角，°.

表1为信道建模参数设置，图2为仿真得到的时域脉冲响应图.

表1 参数设置

从图2可以看出，室内可见光在NLOS链路下为标准的时域稀疏信道.发送端发送光信号，经过多径信道后，接收端检测光信号并且转化为电信号，可表示为：

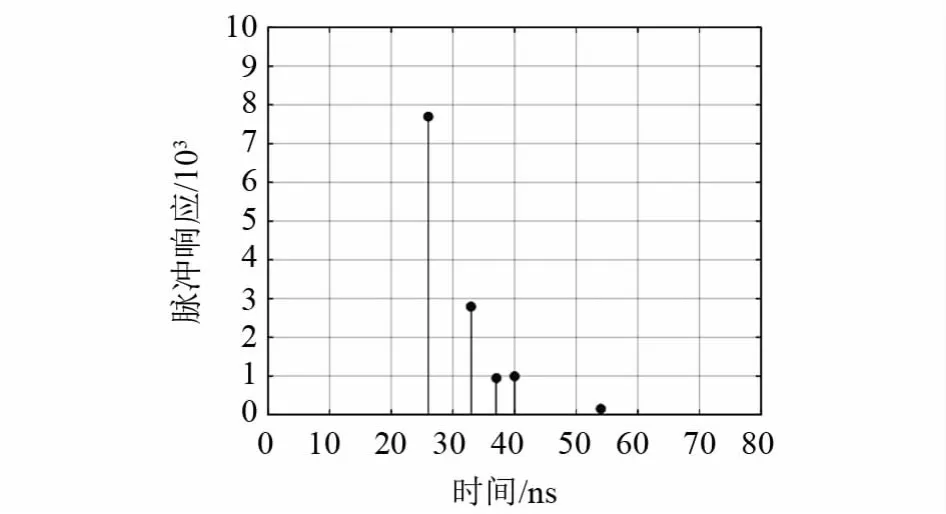
图2 时域脉冲响应

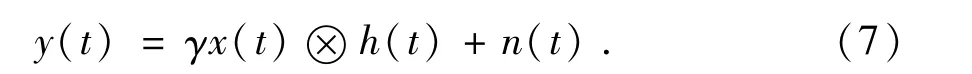
式中：γ为接收器的光电转换率，h（t）为时域脉冲响应，x（t）为发送端发送的数据，⊗为卷积符号，n（t）为高斯白噪声.

1.3 基于压缩感知的ACO-OFDM信道估计模型

由于ACO-OFDM系统仅使用奇数子载波传递信息.假设ACO-OFDM系统使用了P个导频（P为偶数），那么导频间有如下关系[7]：

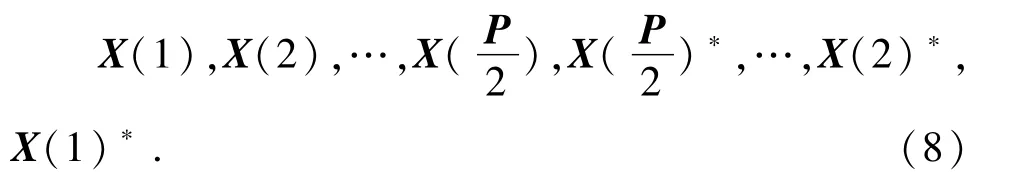
式中：（·）*表示共轭.

假设发射端采用的导频索引集n＝[n1，n2，…，np]，则发送和接收的导频符号数为：X（n1），X（n2），…，X（np）和Y（n1），Y（n2），…，Y（np），W为P×L维快速傅里叶变换矩阵，H为信道时域脉冲响应，V为高斯白噪声.

ACO-OFDM系统接收导频信号为：

式中：由向量形式表示记作：

这样将ACO-OFDM信道估计问题转变为压缩感知的信号重构问题，由于脉冲响应系数H具有稀疏性，因此对NLOS信道估计问题转化为压缩感知领域的信号稀疏重构问题[8].

2 改进型树状导频随机搜索算法

CS的最新研究进展表明，当恢复矩阵T满足约束等距特性（Restricted Isometry Property，RIP）时，就可以使用观测矩阵和恢复矩阵来重建稀疏矩阵，然而由于RIP准则在实际运用中复杂度较高，因此，通常采用复杂度较低的互不相关特性准则（Mutual Incoherence Property，MIP）当作恢复矩阵优劣的衡量标准.将MIP视为恢复矩阵T的设计准则，进行导频优化.将矩阵的相关性定义为2个不同列之间的最大绝对相关性，表示为：

当我们假设导频符号取值相同时：

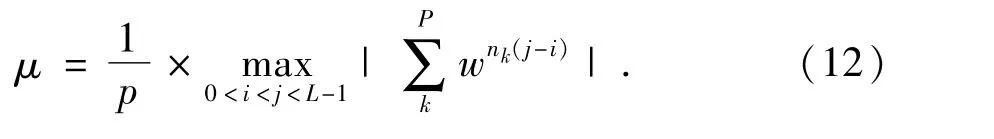
式中：w＝e-j2π／N.

传统的导频优化算法比如：导频索引位置穷举法和随机导频搜索策略，穷举法顾名思义就是把所有的导频图案列举出来并计算各自的μ值，选择μ值最小的为最终的导频图案；随机搜索策略就是尽可能列举多的导频图案求对应的μ值，只要列举的导频图案足够多，那么求得的μ值就越准确.这2种算法不仅仅运算复杂度高，而且算法在进行过程中容易陷入局部最优化问题，为了有效地解决上述问题，文献[4]提出TSS算法.该算法采用树状搜索结构，一次迭代中多个子集共同参与，不仅避免了局部最优化问题，而且运算复杂度也大大降低，但是TSS算法在运算复杂度上并不是最优的，文章在TSS算法基础上加入树的裁剪策略，对父节点的μ值采用阈值限制策略，对子生成树个数进行控制，使得算法在运算精度不减的情况下，运算时间进一步缩减.

算法具体步骤由表2可知.

表2 算法步骤

假设集合C＝｛1，2，3，4，5｝，导频个数为3，M＝2，则随机抽取3个子载波作为导频，即P＝｛1，3，5｝，当m等于1时Fl，m＝｛3，5｝，Cl，m＝｛1，2，4｝，用Cl，m中的元素一次替换集合P中｛1｝的位置，则生成｛1，3，5｝，｛2，3，5｝，｛4，3，5｝3个导频图案，再从这3个导频图案中选出μ值最小的2个为下一次迭代的父节点，以此类推，直到迭代结束输出最小的μ值和对应导频图案，TSS算法流程如图3所示.

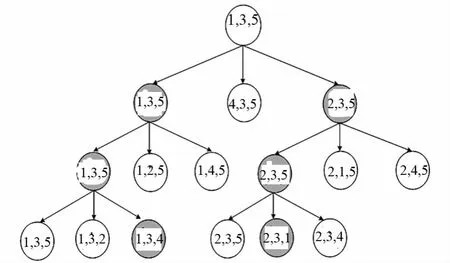
图3 TSS算法流程示意图

M-TSS算法流程如图4所示，算法在进行第三次迭代时，TSS算法的子存活树数目依旧为2，而此时M-TSS算法减少了子存活树的个数变为1，原因是在第二次迭代结束后，μ值满足阈值条件故减少子生成树的个数.然而在实际情况下，子载波的数目要远大于5，导频数也远多于3个，所以尽量要保证子存活数要大于1，这样才能避免局部最优化问题的发生.

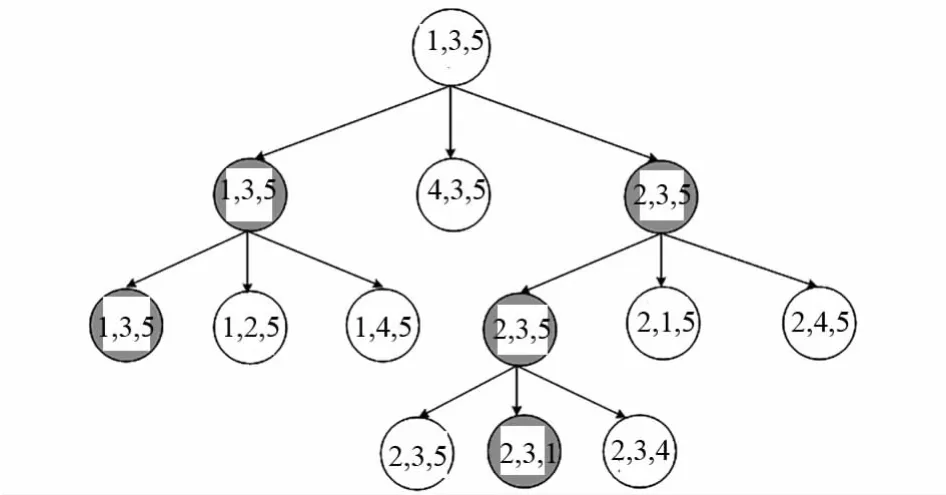
图4 M-TSS算法流程示意图

3 仿真结果分析

文章主要比较了TSS算法和M-TSS算法在室内可见光NLOS链路下的估计性能.

仿真参数如下：子载波为1024，采用16QAM技术，导频以梳状方式插入，比特出错概率（BER）和均方误差（Mean Square Error，MSE）作为估计精度衡量指标；为了兼顾运算速度和精度，子节点存活个数M设置为6，导频个数分别为64和128，仿真次数各为1000次，采用OMP算法进行信道估计.

图5为导频为64时BER仿真图，仿真图显示，在没有经过任何编码时，以等间隔导频插入的方式进行信道估计时系统BER是极高的，相较于等间隔导频插入和随机导频插入，采用TSS和改进算法导频插入方式时系统的BER明显降低，图6为MSE仿真图可见改进算法和TSS重构精度相比于等间隔和随机导频插入的要高很多，此时改进算法和TSS生成导频图案μ值分别为0.2620和0.2641；表3为改进算法和TSS算法运行一次的运算时间，改进算法由于增加了裁剪策略运算复杂度大大降低，大约为TSS算法的1／4.

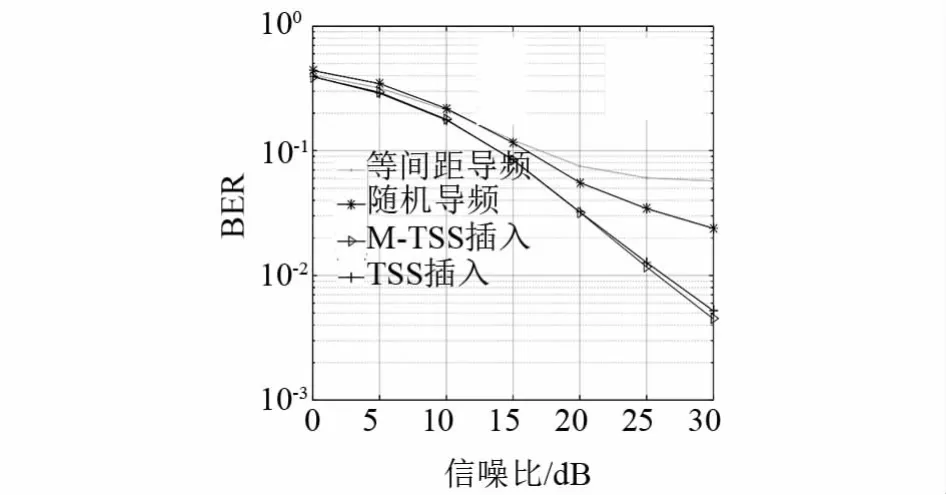
图5 导频为64时BER仿真图

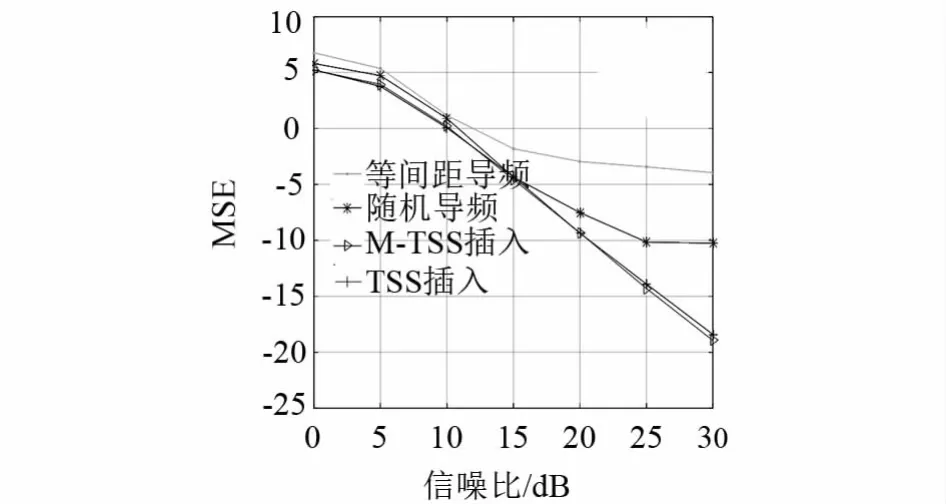
图6 导频为64时MSE仿真图

表3 导频为64时1次运行时间和子路径数比较

图7为导频为128时BER仿真图，仿真图显示：随着导频数目的增加，信道估计越准确，系统通信BER越低，相较于等间隔导频插入采用TSS和改进算法导频插入方式时系统的BER明显降低，优势明显，图8为对应的MSE仿真图，此时改进算法和TSS生成导频图案μ值分别为0.1580和0.1611；表4为改进算法和TSS算法运行一次的运算时间，在运算复杂度上改进算法具有明显的优势.

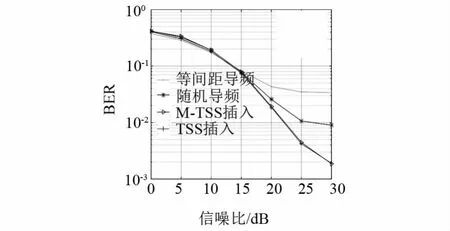
图7 导频为128时BER仿真图

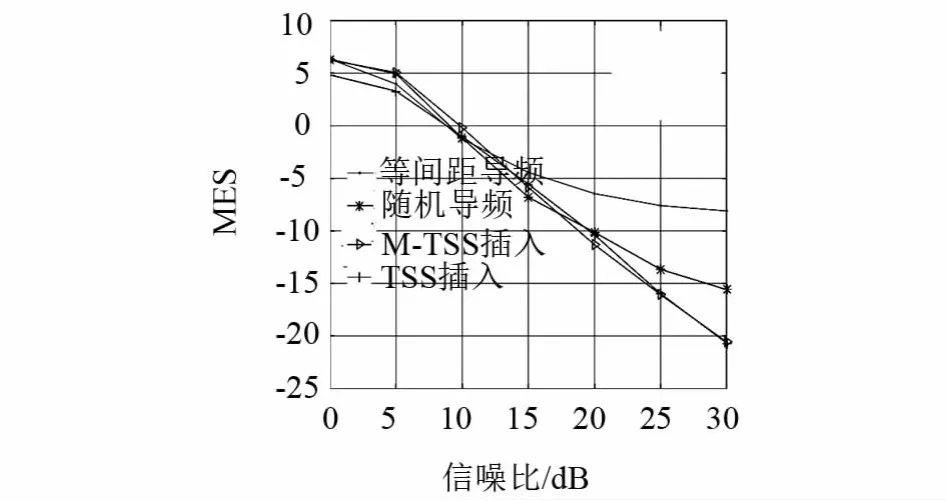
图8 导频为128时MSE仿真图

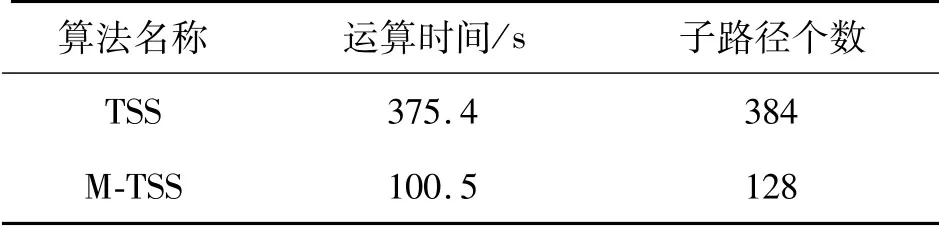
表4 导频为128时1次运行时间和子路径数比较

4 结束语

通过对室内可见光通信NLOS链路下的信道建模，利用信道稀疏性特征将信道估计技术同压缩感知恢复算法相结合，并提出了M-TSS算法.相较于TSS算法，改进算法不仅能够自适应选择子节点存活的个数，提高算法的灵活性，而且在运算复杂度上也具有优势.