基于泊松分布的遵义市暴雨、大暴雨次数概率特征

邹德全, 邹承立, 宋鑫民, 田洪进, 张云秋, 张开华

(贵州省遵义市气象局,贵州 遵义 563000)

0 引言

自进入工业化社会以来,全球海洋和大气逐渐变暖,极端降水事件发生的频次、范围及强度不断增加,极端降水事件和水文破坏对重要交通、水利和能源基础设施构成重大威胁[1-2]。贵州省遵义市处于云贵高原的东北部向湖南丘陵和四川盆地过渡的斜坡地带,地理位置介于27°08＇N～29°12＇N,105°36＇E～108°13＇E,国土面积30762 km2,属于亚热带湿润季风气候区。夏季受低值气压系统,西南季风和西太平洋副热带高压等天气系统影响,加之境内山高坡陡,河流纵横,短时强降水频发,山洪、滑坡、泥石流等灾害多发[3]。2014年8月11日,习水县局地特大暴雨,良村镇累计雨量达333.2 mm,出现连续6 h短时强降水,且连续2 h雨强超过60 mm·h-1,强降雨叠加特殊地形地貌,造成了严重山洪、滑坡、泥石流,导致财产损失惨重,因灾死亡13人。2019年6月21日务川特大暴雨,丰乐镇累计雨量达289.0 mm,导致洪涝灾害,直接经济损失19950万元。近年来,对遵义市暴雨的研究文献较多[3-7],都从天气学或者气候学角度着手。其实,从暴雨概率分布研究也有现实意义,尤其是在防灾减灾规划、应急管理方案制定方面更是如此。

某时段内暴雨(大暴雨)出现与否是一随机事件。概率分布理论是一切概率统计学方法最重要的理论基础,全面描述变量的随机性可用某种概率分布模式[8]。王颖等[9]使用广义极值分布研究重庆短历时极值概率特征,于新文等[10]采用泊松分布模型全面模拟中国东部地区暴雨频次分布特征,吕忠东等[11]、任至涵等[12]基于泊松分布分别对川东、成都经济区暴雨概率特征进行研究,而周其龙等[13]运用泊松概率分布模式揭示了黄河中下游地区的暴雨概率特征。本文将基于泊松分布,建立遵义市暴雨、大暴雨发生频率分布模型,并对遵义市暴雨、大暴雨进行模拟,得出暴雨、大暴雨出现概率特征的整体规律性及其空间分布特征。以希望为防灾减灾、应急管理部门提供决策参考。同时,该概率模式也可以为暴雨、大暴雨气候预测提供参考。

1 资料与方法

1.1 资料

所需基础降水日数据来源于贵州省气象信息中心共享服务网,时段为1961-2020年。

1.2 泊松分布方法

泊松分布(Poisson分布)是一种经典的描述稀有事件发生的概率模式,源于二项分布。当p→0,n→∞,且np=λ成为常数时的二项分布极限形式[8-13]。

假定某二项分布具有p→0,n→∞,即

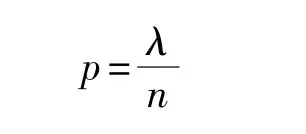
参数λ为正常数,当n→∞时,可得:

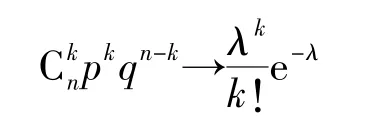
式中q=1-p,则服从泊松分布的随机变量X的概率分布为

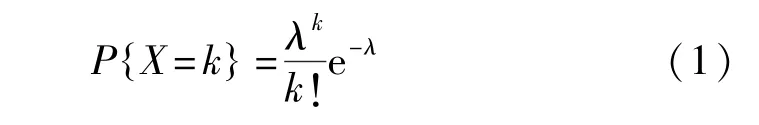
对于稀有事件X的各种可能取值X=0,1,2,3,…,则有

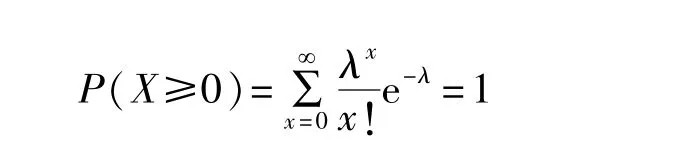
由此可以得到各种可能稀有事件发生次数的概率为

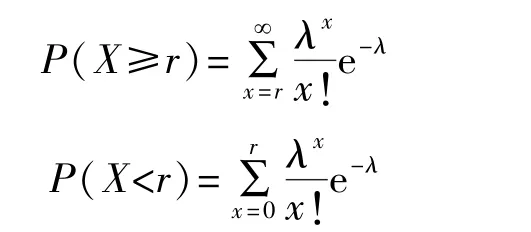
用递推还可得

又因为

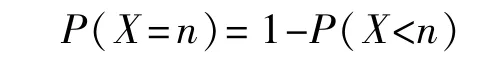
所以发生n次以上包含n次稀有事件概率为

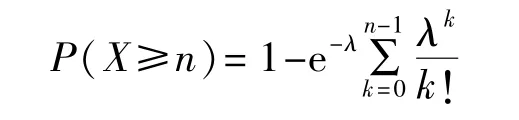
按照GB/T28591-2012国家标准《降水量等级》,分别统计出各县市区24小时≥50 mm暴雨和整体区域≥100 mm以上大暴雨次数。整体区域大暴雨次数取每年5-9月各县市区之和,各县市区暴雨次数取每年5-9月之和。每年5-9月有153天,时段为60 a,共计有9180 d。由此,暴雨日概率用时段内暴雨、大暴雨累计数除以9180估计。而泊松分布参数λ用时段内暴雨、大暴雨累计数除以60估计(表1、表2)。在此基础上,结合各站的参数λ和式(1)则可以建立起遵义市的暴雨、大暴雨Poisson分布模型。

表1 各县市区暴雨、整体区域大暴雨次数发生概率

表2 各县市区暴雨、整体区域大暴雨日数对应λ

进一步,由式(1)计算一年中发生k次暴雨、大暴雨概率P{X=k},则60 a应有60×P{X=k}个年份会发生k次暴雨,k=0,1,2,3,…,k时,可得发生的暴雨、大暴雨的理论年数。

从以上可见,各县市区暴雨概率、整体区域大暴雨概率均较小,而样本数n很大,粗略判断用泊松分布拟合是合适的。

2 结果分析

2.1 Poisson分布拟合及其效果检验

利用所得λ和式(1)建立各县市区暴雨、整体区域大暴雨泊松分布模型。经检验,各县市区暴雨次数及其整体区域大暴雨次数Poisson分布拟合均通过KS检验(显著性水平α=0.05)和χ2检验(显著性水平α=0.05),实测频数与理论频数的相关系数均在0.9以上(表3)。由此可见,遵义市各县市区暴雨频次、整体区域大暴雨频次均符合Poisson分布。

表3 各县市区(整体区域)发生k次暴雨(大暴雨)理论年数与实测年数相关系数

2.2 各县市区(整体区域)暴雨(大暴雨)频次总体分布特征

从建立的相应模型,结合时段(60 a)计算出各县市区(整体区域)发生k次暴雨(大暴雨)的理论年数(表4)。从表4可以看出,除仁怀市出现1次暴雨的概率最大外,其余11县市区均以出现2次概率最大,整体区域以出现3次大暴雨的概率为最大。各县市区暴雨集中在1～4次,整体区域大暴雨集中在2～5次,12个站实测频数与理论频数总体变化趋势一致。

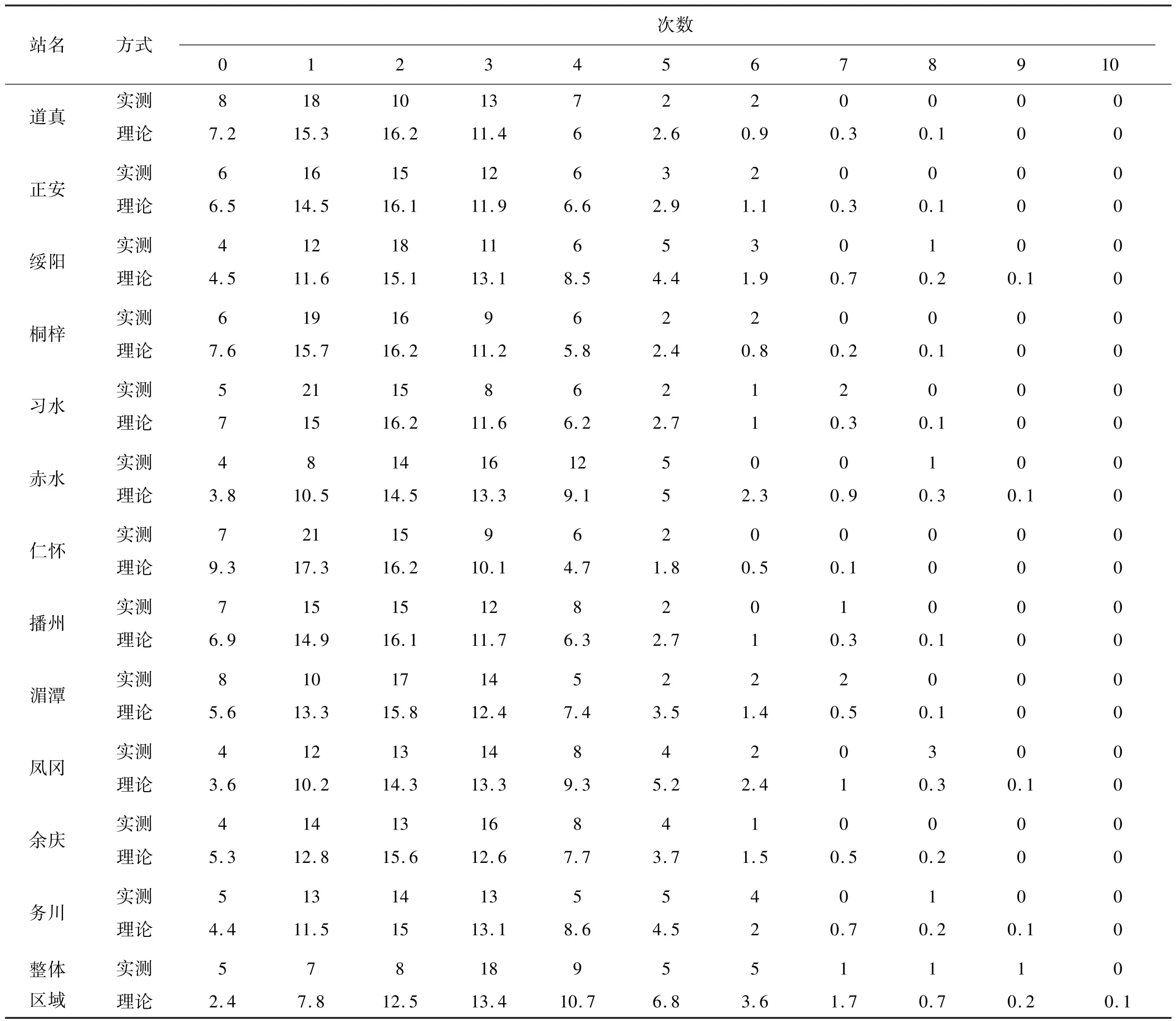
表4 各县市区(整体区域)发生k次暴雨(大暴雨)实测年数、理论年数

2.3 各县市区暴雨概率空间分布特征

表5为各县市区出现暴雨次数、整体区域出现大暴雨次数Poisson分布k次概率,表6列出各县市区年暴雨理论次数≥2次以上概率和整体区域年大暴雨理论次数≥3次以上概率。选择年暴雨≥2次以上理论概率为考察对象,讨论其空间分布。从图1看出,概率总体趋势自东向西减小,但西北部赤水、习水例外。东部、西北部概率较大,因而暴雨灾害风险较大;中部区域概率相对较小,因而暴雨灾害风险相对较小。整体区域每年≥3次以上概率为0.62。

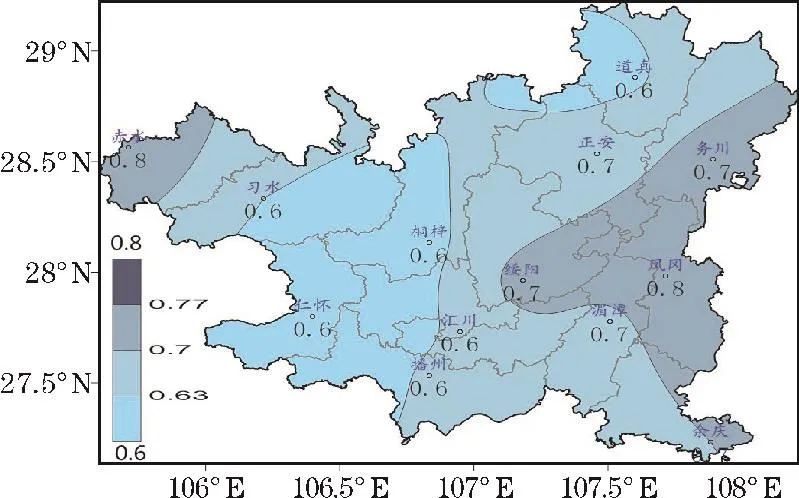
图1 遵义市每年出现≥2次以上暴雨的概率空间分布

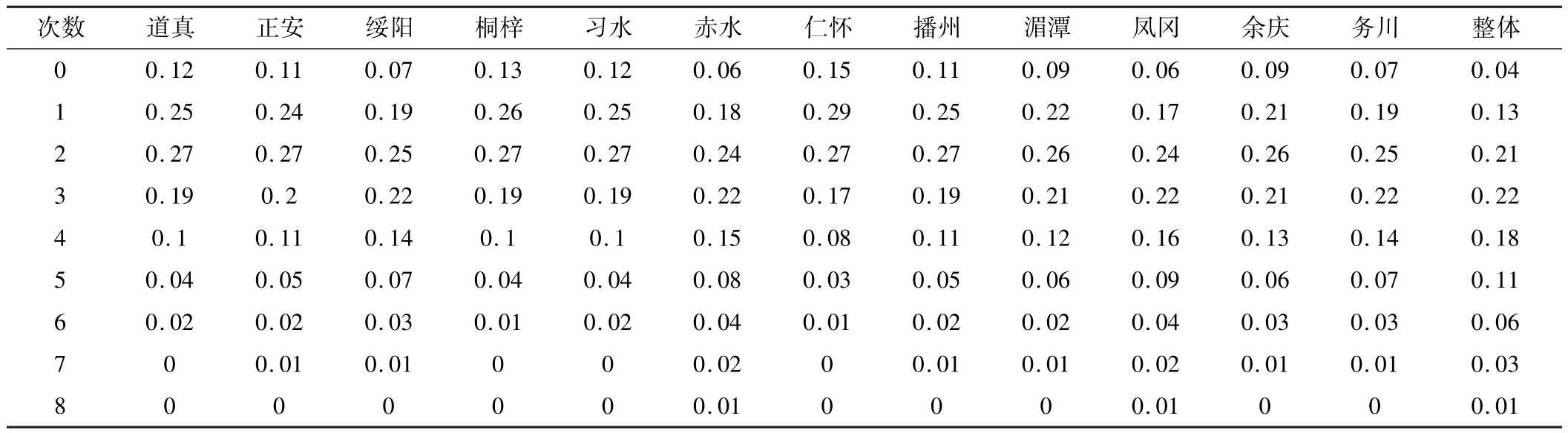
表5 各县市区暴雨次数、整体区域大暴雨次数Poisson分布k次概率

表6 各县市区暴雨(整体区域大暴雨)理论次数≥2次(3次)以上概率

3 结论与讨论

关于遵义市暴雨概率特征研究,采用信息扩散技术方法得出了各量级降水量出现概率,得出遵义短历时强降水气候频率是贵州省低值区之一,不是从极值分布理论上探讨遵义市暴雨、大暴雨出现次数的概率问题。描述稀有事件概率的Poisson分布是气象上广泛采用的方法。基于泊松分布分别对中国东部地区、成都经济区、黄河中下游地区的暴雨概率特征进行分析研究。本研究利用遵义市具有连续资料的12个县市区降水数据,建立整体区域大暴雨次数和各县市区暴雨次数Poisson分布模式,并且分析其概率变化特征。结果表明:(1)遵义市整体区域大暴雨次数、各县市区暴雨次数都符合Poisson分布。(2)遵义市整体区域每年≥3次以上大暴雨的概率为0.62,各县市区每年≥2次以上暴雨的概率在0.56～0.77。概率总趋势表现出自东向西减小,但西北部赤水、习水例外。东部、西北部概率较大,因而暴雨灾害风险较大;中部概率相对较小,因而暴雨灾害风险相对较小。

利用本研究建立的Poisson分布模式,还可以用于计算遵义市(各县市区)大于研究时段长度(60 a)出现的最大次数以上的大暴雨(暴雨)次数概率,对制定暴雨洪涝灾害防御规划、应急管理工作具有实际意义。