轻型木桁架齿板连接件的动态弹性模量测试研究

梁星宇， 宋利明， 高德伟， 周宇昊， 王 正*

(1.南京林业大学材料科学与工程学院，江苏 南京 210037；2.江苏金迪木业股份有限公司，江苏 泗阳 223700；3.南京林业大学机械电子工程学院，江苏 南京 210037)

随着建筑行业对木材及以木材为原料派生的各类木质复合材料的重视，轻型木结构建筑体系在许多国家盛行。单在北美地区，约有85%的多层住宅和95%底层住宅采用轻型木结构体系[1]。轻型木结构是利用均匀密布的规格材来承受房屋各种平面和空间作用的受力体系，其由木构架墙，木楼盖和木屋盖系统构成，适用于3层及3层以下的民用建筑[2]。由木构件组成的桁架，是木屋盖、木桥及木塔架的主要承重结构，用于木屋盖时通称为木屋架[3]。木桁架设计中最重要的一环便是节点设计。目前，木桁架节点连接方式有齿连接、钉连接、螺栓连接、齿板连接等[4]。其中齿板连接件具有较高的刚度和承载能力，被广泛用于由规格材制成的轻型木桁架节点连接或木构件的接长与接厚[5]。近年来，国内外研究者在木桁架齿板连接性能的相关研究方面取得了不少成果。2004年，Rakesh Gupta等探究了在风载荷和冲击载荷作用下采用齿板连接的木桁架节点处的性能，发现风荷载和冲击荷载使结构整体的刚度提高了约3倍，而对结构的强度和极限挠度则没有显著影响，研究者指出刚度的变化是由板齿附近木材的致密化引起的[6]。2007年，Ergun研究了红松采用不同齿板连接后制成的木桁架在节点处的承载能力，研究结果表明齿板的尺寸和齿的方向均对节点的承载能力有影响；节点处的承载能力与木材的弹性模量没有显著关系[7]。2012年，叶虹等通过对国产落叶松连接节点进行拉伸试验，探究了将国产材用于木桁架生产的可能性，并对齿板刚度和承载能力进行研究，提出了去除连接处板齿和加长边缘齿长等提高齿板节点性能的方案[8]。2016年，Villar等通过遗传算法对使用销钉和金属板连接的重型木桁架构件和节点进行优化，提出的模型结合了不同的变量，可以估算出在一定条件下桁架的最佳几何形状，横截面尺寸以及所需的连接件数量[9]。同年，丁星等研究了木节对受纯剪、拉剪、压剪3类试件的齿板连接延性比的影响。相关结果表明木节对这3类试件的延性比均值影响不大，在实际工程中，规格材的连接区域允许有一定尺寸的木节存在[10]。2017年，Liu等对采用齿板连接的木桁架腹杆的横向支撑可靠性进行了探究，相关结果表明：当相邻腹杆间的缝隙小于2 mm时，缝隙对齿板连接后结构平面外旋转刚度的影响可忽略不计[11]。2020年，Monzerrath等研究了由石梓木、柚木、墨西哥柏木用齿板连接后制成的不同跨度桁架的力学性能，研究结果表明桁架的承载极限值随跨度的增加而减小，且相比石梓木和墨西哥柏木，柚木制成的桁架具有更高的强度和刚度[12]。

由上述研究可知，刚度性能是采用齿板连接木桁架性能研究中的重点。对于木桁架的下弦杆，刚度研究有助于确保屋盖楼盖刚度可靠性及其房屋的整体寿命。鉴于此，本研究运用动力学理论，通过瞬态激励法，测量SPF锯材制成的单杆和经齿板连接后得到的组合杆在自由梁约束条件下的基频值，并算得其基频的动弹性模量值。有助于为我国锯材、规格材领域内的无损检测工作提供有效借鉴。此外，通过对木桁架的检测和评估，系统总结出一套木桁架动弹性模量的评估方法，具有迫切的现实意义。我国在这方面的研究和实践投入较少，在这方面的基础研究工作非常薄弱，生产、设计和制造技术都处在发展的初步阶段，与国外仍有一定的差距，所以开展对木桁架动弹性模量研究，有利于发展我国的木桁架，有利于我国现代木结构建筑设计研究。

1 轻型木桁架系统动弹性模量测试

1.1 测试对象与仪器

1.1.1 测试对象

本研究测试了用于轻型木桁架下弦杆的单杆和组合杆，其材料为SPF(云杉-冷杉-松)。SPF盛产于加拿大的软木林，该树种组合因其直度、强度重量比、可加工性、价值及可用性，成为建筑业最为广泛采用的树种组合。单杆尺寸为3 600 mm(L)×90 mm(b)×40 mm(h)，含水率为7%～8%，气干密度为0.42～0.48 g/cm3。组合杆由两根单杆通过齿板连接组合而成，如图1所示。具体组合方式为：1号和2号杆组合，记为13号杆；3号和4号杆组合，记为14号杆；5号和6号杆组合，记为15号杆；7号和8号杆组合，记为16号杆；9号和10号杆组合，记为17号杆；11号和12号杆组合，记为18号杆。本研究采用齿板连接件由镀锌钢板经单向打齿制成，尺寸为150 mm×80 mm×5 mm，重量为210 g。单杆和组合杆的具体规格如表1所示。

图1 单杆组合示意图

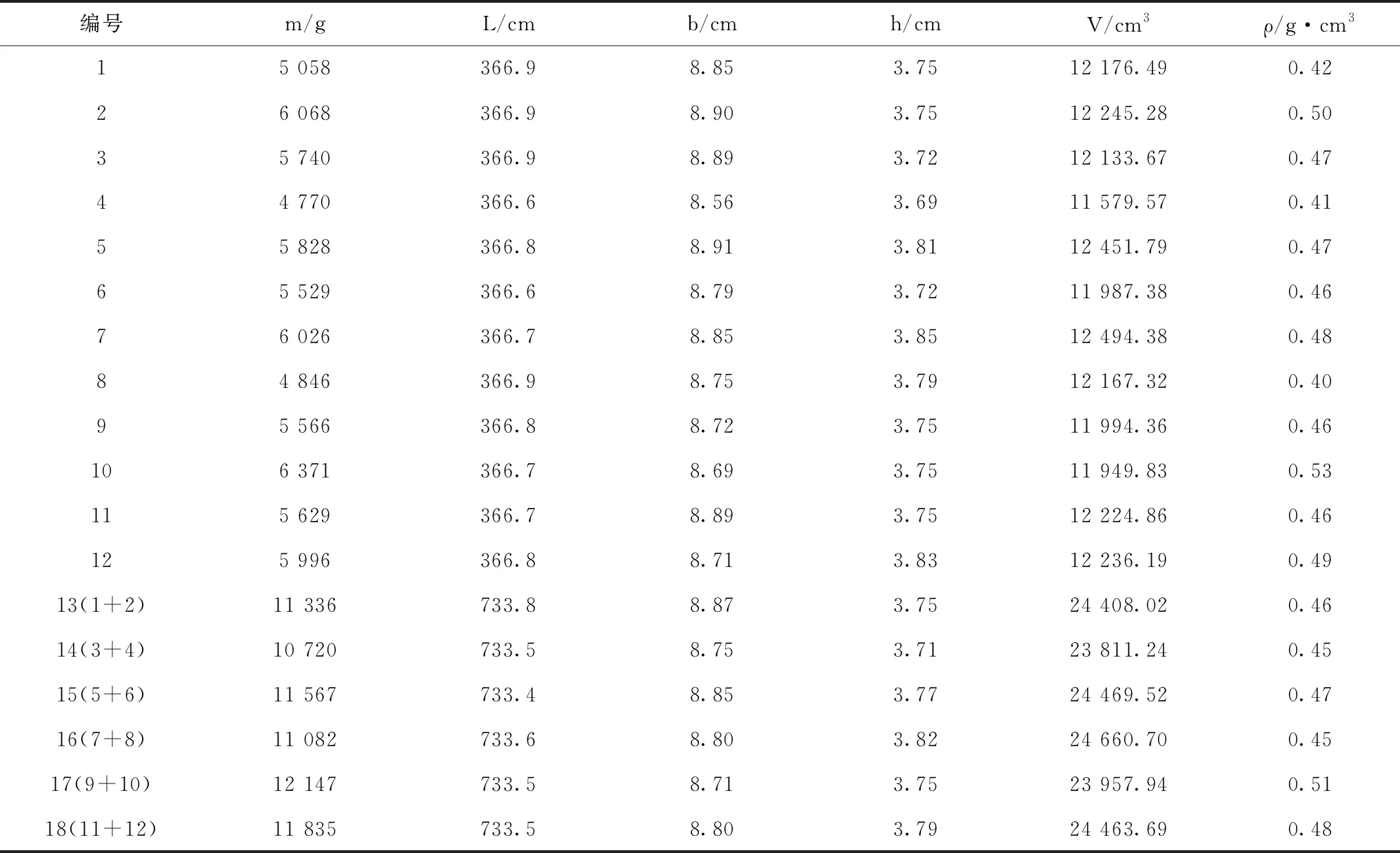
表1 测试杆件规格表

1.1.2 测试仪器与工具

CRAS振动及动态信号采集分析系统1套，主要包括激振器；AZ804-B型信号调理仪；AZ308型信号采集箱；CRAS软件及计算机；CA-YD-126型加速度计2只，其灵敏度因子为49.7 pc/n；橡胶锤1把；弹性绳。

1.2 测试原理

本研究采用机械动力学的瞬态激励法，其频响函数为输出的傅里叶变换与输入的傅里叶变换之比。具体的动弹性模量测试方法是：以力锤敲击设置有加速度计的木桁架杆件；把加速度计检测的杆件反应加速度G送入信号调理箱经放大、滤波后输出，再送入信号采集箱内进行数据采集；经模数转换后进行数据处理。

首先，实现轻型木结构桁架杆件测试系统的动态信号调理箱和采集箱上的单通道或双通道(CH1、CH2均为加速度计通道)的测量连接。通过加速度计接受机械信号并将其变为电信号，再经信号调理仪放大、滤波后，对其进行信号的A/D集及谱分析，从H1频谱中可以得出杆件的阶次频响函数谱。

在自由梁的约束条件下，通过横向与竖向振动法测得试样的一阶固有频率。根据理论公式(1)计算出杆件动弹性模量的值[13]：

(1)

式中：E为试样动态弹性模量，Pa；ρ为气干密度，g/cm3；f1为第一阶固有频率，Hz；L为试样长度，mm；h为试样厚度，mm。

1.3 测试过程

按图2～图5连接各仪器和杆件。测试时试样分为横置(L×b×h)和纵置(L×h×b)两种放置方式。测试单杆时，将1只加速度传感器牢固安装在杆件上，接受响应信号(CH1)。在振动信号的采集参数设置上，采用H1或1/H1模式；CH1单位设为mm/s2。测试用齿板连接的组合杆时，将2只加速度传感器分别牢固的安装在杆件上，接受响应信号(CH1)和(CH2)。在振动信号的采集参数设置上，采用H1或1/H1模式；CH1和CH2单位都设为mm/s2；负触发为1的触发电平为5%，且触发延迟为-20；信号放大倍数为100；分析频率为1 000 Hz。为防止频率混迭，试验选择低通滤波器的频率上限，滤波频率设为1 000 Hz；实测前，进入示波方式，连续敲击杆件，以检查仪器连接线是否接通，波形是否合理等，不合理时将重新设置；正式测量时，通过用带塑料头的力锤敲击杆，激起柱体系统振动，以触发方式采集数据，进行动态信号频谱分析，并在和H1频谱中读出杆的第1阶、第2阶固有频率值。

图2 单杆横置测试系统示意图

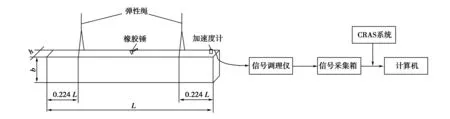
图3 单杆纵置测试系统示意图

图4 组合杆横置测试系统示意图

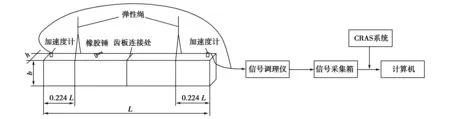
图5 组合杆纵置测试系统示意图

2 结果与分析

2.1 单杆测试结果

通过瞬态激励法分别对横置和纵置的12根单杆进行测试，得到一阶频率图谱如图6和图7所示。为了保证测试结果的准确性和合理性，对每根下弦杆进行了多次测试，取其中频谱显示较好的一组数据。12根单杆测试结果见表2。

表2 单根下弦杆测试结果表

图6 4号杆横置一阶频谱图

图7 1号杆纵置一阶频谱图

由表2可知单杆横向放置时测得的一阶固有频率平均值为13.98 Hz，纵向放置时测得的一阶固有频率平均值为32.35 Hz；纵向放置时测得的一阶固有频率平均值约为横向放置时的2.3倍。单根下弦杆横向放置时测得的动弹性模量平均值为10.94 GPa；纵向放置时测得的动弹性模量平均值为10.82 GPa；两种放置方式测得的动态弹性模量平均值均在10.9 GPa左右，但横向放置测得的动态弹性模量平均值比纵向放置时测得的值大1.1%；横向和纵向放置时测得的动态弹性模量值的变异系数分别为12.5%、13.3%，均小于15%，说明试验数据可靠。

2.2 组合杆测试结果

将12根单杆通过齿板连接件进行组合后，分别对横置和纵置的6根组合杆进行测试，得到一阶频率图谱如图8和图9所示。6根组合杆测试结果见表3。

表3 组合杆测试结果表

图8 1+2号组合杆横置一阶频谱图

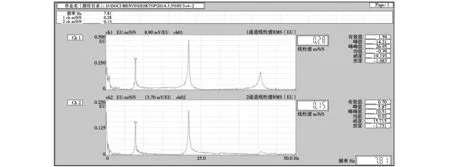
图9 3+4号组合杆纵置一阶频谱图

由表3可知组合杆横向放置时测得的一阶固有频率平均值为3.37 Hz，纵向放置时测得的一阶固有频率平均值为7.84 Hz；纵向放置时测得的一阶固有频率平均值值约为横向放置时的2.3倍。组合杆横向放置时测得的动弹性模量平均值为10.34 GPa；纵向放置时测得的动弹性模量平均值为10.24 GPa；两种放置方式测得的动态弹性模量平均值均在10.3 GPa左右，但横向放置测得的动态弹性模量平均值比纵向放置时测得的值大1.0%；横向和纵向放置时测得的动态弹性模量值的变异系数分别为10.5%、8.1%，均小于15%，说明试验数据可靠。

2.3 测试结果分析

2.3.1 放置方式对杆动弹性模量的影响

由表2将各单杆按两种不同放置方式测得的动态弹性模量数值进行对比，得到如图9所示的对比图。由表3将各组合杆按两种不同放置方式测得的动态弹性模量数值进行对比，得到如图10所示的对比图。

图9 单杆横置和纵置动弹性模量对比图

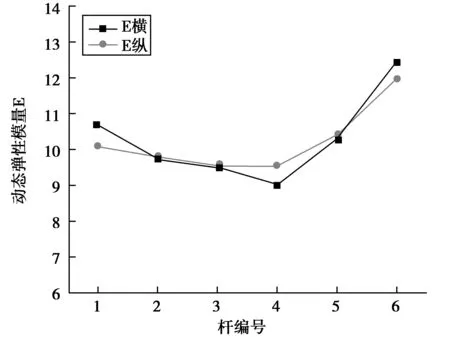
图10 组合杆横置和纵置动弹性模量对比图

由图9和图10得知，本研究中各单根和组合杆按两种不同放置方式测得的动态弹性模量值基本吻合，即不同放置方式对本研究所采用的动力学测试方法得到的动弹性模量值影响不大。

2.3.2 齿板连接件对杆动弹性模量的影响

综合表2和表3可知杆组合前后动态弹性模量的变化，如表4所示。杆组合前后横置和纵置时测得的动弹性模量值对比如图11和图12所示。

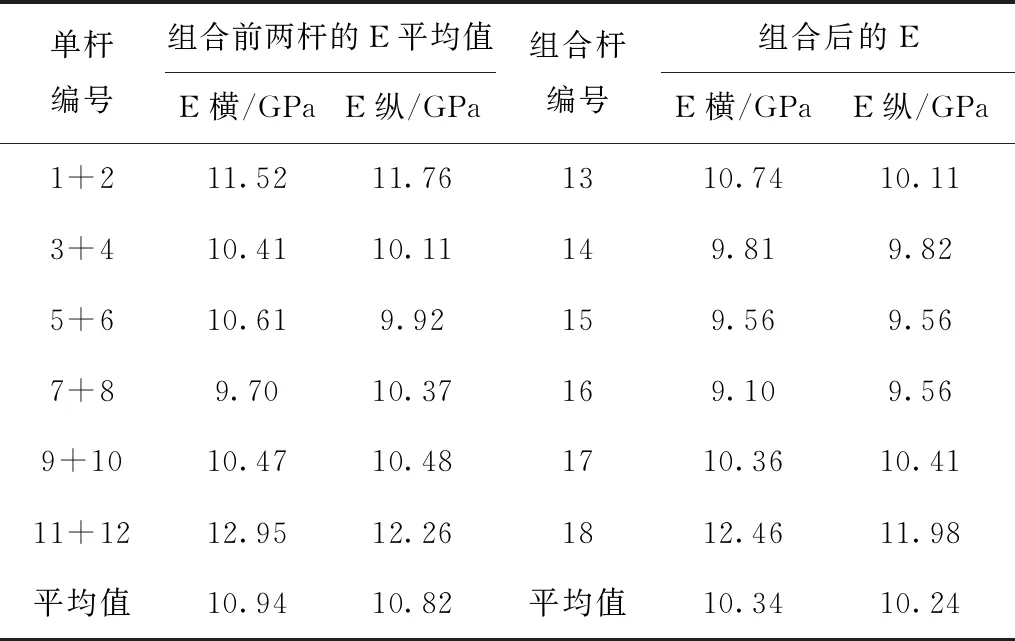
表4 杆组合前后动弹性模量对照表

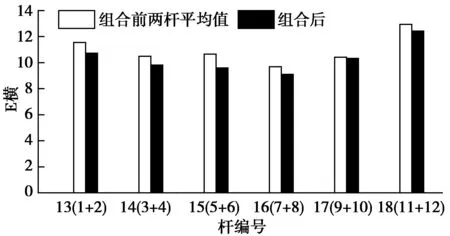
图11 横置杆组合前后动弹性模量对比图

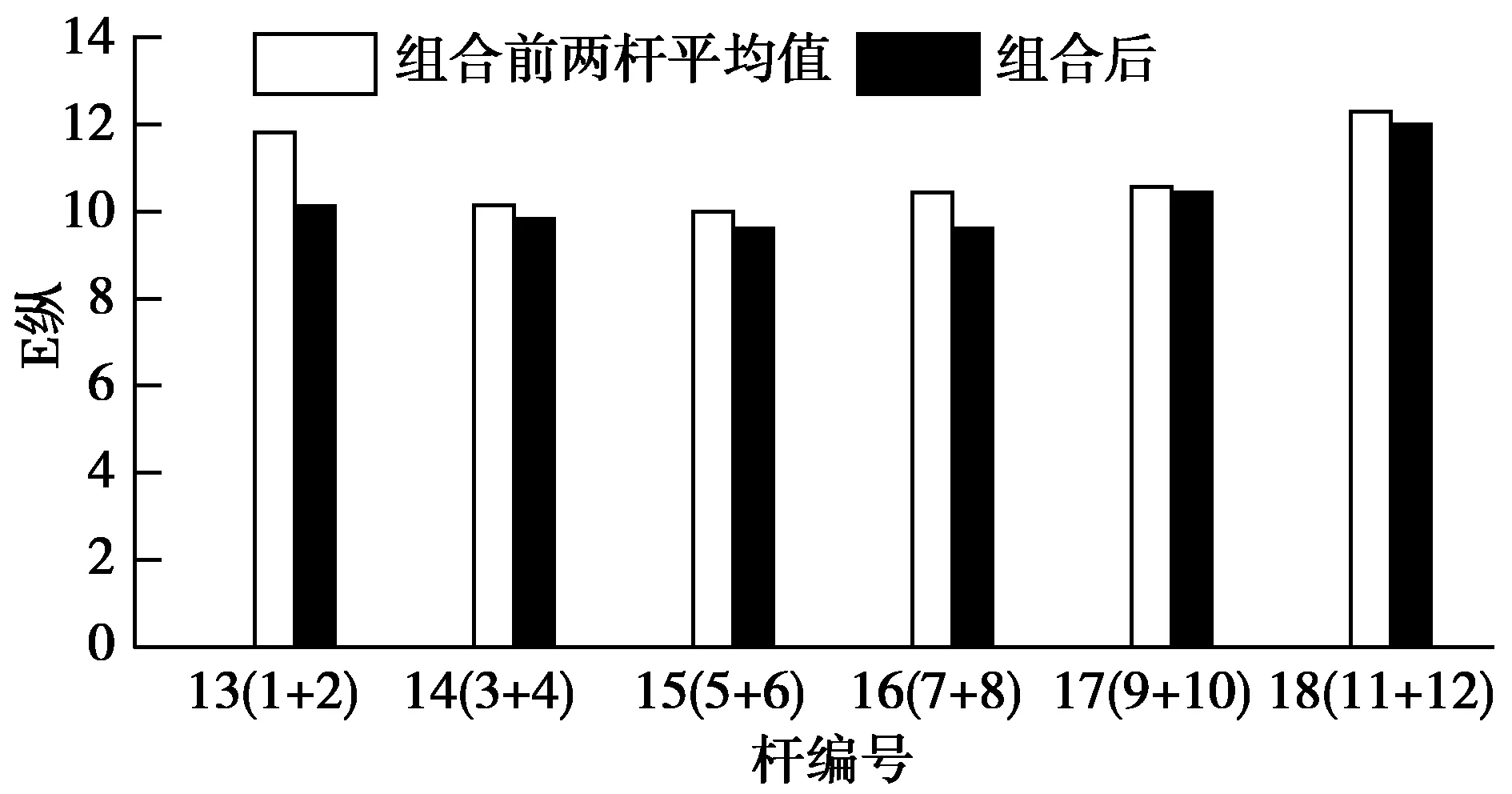
图12 纵置杆组合前后动弹性模量对比图

由表4可知，两杆组合前的动弹性模量平均值约为10.9 GPa，经齿板连接件组合后的动弹性模量平均值约为10.3 GPa；组合后杆动弹性模量值下降了约5.5%，可见齿板连接降低了结构整体的刚度。结合表4、图11和图12可知，每组杆的动弹性模量值在组合后都有不同程度的降低，进一步验证了齿板连接对结构刚度的作用。在实际使用中设计人员和工程师应考虑到这种变化，以提供可靠的结构刚度。

3 主要结论

(1)本研究中对用于轻型木结构木桁架下弦杆的单杆，横向放置测得的动态弹性模量平均值比纵向放置测得的值大1.1%；对经齿板连接后的组合杆，横向放置测得的动态弹性模量平均值比纵向放置测得的值大1.0%。对于本研究所采用的动态测试方法，杆件横向放置和纵向放置测得的动态弹性模量值基本一致，即不同放置方式动弹性模量的测量影响不大。

(2)本研究中两根单杆在组合前的动弹性模量平均值约为10.9 GPa，经齿板连接件组合后的动弹性模量平均值约为10.3 GPa，下降了5.5%，即齿板连接降低了结构整体的刚度，在工程实际中要考虑到这一变化，提高结构刚度的理论设计值。

(3)研究所使用的试验操作快捷简单，测试所得动弹性模量值的变异系数均满足要求。说明本试验所采用的机械动力学测试方法及相关测试仪器，具有操作简便、工程应用性强、数据可靠性高等特点。