含沟槽缺陷铜镍合金管爆裂压力计算

潘兴隆，张 攀，张鲁君，贺 国

(1.海军工程大学 动力工程学院,武汉 430033；2.92785部队，河北 秦皇岛 066200；3.91878部队,广东 湛江 524300)

铜镍合金材质因优秀的防污性能与耐腐蚀性能大量应用于舰船海水管系[1]。海水管系长期服役过程中，海水温度、溶氧量、含砂量、流速及海洋生物活动等诸多因素联合造成管内腐蚀[2-3]，腐蚀的存在威胁管道正常运行与主机运转。评价腐蚀后铜镍合金管路的爆裂压力是管路状态评估与科学维修的依据。

近40年来，国内外学者与组织先后提出ASME B31G标准[4]、DNV RP-F101规范、PCORRC方法等诸多评价标准并据此构建了相对完善的评价体系，但该评价体系集中于油气运输用各级管线钢[5]。因油气运输管路多为大口径钢管，评价时一般将管路假设为薄壁管路，忽略了壁厚方向径向应力的影响。铜镍合金管往往口径较小且管壁相对较厚，在材料力学中划属厚壁管路[6]，径向应力不可忽略，因此该材质管路的评价可参考现有评价体系但需要修正。Chiodo[7]和帅健[8]使用有限元方法结合爆破试验实例，验证了非线性有限元法的效果。但现有文献在使用有限元方法时基于塑性极限的失效模式做静力学求解，未能完全展现韧性材料的性能。

本文基于DNV RP-F101许用应力法[9]，建立含修正函数的铜镍合金管爆裂压力预测公式，修正壁厚和材料性质的影响。基于塑性失效的失效模式，对爆裂过程做数值模拟并使用最小二乘法求解修正函数，最后通过试验验证数值模拟分析结果及预测公式的正确性。

1 爆裂压力预测公式

1.1 应力分析

处于稳定工作状态下的铜镍合金材质海水管系，工作载荷为海水对管路内壁的压力，同时管体也会受到安装载荷、冲击载荷、振动载荷的作用。内压为管路主要承受载荷，其他载荷对海水管系的作用相比内压较小。在此忽略其余载荷对海水管系的作用，将处于稳定工作状态下的海水管系视作仅受内压作用的厚壁圆筒。管路一般较长，可视为轴向无限长管道。铜镍合金材质应用在海水管系时，管路口径一般较小，径厚比小于20(D/t≤20)，划属厚壁管路，壁厚引起的径向应力不可忽略。

首先对不含缺陷的管道(无损管道)进行受力分析，如图1所示。假设沿管道轴线变形为零，上述问题可以转化为平面应变问题，当管道为厚壁管路时，认为壁厚方向存在应力梯度。在弹塑性范围内管壁上任一微元其三向应力表述为[10]

(1)

式中：σθ、σr、σz分别为管路的环向应力、径向应力和轴向应力；Ro、Ri为管路的外半径和内半径；p为管路的内压，ρ为微元半径。

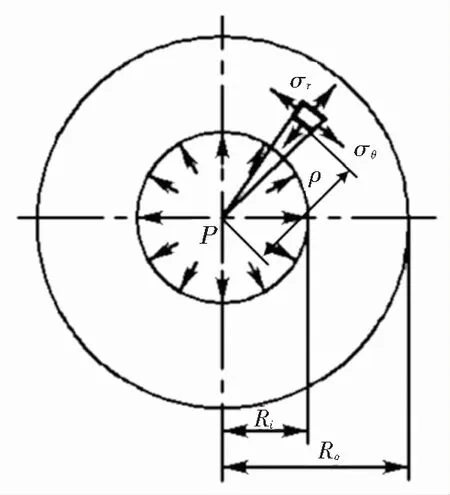
图1 无损管道应力分析Fig.1 Stress analysis of no-defect pipeline

若管道为薄壁管路，则在式(1)中径向应力为零(σr=0)，这也是现有评价标准中做的假设。管道在加载持续增大内压时，管道将经历弹塑性变形直至爆裂的过程。公式(1)中描述三向应力的适用范围为管道弹性变形直到外壁达到屈服(塑性力学中描述的塑性极限状态)，在管道所有点均达到屈服后，应力不仅与应变有关，还与变形历史有关，塑性状态具有极强的非线性，爆裂压力无法得到解析解。径向应力的影响只能采用修正函数的方式表达。各级管线钢的强度评价标准应用于铜镍合金管时的误差一并通过修正函数修正，修正函数由数值模拟方法求得。

1.2 DNV标准及预测公式

DNV RP-F101许用应力法是基于许用应力设计的形式，该计算公式形式简单，使用方便。该方法评价只有内压作用的腐蚀管道时，失效压力计算公式为[9]

(2)

式中，pf、p0分别为腐蚀管道、无损管道的失效压力；R为缺陷影响因子；σb为管材的抗拉强度；t为完整管壁厚度；D为管道公称直径；d为腐蚀深度；M为腐蚀长度修正系数；LZ为腐蚀缺陷轴向长度。

DNV OS-F101标准[11]将管道的极限状态划分为服役极限状态(SLS)、最终极限状态(ULS)、疲劳极限状态(FLS)和偶然极限状态(ALS)，爆裂状态属于最终极限状态，该标准给出的无损管道爆裂极限状态压力公式为

(3)

式中：pb0为无损管道的爆裂压力。观察式(2)和式(3)，p0和pb0相差极小，故可将管道失效压力近似认为爆裂压力。

壁厚方向径向应力的影响通过修正函数ν修正，ν与腐蚀深度比N(N=d/t)有关，如下式表述：

ν=ν(N)

(4)

基于DNV准则建立通海管路爆裂压力预测公式，该公式由腐蚀管道失效压力项pf和修正函数ν(N)组成。综上所述，含内腐蚀缺陷铜镍合金管道爆裂压力预测公式pb可表述为

(5)

2 数值分析

2.1 有限元设置

复杂的海洋条件导致铜镍合金管的腐蚀，缺陷一般以金属损失的形式出现在管内，且形状呈无规则状。强度评价的前提是缺陷尺寸可测量，因此，首先应将不规则腐蚀缺陷模型化为规则缺陷。一般可简化为均匀矩型、沟槽型、球型3种[12]，以沟槽缺陷为例，研究其缺陷强度，模型如图2所示。

图2 1/2沟槽型缺陷模型Fig.2 Half groove defect model

假设通海管路所用铜镍合金材料为各向同性材料。根据管材供应厂家提供的性能测试数据，将力学性能数据中的名义应力应变转变为真实应力应变：

(6)

式中：Bo、Lo分别为标准拉伸试件的初始截面积和标距；B、L分别为标准拉伸试件在拉伸变形过程中的实际横截面积和标距；σ、ε为单轴拉伸试验得到的工程应力应变；σ′、ε′为真实应力应变。

铜镍合金管屈强比低、延展率大，无明显屈服点[13]，故本构关系选择Ramberg-Osgood幂硬化模型，其表达式为

(7)

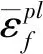
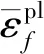
(8)

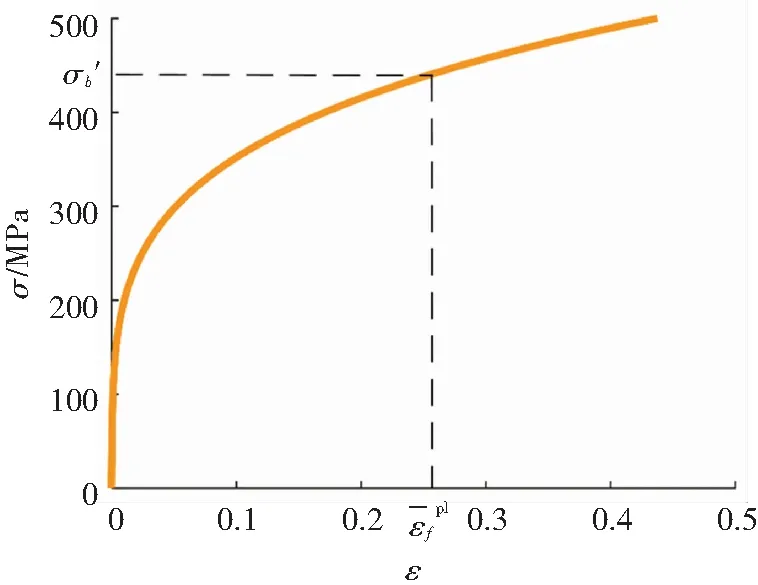
图3 R-o本构模型Fig.3 R-o constitutive model

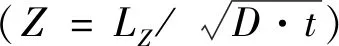
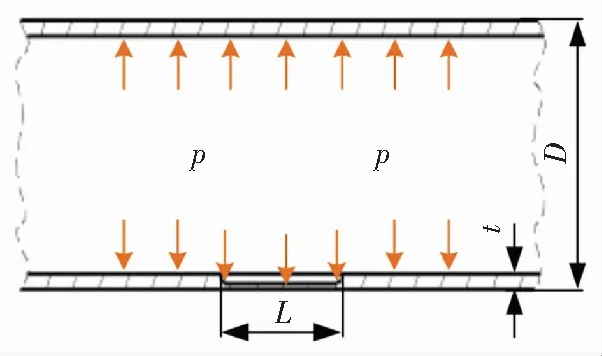
图4 压力加载范围Fig.4 Pressure loading range

表1 管道编号表Tab.1 Numbering for corrosion pipelines

2.2 爆裂过程及特点分析

图5展示了编号为G17的管道在内压作用下爆裂的过程云图。开始加压后，缺陷处出现应力变化，表现为缺陷处环向两侧为高应力区，轴向两侧为低应力区。随着管道加载压力的增大，缺陷中央处表现出明显的应力集中，从弹性变形到进入塑性流动阶段最后抵达抗拉极限。从图5(d)可以看出缺陷中央应力云图开始收缩，表明此时已经存在单元进入应力退化阶段，且应力退化从缺陷最中央区域开始。图5(e)缺陷处沿壁厚方向已全部完成应力退化，发生颈缩后管道将突然爆裂，出现沿管道轴向的巨大裂口。

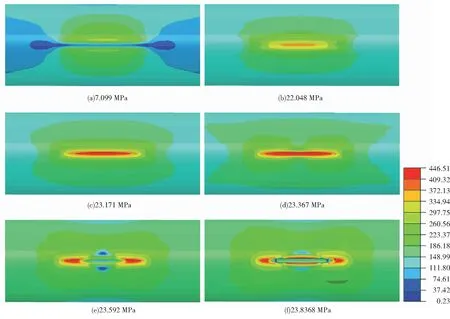
图5 G17不同内压下等效应力云图Fig.5 Von Mises stress nephogram of G17 under different internal pressure

图6展示了在管内压持续增长下，缺陷中心处沿壁厚方向三个点的Von Mises应力和等效塑性应变情况，其中(b)图为(a)图黑色矩形区域放大图。在塑性流动后期，内壁点、中间点与外壁点Von Mises应力依次度过抗拉极限开始应力退化并迅速达到断裂条件。G14#管路剩余壁厚较厚，在同一内压时，内壁点应力退化结束后单元已失效，中间点Von Mises应力才达到损伤萌生界限开始应力退化。换言之，内壁点、中间点和外壁点依次在很短的压力区间内失效，在图3.6(b)中表现为应力曲线与应变曲线集中交织，宏观上表现为脆性断裂。G20#管路剩余壁厚相比较薄，管路壁厚方向上单元应力均度过抗拉极限开始应力退化后，内壁点、中间点与外壁点等效塑性应变才逐渐增加至断裂标准，因此断裂时将表现出塑性。由此可得虽然均为厚壁铜镍合金管路，但是剩余壁厚较薄时表现为塑性断裂，剩余壁厚较厚时表现为脆性断裂。

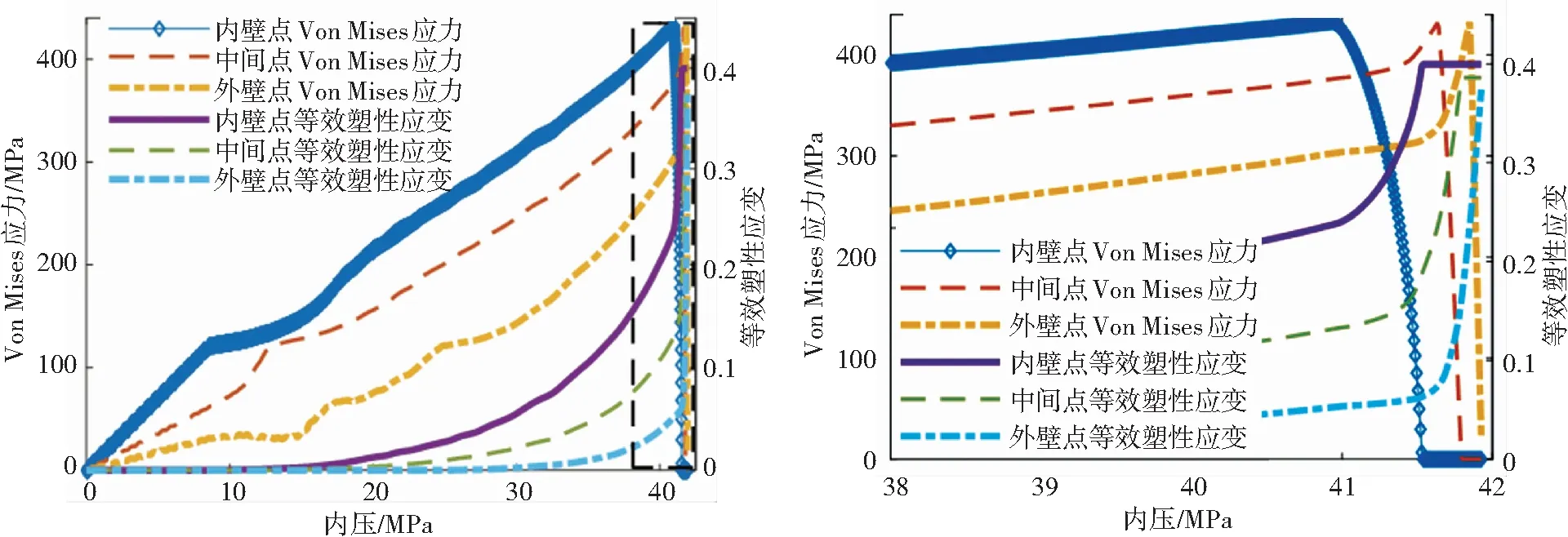
(a)G14

2.3 缺陷参数对爆裂压力影响

Netto[13]指出腐蚀缺陷宽度(环向角度)在腐蚀深度不够深时对失效压力影响很小，本文不予讨论。下文探究时将设置腐蚀宽度为固定值，依据表1探究缺陷形貌参数对爆裂压力影响。

腐蚀缺陷深度比与爆裂压力的关系如图7(a)所示。爆裂压力随腐蚀深度增加呈负线性下降，说明腐蚀深度是影响铜镍合金管爆裂压力的重要因素。且轴向长度越大，腐蚀深度对爆裂压力的影响效力越强。当腐蚀深度达到通海管路壁厚的80%大小时，铜镍合金管的爆裂压力已不足原承载能力的30%。

腐蚀缺陷轴向长度比与爆裂压力的关系如图7(b)所示。失效压力随腐蚀轴向长度呈指数型式下降。腐蚀缺陷轴向长度在Z<4时对爆裂压力影响很大，但随着轴向长度的增大，爆裂压力变化曲线趋于平缓；超过一定长度时，失效压力趋于稳定值，说明腐蚀缺陷轴向长度对通爆裂压力的影响随着轴向长度的增加效力逐渐减弱，且腐蚀深度越深，效力减弱的速度就越慢。

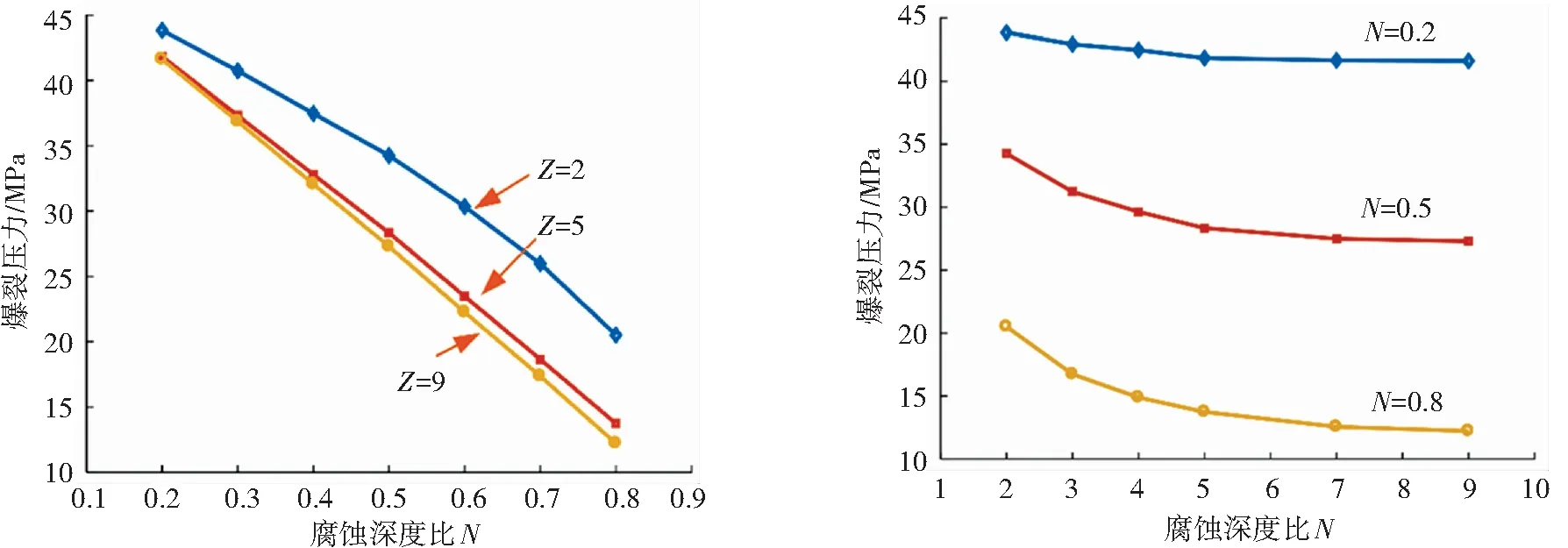
(a)腐蚀深度与爆裂压力的关系 (b)腐蚀长度与爆裂压力的关系图7 缺陷参数对爆裂压力影响Fig.7 Influence of defect parameters on burst pressure

2.4 修正函数的求解

使用有限元方法研究了各腐蚀深度与长度下管道爆裂压力之后，对比DNV RP-F101准则结果，发现随着缺陷深度增加，公式与数值模拟结果误差先减小后增大，如表2所示。证明壁厚方向径向应力的影响是存在的，且可通过上文引入的v(N)修正。使用v(N)将公式(5)的值向数值模拟结果逼近。

修正函数v(N)需要满足连续性函数，因此选择将修正函数定为下面形式：

(9)

以有限元结果与修正公式的差值平方和e(r)作为优化目标

(10)

运用最小二乘法，以x=[x1,x2,x3]T作为设计变量，当e(r)值最小时，认定这组设计变量拟合效果最优。以表2数据为样本，得最优一组设计变量为x=[765.18 46.55 884.48]T。据此可写出修正后的预测公式

(11)

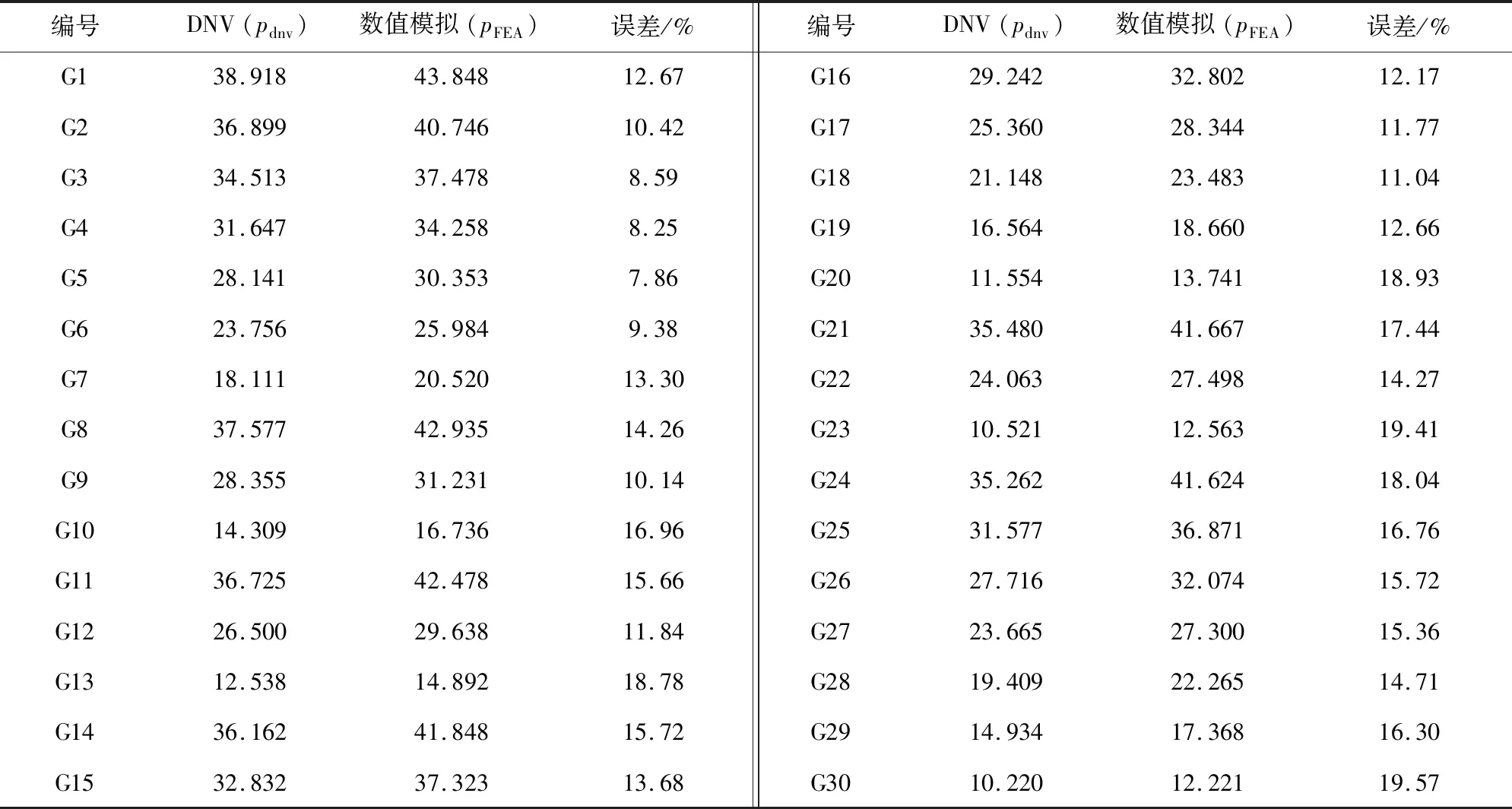
表2 DNV标准与数值模拟结果对比Tab.2 Contrast of DNV standard and numerical simulation results

3 试验验证

3.1 试件制备与试验方法

现有文献的腐蚀缺陷制作集中在管外壁，内腐蚀缺陷的制作是需重点克服的难题[14-15]。在对比化学腐蚀、电腐蚀、机械加工三种缺陷制作方法的优缺点后，选择机械加工制造内缺陷。

所进行爆破试验最高压预计达40 MPa，属于超高压容器爆破，因而试件工装必须牢固可靠、密封必须在超高压下依然效果良好，确保爆破时仅从缺陷区域爆开。先后试验了焊接密封、螺纹密封、法兰密封3种密封方式确认法兰密封具有优秀的密封性能，可以可靠承压。法兰密封方法如下：首先在试件两端各焊接铜法兰，要求焊接牢固；再以铜法兰为固定点，将钢制法兰用高强螺栓压紧在试件上，试件与钢制法兰的接触面上衬橡胶垫片。要求缺陷部位远离焊接区域，避免焊接热影响区对管材性能产生影响。

在试件缺陷处外表面粘贴应变片采集管道在管内压力作用下鼓胀时的应变情况，在注水口出口处与高压软管之间同时加装压力传感器和压力表，两者互为验证、补充(图8)。应变信号与压力信号传输至信号采集系统，记录压力与应变时间历程。试验参照GB/T 241-2007《金属管液压试验方法》执行[16]。

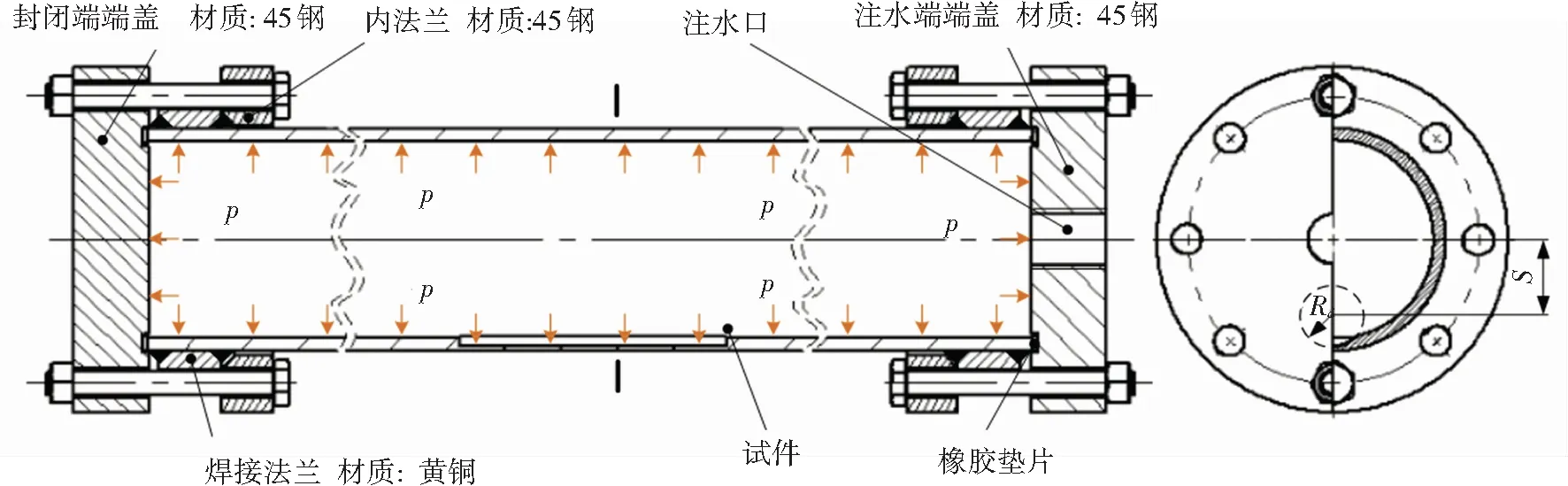
图8 试件工装Fig.8 Specimen tooling

3.2 试验结果

3.2.1 裂口形貌验证

试件在静水压下按照预计在加工缺陷处爆裂，缺陷处环向一圈均出现鼓胀，且缺陷处鼓胀最显著；沿管轴线方向出现线形裂口，裂口外张，长度比加工的沟槽缺陷长度稍短一些。图9展示了仿真与试验对比结果，图9(a)中可观察到的缺陷区域局部鼓胀和巨大线性裂口均能在图9(b)、9(c)仿真中找到对应的形貌，证明仿真模拟结果与实验结果吻合。

图9 管路裂口形貌对比Fig.9 Contrast of pipe fracture morphology

3.2.2 爆裂特点验证

将爆裂后试件缺陷区域割开，研究其断面宏观形貌。图10(a)是剩余壁厚为3.5 mm的试件，断裂面呈晶粒状，断口平齐，断口边缘没有剪切唇，为明显脆性断裂特征；图10(b)是剩余壁厚为1.5 mm的试件，断裂区域周围产生明显塑性变形，断裂面边缘可见剪切唇。该结果验证了2.2节中数值模拟结论吻合。

3.2.3 预测公式验证

通过静水压爆破试验验证有限元方法拟合出来的公式的准确程度。对进行的三次试验所使用缺陷管路进行编号，依次编号为G31、G32、G33。根据DNV RP-F101准则，可得到一组公式解；分析测试系统和压力表数据，可得试验爆裂压力，将以上两者数据汇总，见表3。将腐蚀长度比Z为5时DNV公式计算值，预测公式值，爆破试验结果做以对比，如图11所示。由图可知，预测公式准确性比DNV公式要高，修正效果较好。

(a)脆性断裂 (b)塑性断裂图10 断裂宏观形貌对比Fig.10 Macroscopic morphological contrast of fractures

表3 沟槽缺陷管路爆破结果对比

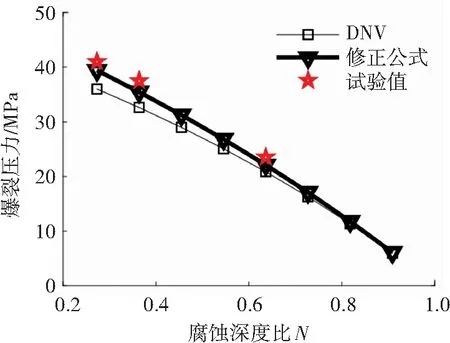
图11 含沟槽缺陷管路试验数据验证Fig.11 Test data validation of groove defect pipelines

4 结 论

本文对铜镍合金管爆裂压力做了理论分析、数值模拟、试验研究，得到以下结论：

1)对于含沟槽型内腐蚀缺陷的厚壁铜镍合金管道，修正了其爆裂压力预测公式，试验证明预测准确度相比DNV公式更优，保守程度更低。

2)对仅受内压作用下的铜镍合金管道爆裂过程进行了数值模拟，对比爆破试验可知，数值模拟得到的裂口形貌与试验结果高度相似，证明数值模拟效果较好。

3)通过分析数值模拟结果，结合试样爆裂后形貌分析，得到剩余壁厚较小时管道爆裂表现为塑性断裂，剩余壁厚较大时管道爆裂表现为脆性断裂的结论。

4)对含沟槽型缺陷管道，腐蚀深度对管道爆裂压力起决定性作用，两者呈负线性相关；腐蚀长度在深度较小时对爆裂压力影响不大，在深度较大时两者呈负指数性相关。