钛合金梁式管接头密封性能的结构优化设计

崔 颖，于颖嘉，张宏翔，钟兢军

(1.大连海事大学 船舶与海洋工程学院，大连 116026；2.上海海事大学 商船学院，上海 201306)

管接头在飞机液压系统中起管路连接作用，其密封性能与可靠性对管路安全至关重要。目前，我国航空液压管接头主要采用可分离的74度锥和球形密封结构，实践表明，现役管接头在液压系统管内压力为22 MPa时多次出现泄漏问题，给飞行安全带来隐患，管接头的密封可靠性亟需提高[1-2]。梁式管接头于20世纪80年代在美国兴起，与锥面管接头和球面管接头相比，梁式管接头具有安装间距短、自紧性和自封性的特点，适用于压力为20.7～55.2 MPa的液压系统，有望成为我国航空耐高压管接头的替代型式[3]。SAE标准指出，梁式管接头由阴接头、阳接头与外套螺母组成，其主要密封结构为阴接头的U型截面与密封梁[4-5]。梁式管接头在装配时可形成两道有效密封，第一道密封为主要密封结构，第二道密封的作用为防止振动或弯曲载荷传递到第一道密封，保证密封的稳定可靠。SAE标准对阳接头给出结构形式和尺寸，阴接头需由研究人员自行设计[6]。目前，国内外对梁式管接头设计与性能研究鲜有公开发表的文献。Jeon等[7]和李晓东[8]将梁式管接头的阴接头设计为双锥度结构，数值模拟表明该结构仅能形成一道具有较大接触应力的密封。崔颖等[9]设计了一种带有椭圆弧凹槽的阴接头结构，有限元仿真表明该型梁式管接头在装配过程中可形成两道有效密封，并通过试验验证了理论分析的准确性。一直以来，静密封性能主要由接触应力或接触带宽的大小来判断，缺少统一的定量标准。Cui等[10]提出了综合考虑梁式管接头密封面接触带宽与接触应力的密封性能S指数定量评价指标，并得到了影响密封性能的主要结构敏感参数。当前国内对梁式管接头的研究处于初始阶段，尚有大量问题有待深入研究。

与不锈钢相比，钛合金具有质量轻、强度高的特点，能够满足航空管接头对质量和高密封可靠性的需求。在现有研究成果的基础上，有必要开展钛合金梁式管接头结构优化设计研究。近年来，一些学者对多种类型管接头开展优化研究，使密封性能得到一定程度的提升[11-14]。这些研究工作大多利用实验设计方法对管接头进行优化，由于实验设计方法取值空间较小，数据量较少，有必要采用更高效的优化方法对梁式管接头进行结构优化。

Isight软件提供了多种优化算法，具有强大的优化设计功能，其中多岛遗传算法有较好的全局优化能力，并且优化效率较高[15]。本文在钛合金梁式管接头接触力学有限元建模和敏感参数分析基础上，确定了设计参数的合理选取范围，数值模拟得到大范围参数空间内管接头结构的接触应力、接触带宽和S密封性能指数的样本空间。基于Isight软件，利用神经网络模型建立代理函数，以S指数为优化目标函数，运用多岛遗传算法进行全局优化，得到最优结构设计参数，从而为航空钛合金梁式管接头的结构优化提供了方法和设计依据。

1 钛合金梁式管接头有限元仿真分析

首先对图1所示的带有椭圆弧凹槽的梁式管接头结构进行参数化设计。阴接头参数化后截面形状与结构参数如图2所示[10]。

针对管径规格为Φ12 mm的梁式管接头，利用有限元法建立弹塑性接触模型并进行仿真分析，结构参数取值如表1所示。

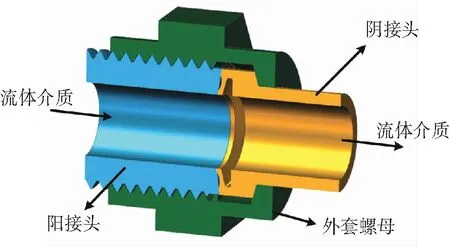
图1 梁式管接头结构示意图Fig.1 Schematic diagram of beam seal

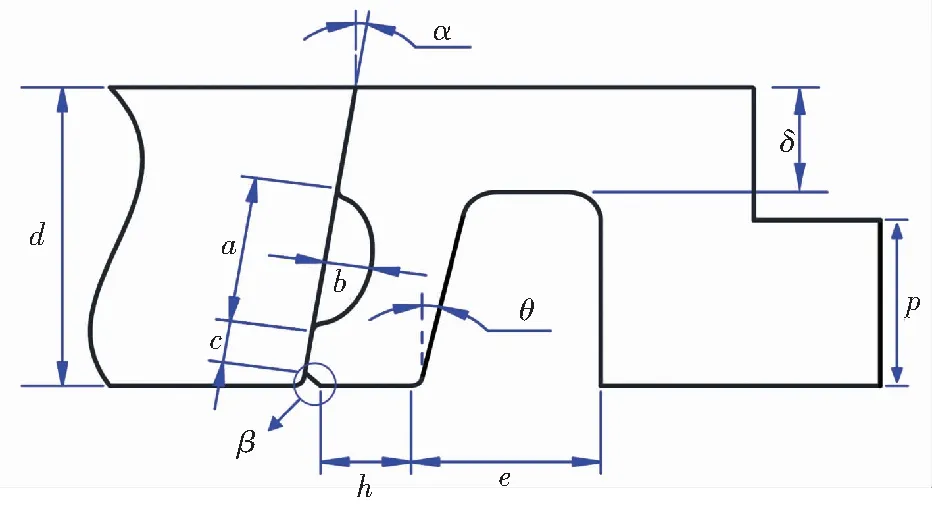
a—U型梁椭圆弧凹槽长轴；b—U型梁椭圆弧凹槽短轴；c—第一道密封名义接触带宽;d—阳接头壁厚；e—U形口轴向长度；h—密封梁截面宽度；p—阴接头壁厚；α—锥面角；θ—U型梁与径向夹角；β—倒角角度；δ—U型梁底部与阴接头外径的距离图2 梁式管接头结构参数化Fig.2 Parameterization of beam seal

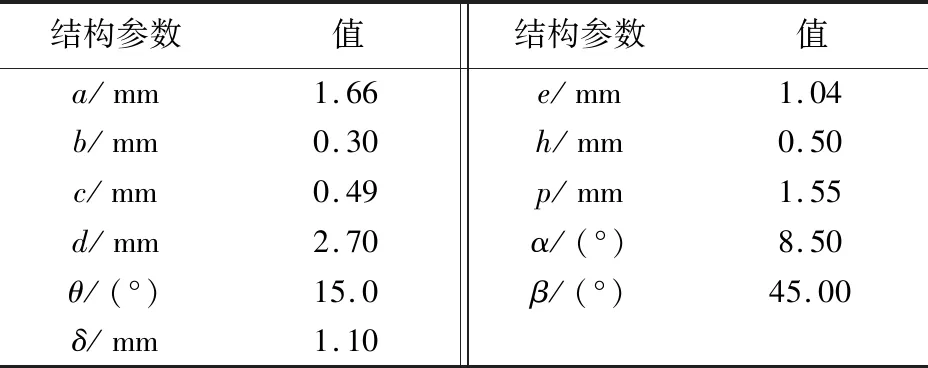
表1 梁式管接头结构参数Tab.1 Parameters of beam seal

阴阳接头材料为钛合金，弹性模量E=109 GPa，泊松比μ=0.34，塑性本构关系如表2所示。

表2 TC4钛合金塑性参数Tab.2 Plasticity parameters of TC4 titanium alloy

将阴接头接触面设为主面，阳接头接触面设为从面，接触面摩擦因数为钛合金-钛合金接触无润滑条件下典型取值0.15[16]。应用有限滑移和表面与表面接触对接触面进行约束。在阴接头外套螺母位置创建参考点RP-1，建立RP-1与阴接头受力区域之间的连续分布耦合约束来模拟外套螺母与阴、阳接头的连接关系。根据实际受力情况，在阳接头底部施加固定约束，在RP-1耦合点处施加轴向预紧力载荷，如图3所示。

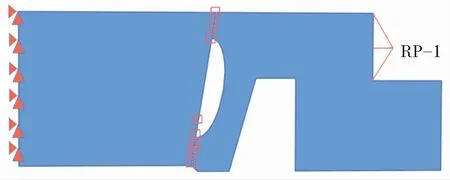
图3 有限元计算接触设置Fig.3 Contact settings for finite element calculation

有限元网格采用二次轴对称四边形单元CAX8R，为防止主从面发生穿透，对阳接头网格进行加密。由于梁式管接头为轴对称模型，计算速度较快，因此在设置网格时均采用小尺寸网格以保证计算精度。设置阴接头第一道密封面网格尺寸为0.008 mm，阳接头网格尺寸为0.006 mm；阴接头第二道密封面网格尺寸为0.030 mm，阳接头尺寸为0.020 mm。总计网格17 456个，如图4所示。

图4 网格划分Fig.4 Grid division

根据SAE标准，管径Φ12 mm的梁式管接头的拧紧力矩范围49～54 N·m[17]，由螺母扭拉关系确定预紧力的范围为14 700～19 000 N[18]。在预紧力为17 000 N条件下采用Newton-Raphson法与对称罚函数法计算接触应力，得到两道密封的接触应力分布云图如图5所示。

图5 密封面接触应力分布Fig.5 Contact stress distribution on sealing surfaces

由5图可知，带有椭圆弧凹槽的梁式管接头可在密封面上形成两道有效密封，第一道位于管路内径处，第二道位于管路外径处。第一道密封接触带宽狭窄，为线密封，第二道密封接触带较宽，为面密封。同时，定义第一道密封的径向路径并提取路径上节点的接触应力值，得到沿阳接头锥面母线第一道密封接触应力的分布规律，如图6所示。接触应力在第一道密封面上非均匀分布，在0～0.08 mm范围内，接触应力为0 MPa；在0.08～0.13 mm时，接触应力逐渐增大，最后降低为730 MPa。梁式管接头在装配过程中，第一道密封在内径端部发生翘曲，导致第一道密封内径处接触应力为0，真实接触带宽小于名义接触带宽。翘曲产生的原因为第二道密封为固支端，第一道密封为滑动支撑的简支梁，随着预紧力的增大，密封梁发生变形，第一道密封滑动，同时第一道密封接触合力为密封梁提供向上的支持力，在第一道密封接触合力的作用下，密封梁内径端部发生翘曲。

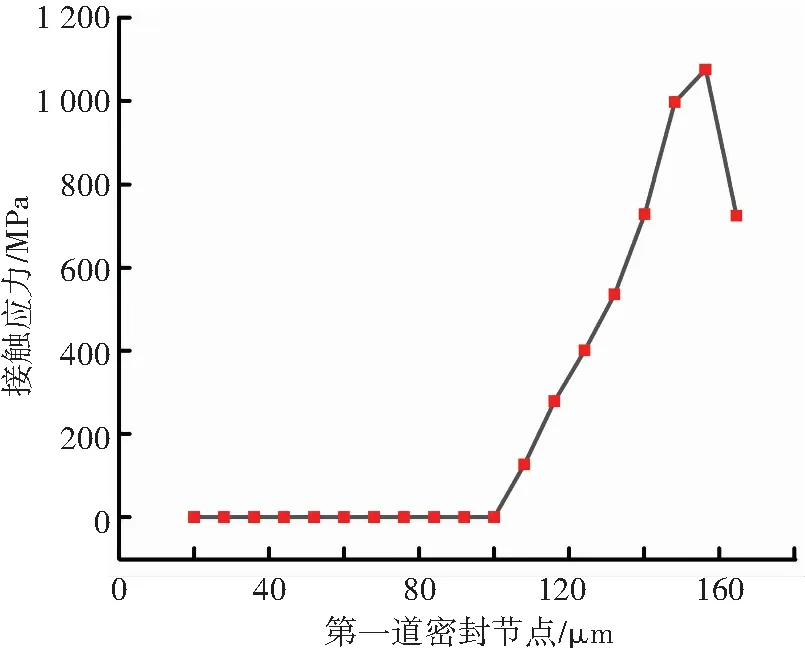
图6 第一道密封接触应力分布Fig.6 Contact stress distribution on the first sealing surface

梁式管接头的有限元模型已在文献[9]中通过实验验证了其有效性。实验原理如图7、8所示。

图7 实验装置与试验件Fig.7 Experimental rig and test piece

图8 压敏测试胶片放置图Fig.8 Diagram of pressure sensitive test film placement

试验由阳接头固定件、加力件、压力传感器、阳接头、阴接头、垫片与液压缸组成。加力件与阴接头配合模拟外套螺母对梁式管接头施加预紧力，阴接头、阳接头与加力件配合构成试验主体。为准确测量密封面上接触应力分布与接触带宽，将高精度FUJI压敏测试胶片放置于阴阳接头接触配合面。垫片与加力件之间安装压力传感器，用于测量施加于梁式管接头的预紧力。加载后的梁式管接头接触带宽如图9所示。

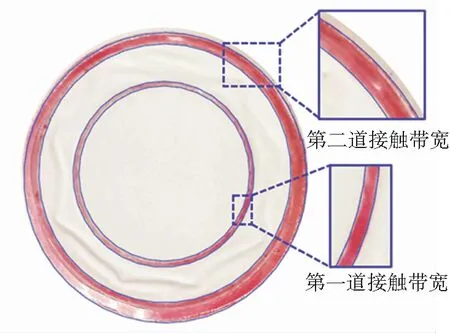
图9 梁式管接头两道密封Fig.9 Two seals for beam seal

由图9可知，梁式管接头在装配过程中可形成两道有效密封，第一道位于内径处，第二道位于外径处，实验结果与有限元计算结果一致。将不同预紧力下两道密封的接触带测量结果与有限元计算结果进行对比，见图10。

由图10可知，试验结果与有限元模拟结果趋势相同，试验得到两道密封的接触带宽均高于数值模拟结果，这与压敏胶片在受到较大压力时会有少量颜料渗出有关，试验结果与计算结果平均误差为20%，数据吻合较好，验证了本文所采用的接触有限元分析方法的有效性。

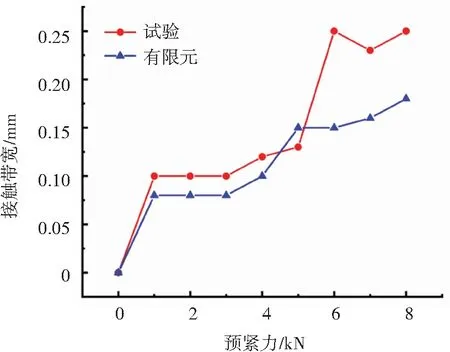
(a)第一道密封接触带宽对比

2 密封性能评价指标

Perrson等[19]研究指出，金属静密封发生流体泄漏的根本原因在于粗糙接触界面上存在贯通的微观通道。Perrson应用二维逾渗栅格模型描述接触后的密封区域，逾渗栅格模型如图11所示。图中黑色网格代表接触区，白色网格代表非接触区，黑色网格数量与总网格数量之比为接触面积比φ。对黑白网格的数量进行控制，逐渐增加黑色网格的数量，即增加接触面积比，应用自编的寻径算法寻找是否存在贯穿栅格模型的通路，若存在通路，则发生泄漏[20]。采用寻径算法对不同接触面积比的栅格模型进行600次的循环计算，得到泄漏概率与接触面积比的关系曲线，如图12所示。

由图12可知，当接触面积比达到0.4时泄漏概率发生陡降；接触面积比为0.43时泄漏概率为0；临界接触面积比是一个统计的临界量，与粗糙面的表面形貌无关。根据以上分析，将对应于接触面积比为0.43时的名义接触应力定义为临界接触应力pc。为得到对应于粗糙度为0.4密封面的临界接触应力，本文采用文献[21]中经试验验证的粗糙面接触力学仿真方法，建立钛合金双粗糙面接触有限元模型，如图13所示，材料参数如表2所示。

(a)φ=0.4

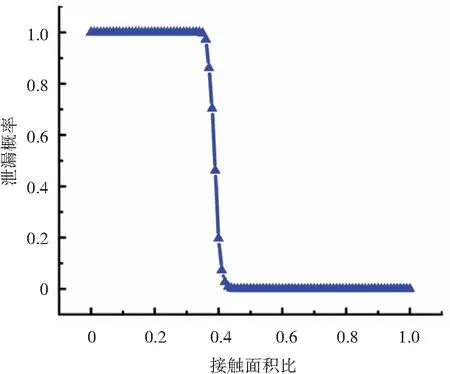
图12 泄漏概率与接触面积比关系曲线Fig.12 Relation between contact area ratio and leakage probability

图13 双粗糙面接触模型Fig.13 Contact model of double rough surfaces

为提高计算效率，将粗糙面分为基底层与粗糙面层。基底层采用10节点四面体单位C3D10M，粗糙面层采用六面体非协调单元C3D8I，划分网格242 122个。对下粗糙面底面施加固定约束。为使有限元模型在计算过程中易于收敛，采用位移载荷代替力载荷，对上粗糙面施加向下的位移。计算得到钛合金材料接触面积比与接触应力的关系曲线如图14所示。由图14可知，粗糙度为0.4的钛合金密封界面临界接触应力pc为890 MPa,即密封面上只有大于临界接触应力pc的区域可形成有效密封。

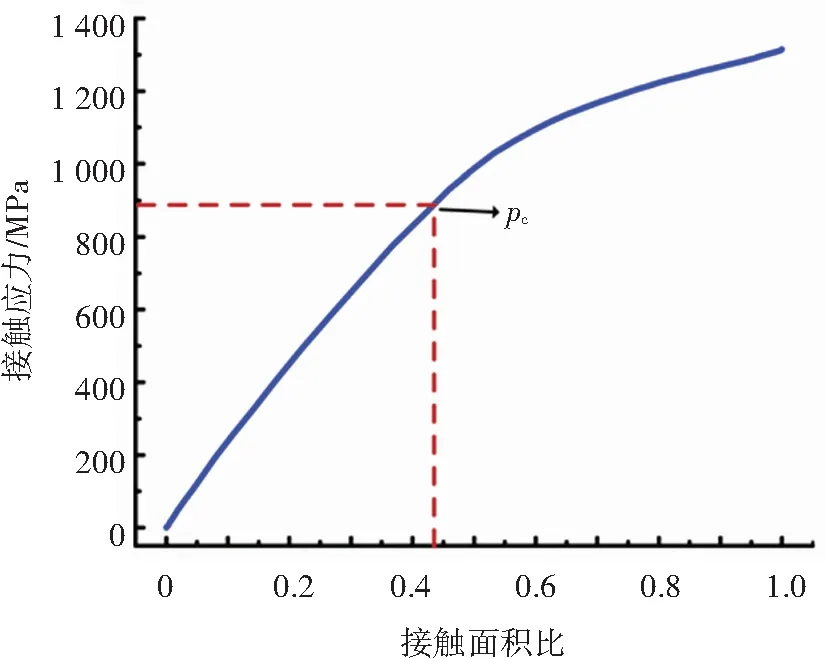
图14 接触面积比与接触应力关系曲线Fig.14 Relation between contact area ratio and contact stress

根据以上分析，为量化有效密封区域，文献[9]综合考虑梁式管接头宏观结构与接触面微观形貌，提出了综合考虑接触带宽与接触应力的S指数密封评价指标：

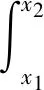
(1)

式中：f(x)为密封面接触应力分布函数，x1与x2为f(x)与pc交点的横坐标。积分原理图如图15所示，S指数越大，密封的可靠性越高。因而，本文将S指数作为评价钛合金梁式管接头密封性能的指标。

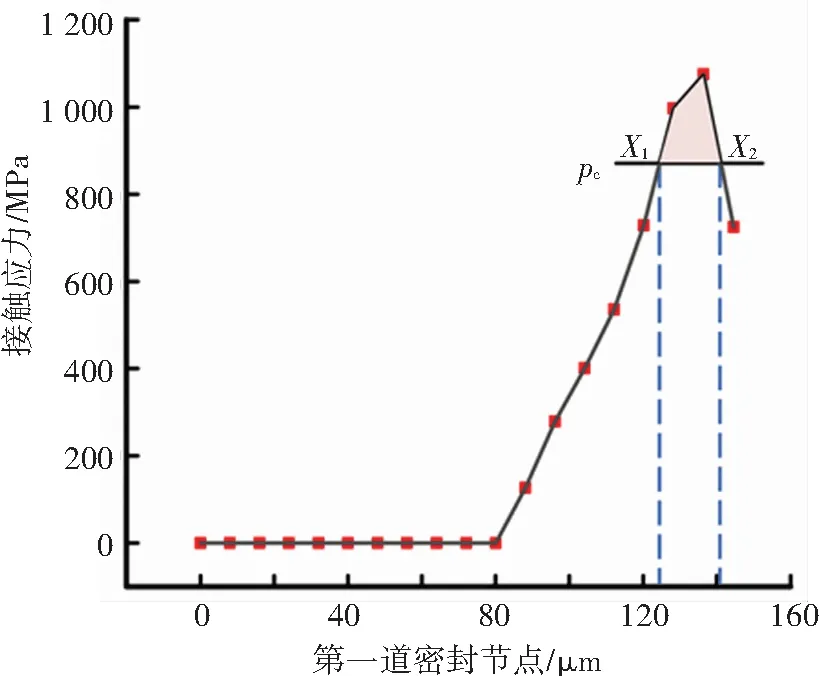
图15 S指数积分示意图Fig.15 Schematic diagram of S index integral

3 结构优化方法与流程

选取对密封性能敏感的结构参数为设计变量，以S指数为目标函数，利用Isight软件对钛合金梁式管接头的结构进行优化设计。在文献[10]梁式管接头敏感性分析的基础上，选取表3中5个结构参数作为优化设计变量，并根据结构尺寸选取敏感结构参数合适的变化范围。

表3 优化设计变量的取值范围Tab.3 Values of optimization design parameters

利用ABAQUS软件的Python脚本功能，将梁式管接头有限元建模与计算过程进行参数化，使设计变量在表3中设定的取值范围内遵循均匀分布取值的原则，得到各组管接头结构参数下的接触应力与接触带宽。基于得到的接触应力分布曲线数据库，对数据库中接触应力超过钛合金材料临界接触应力(pc为890 MPa)的有效密封区域进行积分，得到240组数据的S指数数据库。

将S指数数据库导入神经网络模型,得到管接头结构参数变量与S指数之间的拟合函数，基于该拟合函数采用Optimization模块中多岛遗传优化算法(MIGA)进行优化，并判断得到的性能最优阴接头几何构型是否符合要求，如果不符合要求则需再次优化，直到符合要求为止。阴接头结构优化的流程如图16所示。

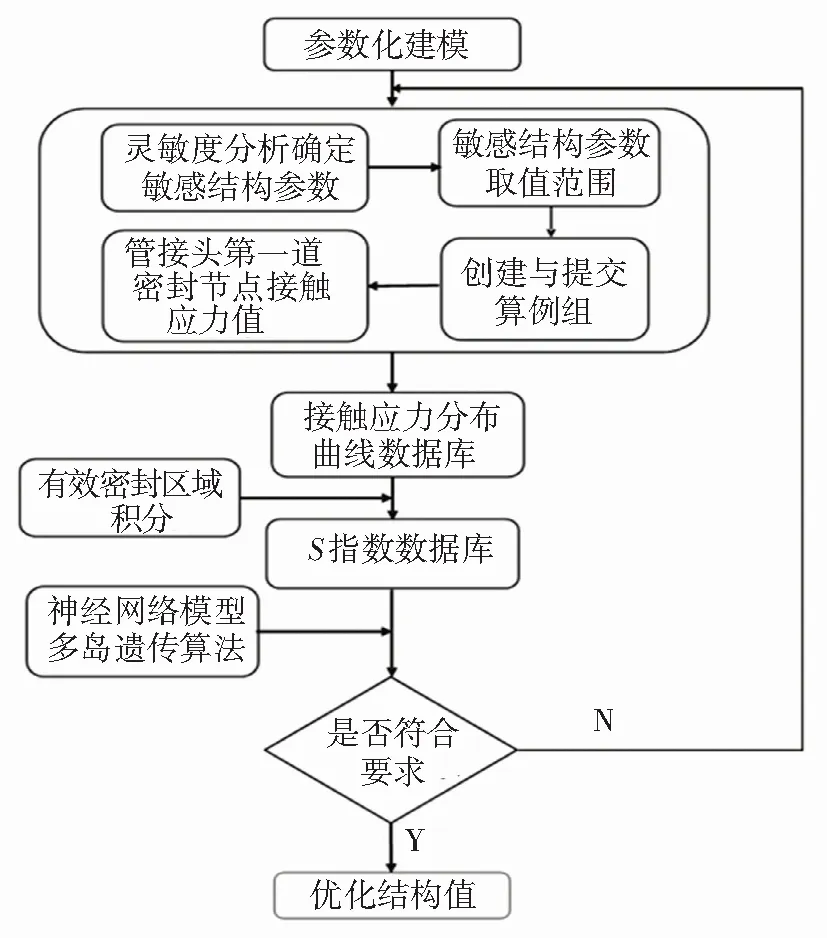
图16 结构优化流程图Fig.16 Flow chart of structural optimization

4 优化结果与验证

基于上述优化流程，得到阴接头最优几何构型。原型结构、数据库S指数最大值结构(极值结构)与优化结构的几何参数与S指数对比如表4所示。

表4 优化前后对比Tab.4 Comparison before and after optimization

表4中优化结构所对应的S指数为基于数据库采用优化算法预测的结果，有必要对该最优结构采用有限元建模计算验证。采用前述的有限元方法计算得到最优结构的S指数为3.66 MPa·mm。优化值3.92 MPa·mm，相对偏差为7.1%，表明优化结果具有较高的准确性。优化结构的S指数比原型的S指数提高102.2%，比数据库最大值结构的S指数提高53.1%，优化结构的密封性能得到了显著提高。

有限元计算得到的以上3种结构的第一道密封接触应力分布如图17所示，由图17可知，相比于极值结构与原型结构，优化结构第一道密封接触带宽上的接触应力有明显提高，实际接触带宽增大。

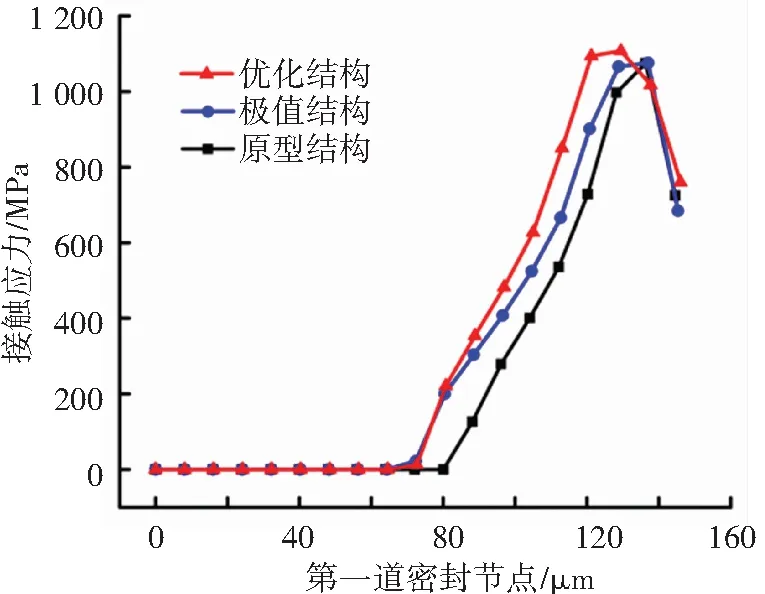
图17 接触应力分布对比图Fig.17 Comparison of contact stress distribution

5 结 论

1)提出了航空梁式管接头结构优化设计分析方法。基于ABAQUS软件建立钛合金梁式管接头有限元接触分析模型，能够得到梁式管接头两道密封的接触应力与接触带宽。利用第一道主密封的S指数密封性能指标，应用Isight软件和多岛遗传算法进行优化，可得到密封性能最优的结构参数。

2)针对钛合金航空梁式管接头密封性能评价标准，通过钛合金微观粗糙表面的有限元接触分析得到给定粗糙度下临界接触应力，结合宏观有限元得到的接触应力分布计算S指数。S指数的评价指标比传统单纯以接触应力或者接触带宽评价密封性能的方法更加完善，可作为结构优化设计中量化的密封性能目标函数。

3)本文对管径为12 mm的梁式管接头结构的优化结果进行了有限元计算验证，两者偏差为7.1%，表明优化方法具有较高的准确性。优化结构第一道接触密封上接触应力与接触带宽比原型结构明显增大，S指数提高102.2%，表明优化结构的密封性能显著提升，从而为提高钛合金梁式管密封性能的结构参数优化设计提供了理论方法，同时也可对其他工程结构优化设计提供参考。