费马原理之巧思应用

张思宇

(东北师范大学物理学院 吉林 长春 130024；山西大学附属中学 山西 太原 030006 )

王伟

(东北师范大学物理学院 吉林 长春 130024)

物理教学以培养学生物理学科核心素养为重，物理学认识路径是物理学科本质的集中体现，随着研究的深入，需进一步加深认识路径由简单到复杂的思维层级，为学生物理学科能力发展提供可视化依据.加深理解和掌握认识路径，离不开在真实情境中解决具体问题的过程[1].

费马原理，在中学、大学阶段都有学习，本文将费马原理应用于中学物理，求解所需时间最短路径等实际问题.到大学阶段，为进一步加深理解费马原理，运用其推导出厚透镜、柱形透镜物像方程，并通过居家实验探究其成像规律，以助于培养学生的科学探究能力.

1 理论基础

费马原理可以表述为：光在空间中从一点传播到另一点，实际的光程总是一个极值.也就是说，光传播的实际路径，其光程为极小值、极大值或恒定值[2].在一般情况下，实际光程大多数是取极小值，但光程为极大值及恒定值的情况也存在.

2 应用费马原理巧解最短时间问题

在求解中学物理问题时，遇到求解匀速运动的最短时间路径题，可以将运动路径与光的传播路径类比，根据求解问题的类型，选择使用折射定律或者反射定律的结论，去进行求解[3]，这样可以避免使用导数求解，从而使问题简化.求解这类问题可以应用费马原理，将物体运动的速度看作光在不同介质中的速度，物体运动的路径看作光的传播路径.

以一具体实例来论证.如图1所示.当海里有人溺水时，岸上的人要进行施救，人在陆地中的速度为vr，在海里的速度为vs，施救者到海岸线的垂直距离为d1，溺水者到海岸线的垂直距离为d2，两者与海岸线垂足之间的距离为h，那沿着怎样的路径人可以最快到达溺水者位置进行施救？

解：运用费马原理求解，施救者路径即为光的传播路径，从施救者到达溺水者的位置，看作光从一种介质到另一种介质，发生了折射，满足光的折射定律

n1sinθ1=n2sinθ2

(1)

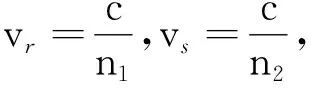
vssinθ1=vrsinθ2

(2)

(3)

求解式(3)，得到x的值，从而求得最优路径.依据费马原理可得，在一般情况下，光会沿着所需时间最短的路径传播，求得最优路径，即求解所需时间最短的路径为光的实际传播路径[4].

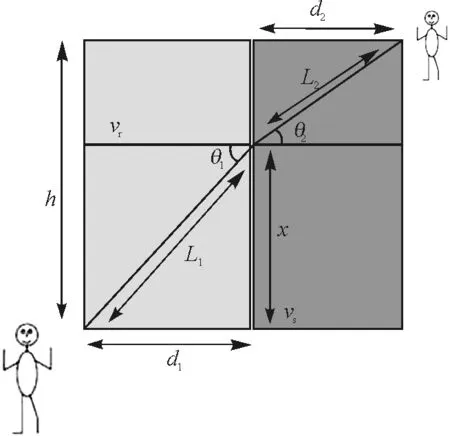
图1 最短时间问题示意图

3 柱形透镜

费马原理的思想贯穿在整个物理学习过程中.在大学学习阶段，随着几何光学学习的深入，对于一些复杂的光学元件大多采用逐次成像法得到其物像方程[2]，对费马原理的应用开始减少.本文直接运用费马原理，采用极限思想，推导出主轴外物点，在非近轴光线条件下厚透镜物像方程.从本质上解释近轴近似的原因，并具体应用到实践中.

新搬来的那个女人很漂亮，约莫二十岁出头，高挑的个头，瓷白的皮肤。每天傍晚的时候，她都喜欢穿着一条曵地的白色纱裙，像例行公事似的在院子里打理一小会儿花草，然后就回到那间亮着橙黄色灯光的屋子里弹钢琴。女人喜欢弹奏贝多芬的《致爱丽丝》和法国保罗·赛内维尔和奥立佛·图森共同谱写的那首《秋日思语》。一般情况下，女人在弹奏曲子的时候，我都会关掉灯，放下手里的事情，和大黑猫一起默不作声地伫立在窗前往对面的屋子里打量。

3.1 厚透镜物像方程

光线经厚透镜折射光路如图2所示.

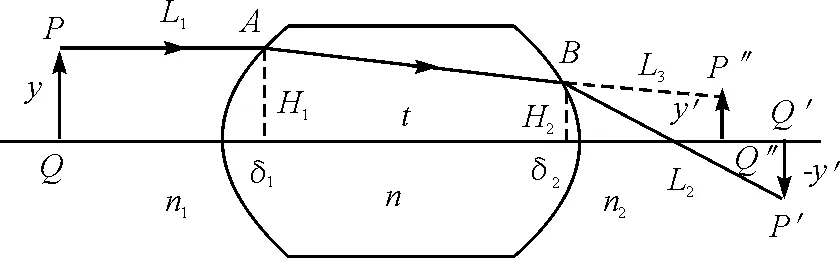
图2 (主轴外物点)厚透镜折射光路图

由P点发出的光线经厚透镜两次折射后成像于P′点，图中P″点为光线经过第一个面折射后的中间像，其中AP″=L，厚透镜第一个折射面的曲率半径为R1，第二个折射面的曲率半径为-R2，则光程为

ΔPABP′=n1L1+nL-nL3+n2L2

(4)

改变入射光线，H1,H2随之而变.由费马原理可知，光程应为极值或恒定值，采用极限思想，将光程对H1,H2求导均为零

(5)

(6)

由于H1是变量，等式成立条件为两边系数均为零，可得式(7)，同理,光程对H2求导，可得式(8)，推导得到主轴外物点、在非近轴光线条件下厚透镜物像方程式(7)、(8)

(7)

(8)

在近轴近似条件下，H1,H2,y,-y′,δ1,δ2均为小量，进一步可得出近轴光线条件下厚透镜物像方程式(9)、(10)

(9)

(10)

本文通过推导过程说明近轴近似的原因，推导过程简单明了，没有使用太多的数学技巧，适合刚进入大学的学生学习[5～7].

3.2 柱形透镜物像方程

随着研究的深入，需进一步加深认识路径由简单到复杂的思维层级，在真实情境中解决具体问题.本节应用费马原理，进一步深入研究柱形透镜物像方程，并通过实验探究其成像规律，为学生物理学科能力发展提供可视化依据[1].

如图3所示，柱形透镜在竖直面内为一个矩形，光线通过并不会产生偏折，在水平面内的截面为一个圆形透镜，可看作为一个特殊的厚透镜[8]，厚透镜的厚度为t=2R.

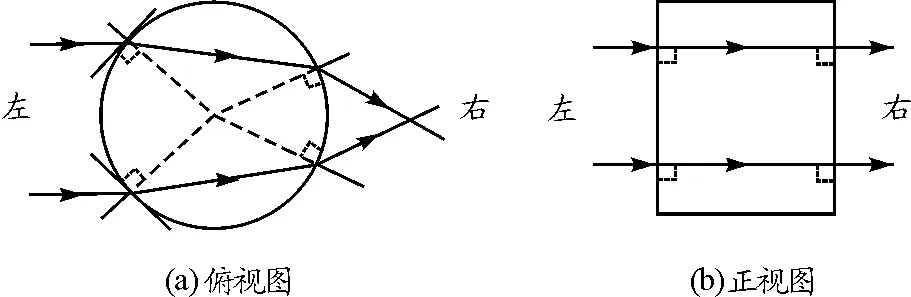
图3 柱形透镜俯视及正视图

R1=R为厚透镜第一个折射面的曲率半径，R2=-R为第二个折射面的曲率半径，将其代入式(9) 和 (10) ，可得在近轴近似条件下，柱形透镜水平面内物像方程

(11)

当光线平行入射(或出射)，即s→-∞,s′→∞时，可分别得出像方(或物方)焦距

(12)

(13)

将柱形透镜放置在空气中，即n1=n2=1时

(14)

近似简化令物点到厚透镜前表面的距离为物距，厚透镜后表面到像点的距离为像距，所以式(14) 得出的焦距为像点到柱形透镜后表面的距离.

4 居家实验探究

通过居家实验探究柱形透镜成像规律.

实验器材：柱形塑料杯(直径6.2 cm，高度14.0 cm)，溶液(水、饱和食盐水)，带有左右部分反写的“光学”字样纸板.

注意：将纸板上的图案、柱形水杯的几何中心，及观察者视线位于同一直线上，并且尽量使图案小一点(尽量满足近轴物在近轴光线条件).

如图4和图5所示，通过装满溶液的圆柱形杯，去观察纸片上的文字；改变纸片与柱形水杯的距离，观察各种成像特点，从而得到圆柱形透镜的成像规律，并与理论值对比.在玻璃杯中注入水或饱和食盐水，使液体高度超过图案即可；通过观察可以发现，像在水平面内发生变化，左右颠倒，图案变宽，而在竖直平面内没有发生变化[9].

图4 加水前的成像

图5 加水后的成像

由式(14)可得装满水的柱形透镜(水的折射率为1.33)，其焦距为f=3.10 cm；装满饱和食盐水的柱形透镜(盐水折射率在1.38左右)，其焦距为2.53 cm左右；改变纸片到柱形玻璃杯壁距离，观察到的成像情况如表1所示.

表1 柱形透镜成像规律

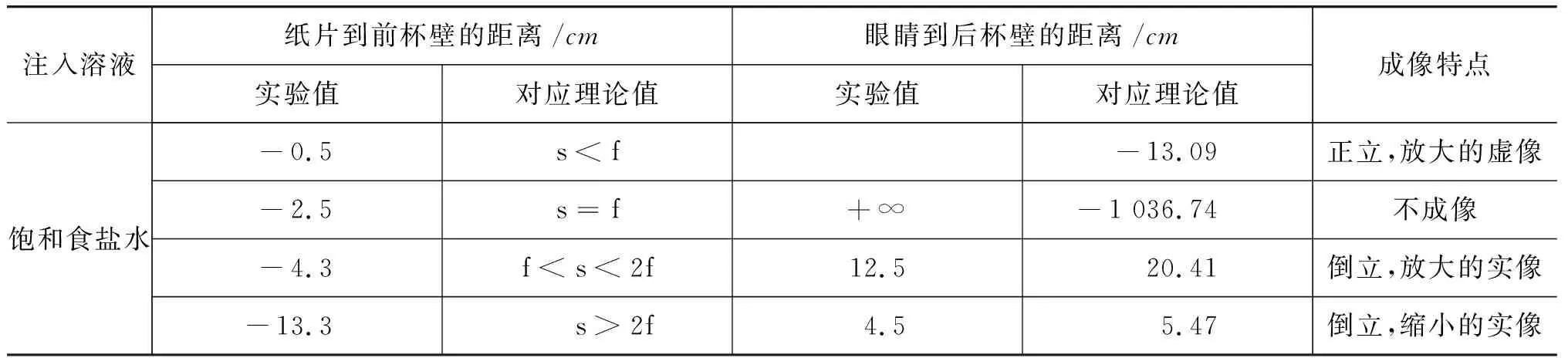
续表1

通过实验与计算得到的理论值进行对比，对于不同位置的成像特点与理论所对应的范围一致，但对于成像位置有较大的误差(在实验中为了减小误差运用了杯壁较薄的塑料杯)、像差等原因导致很难选出最优的图像，所以得到的物距与理论值差距较大.

5 结束语

通过对物理规律的学习，运用科学探究的方法去研究问题，并将其具体应用到实际生活中，有助于促进学生科学探究能力的发展.

费马原理作为几何光学的基本理论，不论对中学生还是大学生，对理解几何光学的物理本质有着非常重要的作用.本文旨在从本质上进一步探讨和说明，费马原理在几何光学学习中的重要性，将其应用到厚透镜物像方程的理论推导，并在居家实验中亲自研究验证，以助于学生更深刻地理解其思想，为后续学习打下扎实的基础.