无叶扩压器半径比对交叉扩压器影响的研究

吕文，宋丹路，汪林生，张津晨

(1.西南科技大学 制造过程测试技术教育部重点实验室，绵阳 621010；2.西南科技大学 制造科学与工程学院，绵阳 621010)

0 引言

斜流压气机具有单级增压比高、结构简单、稳定裕度大等优点，其应用越来越广泛[1～3]，长期以来一直是国内外学者密切研究的热点[4,5]，受到愈来愈多的重视。但是斜流压气机必须要有匹配的扩压器才能工作，而扩压器设计的好坏对斜流压气机性能有重要影响[6～9]。合适的无叶扩压器匹配斜流压气机之后，不仅能提升斜流压气机运行稳定性，而且能够提高叶片扩压器的性能，最终影响整机的效率。Shum等人[10]研究了无叶片间隙的变化对压气机性能的影响。研究表明，无叶扩压段对压气机的级性能有显著影响。Aungier指出[11]，无叶扩压器可以使气流在进入扩压器之前适应扩压器叶型。因此可以帮助减小叶轮出口处的混乱尾流，从而提升性能。无叶扩压器影响整机效率的主要因素体现在尺寸上。叶轮和扩压器之间无叶扩压器长度的增加会导致叶片扩压器前缘的马赫数减少，可提升叶片扩压器性能。

在大多数文献中，无叶扩压段被量化为叶轮出口半径和叶片扩压器进口半径之间的半径比值L(L=r3/r2)。但是，无叶扩压段半径比这个值并不是固定的，而且许多其他引用对于无叶扩压段的大小有不同的标准。Ziegler等人[12]研究了叶轮和扩压器之间的实验流动相互作用。它们的半径比在1.04到1.14之间（1.04≤L≤1.14）。研究发现，叶轮尾流随着半径比的增加而显著降低。他们还发现，较大半径比的无叶扩压器产生了较高的扩压器叶片进口总压力。Aungier[13]（2000）建议，半径比为1.06和1.12（1.06≤L≤1.12）。其中上值限制，可以尽量减少无叶扩压段的摩擦损失，因为较长的无叶段会导致更大的摩擦损失。下值1.06可以保证气体以平滑的方式进入扩压器扭曲的叶片之间。

目前，微型涡喷离心压气机的无叶扩压段长度范围是知道的，半径比在1.05～1.2之间。但是微型涡喷斜流压气机的无叶扩压器半径比的研究较少，没有探讨适应斜流情况下的半径比范围。因此本文以一款设计的斜流压气机和交叉扩压器作为研究对象，利用CFD数值模拟，开展斜流状况下无叶扩压器半径比范围的研究，并对不同子午面以及交叉扩压器内部流场加以分析。

1 研究模型与数值方法

本文研究对象为斜流压气机、无叶扩压器及其交叉扩压器。离心压气机无叶扩压段长度只需要保证径向方向就行，而斜流压气机由于出口角度小于90°，还需要考虑轴向方向的气体流动，比离心压气机情况更加复杂。为了考虑气流轴向位置运动，保证无叶扩压段方向沿着斜流压气机出口角度方向不变，以此简化气体流动。之后通过改变径向方向无叶扩压段半径比来得出斜流情况下的半径比值范围。

1.1 斜流压气机与交叉扩压器模型

本文利用某商用压气机设计软件的模块，选择真实气体为介质，具体结构参数如表1，之后再将一维设计的参数经过分析和修正，最终确定了斜流叶轮与扩压器的三维模型，如图1所示。交叉扩压器的优点是：当气流经过交叉扩压器时，由于扩压器通道是连续的，可以减轻因气流急剧转弯所造成的较大流动损失，这有助于提高交叉扩压器的扩压能力，有助于提升整级压比。

图1 斜流压气机与交叉扩压器三维模型

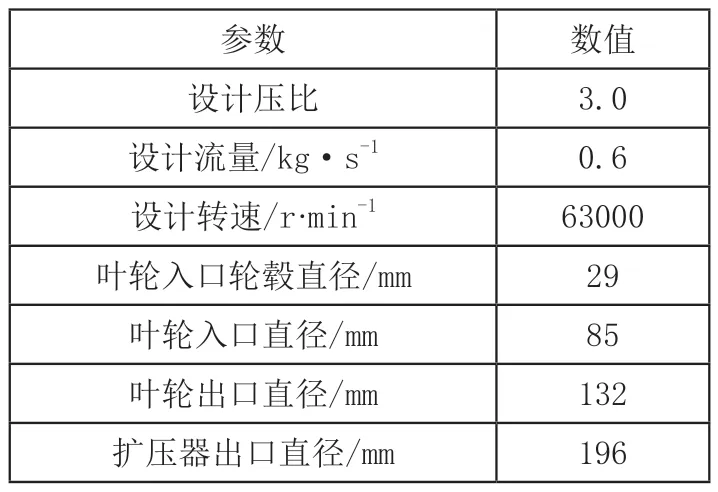
表1 斜流压气机与交叉扩压器参数

1.2 网格划分

网格划分是数值模拟的关键步骤，针对自行设计的斜流压气机与交叉扩压器，采用自动网格划分。网格应该越细越好，但是网格越细，计算的工作量就越大，计算的时间越久。综合考虑后，选取一个满足模拟要求的网格。网格如表2所示。斜流叶轮流道和交叉扩压器网格模型如图2所示。

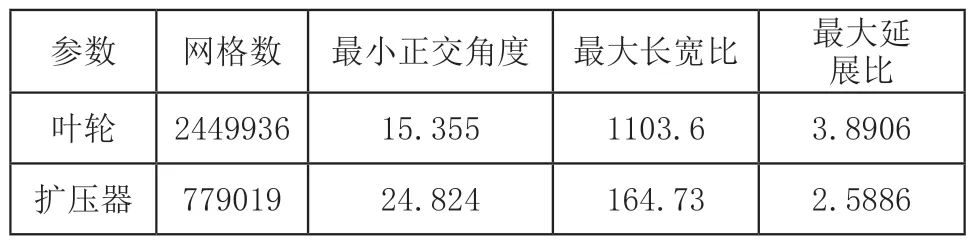
表2 叶轮与扩压器网格

图2 斜流压气机与扩压器叶轮网格细节

1.3 数值计算方法

边界条件：进口总压98000Pa，进口总温308K，给定出口质量流量。流体模型为真实气体，定常模拟。采用Spalart-Allmaras湍流模型和Turbulent Navier－Stokes方程组。表面设置为光滑、无滑移、绝热壁面，其中收敛系数为10^-6,最大迭代步数1500，CFL数为3，其他条件设置为系统默认值。

1.4 网格无关性验证

选取二百万到四百万网格之间的网格数进行稳态计算。对比分析等熵效率，可知：当网格数目达到一定值后，效率不再随网格数的增加而变化。即使不断加密网格，在网格数目增加了一百多万时，对整级的等熵效率和压比的影响都极小。网格数目对计算结果影响甚微。

2 计算结果分析

2.1 方案介绍

无叶扩压段是叶轮出口叶片和扩压器进口叶片之间的空间，如图3所示，R为扩压器半径，Z为子午面长度。该段的流动对叶片扩压器内流场特征会产生较大影响[14,15]，但目前该位置的研究仍然较少。在大多数文献中，无叶扩压段通常被量化为叶轮出口半径和扩压器叶片进口半径之间的半径比值L。

图3 网格无关验证

目前常用的离心压气机无叶扩压段半径比范围在1.05～1.12之间。相比于离心压气机，斜流压气机要考虑轴向位置，因此半径比应该大于离心时。本文选用离心压气机常用的半径比1.05、1.08、1.12进行排列组合，以此获得长度范围。共有6种方案进行分析，分别标记为方案A(1.05×1.05≈1.10）、方案B(1.05×1.08≈1.13）、方案C（1.08×1.08≈1.17）、方案D（1.05×1.12≈1.18）、方案E（1.08×1.12≈1.21）以及方案F（1.12×1.12≈1.25），各个方案中交叉扩压器叶片段和出口无叶扩压器段保持不变。通过对方案进行仿真分析后，从而得到斜流压气机无叶扩压段的半径比范围。

2.2 扩压段长度对扩压器性能的影响

斜流压气机整级性能特性曲线如图4、图5所示。分别是6种半径比方案中等熵效率随出口流量变化的曲线。

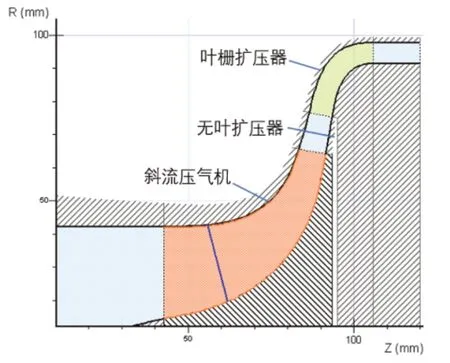
图4 子午面流道

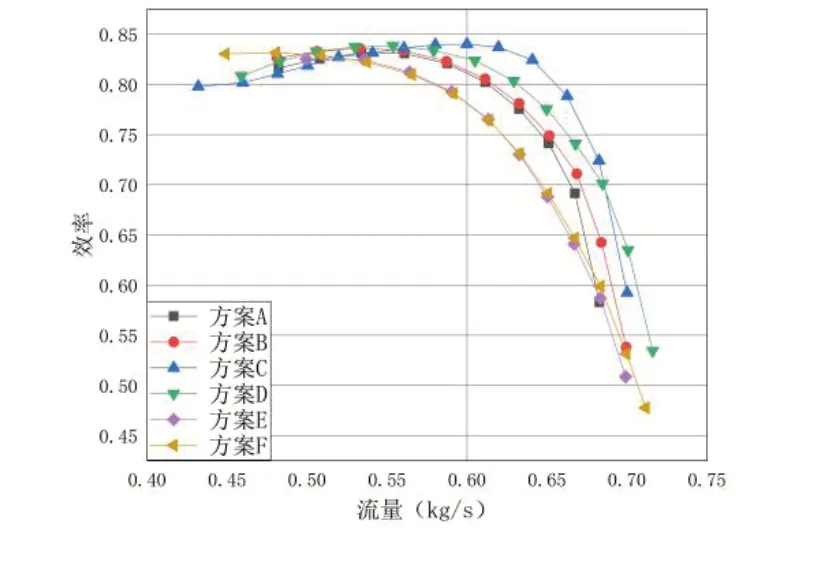
图5 效率-流量性能曲线

从图5可以看出，不同半径比的无叶扩压器对斜流压气机的效率有明显的影响。方案C的效率最高，方案E和F效率最差，可以说明随着无叶扩压段长度的增加，叶片扩压器性能先逐渐升高到达最高值之后再逐渐下降，气体流动随之恶化。

由图5、图6分析可知：一开始，随着无叶扩压器半径比的不断增大，等熵效率随着半径比增大而变大，压气机工作范围没有明显变化，压比变化没有效率变化明显，但变化趋势与效率特性曲线是一致的。而效率在方案E、方案F下降最为严重，且趋势一致，特性曲线几近重合。

图6 压比-流量性能曲线

3 流场分析

3.1 子午面压力分析

最终选取6个半径比工况下的设计点云图进行分析。以展现气体流动状况。图7给出了流量0.6kg/s时，不同半径比L下子午面的总压云图。观察图7，无叶扩压段的大小对斜流压气机出口处和交叉扩压器入口压力分布的影响是显而易见的。但是对斜流压气机入口压力的影响不明显。

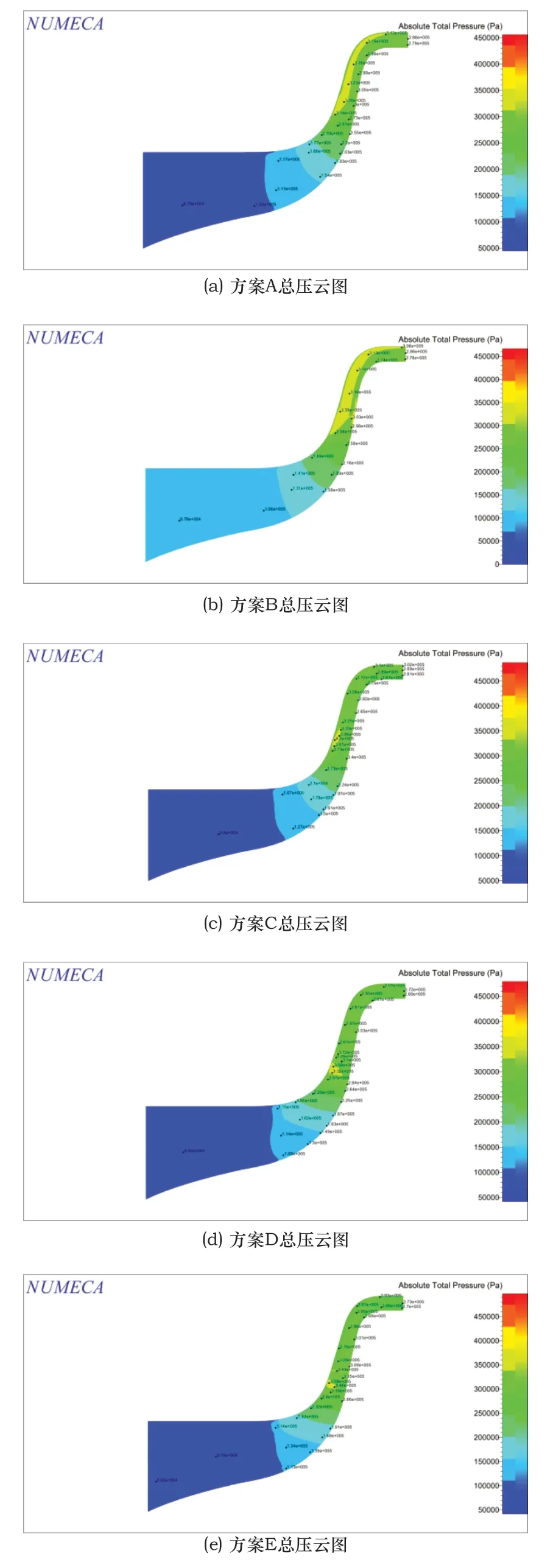
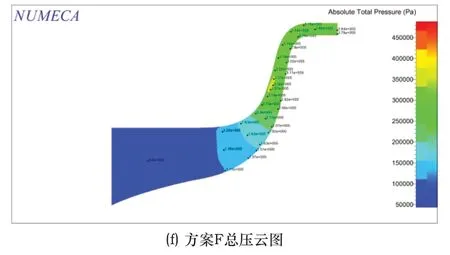
图7 6组方案的总压云图

在设计点流量0.6kg/s时，由图7方案A、B和C可知，无叶扩压器长度过短时，气体从无叶扩压器出口流出时，在无叶扩压器内部已经形成了高压流体，导致气流不仅在进入扩压器时产生损失还因为两段之间的高压区产生大量的能量损失，该高压流体区域甚至可以从无叶扩压段延伸到最终的气流出口处，影响最终的压比。这与扩压器出口回流区有关[16]。其主要原因是当L过小时，会造成无叶扩压器和有叶扩压器间的相互作用加剧，带来了一定流动损失，从而影响了压比。由图7方案D、E和F，随着无叶扩压器长度继续增大，交叉扩压器入口与无叶扩压器之间的高能流体区域逐渐变小，因此压比变大，如方案C高于方案A、B的情况。随着L的进一步加大，当无叶扩压段长度超过某个临界值时，无叶扩压段内的流动逐步变得均匀，高压区只在无叶扩压器内部产生且区域很小，不再扩散到交叉扩压器之间。但是由于无叶扩压器长度过长，导致与交叉扩压器气体混合处会气体掺混产生高压区。因而尽管方案E、F的气体流动情况相比方案A、B、C、D更好，但是无叶段与扩压器的过渡之间产生了更大的损失，导致压比反而更小。由上图5流量-压比特性曲线可知，压比会下降0.15左右。综合分析可知，无叶扩压器长度不能太小也不能太大，因此找出斜流情况下无叶扩压器半径比的范围非常重要。

3.2 扩压器（方案C）马赫数分析

图8给出了最高效率（半径比1.17）下交叉扩压器10%，50%，90%叶高处S1流面的相对马赫数云图。

观察图8可知，交叉扩压器气流进口相对马赫数为0.7左右，整个扩压器流场中激波造成的能量损失很小。但是整个交叉扩压器的气体掺混、尾流等现象比较严重，成为流动损失的主要原因。叶高从5%到50%时，交叉扩压器压力面的气流掺混区域减小，掺混的严重程度减小，由马赫数从0.2左右增加到0.38可知。吸力面处的尾流区域逐渐后移到叶片尾缘处，交叉扩压器出口的气体流动情况变好，相对马赫数由0.3增加到了0.38。再观察50%叶高和90%叶高处，尾流区域进一步后移到尾缘处，且区域范围大大减小，气体掺混的区域也收缩到叶片压力面处，因此扩压器出口的气体流动情况变得更好，马赫数再次变大。综上所述，随着叶高的增加，气体流动情况变好，尾流和气体掺混的区域与程度都不断减小。

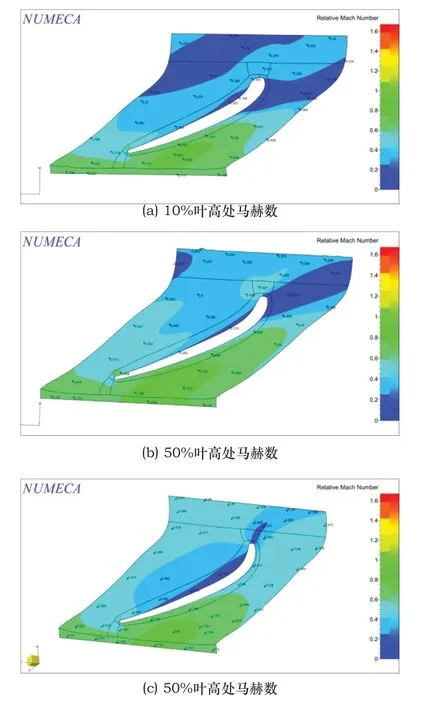
图8 方案C的总压云图

4 结语

对六组不同半径比的无叶扩压器进行了研究，得出如下结论：

无叶扩压器可以对斜流情况下的交叉扩压器产生显著影响，使整级性能曲线发生改变，效率在76.44%～84.01%之间变化。

半径比在1.10～1.17之间时，随着无叶扩压段长度的增加效率也增加至最大。效率之所以会明显提升，是因为无叶扩压器与有叶扩压器之间的流动状况得到改善。之后随着半径比从1.18～1.25，压比和效率反而下降，是因为气体掺混与气流急剧转折所造成的流动损失。

无叶扩压器对叶片扩压器的影响，不仅与径向长度有关，而且还与轴向尺寸有关系。因为长度增加，气体的流动距离变化，无叶扩压器与叶扩压器间的相互作用将加剧，通道间会形成高压流体区域。

斜流情况下的无叶扩压器半径比无量纲范围为1.10～1.25之间，相比离心时的范围1.05～1.12，范围区间变大，原因是气体的轴向方位流动。