基于模糊故障树的垂直升降式立体车库升降系统可靠性分析
王岳恒,马殷元
(兰州交通大学 机电工程学院,兰州 730070)
0 引言
垂直升降式立体车库以其占地面积小,存取效率高的优势,在城市繁华地段和人口密集场合应用越来越多[1]。升降系统是垂直升降式立体车库的重要组成部分,用于车辆在入口与存放点之间的垂直运载,往往会因为机械或电气故障,导致无法正常升降等故障,使立体车库无法正常运行。立体车库运行的安全可靠性不仅影响到车库的正常运行,还可能对车辆以及人员造成严重的安全威胁[2]。因此对升降系统可靠性进行分析十分有必要。
现有的故障树分析将事件发生概率视为一精确值,然而立体车库是一个复杂的机电系统,在实际应用中,很难确定事件发生故障概率的精确值。包括人为失误,一些故障发生频率较低导致无法获得大量的统计数据,系统建模不精确[3],这些原因都导致很难得到故障发生概率的精确值。
立体车库故障发生概率具有模糊性和不确定性,适合采用模糊数学理论来解决。本文以垂直升降式立体车库升降系统为例对系统进行可靠性分析,得出升降系统发生故障的顶事件和底事件的模糊故障率,克服了事件发生故障的不确定性,同时计算底事件的概率重要度并进行排序,为故障诊断顺序指明方向。
1 垂直升降式立体车库升降系统
1.1 垂直升降式立体车库工作原理
垂直升降式立体车库也称作塔式立体车库或者电梯式立体车库,优点在于整体占地面积小,单位面积可存放车辆多,因此主要用于城市繁华地段、高档小区、医院等车位需求量大且用地紧张的场景。
垂直升降式立体车库整体框架为钢结构,层数较高,两侧为停车位,中间为升降通道。车库主要由机械框架、升降装置、横移装置、控制系统等部分组成[4]。其中机械框架为整个车库停车的载体,升降装置的作用是将车辆提升或下降到目的层,横移装置的作用是将车辆泊入或泊出车位,控制系统是整个车库动作的核心,通过采集输入信息,分析处理后,输出提示或命令[5]。
1.2 升降系统
垂直升降式立体车库升降系统是整个系统运行的主要输送载体,在车库整体运行中起着非常重要的作用。垂直升降式立体车库,升降可以采用钢丝绳传动或链传动,升降平台也有多种。本文以常见的梳齿交换钢丝绳传动式为例进行分析,那么升降系统一般由升降电机、钢丝绳、升降台、电气系统组成,其中升降电机用于提供传输动力,钢丝绳是中间介质,升降台为车辆上下升降的载体,电气系统用于提供电信号与控制。
2 垂直升降式立体车库升降系统故障树的建立
故障树的建立是故障树分析中的重要一环。通过对以往的立体车库出现故障情况的整理,以升降系统故障为顶事件,以机械故障和电气故障为中间事件,进而深入分析出底事件,从而构建出合理的垂直升降式立体车库升降系统故障树模型。如表1为对导致升降系统故障的事件并进行了编码。图1为升降系统的故障树。

表1 升降系统故障事件编码表

图1 升降系统故障树
3 模糊故障树
3.1 模糊故障树概念
模糊数学理论最早是由美国专家Zadeh于1965年提出,其提出的背景是,在当时普通的集合无法描述元素模糊的归属问题,而模糊集合可以解释集合中的元素归属不明确问题,可以将元素的绝对隶属度相对化、模糊化,简而言之,可以将事件发生概率由精确值变为由概率区间化表示,即用模糊数来表示[6]。用模糊数来表示,可以更大程度的反应生产、生活中事件发生概率的不确定性,而不同条件下的概率值,可以用模糊隶属函数来表示,从而更加切合实际的反应出事件发生的概率,具有更强的适用性[7]。
模糊故障树就是将故障树分析法和模糊数学理论结合,将故障树对定值的分析推广到对不确定性的问题的解决,使得故障树分析法使用更加宽广。对模糊故障树进行分析时,先用故障树分析法进行故障诊断分析,再用模糊数计算得到模糊概率[8]。
这样在处理存在模糊性的故障时,工作人员就不用知道事件出现故障的精确概率值,降低了问题的处理难度,得到的结果和工程实践更加的接近,结果可靠度的也更高。
3.2 模糊概率表示
美国专家Zadeh给出了模糊集合的定义:
设在论域U给定了一个映射:

那么称A为U上的模糊集,UA为A的隶属度。
本文采用较为常用的三角模糊数来对故障树进行分析,三角模糊数A的隶属函数为[9]:

坐标图如图2所示:

图2 三角模糊数A的隶属函数坐标图
记A=(m,α,β),其中m为A的均值,α、β分别为A的置信上下限,α、β分布区间越大,则A越模糊,当α=0,β=0时,A有确定值,为非模糊数。假设λ(0≤λ≤1)为模糊数A的置信水平,则模糊数A可表示为区间数:

设有事件1、2,事件1、2的故障率为模糊数F1、F2,则有:

则事件1、事件2的与门和或门输出概率分别为:
1)与门结构

2)或门结构

通过式(2)和式(3)的与门与或门的计算公式,可以用于计算故障树模型中顶事件发生的概率。
3.3 模糊重要度
故障树分析的一个重要指标就是重要度,通过分析底事件发生故障的重要度,就可以分析出系统的薄弱环节,可以为系统改进指出明确方向。在计算时,有概率重要度、关键重要度等分析计算方法[10],本文采用概率重要度分析计算方法。概率重要度是基本事件发生与否,系统故障概率的减少量[11]。
设故障树分析中,设第i个底事件Xi的概率重要度表示为I(Xi),系统顶事件的故障概率表示为PT。Xi=1表示事件Xi发生故障,Xi=0表示事件Xi不发生故障。则底事件Xi的概率重要度可表示为:
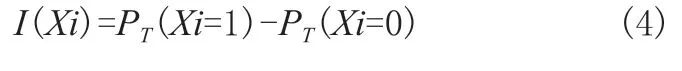
4 垂直升降式立体车库升降系统模糊故障树分析
4.1 顶事件故障概率
结合查阅的资料以及专家经验[12],分析得出升降系统故障树的基本故障率均值m和置信上下限α、β,如表2所示。

表2 各基本事件概率估计
假设各事件相互独立,则各事件逻辑关系式如下:
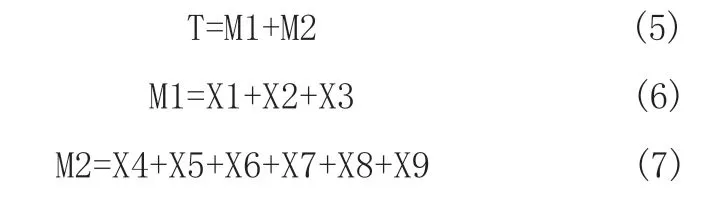
由以上可得:
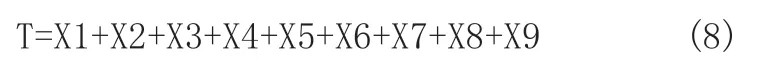
由式(1),对基本事件X1~X9作λ截集可得:


用截集λ表示的函数可表示系统顶事件发生概率[13],由式(3)、式(8)可得升降系统不能工作的概率FT可用截集λ表示为:

当λ=1时,FT=0.1023,即在不考虑各个基本事件所发生故障的模糊性时,升降系统无法正常工作的概率为10.23%;当λ=0时,其概率在[0.0763,0.1271]之间,表示在充分考虑了基本事件发生故障的模糊性时,升降系统不能正常工作的概率在7.63%到12.71%之间变化。该结果是一定量结果,为整个系统的故障分析提供了依据。
4.2 底事件重要度
根据概率重要度计算方法,由式(4)可得到各事件的概率重要度。中间事件的概率重要度为I(M1)=0.0194,I(M2)=0.083。因此中间事件对顶事件影响的排序为IM2>IM1。进而对中间事件M2进行分析。得出事件M2各底事件概率重要度如下表3所示。
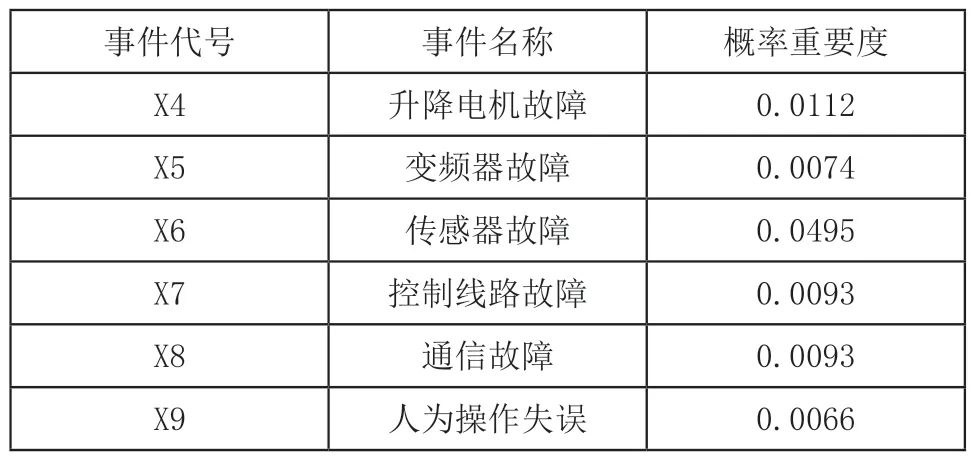
表3 事件M2各底事件的概率重要度
由表3可以得出事件M2各底事件的概率重要度排序为:I6>I4>I7=I8>I5>I9。由概率重要度分析可知,出现故障可能性最大的依次是传感器故障、升降电机故障、控制线路故障、通信故障等。如果出现故障,可按该顺序检查各零部件是否发生故障,可帮助维修人员快速查找故障。如果要提高升降系统的可靠性,可按上述顺序改进部件的可靠性,以改进系统。
5 结语
本文分析了垂直升降式立体车库的基本原理,并建立了升降系统的故障树,运用模糊数学理论,并结合历史数据和专家经验,得出升降系统发生故障的概率在7.63%到12.71%之间变化,这一结果与精确的概率值相比,更符合实际情况。
运用概率重要度计算方法,计算出各事件的概率重要度,得出对升降系统发生故障产生影响的各底事件重要度排序,这为工作人员进行维修或改进提供了指导方向。

