面向能源互联网的零碳园区智能感知设备优化规划方法

潘霄，张明理，韩震焘，胡旌伟，刘嘉恒，葛磊蛟

(1.国网辽宁省电力有限公司经济技术研究院，沈阳市 110015；2.天津大学电气自动化与信息工程学院，天津市 300072)

0 引 言

作为世界上最大的能源生产国和消费国，中国关于“双碳”目标的“时间表”与“路线图”一直备受海内外观察人士关注[1]。在应对全球气候变化挑战的背景下，以低能耗、低污染、低排放为基础的“低碳经济”已成为全球热点，也对电力能源安全运行提出了更高要求[2]。面向能源互联网的零碳园区以新能源为主体，汇集了高比例风/光/生物质等可再生能源、氢发电、煤电、核电等，是未来电力能源的主要承载形式[3]。

面向能源互联网的零碳园区对于园区的发展具有重要意义，相关的技术研究层出不穷[4]。文献[5]提出了一种基于多能互补的园区综合能源站-网协同优化规划方法，从站-网整体规划的角度出发，对能源站数量、位置和设备容量配置,供能网络布局进行统一规划研究；文献[6]从资源评估、负荷预测、综合能源系统建模、优化算法求解、区域供能站和管网规划原则等方面对园区级的综合能源系统进行详细的案例分析。文献[7]提出考虑能量梯级利用的园区综合能源系统站网协同规划方法，基于能量梯级利用原理,对能源站选址、设备选型定容和能源网络布局进行协同规划；文献[8]为了充分考虑园区综合能源系统的低碳性以及建设时序,提出了一种基于阶梯碳交易机制的园区综合能源系统多阶段规划方法。文献[9]通过基于分时电价机制，采取低谷储能峰平释能的运行策略动态调整冷负荷侧制冷机组功率和园区与电网联络线功率，由园区能量平衡原则得到储能系统的实时充放电功率,实现对储能功率和容量的配置；文献[10]搭建了园区能源互联网的典型架构,并对能源设备进行建模，构建了园区能源互联网双层优化配置模型，提出了计及多评价指标的园区能源互联网双层优化配置方法。

零碳园区的态势感知技术是其智能化、多样化发展的关键一环。态势感知技术是在大规模系统环境中，对能够引起系统态势发生变化的要素进行获取、理解、显示，并预测未来发展趋势等活动的一种技术[11]，流程可划分为态势觉察、态势理解、态势预测等3个阶段[12]。其中，态势觉察阶段主要是为了完成零碳园区数据或信息收集的任务，即获取并检测环境中的重要特征元素[13]。因此，如何合理规划零碳园区中用于数据收集与分析的智能感知设备，是保证零碳园区能源系统可靠、安全、优质、低碳和经济运行的焦点之一。

零碳园区中的智能感知设备是用于零碳园区数据采集和管理的新设备。然而，由于零碳园区的需要，收集信息的设备具有大规模、分散性和无序性的特点，且智能感知设备的昂贵价格，在每个零碳园区每一个需要监测信息的监测点都安装智能感知设备对于大规模应用来说成本过高且数据采集效率低。文献[14]为实现光伏智能边缘终端的合理优化配置，提出了一种基于改进郊狼优化算法的光伏智能边缘终端优化配置方法。文献[15]针对郊狼优化算法优化性能弱、可操作性低的问题提出了一种变异反向学习郊狼优化算法，以解决光伏智能边缘终端的优化配置。然而，在面向能源互联网的零碳园区的规划研究方面，目前的研究还没有考虑其智能感知设备的优化规划方面，因此，迫切需要建立面向零碳园区的智能感知设备优化规划方法的数学模型。

智能感知设备的优化规划模型具有高度的非线性与复杂性，智能算法是处理实际工程应用中复杂问题与非线性问题的有效解决方案，例如粒子群算法[16]、遗传算法[17]、樽海鞘优化算法[18]等。灰狼优化器(grey wolf optimizer，GWO)[19]是2014年提出的一种元启发式算法，它模仿了自然界中灰狼的等级制度和狩猎行为，具有较快的收敛速度和全局优化能力。然而，其算法机制是由种群中三头精英狼引导，尽管这使得算法快速收敛，但是其算法精度低，容易获得局部最优解。教与学算法(teaching-learning-based optimization,TLBO)[20]是一种模拟课堂教学过程的基于群体的优化方法。分为“教师阶段”(即向教师学习)与“学习者阶段”(即通过学习者之间的互动进行学习)，其两个阶段均为对候选解的评价行为，虽然使得算法求解精度高，但是求解速度与收敛速度均较慢。为此，本文结合两种算法的优点，提出灰狼优化器-教与学混合优化(grey wolf and teaching-learning hybrid optimization，GWO-TLBO)算法，以克服两种算法存在的各自缺点，保证准确、快速地获得面向零碳园区的智能感知设备的最优规划方案。

综上所述，本文提出一种面向能源互联网的零碳园区智能感知设备优化规划方法。首先，分析智能感知设备的规划要求，提出智能感知设备优化规划的数学模型。对于一个给定的零碳园区/低碳城市，文中的模型旨在获得智能感知设备的最佳数量和位置。然后，提出GWO-TLBO算法实现对智能感知设备优化规划模型的高精度求解。最后，以零碳园区为背景，针对点多面广、分散无序、数量庞大的零碳园区多类型设备的数据监测需要，实现智能感知设备的合理规划。

1 智能感知设备优化规划的数学模型

1.1 目标函数

1.1.1 投资成本

投资成本是所有规划问题中首先要考虑的因素，主要是购买和安装零碳园区智能感知设备的费用。零碳园区的智能感知设备的投资成本可以用以下公式描述：

(1)

A(r,ni)=r(1+r)ni/[(1+r)ni-1-1]

(2)

式中：CI是零碳园区的智能感知设备投资成本；N是智能感知设备的总数量；PT是一个智能感知设备在当前规划阶段的价格；A(r,ni)是资本回收系数；r是年利率；ni是区域内第i个智能感知设备的寿命。

1.1.2 故障损失成本

零碳园区的内部环境复杂多样，其中的智能感知设备容易出现故障，这种故障的出现会对两个方面造成影响。其一，智能感知设备的故障需要被修复从而产生维修成本；其二，由于智能感知设备产生故障，从而无法对零碳园区的态势进行检测，态势觉察受到影响，这也导致了需要弥补其不能工作的成本出现。首先，本文对零碳园区智能感知设备的故障率进行讨论：

智能感知设备的故障概率和使用寿命在理论上也是不同的，因此，本文提出一个结合的智能感知设备故障与使用寿命确定方法。单个零碳园区的智能感知设备的故障概率pi取决于它所监测设备的最大数量，可按以下方式计算：

(3)

同时，零碳园区中的智能感知设备的故障率将影响其智能感知设备的使用寿命，其数学模型为：

(4)

kj=Wj/WT

(5)

式中：nIN是一个智能感知设备的最大寿命；ω和σ是寿命系数；kj是第j个需要被监测设备智能感知设备的寿命系数；WT是参考值；Wj是零碳园区中第j个需要被监测设备的智能感知设备的寿命；S代表智能感知设备的集合。

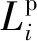
(6)

(7)

式中：LK是固定的维修次数；v是与维修次数有关的系数；ceil(·)是向上取整函数；T是智能感知设备的年工作日数。

零碳园区中的智能感知设备的故障具有随机性，为了分析故障损失的成本，有必要对智能感知设备的故障数量进行不确定性分析。在本文中，智能感知设备的故障率被认为是遵循指数分布的一个量，其概率密度函数可以描述如下：

f(xi)=piλie-λixi

(8)

式中：λi是该地区第i个智能感知设备故障的概率密度函数的参数；f(xi)是设备故障的概率密度函数。λi可以用下式计算：

(9)

如果智能感知设备发生故障，需要时间y来修复；根据已经存在的故障修复时间的研究，y也遵循指数分布，其分布函数为：

Fy=1-e-λyy

(10)

式中：Fy是设备维护的时间点的分布函数；λy是指数分布的参数。

描述智能感知设备故障导致其在时间t不可用的概率密度函数可以写成：

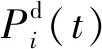
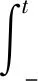
(11)

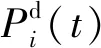
(12)

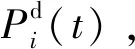
(13)

(14)

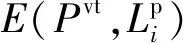
1.1.3 运营和维护成本

由于园区内架构复杂且范围较广，因此运维人员到达运维的智能感知设备地点的交通费用不可忽略，智能感知设备的年度运营与维护成本涉及运维人员的交通成本和劳动成本，其中的交通成本CG计算如下：

(15)

式中：CG是一个智能感知设备的年度交通成本；CM是智能感知设备和零碳园区中被监测设备的固有交通成本；M为需要被监测的设备数量；Aij是一个二进制变量：如果一个智能感知设备与一个需要被监测的设备建立连接，Aij=1，否则Aij=0；Rij是第i个智能感知设备和第j个需要被监测设备之间的距离；θ是一个与交通成本有关的常数系数；V是一个与通信连接成本有关的系数。

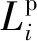
(16)

式中：u代表维修一个智能感知设备的成本；CC为智能感知设备的运维成本。

因此，目标函数表述如下：

minC=CI+CF+CG+CC

(17)

1.2 约束条件

零碳园区智能感知设备所能进行态势觉察的设备数量是有限的，但所有智能感知设备必须对园区内至少一种设备进行监测，此约束条件表示如下：

(18)

(19)

式中：Jmax表示一个智能感知设备与被监测设备的最大连接数量。

由于零碳园区的空间限制，智能感知设备的数量约束如下：

N≤Nmax

(20)

式中：Nmax为零碳园区中所布置的智能感知设备的最大数量。

智能感知设备与需要被监测的园区和城市设备的距离需要满足一定条件，以保证数据采集的准确性与运行维护的便利性，此约束条件被描述如下：

AijRij≤Rmax

(21)

式中：Rmax是智能感知设备和需要被监测设备之间的最大距离。

如果智能感知设备的寿命很短，那么智能感知设备将被频繁替换，智能感知设备的更换成本也不能被忽视。因此，智能感知设备的使用寿命不能低于规定值，计算公式如下：

ni≥nlim

(22)

式中：nlim为在零碳园区中所配置的智能感知设备的最短设备寿命。

2 智能感知设备优化规划的模型求解方法

2.1 灰狼优化算法

灰狼优化算法模仿了自然界中灰狼的等级制度和狩猎行为。在GWO中，灰狼个体被划分为α、β、δ、ω四个级别。最优解被设定为α狼，次优解为β狼，第三个最优解是δ狼，其余的解是ω狼。灰狼的捕猎过程包括接近和围捕猎物，狼群的围捕行为建模如下：

X(z+1)=XP(z)-A·D

(23)

D=|C·XP(z)-X(z)|

(24)

式中：D是个体狼与猎物之间的距离；C和A是系数向量；XP(z)是猎物的位置向量。X(z)是单只狼的位置向量。其中，A和C的计算公式如下：

A=2a·r1-a

(25)

C=2r2

(26)

式中：r1和r2是[0，1]之间的随机值；a是收敛因子，描述如下：

a=2-2t/tmax

(27)

式中：t是当前的迭代数；tmax代表最大迭代次数。

在狩猎阶段，灰狼在围住猎物后会更新自己的位置，如下所述：

(28)

(29)

X(z+1)=(X1+X2+X3)/3

(30)

式中：Dα、Dβ、Dδ是α、β、δ与其他个体之间的距离；Xα、Xβ、Xδ分别是α、β、δ的当前位置；C1、C2、C3和A1、A2、A3分别为α、β、δ的系数向量。

2.2 教与学优化算法

教与学优化算法是一种模拟课堂教学过程的基于群体的优化方法。TLBO分为两部分。第一部分是“教师阶段”，即向教师学习；第二部分是“学习者阶段”，即通过学习者之间的互动进行学习。

2.2.1 “教”阶段

在TLBO算法的“教”阶段，班级中每个学员根据教师的值Xteacher和学员平均值ME进行差异化学习：

(31)

(32)

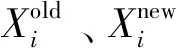
(33)

式中：NP代表种群数量。

2.2.2 “学”阶段

在“学”阶段，对每一个学员在班级中随机选取一个学习对象通过分析自己和学员的差异进行学习调整，TLBO算法中的学习步长对每个学员采用不同的学习因子：

(34)

式中：ri=U(0,1)表示第i个学员的学习因子(学习步长)；Xi和Xj分别代表种群中第i个和第j个学员。

2.3 灰狼-教与学混合优化方法

2.3.1 灰狼-教与学混合优化方法提出的动机

本文提出GWO-TLBO且应用于零碳园区智能感知设备的优化规划问题的求解方法的动机如下：

智能感知设备的优化要求是需要在有限的迭代次数内获得高精度的解，本文选取TLBO与GWO的结合作为零碳园区智能感知设备优化规划模型的求解算法的理由在于，相比于其他元启发式优化算法，TLBO与GWO具有其独有的特性，描述如下：

TLBO包含“教”与“学”两个阶段的搜索与更新方法，在“教”与“学”两个阶段均存在适应度计算与迭代更新，候选解位置的更新取决于教师(当前最优解)、学生的平均位置、随机的学生位置三种影响因素，其种群内个体不完全受当前最优解的引导，三种引导因素之间差异明显。因此相比于已有的元启发式算法，TLBO不容易陷入到局部最优中，可以获得高质量的规划方案，但TLBO的迭代过程具有迭代次数多且每一次迭代计算的时间较长的缺点。

GWO以三只种群中较好的灰狼为种群中其他灰狼的位置更新导向，其种群更新受到最优解(α狼)、次优解(β狼)与第三最优解(δ狼)的影响，尽管GWO与TLBO一样均受到三个不同因素的影响，但这三个因素均为种群中当前较优的候选解。在算法迭代前期，前三个最优解一般差异明显，但在算法迭代后期就会出现三个因素相同或者差异小的情况，非常容易导致算法陷入局部最优中。因此，相比于现有的粒子群算法、正余弦算法等元启发式算法，尽管GWO具有模型简单且具有快速收敛的优点，但其精度不能满足智能感知终端优化规划的要求。

综上，相比于其他已有的元启发式算法，TLBO具有非常高的求解精度，但迭代时间过长的特点，而GWO具有收敛速度较快，但非常容易陷入到局部最优解中的特点。因此，本文将TLBO与GWO相结合，提出一种GWO-TLBO的混合算法。GWO-TLBO克服了TLBO求解速度慢以及GWO求解精度低的缺点，具有精度高、收敛速度快的独特优势。

2.3.2 灰狼-教与学混合优化方法描述

下面对所提出的GWO-TLBO进一步解释：零碳园区智能感知设备的优化规划数学模型复杂，使用的优化算法需要有很强的全局搜索能力，且要求算法的迭代次数越少越好，迭代次数过多会造成时间和资源的浪费。根据以上对优化算法的要求，采用GWO和TLBO的组合可以很好地解决这一问题。GWO-TLBO算法的具体结合流程如下：利用GWO种群中排名前三的灰狼来更新其他灰狼的位置，使其他灰狼能够迅速与种群中的高水平灰狼同步，在有限的迭代次数中获得相对较好的优化结果。在这个过程中，GWO可以被认为是TLBO的初始化方法，进一步地，使用TLBO进行细化搜索，最终获得零碳园区智能感知设备的高质量规划方案。GWO-TLBO克服了GWO和TLBO的缺点的同时，继承了二者的优点，所以它符合本文的优化要求。GWO-TLBO的算法流程如图1所示。

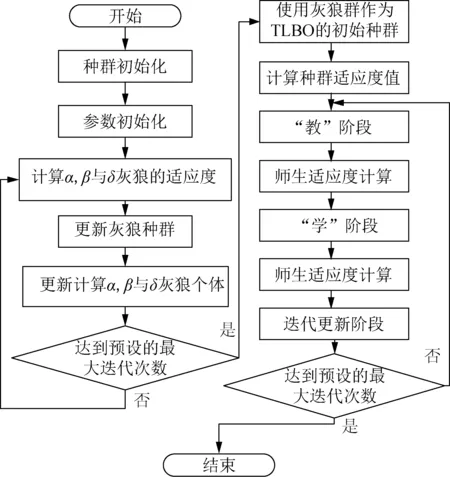
图1 GWO-TLBO的流程图Fig.1 Flowchart of GWO-TLBO

3 案例验证与分析

3.1 智能感知设备优化规划案例介绍

为了验证面向能源互联网的零碳园区智能感知设备优化规划方法的可行性，引入一个案例进行研究。面向能源互联网的零碳园区以新能源为主体，汇集了高比例风/光/生物质等可再生能源、氢发电、煤电等能源形式。因此，零碳园区中需要监测的设备类型不仅数量多而且复杂多样，具有分散、无序的特点。为了充分说明本文所提出的优化方法在不同尺度、边界条件和参数下的优越性，进行了几种不同的优化配置案例。数学模型中的参数如表1所示。

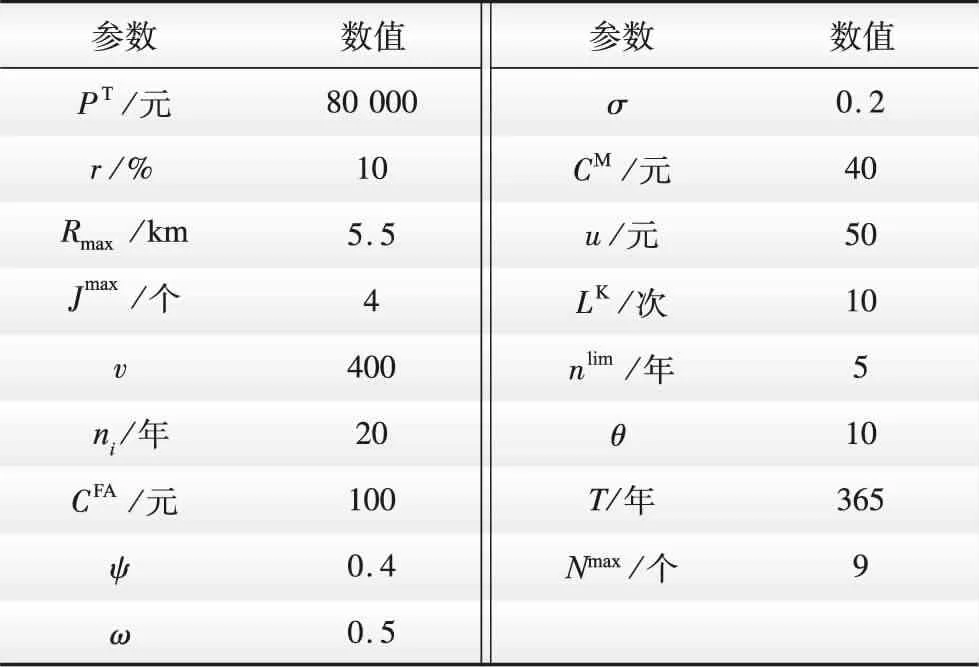
表1 零碳园区智能感知设备优化规划的数学模型参数Table 1 Mathematical model parameters for optimal planning of intelligent sensing equipment in zero-carbon parks

3.2 智能感知设备优化规划方法验证与算法对比

对于面向能源互联网的零碳园区智能感知设备优化规划，比较了4个不同规模的智能感知设备优化配置实例。将智能感知设备的最大数量表示为N，将需要监测的零碳园区多类型用户设备的数量表示为M。零碳园区多类型用户设备的最大数量的选择依据为N=M×0.3，更符合配置智能感知设备数量远小于零碳园区多类型用户设备数量的目标。之所以选择这些案例，是因为M从 40 到 100 的跨度较大，可以验证本文所提出规划方法在不同规模下的有效性。这也符合现实中小规模和大规模分布在一定区域内的区别，所设置案例如下：

Case 1(案例1):M=100,N=30;

Case 2(案例2):M=80,N=24;

Case 3(案例3):M=60,N=18;

Case 4(案例4):M=40,N=12。

在本文的案例分析中，仿真环境采用Intel(R)Core(TM)i7-6700HQ CPU，主频2.60 GHz和内存8 GB的PC机，操作系统采用64位的Windows 10，编程语言为MATLAB2017A。为进一步验证本文所提出的GWO-TLBO在面向零碳园区智能感知设备优化规划中应用效果，证明本文对算法作出改进与融合的合理性，将本文的GWO-TLBO与传统TLBO、正余弦算法(sine cosine algorithm，SCA)、GWO、粒子群算法(particle swarm optimization，PSO)、旗鱼优化器(sailfish optimizer，SFO)、海洋捕食者算法(marine predators algorithm，MPA)、象群算法(elephant herding optimization，EHO)进行比较，算法参数如表2所示。

表2 智能优化算法参数Table 2 Parameters of intelligent optimization algorithms

为公平起见，设定所有智能算法的预设最大迭代次数为50，种群数量为20。同时，为消除启发式算法随机性对其性能测试结果的影响，每个算法独立运行30次，并统计优化结果的均值(mean)、均方差(std)与最小值(min)，均值与最小值反映了算法的优化性能，均方差反映了算法稳定性。智能感知设备规划方案的结果对比如表3所示。

从表3中可知，对于本文所提出的零碳园区智能感知设备优化规划模型，相比于SCA、GWO、PSO、MPA、TLBO与EHO，本文所提出的GWO-TLBO方法获得的规划结果在4个案例中无论是在均值上还是在最小值上均展现出了最优的优化性能，获得了具有最低生命周期成本的规划方案。可见，GWO-TLBO显著提高了原算法处理智能感知设备优化规划的性能，并在效果上优于现有的多数元启发式智能算法。然而，GWO-TLBO也具有一定的不足：在稳定性上，TLBO的稳定性是最优的，GWO-TLBO的稳定性差于MPA和TLBO。这是因为GWO种群进化的质量仅取决三条最优狼引导，没有跳出局部最优的机制，导致算法本身并不稳定。在TLBO与GWO的结合时，GWO中的不稳定因素影响TLBO的稳定性，最终导致混合算法的稳定性较差。

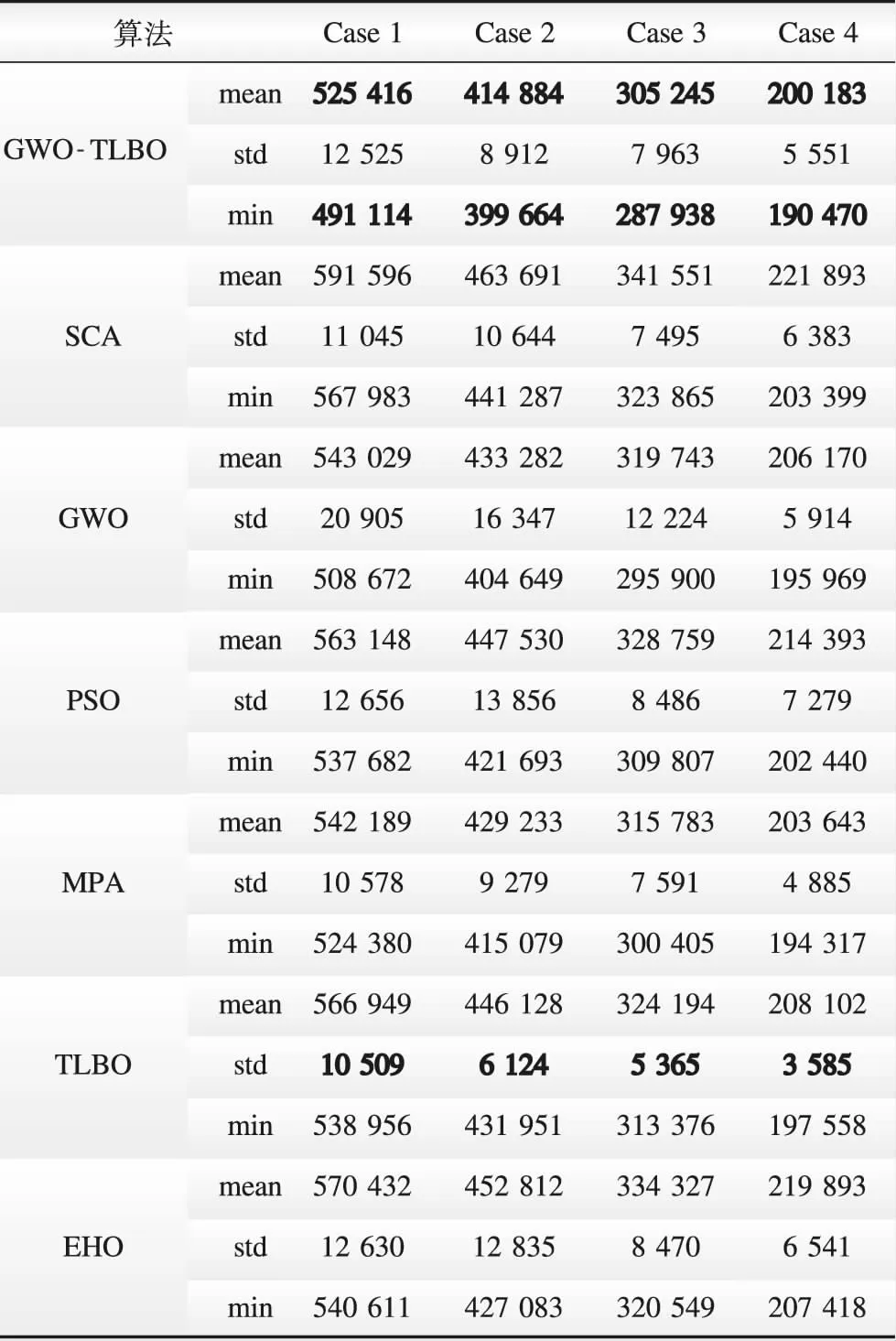
表3 智能优化算法求解结果对比Table 3 Comparison of solution results of intelligent optimization algorithms

若不采用本文所提出的优化配置方法，而是对于零碳园区内所有多类型用户设备都配置一台智能感知设备，那么案例1到案例4的规划成本分别为1 092 782元、874 226元、655 669 和437 113元，可见，无论采用何种算法进行智能感知设备的规划，无论是在大型零碳园区还是中小型零碳园区，本文的规划方法均可以显著降低生命周期成本。

为进一步验证本文所提出的GWO-TLBO在面向零碳园区智能感知设备优化规划中的收敛性效果，将本文的GWO-TLBO与TLBO、SCA、GWO、PSO、SFO、MPA、EHO的收敛性方案进行对比，结果如图2所示。值得注意的是，为了更好地表示智能算法的收敛性差异，在算法收敛性曲线中对所获得结果作对数处理。

从图2中各个算法的收敛性曲线可以看出，本文所提出的GWO-TLBO在处理零碳园区智能感知设备的规划时具有最高的精度和收敛速度。可见，GWO虽然很快收敛，但是很明显算法陷入了局部最优，获得的智能感知规划结果不能支撑其实际应用；TLBO的收敛曲线下降较快，但在迭代结束后都没有达到收敛状态，可见该算法虽然具有较强的全局寻优能力，但是其收敛速度较慢。GWO-TLBO的结合，利用GWO快速收敛的能力获得一个较好的解，再利用TLBO进行精细的搜索，可获得最优的智能感知设备规划方案。

图2 智能优化算法的收敛性曲线对比Fig.2 Comparison of convergence curves of intelligent optimization algorithms

4 结 论

为保证零碳园区可靠、安全、优质、低碳和经济运行，本文提出一种面向能源互联网的零碳园区智能感知设备优化规划方法。首先，分析零碳园区状态感知设备的要求，制定了智能感知设备优化规划的原则，考虑投资成本、维护成本、故障成本等方面，提出了零碳园区智能感知设备优化规划的数学模型；其次，为实现所制定数学模型的准确求解，提出一种灰狼优化器-教与学混合(GWO-TLBO)算法；最后，以一个零碳园区的实际案例作为仿真案例，验证了本文所提出的零碳园区智能感知设备优化规划方法能够显著降低生命周期成本，与现有智能算法的对比实验表明本文的GWO-TLBO算法具有最高的求解精度，本文的主要创新点如下：

1)目前零碳园区一次系统的规划研究很多，但对于二次系统的规划技术却鲜有研究，为此，本文提出了零碳园区智能感知设备的优化配置模型，构建了优化配置的数学模型；

2)为实现所制定数学模型的准确求解，提出一种GWO-TLBO算法，与现有智能算法的对比实验表明所提出的GWO-TLBO算法具有较高的求解精度。

本文的优化规划问题为单目标优化问题，仅保证了感知设备规划的经济性目标最优，在实际工程应用中具有一定的局限性。在未来的工作中，将考虑低碳园区中智能感知设备规划经济性、安全可靠性、低碳性等方面，开展智能感知设备多目标优化规划研究，使提出的规划设计方案更加具有现实意义。此外，在智能感知设备的优化规划中考虑零碳园区内的地理环境信息也是一个十分有意义的研究方向。