家具装配线人机任务分配问题研究

■郝绍平，陶 涛,2,3，戴向东，黄艳丽，陈星艳,2,3，欧阳周洲，王 迅，詹秀丽，吕 宙

(1.中南林业科技大学，湖南长沙 410004；2.农林生物质绿色加工技术国家地方联合工程研究中心，湖南长沙 410004；3.木竹资源高效利用省部共建协同创新中心，湖南长沙 410004）

随着“中国制造2025”国家战略的实施，我国的人工智能技术得到了迅猛的发展，各制造企业纷纷尝试运用更多的机器人以及自动化设备来代替成本越来越高的劳动力[1]，以求达到无人化生产的目标。但全自动生产系统不够灵活，简单的“机器换人”并不适用于所有制造业企业[2]。家具作为传统制造业，生产工艺环节繁多且连续性强，某一局部故障引起的变化会波及整个生产系统的运行，且风格多元化、需求个性化、产品单件化导致家具制造工艺复杂多样，这些特点要求生产系统具有更大的灵活性[3-4]。其中在家具生产制造中，产品的组装与装配工序占产品生产工作量的70%，装配时间占总生产时间的60%。由于自动化的装配生产线不够灵活，不能满足产品变化的需求，而手工装配生产线缺乏效率和精度。因此，若能通过好的方式与策略，把人和机器的优势相结合，充分发挥人的认知能力，并运用机器强度大、精度高、持续性强的优势，将家具装配任务合理地分配给人与机器，对实现人机协同、提高生产效率、促进家具企业的转型，都具有十分重要的意义。本文尝试通过建立家具装配系统人机任务分配模型，采用量化评估的方法，确定合理的人机协同方式，构建人机共融的家具智能装配系统，以提升生产制造的弹性、灵活性和可持续性。

1 家具装配线人机任务分配依据

在人机协作中，应充分发挥作业人员与设备的作用，以实现成本的最小化和生产效率的最大化，因此人机任务分配问题成为人机协作面临的最大挑战。将任务合理地分配给人与机器需要全面衡量和分析人和机器的特点，科学合理地将装配线中的任务以一定的规则分配给人与机器，让人和机器的长处和优势得到最大化的利用，从而使人机生产系统具有稳定性的同时，其最大生产效能也可以最大限度地发挥。关于人与机器的关系，研究大致经历了几个阶段：人适应机器、机器适应人、人与机器之间相互适应,人机协作是目前研究的重点[5-6]。对于人与机器各自的特性，经典的Fitts表（表1）[7]对其进行了描述，从表中可知，机的能力相对稳定，可以由机器来完成单调重复、负荷大、需连续操作等特点的任务，人的能力具有灵活性，可以由人来完成需要判断、决策、变化频繁等特点的任务。

表1 Fitts人机能力对比表

对于不同任务，人和机器的不同特性在一系列需求指标下表现出不同的特性，但Fitts表[8]主要分析了人与机器各自的优势与擅长领域，而关于人机各自的优势对各种任务的满足程度没有直接的表现。因此，在对人机任务分配之前需要先明确任务的特点，根据任务的特点确定评价的指标。对任务特点的分析是对家具装配线规划的前提和重要基础，同时也会对家具装配线的规划产生约束条件。对任务特点的分析主要包括完成任务的效率与时间、规划产线的成本、人的疲劳度等，因此进行合理的人机任务分配需要综合考虑多方面的因素。基于此，本文通过多目标模糊决策的数学方法对人机任务进行合理分配。

2 家具装配线人机任务分配

2.1 家具装配线人机任务分配模型

在对家具装配线进行设计或改造时，以提高家具装配线生产效率为目标。为实现这一目标，本文在进行装配线人机任务分配中，假定将所有的任务都分配给各个资源，并以此为前提，提出一个流程模型对任务分配进行描述。图1为人机任务分配流程图。

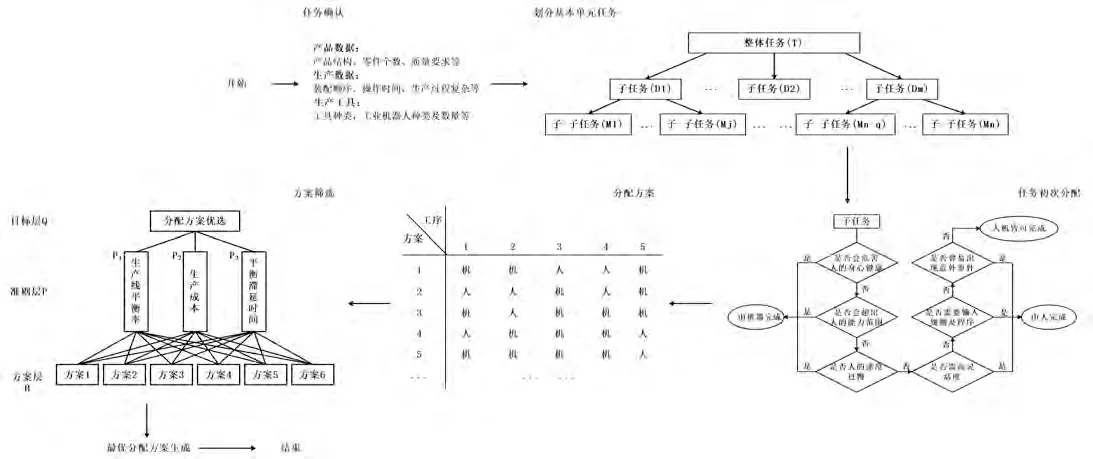
■图1 人机任务分配流程图

人机任务分配流程模型主要包括以下几个过程：

（1）任务确认

当进行任务分配时，通过对任务确认，确定产品数据（包括产品结构、零件个数、质量要求等）、生产数据（包括装配顺序、操作时间、生产过程复杂度等）、生产工具（包括工具种类、工业机器人种类及数量等），有利于对任务进行细化和评估。

（2）划分基本单元任务

划分基本单元任务作为设计装配线的重要环节，其目的是把整个任务分解成不可再分解的子任务[9]。划分基本单元任务流程根据图1所示，整体任务最终可以分解为不可再分的子任务集M（M1，M2，M3，… ，Mn），即每一个不可再分的子任务都可以由人或机器单独完成。对于不可再分的子任务的上一级任务则可以由人机协同完成。如图1中不可再分的子任务M1是由人完成，MJ是由机器完成，则子任务D1就是人机协同完成。家具装配线设计中，整体任务就是对家具进行装配的任务；以板式定制家具为例，其子任务包括齐套、发板、组装、质检等；其中组装又包括上料、定位、夹紧等。

（3）任务初次分配

根据任务执行的一些定性的约束条件，如是否由机器完成成本过高、是否容易出现意外事件、是否需要输入规则及程序等，对各子任务定性分析并初次分配，得到可行的家具装配线人机任务分配方案。

（4）方案筛选

评价指标的选择直接关系到最终分配方案的优劣。针对家具装配线，以生产线均衡度、生产成本、平衡滞延时间为评价指标[10-11]，用模糊层次分析法对方案进行评估优选。

①生产线均衡度：指装配生产线上各个生产环节作业时间的均衡程度，目的是为了防止某些资源的工作时间太短或某些资源的工作量太大，其定义为：

式中，成本计算所用参数的定义在表2中列出。

表2 成本计算所用参数的定义

③均衡滞延时间：是指每个工作资源的工作时间与需求时间之间的差异之和。

在公式中，C为需求时间，第n个工作资源的工作时间表示Pn，n指装配生产线上所有的组装资源的数量。

2.2 任务分配模型优选求解

模糊层次分析法( FAHP)[14-15]把人的主观判断过程思维化，同时有效地减少决策过程中需要量化的信息，并用模糊数值对不易量化的信息进行量化，可实现多目标、多准则的人机任务分配决策，具体的步骤是：

（1）多层梯阶结构模型的构建

根据研究对象，以及所确立的评估指标，构建一种多层次的梯阶结构模型。

（2）模糊互补判断矩阵R的建立

①以第一行中的每个元素为判定标准，以此为依据对其后每行元素进行两两对比，并定量分析，从而可构建出一个模糊互补矩阵。

②模糊互补矩阵R

该元素A同下一行中的各个元素Bi（i=1,2,...,n)相关联，模糊互补矩阵见表3。

表3 各模糊互补矩阵R

③在表格中，bij指元素Bi与元素Bj和前一行元素A进行对比时，元素Bi与元素Bj之间存在模糊关系的模系“重要程度”的隶属度。以数字0.1～0.9为标准进行度量，标度数值的含义如表4所示。

表4 各个标度值的含义

（3）检验

通过对获得的模糊互补矩阵R的一致性进行检验，将其转换为模糊判断矩阵，该方法的具体过程如下：

■图2 定制家具组装流程图

①首先对b11,b12,...,b1n进行对比与判断，并根据相对程度量化: 0. 1 ～ 0. 9;

②然后检查各行相应元素之间差

如果成立：

反之，按照以上公式的要求调整bij。

用模糊互补矩阵R的第一行元素减去第二行相对应的元素，如果得到的n个差数是常数，那么第二行元素不需要调整。反之，调整第二行元素直至第一行的元素和第二行对应元素的差是常数为止。

③最后进行检验

对式（4）进行调整后，对最大的特征根 求解，如果满足：

对各个方案的排序需根据Ti的大小，如果T1≧T2≧....≧Tn，则人机任务分配方案从优到劣的顺序是：B1≧B2≧....≧Bn。

3 实例分析与验证

3.1 案例概况及任务的分配

以定制家具E公司的家具装配系统为案例背景，通过任务分析及对现场进行观察测定，将该装配系统子任务分为齐套、发板、组装、质检、包装，下面以组装线的人机协作问题为例进行阐述。其组装流程如2图所示，共有7个工序，10个工人，1台组框机。

根据任务初次分配流程，进行初次分配。由于人对柜体压紧会出现柜体受力不均现象，因此将压紧工序分配给机器；因定制家具的产品样式多且门铰需调试，组装要求更灵活，从而将装配五金件、百货与门板工序分配给人。又由于组装柜身的设备为一体的，组装侧板、顶底板、背板工序所用劳动资源须一致，最终得到6种可行的任务分配方案（表5）。

表5 可行方案

3.2 方案的评价与筛选

（1）根据现场测定数据，按式（1）～（3）对5种可行方案的生产线均衡率、每小时生产成本、均衡滞延时间统计计算如表6所示。

表6 各方案评价指标统计值

（2）建立多层次的梯阶结构模型

以生产线均衡率、生产成本、均衡滞延时间作为评估各个人机任务分配方案的指标，构建定制家具组装线人机任务分配多层梯阶结构模型如图3所示。

■图3 定制家具组装线人机任务分配多层梯阶结构模型

（3）互补矩阵的构建

①根据表4各个标度值的含义，以准则层三项指标的计算结果表6为前提，对各方案B1～B6进行比较，可得到互补矩阵R1～R3如下：

②互补矩阵R

对准则层的各项指标进行比较，则模糊互补矩阵R:

根据以上计算可得：T5＞T4＞T1＞T2＞T6＞T3,则B5＞B4＞B1＞B2＞B6＞B3，从而方案5为最优方案。

（7）最优方案合理性分析

方案5只是在原生产方案的基础上增加了协作机器人，将工序2与工序6由人工完成变为由机器完成。从表6各方案评价指标值可得，方案5相较于原生产方案（方案1）生产线平衡率提高了1.2%，平衡滞延时间减少了10.3%，每小时生产成本增加了6.4%，其各项指标值未必是最优的，但其综合评价指标值比原生产方案提高了24.5%，充分利用了机器和工人的各自优势，提高了组装线的柔性及生产效率。

4 结语

本文以家具装配线为研究对象，分析生产车间人和机器的特点、功能，构建了以产品数据、生产数据、生产工具等为基础进行任务分配的人机任务分配模型，运用FAHP法以生产线平衡率、生产成本、平衡滞延时间为约束求解该模型，确立最优生产方案，最后通过实例验证表明本文提出的人机任务分配模型在对产线升级规划中确定合理的人机协作方式具有可行性。