异常性检测算法在引信干扰信号识别中的应用
白帆,张慧,李鹏斐,曹昭睿
(1.沈阳理工大学 a.装备工程学院 b.机械工程学院,辽宁 沈阳 110159;2.北京理工大学 机电学院,北京 100081;3.机电动态控制重点实验室,西安 710065)
随着通信技术的发展,引信干扰技术[1-2]日趋成熟,且随着现代作战环境的不断变化,该技术呈现出智能化、复杂化的发展趋势,干扰信号的类型、手段、策略也更为多样[3-4]。为了保证对引信信号的准确接收,引信抗干扰算法必须在极短的时间内,高效完成干扰信号检测、识别、过滤等任务,才能满足现阶段引信系统在复杂含扰环境下的有效工作需求。否则,引信系统极易在多种类、多策略干扰信号的影响下出现早炸、错失、误炸等问题,进而导致武器系统失效。
引信干扰信号的识别是一个复杂的非线性过程,往常以机器学习作为核心检测方法[5-6]。近年来,随着人工智能的发展,研究人员开始将卷积神经网络引入信号识别领域中[7-8]。郭治锐等[9]提出了基于改进的AlexNet 的雷达干扰识别方法,该方法利用AlexNet卷积神经网络自动提取雷达信号图像中的特征细节,以实现雷达干扰信号的分类识别。唐陈等[10]采用残差卷积神经网络,提取了各干扰的联合特征,完成了干扰信号的分类。刘国满等[11]设计了一种双卷积神经网络级联结构,基于单周期时频图像完成了干扰预分类,再利用多周期合成时频图像完成细分类,最终实现了8 种典型干扰样式的识别。魏迪等[12]考虑到传统卷积很难提取信号的时序特征,因此提出一种长短时记忆网络(LSTM)和特征融合的识别方法,对通信干扰进行了分类。毕明雪等[13]利用CVAE 算法生成了信号的时频谱图,并配合卷积神经网络对信号特征进行了提取,最后经由LSTM 网络对信号进行了识别。
然而,因真实引信干扰信号样本生成成本高,且难以获取[14-15],导致在实际引信抗干扰训练任务中很难对充足的干扰数据进行收集和标注。同时,引信干扰信号样本远小于正常信号样本,这种数据分布状态不利于监督学习。在网络训练的过程中,数量匮乏且分布不均的样本极易导致网络特征提取失衡,进而影响最终的计算精度。因此,为了有效增强引信抗干扰算法的计算能力,不但需要从网络原理的角度去提升算法的计算精度与速度,还需要降低网络对真实样本的依赖。
针对上述问题,本文引入异常性检测[16-17]算法,设计基于GANomaly-EfficientNet 的引信干扰信号识别算法(GE-FS),在小样本训练基础上,对干扰信号进行分类识别,提升引信抗干扰网络特征学习的泛化性、高效性与适配性。通过实验证明,GE-FS 算法能够有效增强引信异常性检测效果,可以综合提升引信的抗干扰能力。
1 引信数据前处理
1.1 含扰引信数据增强
由于真实含扰引信信号数据集难以获取,且制作成本较大,为确保网络模型在训练过程中能够获得足够强的泛化性,本方案采用原理如图1 所示的引信干扰信号数据增强方法对实验数据进行预处理,以扩增引信样本数量。如图1 所示,GE-FS 首先将读取到的全局数据以1×1 024 的尺度按顺序进行分割,随后对每个分割出的数据按照8×128 的尺度进行再分割,生成8 组尺度为128 的数据后,将其随机打乱,合成为一组尺度为1×1 024 的倍增数据,该数据将作为后续网络训练的输入数据源。通过这一方法,可以在不采集新的含噪引信真实样本的前提下,充分利用已有的小样本进行数据扩增,保证了模型的泛化能力。

图1 引信样本数据增强方法原理Fig.1 Principle of fuze sample data enhancement method
1.2 数据处理
初始采集的引信信号一般为一维时序信号,该类型信号维度较低,特征较少。为了得到引信信号的更多特征,本文将构造时间和频率联合函数,基于信号在不同时间、不同频率的能量密度或者强度,从时域和频域角度分析一维引信信号,即Wigner-Ville Distibution 时频分析方法[18]。利用时频分布[19-20]来分析一维引信信号,能得到其各个时刻的瞬时频率及其幅值,具体计算过程如下。
Wigner-Ville 分布可以看成信号的瞬时自相关函数的傅里叶变换,其表达式如(1)所示。

整理后如式(3)所示。
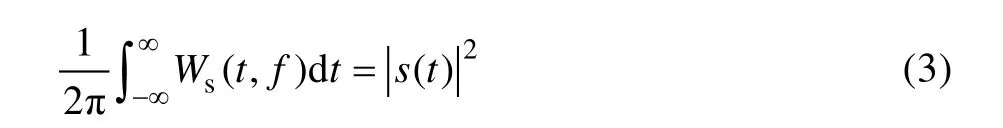
WVD 在某一频率段内对f进行积分,结果为该信号在t时刻的瞬时能量。同样,信号s(t)的傅里叶变换S(Ω)的WVD 可表示为式(4),结果为信号在Ω时刻的瞬时能量。
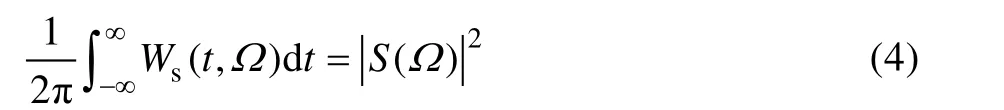
2 GE-FS 信号识别算法
2.1 GE-FS 信号识别算法总体设计
基于GANomaly-EfficientNet 的引信干扰信号识别网络(GE-FS)结构如图2 所示。GE-FS 主要由异常信号检测与干扰信号分类2 部分构成。待检测信号经WVD 变换后,得到时频谱图X时,GE-FS 首先将图片X输入信号异常检测部分,判断图片X是否为异常图片。若图片X为正常图片,则直接输出此时信号的类型为正常信号(Normal);若图片X为异常图片,则认为此时的输入为干扰信号,此时开启干扰信号分类部分,通过EfficientNet 实现干扰信号的分类。
图2 GE-FS 网络结构Fig.2 GE-FS Network structure
2.2 基于GANomaly 的信号识别算法
GANomaly 的网络结构[21-22]如图3 所示,主要由以下3 个部分组成:第1 部分为生成器部分,该部分通过编码器学习输入数据X的特征,输出中间向量Z,然后通过解码器重建输入的图片X',X与X'间通过损失函数1 控制收敛;第2 部分为编码器部分,该部分编码器的结构与生成器编码器部分的网络结构相同,但网络参数不同,因此生成器编码器的输出Z与Z'的维度及大小相同,Z与Z'间通过损失函数2 控制收敛;第3 部分为判别器部分,其目标为判断输入判别器X及X'的真假,此时采用损失函数3 控制收敛。
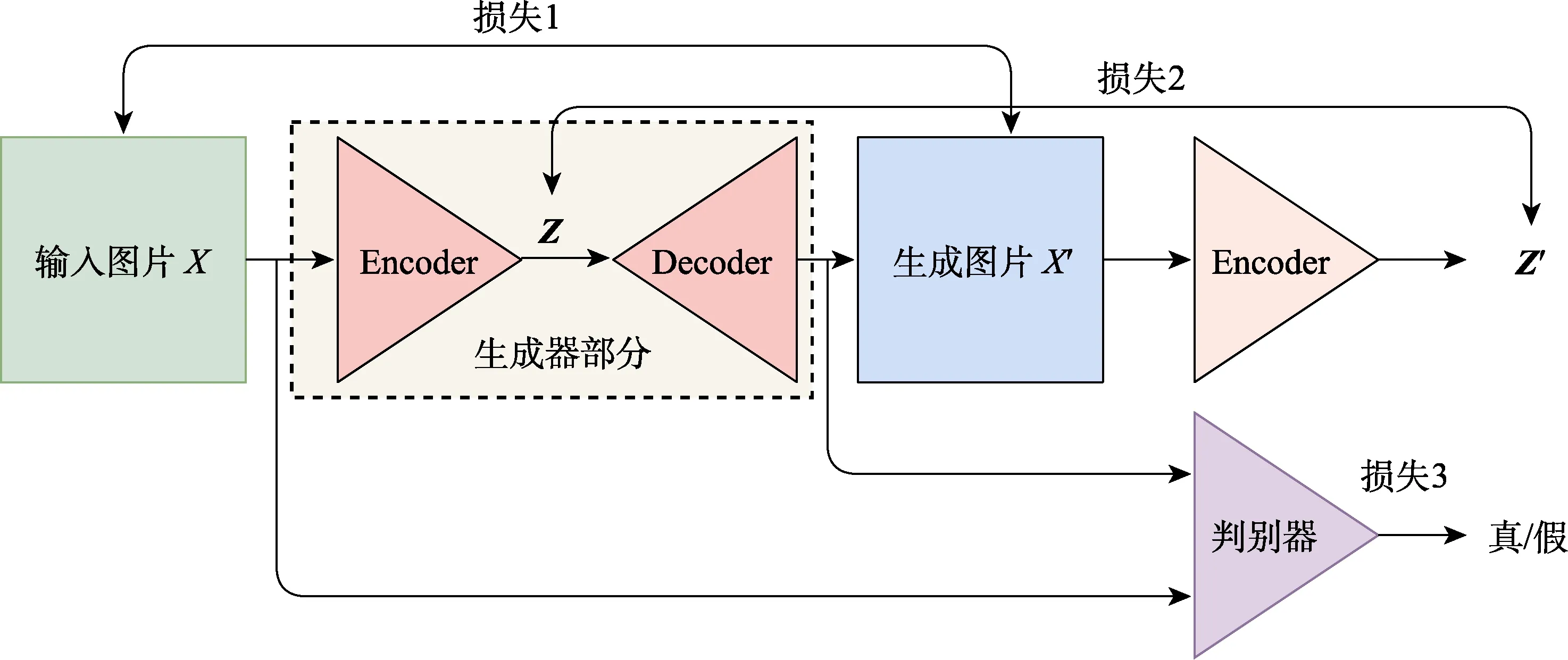
图3 GANomaly 网络结构Fig.3 GANomaly Network structure
在完成网络训练之后,使用GANomaly 异常检测算法进行模型测试时,其具体流程如图4 所示。输入图片X首先通过生成器生成图片X后,再将X'输入至编码器中,比较Z与Z'的差异。如果Z与Z'的差异较大,则认为此时的输入为异常输入;若Z与Z'的差异较小,则认为此时数据为正常数据,即为该类别信号。
第三,因人施教,降低难度和要求,培养学习兴趣。运动心理学教科书这样写:“兴趣是在需要的基础上,通过学习实践活动逐步形成和发展起来的。”因此,教师在选用大纲内容、教材搭配,教学进度和教学方法时,要充分考虑后进生的心理需要和实际能力(体质状况、接受能力)。力争每节课都做到活泼、新颖,多采用游戏和比赛法,使运动活动产生愉快的肌肉满足感。在练习和考评难度较大的项目时,教师的动员讲解要生动、清晰、幽默;态度、语气要有利于调动、稳定和激发学生情绪。对后进生的练习、要求和标准要放宽,作好保护与帮助,只要他们表现出有参与的欲望,完成动作后便马上给予肯定和鼓励。这样,他们才能逐渐在体育活动中产生积极心理状态。
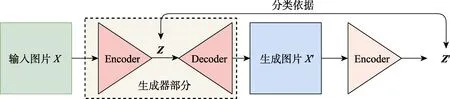
图4 GANomaly 检测流程Fig.4 GANomalydetection process
2.3 EfficientNet 网络结构
为了提高信号识别的准确率,本文将使用同时增加了网络宽度、深度以及分辨率的EfficientNet[23]作为干扰信号分类网络,其结构[24-25]如图5 所示。网络中每个阶段最前面的数值表示该阶段的重复次数,而每2 个阶段中间的数据为当前数据尺度。例如,第3阶段的“2×MBConv6,K3×3”表示由2 个大小为3×3卷积核构成的MobileNet Conv(MBConv)层,次层的输入数据尺度为 16×112×112,输出数据尺度为24×112×112。
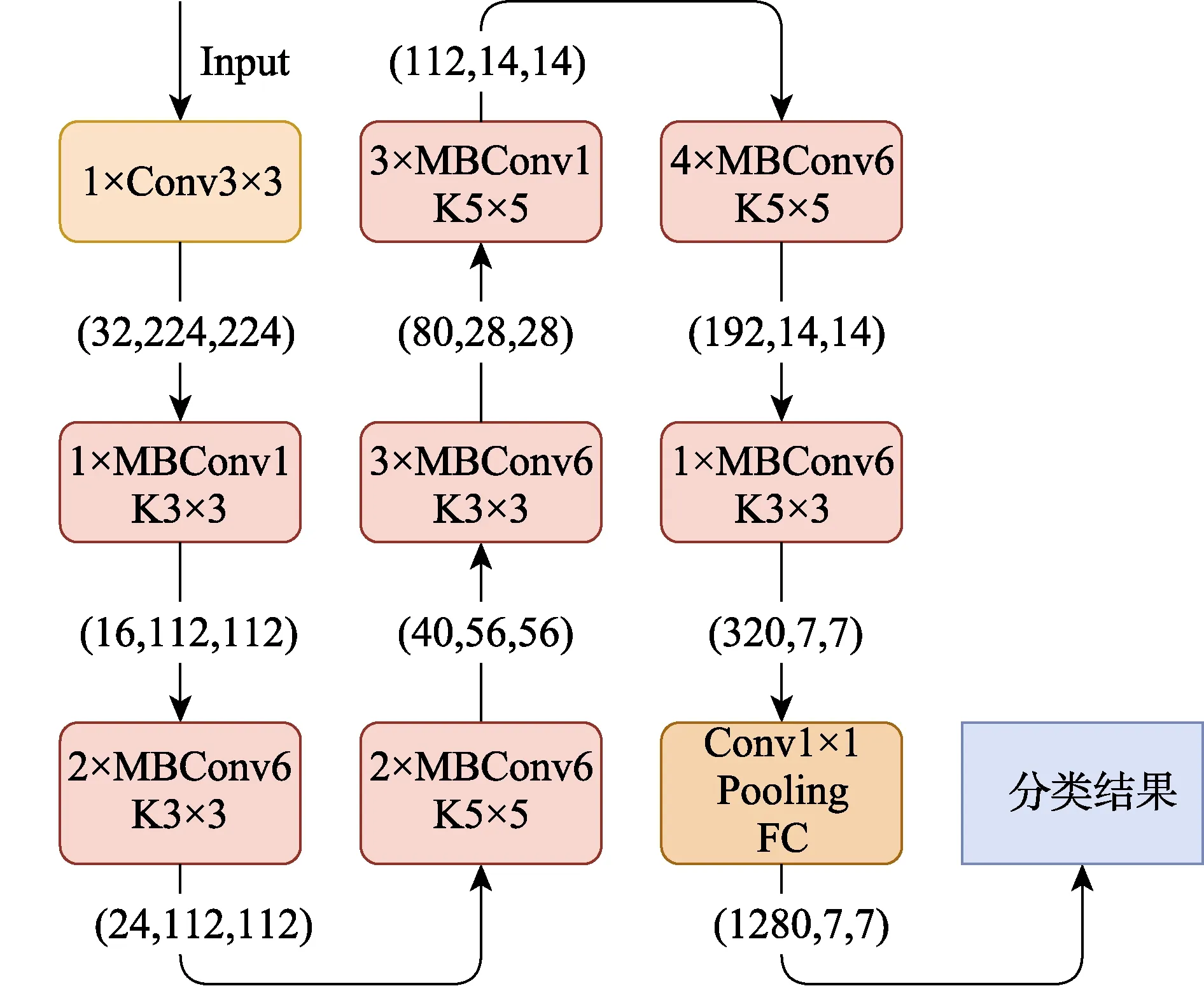
图5 EfficientNet 网络结构Fig.5 EfficientNet Network structure
EfficientNet 的输入图片尺度为3×224×224,依次经过如图5 所示的9 个阶段,其中第2—8 个阶段(Stage)采用重复堆叠的MBConv 层,其具体结构如图6a 所示。输入MBConv 层的特征图经1×1 的卷积核进行下采样计算,并采取批量归一化操作,随后利用Swish 激活函数升维。然后输入DW 卷积层中,同样采取批量归一化操作与Swish 激活函数计算,之后输入结构如图6b 所示的SE 层中。该层首先对于输入特征图的每个维度进行平均池化,然后分别通过2个全连接层FC1 和FC2,其中FC1 用Swish 激活函数,FC2 采用Sigmoid 激活函数。另外,FC2 的结点个数必须与输入特征图的维度保持一致,而FC1 结点个数等于输入特征图维度的1/4。经过SE 模块后,网络通过一个1×1 的卷积核实现降维,并通过Dropout操作剔除冗余计算。最后,网络将上述操作的输出与输入MBConv 层的特征图相加,以获得最终输出。
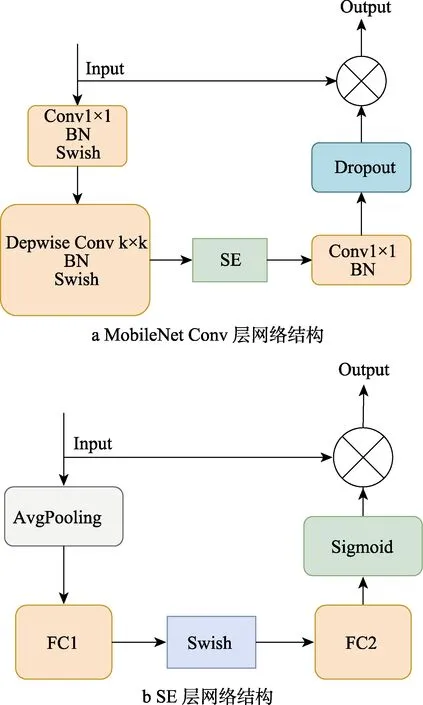
图6 EfficientNet 网络层结构Fig.6 Network layer structures of EfficientNet: a) Mobilenet Conv layer network structure; b) SE layer network structure
2.4 损失函数
GE-FS 网络共有4 个损失函数,在训练异常性检测网络时,共需要3 个损失函数。首先是上下文损失,通过衡量输入数据X与生成器生成的数据X'的误差损失来学习输入数据中的上下文信息,其表达式如式(5)所示。

其次是编码器损失,上下文损失起到保存数据的上下文信息,以及让生成的数据更加真实的作用,而编码器损失的作用是为了使Z与Z'之间的距离最小,其表达式如式(6)所示。
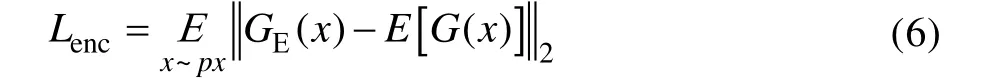
异常检测部分的最后一个损失为对抗损失,该损失采用使用特征对齐损失函数,其表达示如式(7)所示。
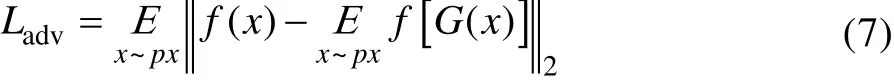
对抗损失通过计算输入图像与生成图像特征表达之间的欧氏距离,得到判别器的中间层向量,可以优化图像特征之间的差异。
最终,GE-FS 网络的异常检测算法损失函数如式(8)所示。
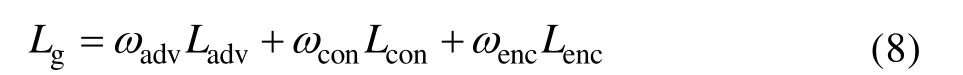
干扰信号分类部分的任务本质上为图像分类任务,因此损失函数为多分类交叉熵损失函数,可表示为式(9)。
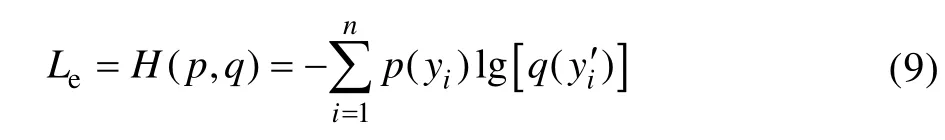
综上所述,GE-FS 算法的损失函数可表示为式(10)。

3 实验分析
3.1 数据处理
文中采用的引信样本为仿真数据,其中共4 类干扰信号以及1 组正常信号。第一类干扰的实验数据如图7 所示,总长度为32 034。
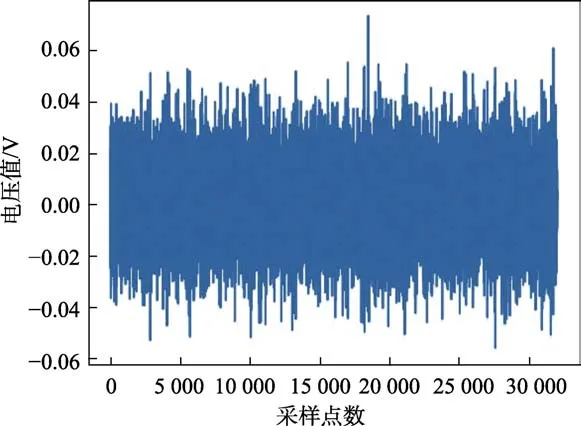
图7 一维时序干扰信号Fig.7 One-dimensional temporal interference signal
本次实验首先将读取到的信号数据以1×1 024 的形式按照顺序进行分割,随后将其作为网络训练的测试集。由于数据量较少,按照图1 所示的数据增强算法处理后,各类数据的数量见表1。
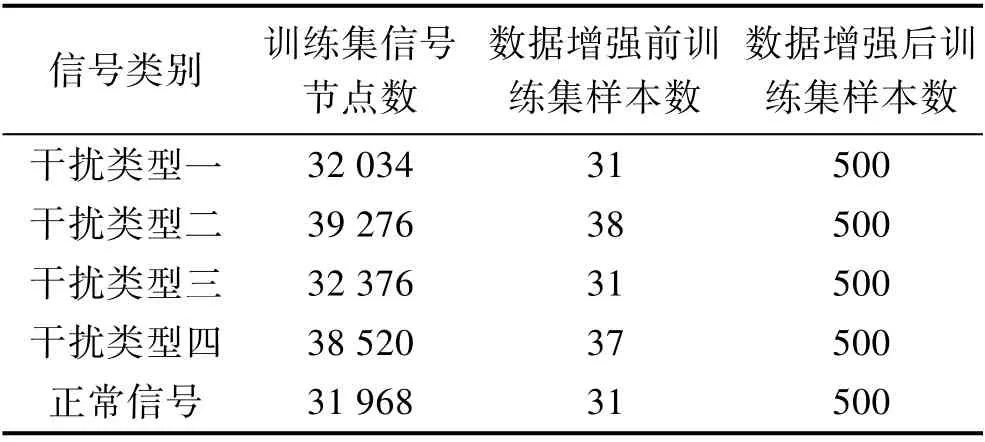
表1 数据增强结果Tab.1 Data enhancement results
完成数据增强后,采用WVD 算法对信号进行时频分析,将生成的时频谱图保存,并作为测试GE-FS算法的数据集。图8 为分别对5 种类型进行WVD 变换得到的时频谱图。
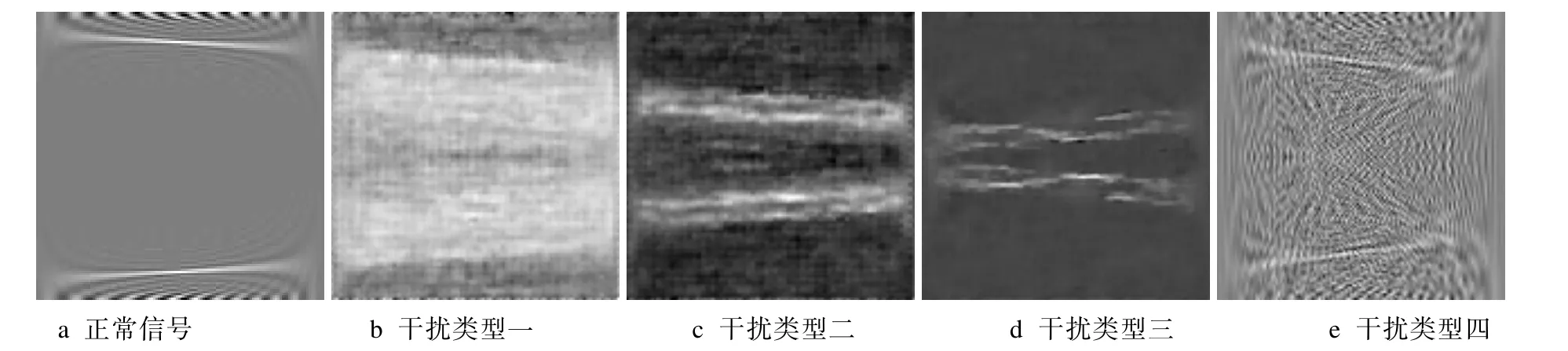
图8 5 种类型信号经WVD 变换后的时频谱图Fig.8Time spectrum diagrams of five types of signals after WVD transformation: a) normal signal; b) interference type 1; c) interference type 2; d) interference type 3; e) interference type 4
3.2 结果分析
为了验证GE-FS 算法的可行性,本文以联想R7作为验证计算机平台,其CPU 配置为AMD Ryzen7 4800H(主频为2.90 GHz),GPU 为GeForce GTX 1650 Ti(运行内存16 GB),计算环境为Windows 10,算法编写语言为Python3.7,并配合pytorch1.7 作为辅助高级API。实验结果见表2。
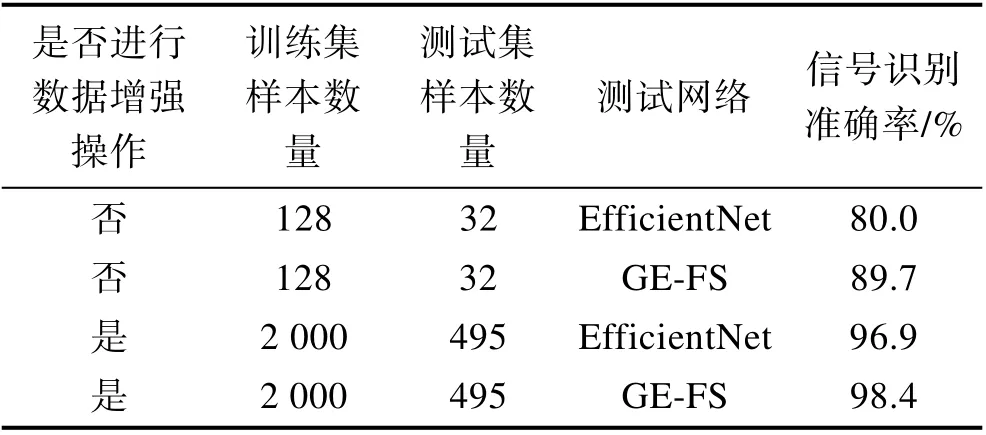
表2 实验结果Tab.2The experimental results
通过表2 可知,在均未使用数据增强算法的小样本条件下,基于EfficientNet 的信号识别分类算法的识别准确率为80%,而GE-FS 算法的识别准确率为89.7%。在使用数据增强算法后,EfficientNet 的信号识别分类算法的识别准确率提升为96.9%,而GE-FS分类算法的识别准确率提升为98.4%。该结果既证明了数据增强算法的有效性,也证明了GE-FS 干扰信号分类算法的性能优于传统基于卷积神经网络的识别分类算法,验证了异常性检测算法在引信干扰信号识别中应用的可行性、实用性与高效性。
4 结论
本文通过GE-FS 算法对扩充引信信号异常性检测测试,得出了以下结论:
1)基于WVD 时频转换的数据扩展方法能够对小样本真实含扰引信数据进行有效倍增,扩增的数据样本能够为干扰识别网络提供良好的训练基础,能够降低传统引信抗干扰算法对真实数据的依赖。
2)GE-FS 在扩增的仿真引信数据上具有良好的干扰检测能力,相比单架构引信抗干扰网络的信号识别,准确率具有较强提升。
综上所述,该算法在引信抗干扰任务中具有较强的应用价值,能够增强引信系统面向复杂作战环境时的抗扰能力与自适应性。

