三种数学模型模拟不同播期小麦籽粒灌浆过程的比较分析
王 珂,杨 娜,席吉龙,杨志国,王 健,张建诚
(1.山西省农业大学棉花研究所,山西运城 044000; 2.省部共建有机旱作农业重点实验室(筹),山西太原 030031)
小麦籽粒灌浆过程对小麦产量和品质有重要的影响[1-3]。小麦籽粒干物质的积累过程呈“S”型曲线,目前通常用Logistic方程、Richards方程、和三次多项式(Cubic)方程对其进行模拟,以描述籽粒灌浆的基本特征[4-9]。Logistic方程有3个待拟参数,Richards方程和Cubic方程均有4个待拟参数,通过这些参数可确定灌浆不同阶段的灌浆速率、持续时间等灌浆特征参数,其中Cubic方程可以通过计算极值确定灌浆起始期和终止期,Logistic和Richards方程灌浆起始期需要通过实际观测确定,终止期需要通过规定粒重达理论最大粒重的比例确定。有学者认为,Cubic方程参数没有明确的生物学意义,不适合植物生长过程的模拟[10-11];Logistic方程可塑性较差,且模型参数的生物学解释存在困难[12-13],但由于Cubic方程和Logistic方程的建立和检验比较成熟,所以在农业科研中应用广泛。许多研究表明,Richards方程更适合描述“S”型生长曲线[14-15],但其不能进行线性化处理,且参数值范围大,不利于模型方程参数的确定。对于不同模型对小麦籽粒灌浆过程的拟合程度,前人研究结果不一致,如蔡庆生[16]认为,Cubic方程比Logistic方程拟合程度更好,而薛香和孟兆江等[17,18]提出Richards方程拟合效果最好,能更好地反映品种的灌浆特性。近年来由于全球气候变暖、茬口紧张或播前降雨多等因素的影响,小麦播期推迟在生产中十分普遍。播期是影响小麦籽粒灌浆特性的重要因素之一,不同播期下小麦籽粒灌浆特性不尽相同[19-21]。前人关于不同播期籽粒灌浆模型多采用单一的数学模型[19-20]。为更准确模拟不同播期小麦籽粒灌浆过程,探究不同模型的特点,本研究用Logistic、Richards和Cubic 3种模型分别模拟4个小麦品种在4个播期下的籽粒灌浆过程,比较和分析了不同数学模型的拟合效果、部分灌浆特征参数及其计算方法,以期为小麦籽粒灌浆模型选择提供参考。
1 材料与方法
1.1 试验材料与设计
试验于2020年9月-2021年6月在山西农业大学棉花研究所水头农场进行,试验所在地山西省运城市夏县(11°12'E,34°24'N)属黄淮冬麦区,年均气温12.6 ℃左右,年均降水量498 mm,无霜期195 d左右。前茬作物为小麦,土壤为壤土,0~20 cm有机质含量为12.27 g·kg-1,全氮含量为0.85 g·kg-1,速效磷含量为12.6 mg·kg-1,速效钾含量为185.5 mg·kg-1。试验采用裂区设计,播期为主区,设10月12日(SD1)、10月20日(SD2)、10月28日(SD3)、11月5日(SD4)4个播期;品种为副区,供试小麦品种为黄淮冬麦区4个不同类型小麦品种,分别是多穗强筋型品种济麦44、多穗中筋型小麦品种品育8012、大穗强筋型品种周麦36、大穗中筋型品种晋麦84。重复3次,小区面积14 m2,行距 25 cm。4个播期的播量分别为255万、330万、405万和480万株·hm-2,管理与一般大田 相同。
1.2 测定项目与方法
在小麦开花期每小区选择开花一致、长相、长势、大小基本相同的200穗子,进行挂牌标记,花后7 d开始取样,以后每5 d取样1次,直至完熟。每小区取20穗,105 ℃杀青20 min,80 ℃烘干至恒重,脱粒后称籽粒干重,并计算千粒重。
1.3 籽粒灌浆过程拟合模型
1.3.1 三次多项式(Cubic)模型
Cubic方程的数学表达式为:
y=b0+b1t+b2t2+b3t3
(1)
式中,y为千粒重;t为花后天数,设5月4日t=-1,5月5日t=0,其余日期以此类推(下同);b0、b1、b2、b3分别为模拟方程的参数。
对(1)式求导得灌浆速率方程:
Vt=b1+2b2t+3b3t2
(2)
式中,Vt为灌浆速率[g·(1 000 grains)-1·d-1]。
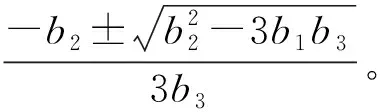


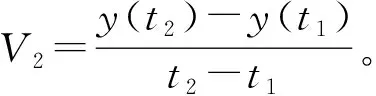
1.3.2 Richards模型
Richards方程的数学表达式:
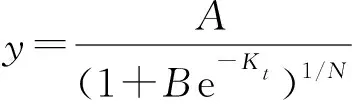
(3)
式中,A、B、K、N分别为模拟方程的参数,A为理论最大粒重。
对(3)式求导得灌浆速率方程:
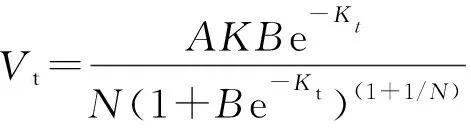
(4)
对公式(3)求二阶导数令其等于零,可得灌浆速率方程两个拐点的灌浆时间t1、t2值:
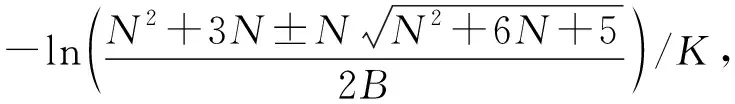
将Tmax代入公式(4)中可求得最大灌浆速率Vmax=AK(1+N)-(1+N)/N
快增期灌浆特征参数T2、V2计算方法同 1.3.1。
1.3.3 Logistic模型
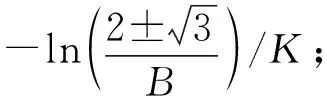
1.4 数据处理
用SPSS 20软件进行籽粒灌浆三种数学模型的方程参数估计,用Microsoft Excel和SPSS 20软件进行灌浆特征参数的计算和数据处理分析,显著性检验采用LSD方法。
2 结果与分析
2.1 三种模型方程参数及拟合度比较
用Logistic、Richards和Cubic三种数学模型对小麦不同品种和播期的灌浆过程进行拟合(表1),各方程决定系数R2均在0.98以上(表2),且均达极显著水平。其中,Cubic和Richards模型的R2显著高于Logistic模型,离回归平方和值显著低于Logistic模型,说明本试验条件下,均可用这三种模型对小麦籽粒灌浆进行拟合,其中Cubic和Richards模型效果较好。

表1 不同播期小麦籽粒灌浆方程Table 1 Grain filling equations of wheat under different sowing dates
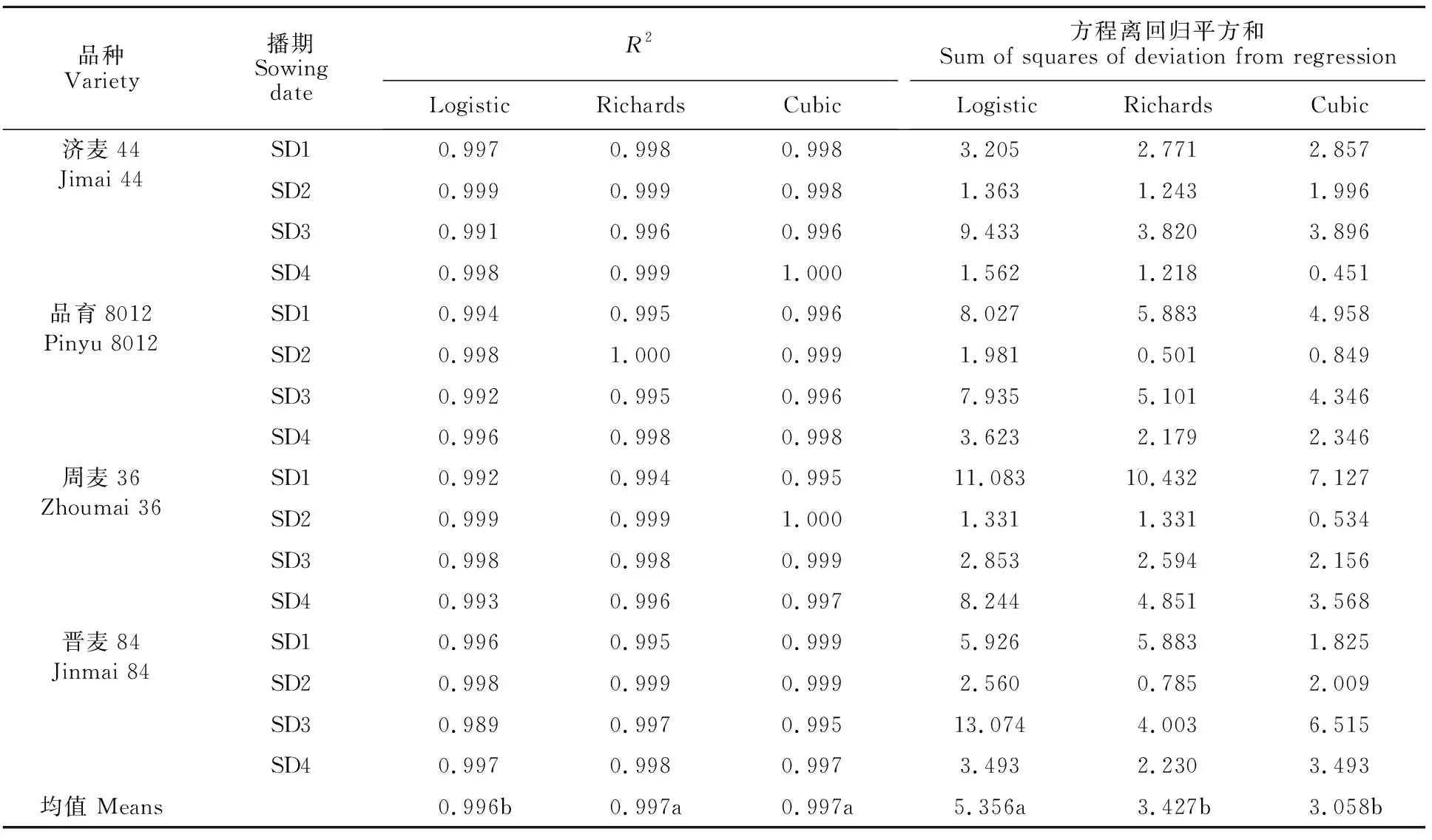
表2 三种模型方程拟合度比较Table 2 Comparison of fitting degree of the three models
2.2 三种模型灌浆起始粒重与起始期分析
Cubic模型可模拟出灌浆起始期,但模拟值较田间观测值晚0.58~6.65 d,除品育8012外,其余三个品种第一播期(SD1)起始灌浆日期模拟值与观测值最接近,周麦36和晋麦84第一播期的模拟值与观测值差值在1 d以内(表3)。
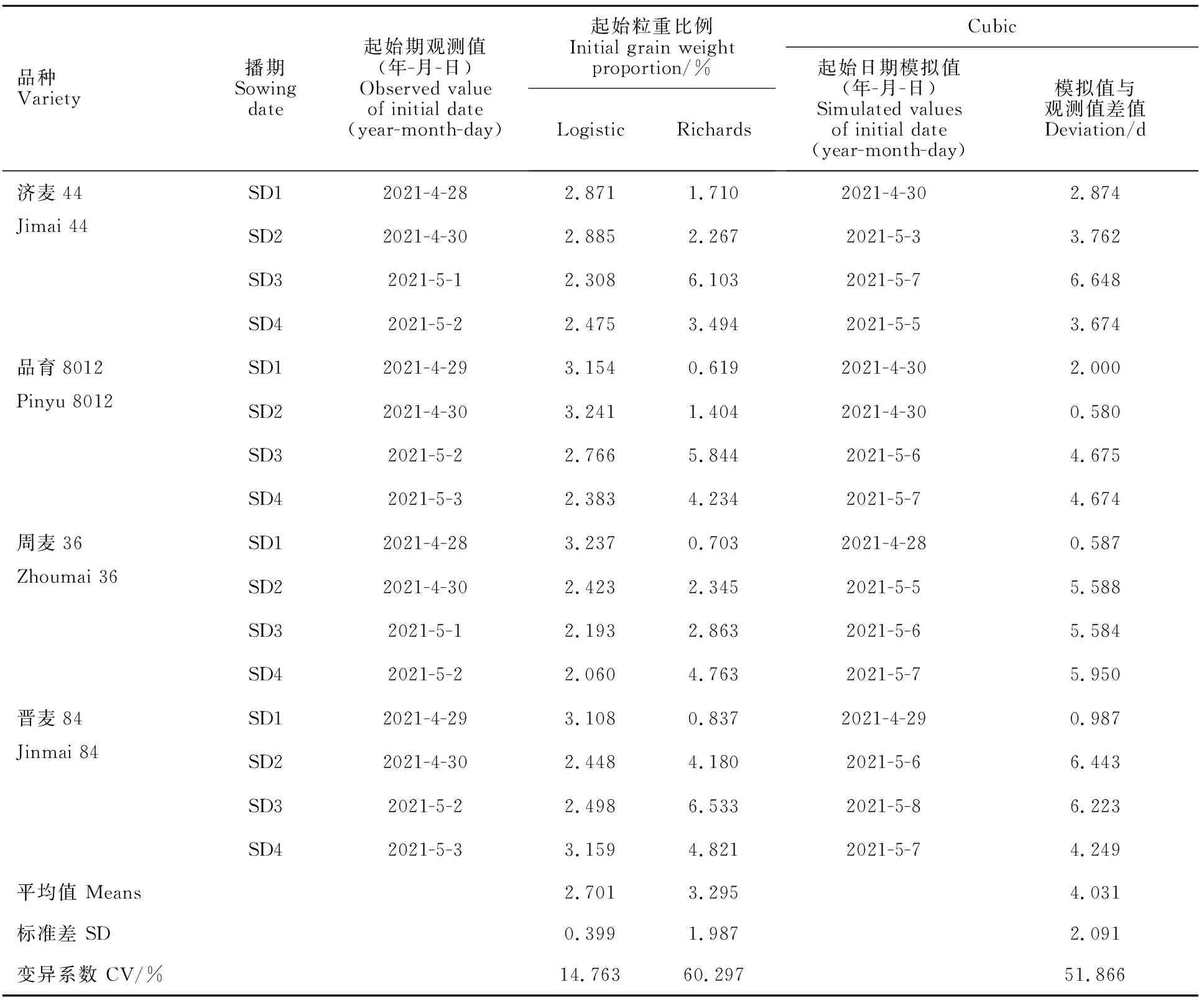
表3 三种模型灌浆起始期模拟Table 3 Simulation of initial grain filling date in the three models
Logistic与Richards模型不能直接计算出灌浆起始期,可通过假定灌浆起始期(开花期)时粒重达理论最大粒重的比例(简称起始粒重比例)来确定灌浆起始日期。Logistic模型中不同品种和播期对起始粒重比例影响不显著,且标准差和变异系数较小,故本试验条件下假定起始粒重比例为其均值2.70%。Richards模型中播期对起始粒重比例有显著影响,4个播期起始粒重比例均值分别为0.97%、2.55%、5.34%和4.33%,第一、第二播期(SD1和SD2)显著低于第三、第四播期(SD3和SD4)。
2.3 三种模型理论最大粒重与灌浆终止粒重 比较
因最后一次取样时小麦籽粒变硬且含水量低于12%,小麦已到完熟期,所以用最后一次取样所测千粒重代表灌浆终止粒重。三种模型理论最大粒重在品种和播期间规律与灌浆终止粒重基本一致(表4)。同一播期下,周麦36和晋麦84粒重高于济麦44和品育8012。随着播期的推迟,济麦44和品育8012的粒重呈降低趋势,晋麦84的粒重先降后升,第三播期粒重最低;周麦36第四播期粒重最低。除晋麦44的Logistic和Cubic模型外,三种模型的理论最大粒重在播期间变异系数大于灌浆终止粒重;Richards模型理论最大粒重的变异系数大于Logistic和Cubic模型。
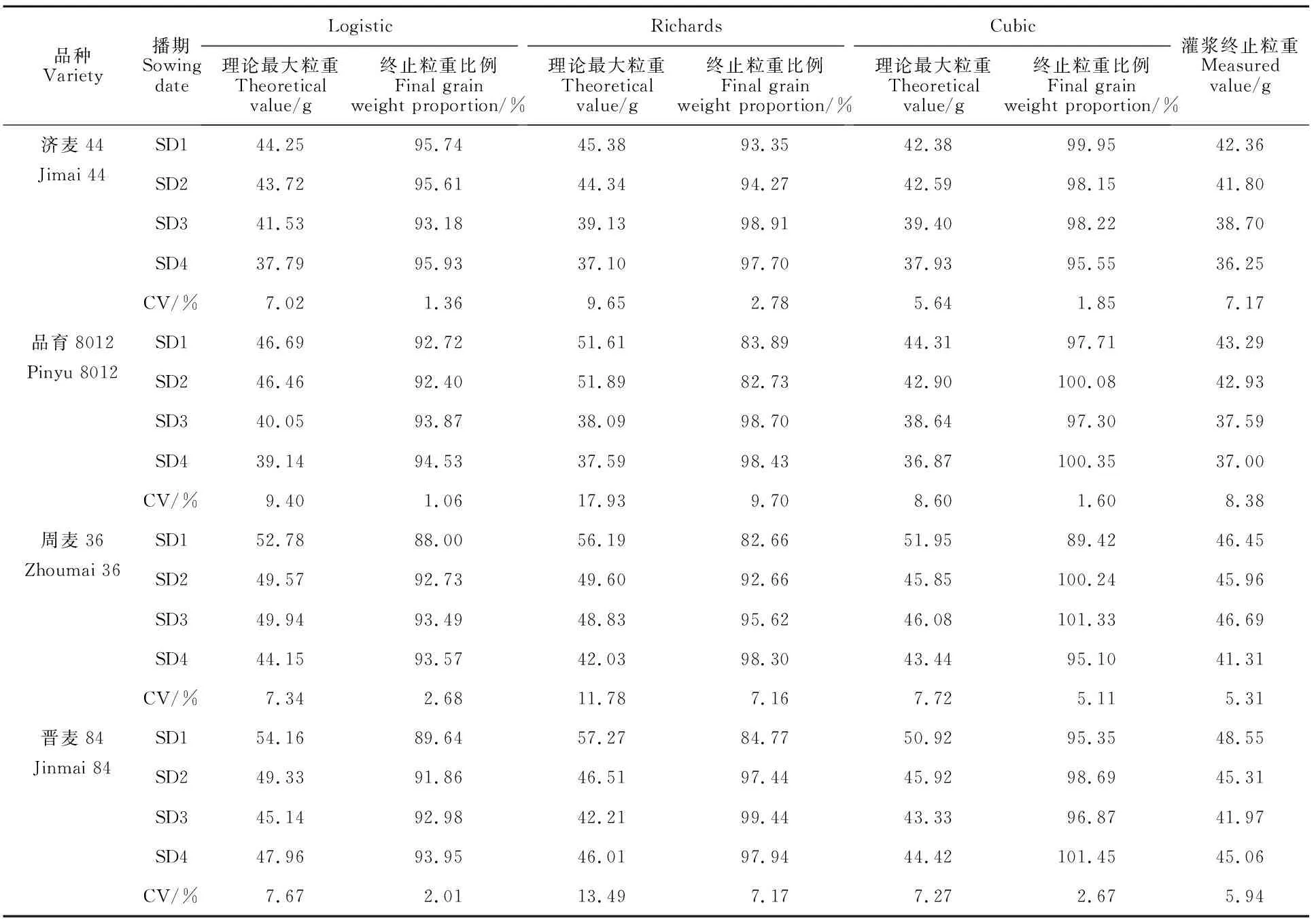
表4 三种模型理论最大粒重与灌浆终止粒重比较Table 4 Comparison between the theoretical highest value and measured value of the thousand-grain weight
Cubic模型理论最大粒重与灌浆终止粒重最接近,终止粒重比例(灌浆终止粒重/理论最大粒重)平均值达97.86%,显著高于Logistic 和Richards模型。Cubic模型中终止粒重比例不同品种和播期间差异均不显著;Richard模型中不同品种的终止粒重比例差异不显著;Logistic模型中,济麦44和品育8012的终止粒重比例大于周麦36和晋麦84;Logistic与Richards模型中,终止粒重比例随着播期的推迟基本呈增加趋势;同一品种下,Richards模型终止粒重比例播期间变异系数大于Logistic和Cubic模型,说明Richards模型终止粒重比例受播期影响的波动最大。
2.4 三种模型籽粒灌浆快增期特征参数比较
三种模型的快增期持续时间(T2)存在差异(表5),且第一、第二播期下表现为Cubic>Richards>Logistic,第三、第四播期下表现为Cubic>Logistic>Richards;三种模型T2、Tmax在品种和播期间规律基本一致,不同品种的T2无显著性差异。同一播期下,Tmax基本表现为:济麦44最最早,其次为品育8012,周麦36和晋麦84最迟;同一品种下,T2表现为第一、第二播期较第三、第四播期长,Tmax表现为第一、第二播期早于第三、第四播期;Richards模型T2和Tmax在播期间变异系数最大,平均值分别为35.25%和20.43%,Logistic模型T2和Tmax在播期间变异系数最小,平均值分别为8.79%和7.59%。
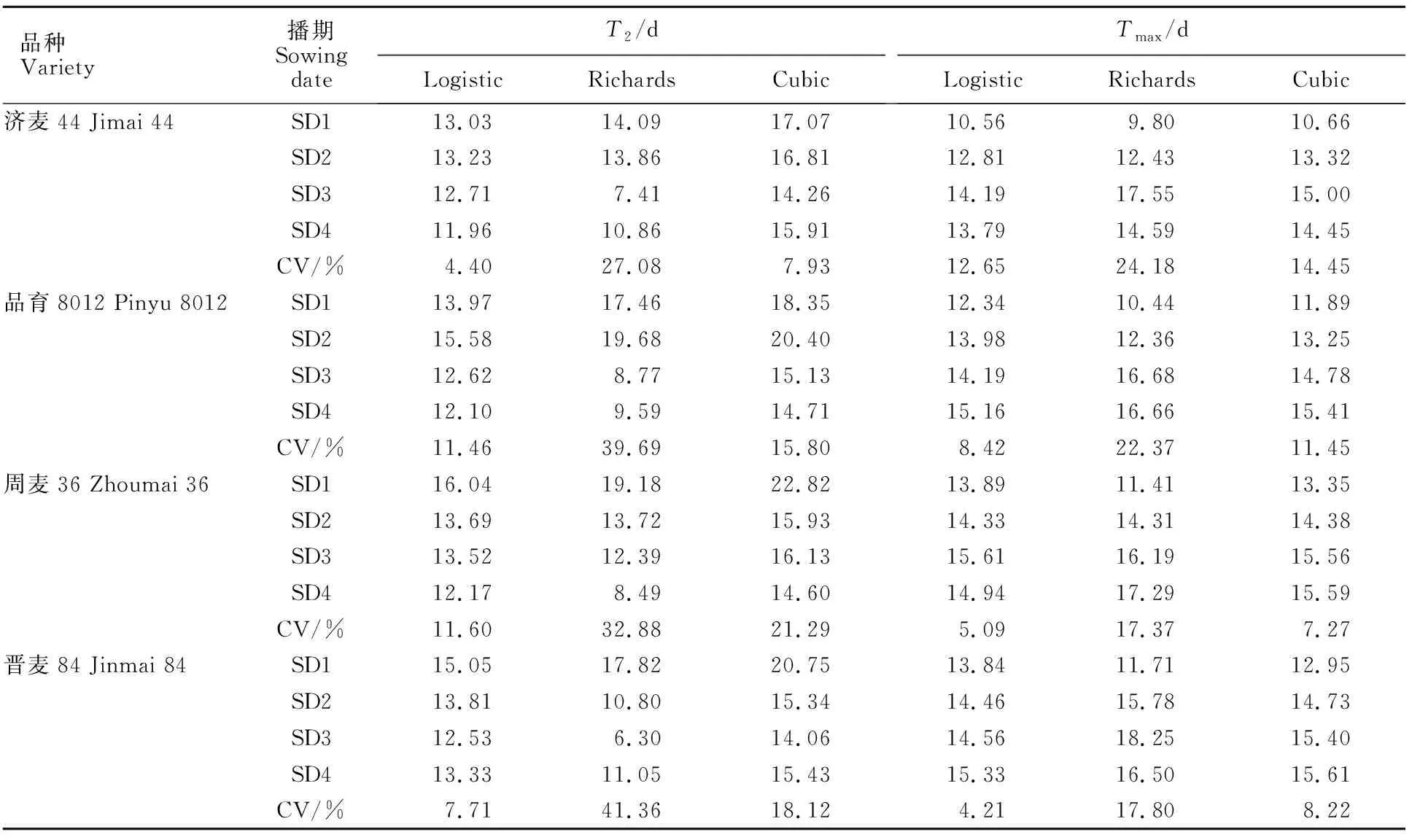
表5 三种模型快增期特征参数T2、Tmax的比较Table 5 Comparison of T2 and Tmax of the three models in rapid growth period
由表6可知,三种模型快增期平均灌浆速率(V2)、最大灌浆速率(Vmax)均有差异,第一、第二播期下基本表现为Logistic>Richards>Cubic,第三、第四播期下基本表现为Richards>Logistic>Cubic。三种模型快增期灌浆速率参数在品种间规律表现一致:第一播期下V2、Vmax均表现为晋麦84>济麦44>品育8012>周麦36,其余播期下,V2、Vmax基本表现为晋麦84和周麦36高于济麦44和品育8012;不同品种和模型V2、Vmax在播期间的规律不一致,济麦44和品育8012在Logistic和Cubic模型中表现为第一播期最大,Richards模型中表现为第三播期最大,周麦36和晋麦84在三模型中V2、Vmax表现为第三或第四播期最大;Richards模型V2、Vmax在播期间变异系数最大,平均值分别为11.94%和10.80%,Logistic模型在播期间变异系数最小,平均值相同为3.30%。
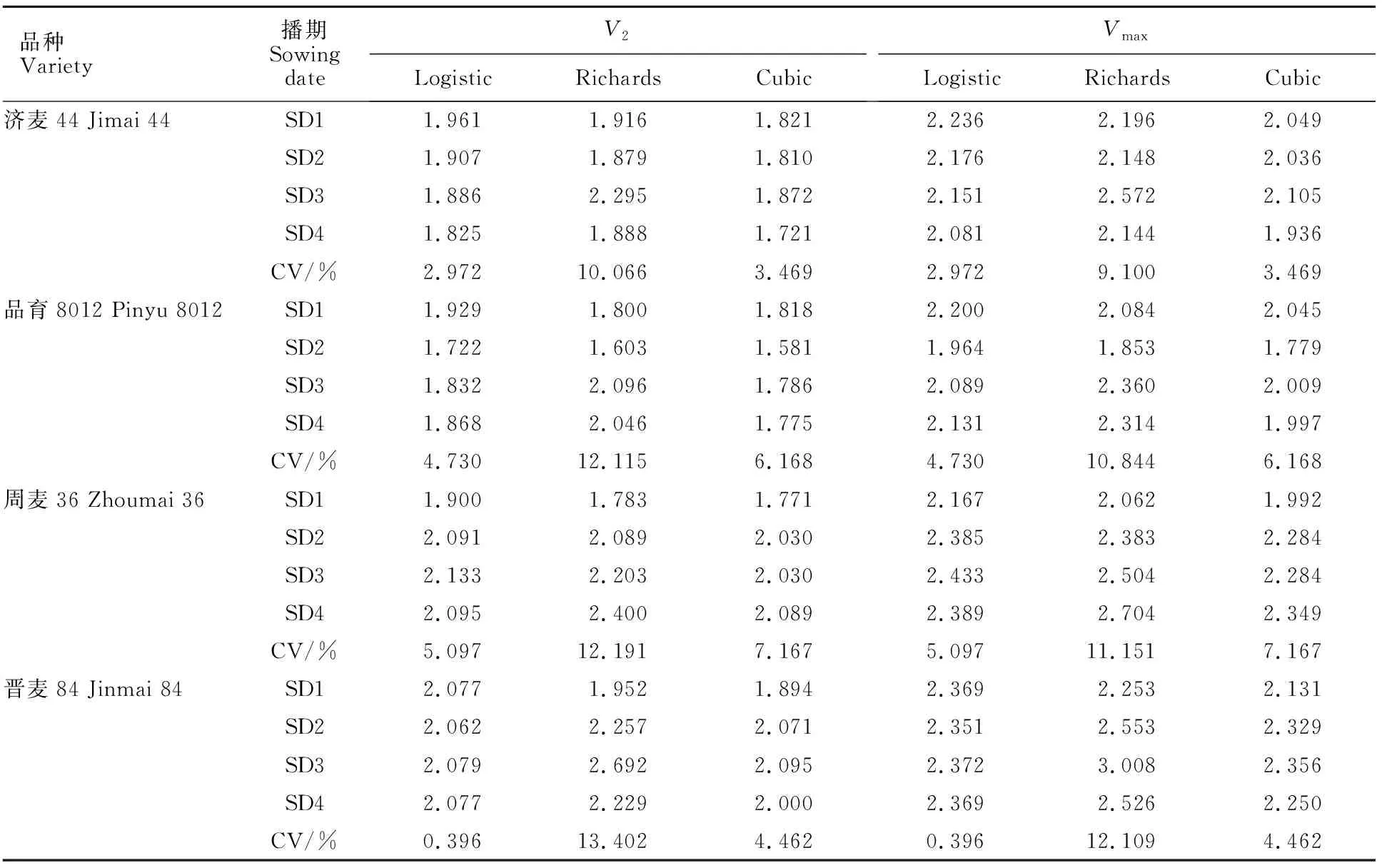
表6 三种模型快增期特征参数V2、Vmax比较
综上所述,三种模型得到的小麦快增期灌浆参数结果有所不同,且Richards模型在播期间差异最大,Logistic模型差异最小。
3 讨 论
3.1 模型中籽粒灌浆起始期和终止期的确定
小麦籽粒灌浆过程呈“慢-快-慢”的“S”型增长趋势,可划分为渐增期、快增期和缓增期3个阶段[23-24]。由于Logistic和Cubic方程曲线具有中心对称性,从这两种方程曲线本身的性质来看,渐增期和缓增期在持续时间和干物质积累量上是一致的,进而计算出的渐增期和缓增期平均灌浆速度也应是相同的;Richards方程虽然可以通过参数N决定着曲线的形状以及拐点的位置,但也不能直接计算出灌浆起始期和终止期。所以灌浆起始期和终止期的确定方法及其准确性是影响渐增期和缓增期灌浆特征参数值的关键因素。由于不同品种及不同播期下小麦开花期不同,且一个麦穗从开始开花至结束一般有3~4 d,同一块麦田开花期持续5~7 d,所以在开花期的观测工作量大且经验性强。Cubic方程可以计算出灌浆起始日期,但本研究表明,通过Cubic模型计算出的灌浆起始期较观测值晚0.58~6.65 d,除SD1(10月12日)播期外,其他三个播期的灌浆起始期模拟值与观测值差异较大。Logistic和Richards模型一般需通过田间观测的小麦开花期确定方程曲线的横坐标,本研究假设开花期为灌浆起始期,拟通过规定籽粒干物质积累达理论最大粒重一定比例(起始粒重比例)时为灌浆起始日期,结果表明在本试验条件下,Richards模型中播期对起始粒重比例影响较大,故不能规定固定的起始灌浆比例,Logistic模型可规定起始粒重比例为2.76%左右,这种方法的可行性还需进一步探索。对于灌浆终止期的确定,Cubic模型灌浆终止期可根据参数计算得出,Logistic和Richards模型一般规定达理论最大粒重的98%~99%时为灌浆终止期[6,17,18],本研究通过最后一次取样值计算的出的终止粒重比例以Cubic模型最大(97.84%),其次是Richards模型(93.55%),最后是Logistic模型(93.14%),且不同品种和播期间差异较大,所以Logistic和Richards模型用98%~99%的固定终止粒重比例来确定不同播期小麦灌浆终止期这一方法有待改进。本研究采用花后7 d开始取样,以后每5 d取样一次的取样方法,第一次取样的时间、取样间隔的天数以及终止取样的时间是否对不同品种和播期处理的方程参数有影响还有待进一步研究。
3.2 品种和播期对籽粒灌浆的影响
基因型是影响小麦籽粒灌浆的主要因素,不同小麦品种的籽粒灌浆特性存在差异[25-26]。有研究表明,灌浆速率与千粒重呈显著正相关,灌浆速率是千粒重的主要决定性因素,而灌浆持续时间并不是千粒重形成的主要决定因素[6,27];也有研究认为,灌浆持续时间对粒重有重要作用[27,29]。研究发现,两种筋型小麦的有效灌浆持续期与千粒重的相关性不同[30];多穗型小麦品种达到最大灌浆速率用时最短,平均灌浆速率最小,理论粒重最轻,中穗型品种整个灌浆期、快增期和缓增期的平均灌浆速率最高,大穗型品种渐增期及灌浆有效期最长,灌浆速率较高[31]。因快增期灌浆特征参数值完全是通过方程参数计算得出的,不涉及观测和估算的数据,故本研究用快增期灌浆特征参数体现小麦灌浆过程的特性,结果也表明,快增期灌浆速率和最大灌浆速率在第二、第三、第四播期下表现为高粒重品种高于低粒重品种,最大灌浆速率出现时间表现为多穗型品种早于大穗型 品种。
播期造成小麦生长发育的环境因素差异。晚播不利于小麦叶片光合性能和籽粒灌浆进程,导致千粒重下降[19,21,32]。在我国北方温带小麦栽培区,籽粒灌浆过程的适宜温度为20~24 ℃,高于25 ℃的温度会缩短灌浆时间,使茎叶早衰,降低籽粒干物质累积量,影响粒重增长[33],迟播会缩短小麦籽粒灌浆的有利时期,增加对灌浆不利的后期高温时期[32]。本试验中,灌浆起始和最大灌浆速率出现时间随着播期的推迟均有所延后,这可能加重了后期高温对籽粒灌浆的不利影响,最终导致灌浆终止粒重随播期推迟呈降低趋势。播期对各灌浆特征参数的影响较大。研究表明,随着播期的推迟,灌浆高峰期有所提前,快增期和渐增期的持续时间明显减少[34];优质强筋小麦品种最大灌浆速率和平均灌浆速率随着播期的推迟而升高,而灌浆持续期随播期推迟反而呈下降趋势[19]。本研究中,随着播期的推迟,快增期灌浆持续时间呈缩短趋势,与上述研究结果相似。在山西临汾,随播期的推迟,优质小麦最高粒重提高,灌浆持续期和有效灌浆持续期延长[30],这与本研究结果不一致,原因可能与播期设置的范围不同,以及本试验设计为晚播增密,降低了晚播后穗数下降的补偿效应有关。赵莉[21]研究得出,小麦籽粒灌浆前期、中期的籽粒灌浆速率随播种期的推迟而不断下降,灌浆后期籽粒灌浆速率随播种期的推迟有所增加。阴卫军[35]认为,不同播期不同品种籽粒的平均灌浆速率存在极显著差异,强筋品种以晚播处理最高,弱筋品种以早播处理最高。本研究表明,不同品种和模型快增期灌浆速率和最大灌浆速率随播期变化的规律不一致,且三模型中Richards模型播期间差异最大,观察Richards模型方程的参数发现不同播期的参数B和N值可以相差几十倍以上,且在第三、第四播期方程中,参数B值出现高达几千至几百万的数值,这对灌浆特征参数的影响还需进一步研究。
4 结 论
虽然用Logistic模型模拟不同品种和播期下小麦籽粒灌浆过程的效果不如Cubic和Richards模型,但其方程的决定系数均在0.98以上,且均达极显著水平,在灌浆起始期不确定的情况下,可以假定粒重达理论最大粒重的2.76%左右时为灌浆起始期。Cubic模型模拟适播期小麦的灌浆起始期比较准确,但在晚播条件下灌浆起始期模拟值与实际值差距较大,Cubic模型的理论最大粒重最能反映灌浆终止时的真实粒重。Richard模型对于播期比较敏感,适于在灌浆起始期和终止期观测比较准确的条件下应用。

