基于模型补偿的机械臂位置跟踪控制研究

钟 辉，袁邦颐，，丁度坤，3，辛曼玉，邓建新，黄秋林，

（1.广东汇兴精工智造股份有限公司，广东 东莞523819;2.广西大学 广西制造系统与先进制造技术重点实验室，广西 南宁 530003；3.东莞职业技术学院 电子信息学院，广东 东莞 523808）

0 引言

当前机器人在各行各业中均大放异彩，在工业生产过程中，为了在整个过程中实现不同任务下的高效率自动化生产，不同自由度的机械臂在不同生产场景下均有其应用。二关节机械臂以其结构简单、成本低廉、控制方便等优点被广泛用于搬运、抓取等作业中[1]，在第二杆后增加一个旋转和平移关节后就形成了常见的Scara机器人，可实现抓取、分拣等功能，如图1所示。

图1 分拣机器人

随着工作任务需求的不断提高，如精密装配、打磨加工等场景，对机器人位置和路径跟踪精度要求也越来越高。控制器的跟踪性能是影响机械臂位置跟踪精度的主要因素，所以，如何设计一个反应迅速和跟踪精确的控制器显得尤为重要。文献[2]针对二连杆机械臂的运动控制问题提出了一种基于深度强化学习的控制方法。文献[3]针对用于三自由度机械臂各关节末端轨迹跟踪控制的非线性系统在扰动存在的情况下跟踪效率较低的问题，提出一种变增益迭代学习控制律。文献[4]提出了一种自适应模糊滑模控制算法。采用自适应单输入单输出模糊系统来计算控制增益。虽然以上方法对不确定模型下的机械臂位置跟踪有较好的效果，但均存在收敛慢、跟踪性能较一般的问题。本研究意在针对模型已知的情况下设计一种控制器，使机械臂能快速准确地跟踪目标轨迹。

1 机械臂控制方法

1.1 PID控制

1936年Callender和Stevenson等给出了比例积分微分（Proportion Integration Differentiation，PID）调节器的算法。此后不断有新的控制算法诞生，但仍无法撼动PID算法在控制领域的地位。当前其已经应用于90%～95%的控制电路中，它具有简单、实用、鲁棒性强等优点[5-7]。在实际应用中，一个简单的线性解耦的PID反馈控制器可以在不引起任何稳态误差的情况下得到期望的位置。

基本的连续PID控制公式如下[6]：

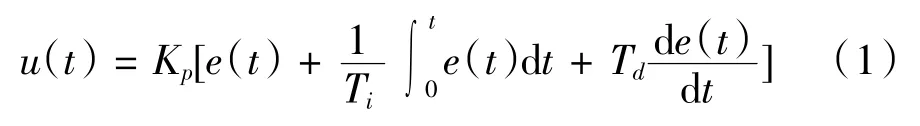
其中Kp为比例系数，Ti为积分时间常数，Td为微分时间常数，e（t）为目标值宇实际值的偏差，t为时间。

其传递函数为：

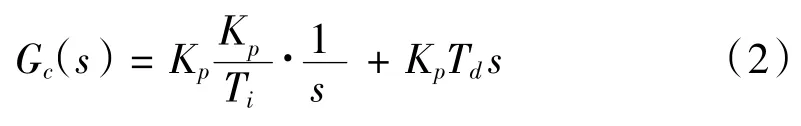
对于PID策略，用户也可取消部分环节如（积分或微分环节）来针对不同系统进行控制，由此衍生出PD、PI等控制算法，各有其优点，不同的控制策略适用于不同的控制系统，调节偏差快速变化时使调解量在最短的时间内得到强化，有调节静差，适合调节滞后环节。例如机械臂的位置跟踪，由于积分环节会在末端收敛时产生震荡现象，导致收敛慢，为达快速收敛的效果，适合使用PD控制器。

1.2 模型偏差补偿与滑模控制SMC简介

对于许多控制系统，因为复杂性或技术问题，常常无法建立精确的模型，但是这会导致控制效果与预期有较大差距，因此对不确定的模型进行适当的补偿具有很大的实际意义[9]，模型偏差补偿是一个思想，通过对误差构成的分析，可以得到一类时变非线性系统的连续轨迹跟踪问题的模型偏差补偿控制方案，可以从仿真的角度得到最好的跟踪效果。

可变结构控制（Variable Structure Control，VSC）与滑模控制（Sliding Mode Control，SMC）已广泛应用于具有不确定性和或输入耦合的系统。其设计理念是获得一个频繁切换控制律，将系统驱动到一个指定的和用户选择的表面上，称为滑动表面。当系统处于滑动模式时，其动力学严格由滑动表面的动力学决定，因此对参数变化和系统扰动不敏感，鲁棒性强，滑模控制另一个优点就是对非线性系统具有良好的控制效果。

机器人作为一个复杂的、时变的、非线性的、具有很多建模不确定性项的系统，单一地PID控已经无法满足其路径跟踪需求，为了提升PID控制的鲁棒性，本研究将传统的比例微分（Proportion Differentiation，PD）控制与模型偏差补偿相结合，设计了基于模型补偿的机械臂PD型控制器。

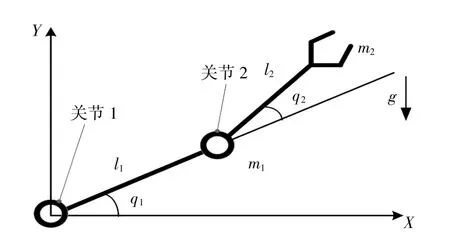
图2 二关节机械臂模型

2 机械臂模型

忽略关节间的摩擦力和其他干扰力，n关节机械臂的动力学方程为：

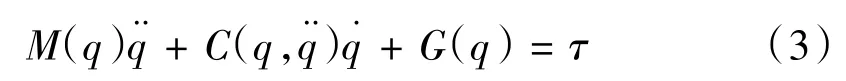
其中q为n×1的关节位置向量，M（q）为n×n的机械臂惯性矩阵，C（q，）为n×n的离心力与科氏力结合矩阵，G（q）为n×1的重力矩阵，τ为各关节电机输出的力矩。

机械臂系统动力学有以下特性：（q）-2C（q，）是一个斜对称矩阵，xT[（q）-2C（q，）]x= 0；惯性矩阵M（q）是对称正定矩阵[11]。

由于机械臂相邻关节间存在耦合，无法用一般方法对其进行动力学建模，当前常用的二关节机械臂动力学模型的构建方法主要有：拉格朗日法（Lagrange）、牛顿-欧拉法（Newton-Euler）、凯恩法（Kane）等方法。其中拉格朗日法利用系统能量的微分求出力和力矩，适用于较为复杂条件下的系统建模。

根据拉格朗日法可获取机器人动力学参数，表示为：

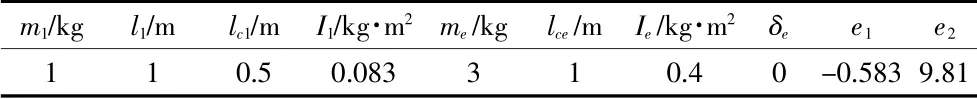
表1 二关节机械臂物理参数表

其中m1为关节1质量，l1为关节一的长度，lc1为关节1质量中心距第一关节长度，I1为关节一的转动惯量，me为质量，lce为质量中心距第二关节距离，δe为质量中心与第二杆之间的夹角。

3 基于模型补偿的PD机械手控制器设计

S函数（S-Function）是一种由用户自定义功能的Simulink模块。利用S-function也可以定义自己的微分方程、差分方程、离散系统方程。当Simulink自带模块不足以满足需求时，我们可以利用S函数来编写所需的功能模块，从而扩展Simulink的功能。

S函数相当于在Matlab中提供了一个模板程序，用户通过修改模板程序，根据需求在各个子函数中编写对应程序，即可自定义S函数模块的功能[10]。

S函数通过flag标志来控制运行顺序，共包含6个子程序，分别是：

①mdlInitializeSizes初始化；

②mdlDerivatives（t，x，u）计算连续状态的微分；

③mdlUpdate（t，x，u）更新离散状态、采样时间与最大步长；

④mdlOutputs（t，x，u）计算S函数输出；

⑤mdlGetTimeOfNextVarHit（t，x，u）计算下一个采样时间；

⑥mdlTerminate（t，x，u）。

根据Lyapunov第二方法来设计控制器，可以定义机械臂位置误差为，其中q=[q1q2]T，q=[q1q2]T。Λ为一个2×2的正的常数比例矩阵，-

设计基于模型补偿的PD型控制律为：

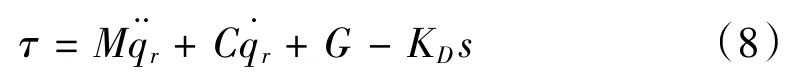
其中KD为正定的微分矩阵。

构造Lyapunov函数：

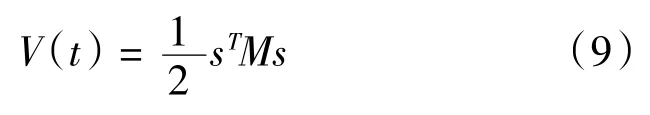
对其求导得：

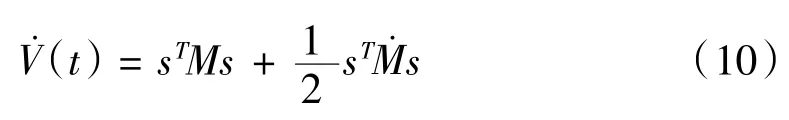
将 式（3）（4）代入上式可得：

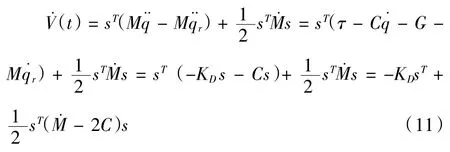
由前文可知：

xT[]x，KD为正定的微分矩阵，则有：

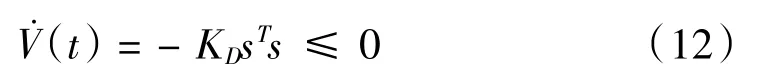
所以V˙（t）为半负定的，当且仅当s=0时，V˙（t）=0，根据LaSalle[11]定理可知系统收敛。

4 基于Matlab/Simulink的仿真

为验证以上控制模型，在Matlab2020b中搭建了控制系统的仿真模型，并同时搭建仅基于PD控制的二关节机械臂位置控制仿真模型作为对照。使二关节机械臂按照期望位置qd=[sin（2πt）sin（2πt）]T进行运动。

经过参数整定后，设计用于对照的基于PD控制的二关节机械臂位置控制器参数为，

能达到较好的控制效果。

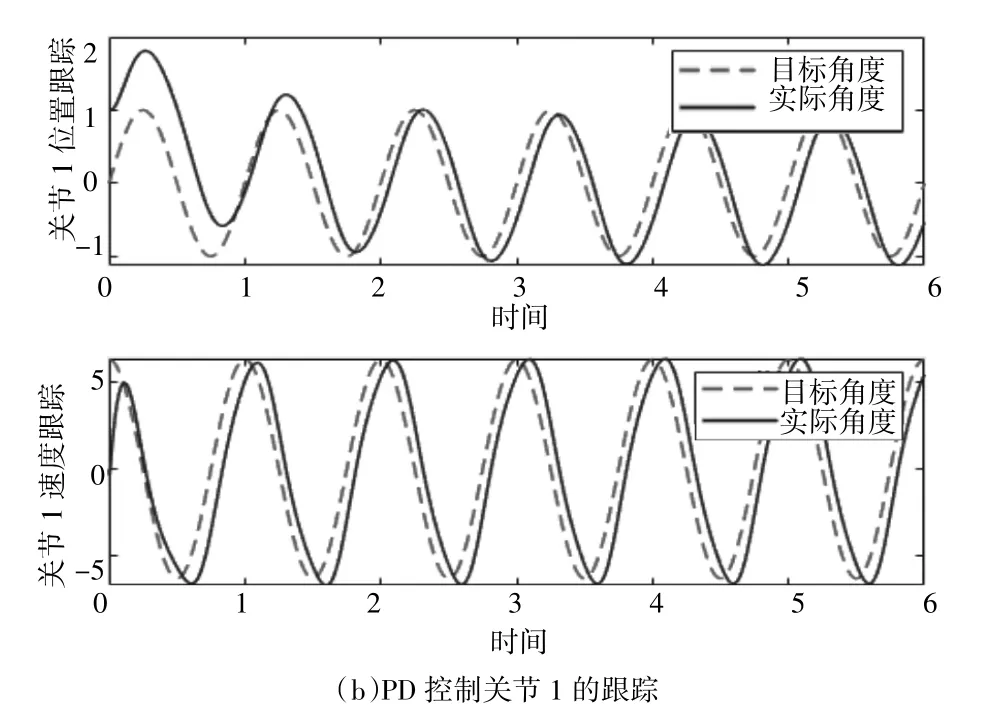
图3 关节1的位置和速度跟踪

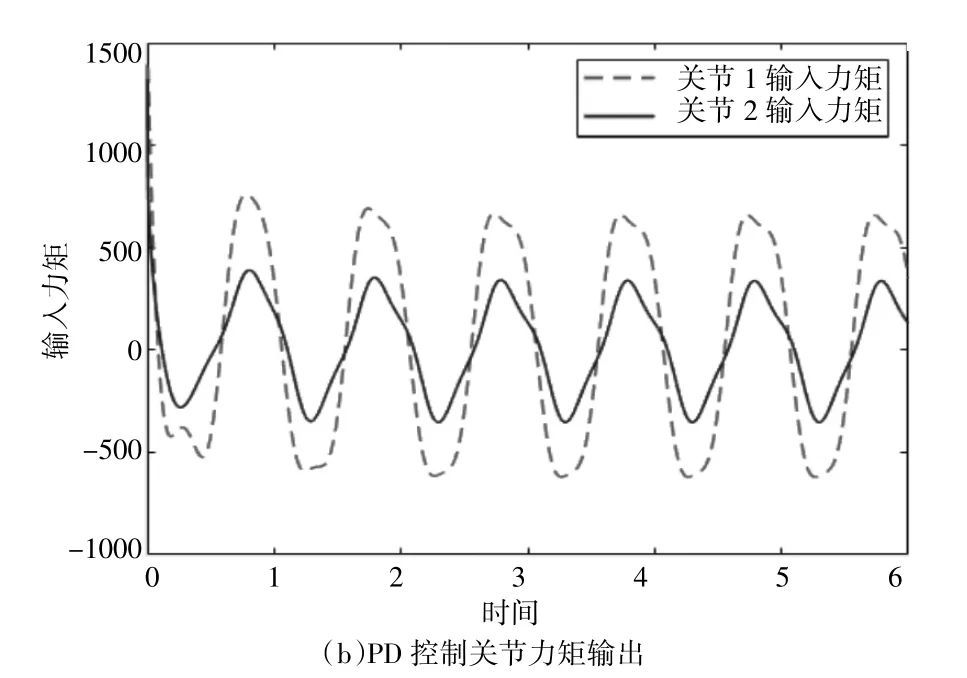
图5 关节力矩输出

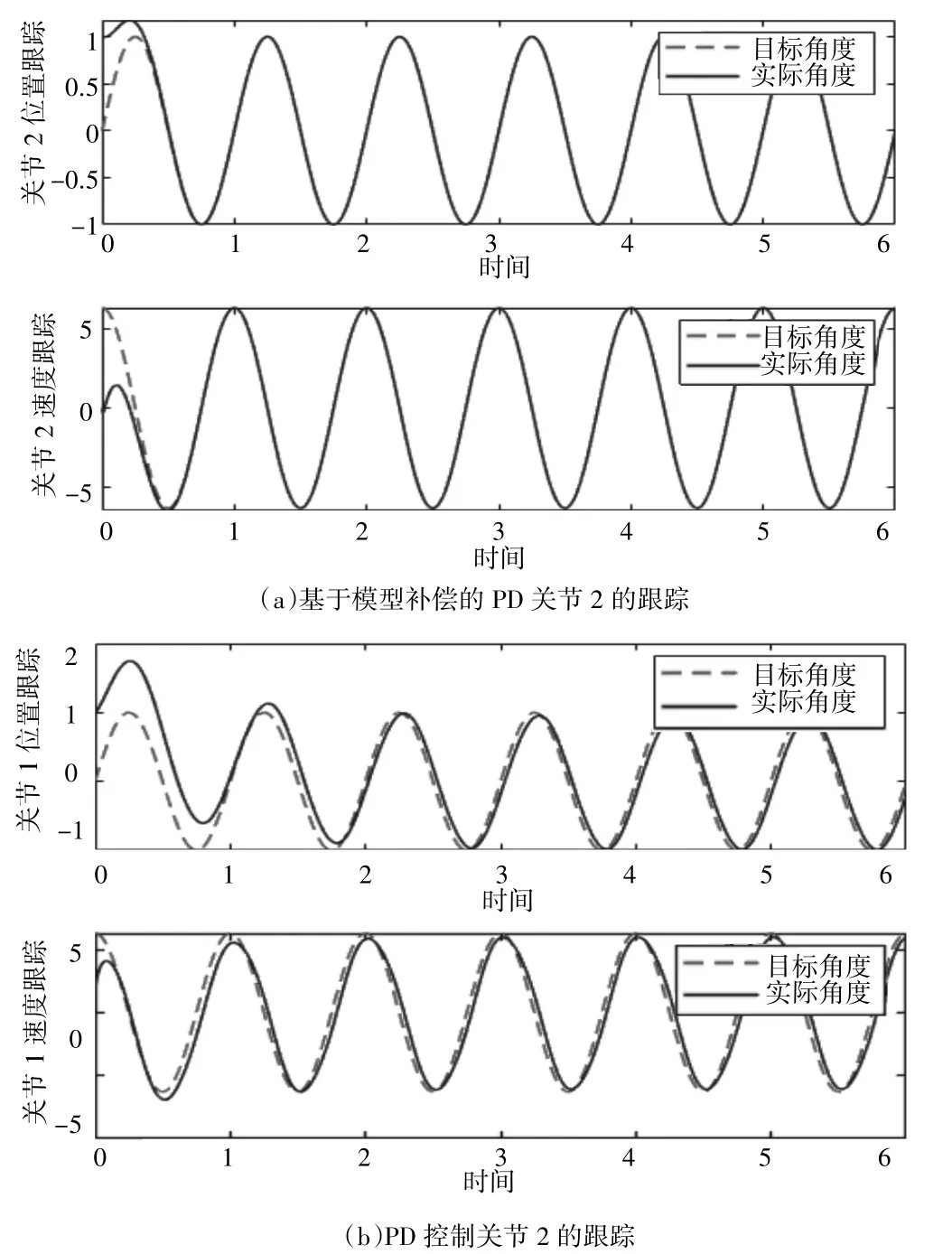
图4 关节2的位置和速度跟踪

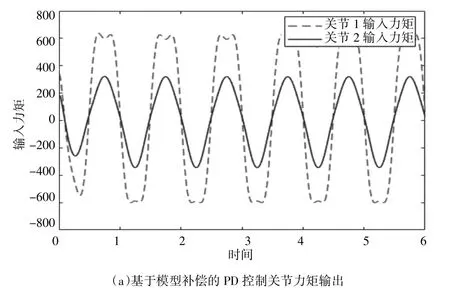
从以上仿真结果可以看出，基于模型补偿的PD型控制方法位置跟踪收敛时间在0.4 s，而传统PD控制则是1.9 s左右，且稳态跟踪误差可以精确到控制到1%以内，而传统PD控制关节1位置跟踪则存在滞后性，关节2位置跟踪误差则达6%。无论是调节时间还是稳态误差，都是所提方法跟踪性能更好。综上，所设计的控制器对两个关节的位置和速度跟踪性能都是令人满意的，这表明控制器能够达到控制要求。

5 结语

通过PD控制与滑模控制相结合设计的基于模型补偿的机械手PD控制器，并在Matlab/simulink中建立仿真模型，采用S函数编写各个模块进行仿真，同时建立传统的机械臂PD位置控制模型，与所设计的控制器进行对比，仿真结果表，该控制器跟踪性能优于传统的PD控制器，能够很好地跟踪预定的关节轨迹。