冷扩管锥体与管件内壁间减摩效果评价与预测*

韩 猛 魏松波 孙 强 魏 然 郭岩宝

(1.中国石油勘探开发研究院 2.中国石油大学(北京))

韩猛,魏松波,孙强,等.冷扩管锥体与管件内壁间减摩效果评价与预测.石油机械,2022,50(11):133-139.

0 引 言

膨胀管技术在石油工程领域主要用于套管加固、层系封堵及井筒重构[1-6]等,其施工过程可等效为无缝金属管在膨胀锥作用下进行冷塑性扩管的过程。扩管膨胀力主要取决于管材塑性变形力和膨胀过程中的摩擦力,所以降低膨胀管摩擦力在膨胀力中的占比对膨胀管安全作业至关重要。

国内外学者对膨胀力及其影响因素开展了一系列研究。陈功剑等[2]研究了管材材料、膨胀速度、膨胀锥表面状态、膨胀率等因素对摩擦力的影响,并建立了膨胀过程的摩擦力学模型,得出摩擦因数大于0.25后会出现明显犁沟现象的结论;王绍先等[3]分析了不同摩擦因数对套管膨胀后的力学性能影响。分析表明摩擦因数越大,壁厚减薄越明显;于洋等探讨了膨胀率、屈服强度、摩擦因数和膨胀锥角对膨胀力的影响;朱海波等[4]利用石墨、双马来酰亚胺、酚醛改性环氧树脂,研制了膨胀管内涂层,该内涂层具有较好的摩擦磨损性能;魏松波等[5]采用超音速火焰喷涂技术在合金钢膨胀锥表面制备了碳化物硬质涂层,并采用锂基酯和水作为润滑剂,使膨胀锥磨损明显减轻;D.DI CRESCENZO等[7]提出了使用加速试验优化润滑剂的方法,该加速试验采用专用装置,模拟膨胀过程中苛刻的井下条件,对3种润滑剂和1种专为管式膨胀应用开发的新型固体润滑剂进行了测试,试验的重点是钻井液和温度对摩擦、磨损和润滑效率的影响;武刚等[8]通过有限元仿真分析认为,对膨胀力的影响因素从大到小为膨胀率、摩擦因数、屈服强度、膨胀锥角;王全宾等[9]分析了不同材料对膨胀管膨胀后径向变形、轴向变形和环向残余应力的影响;白强等[10]基于实体膨胀管评价试验平台,对比分析了膨胀后力学性能、金相组织、抗挤强度变化,发现膨胀后膨胀管力学性能显著变化而金相组织无变化;白强等[11]利用金属塑性变形理论,用解析法给出了ø139.7 mm×7.72 mm的N80膨胀管以15%膨胀率膨胀时所需的膨胀力;尹虎等[12]利用弹塑性力学分析方法计算了膨胀管塑性极限的最小膨胀力;梁坤等[13]根据有限元理论分析了膨胀力影响因素,认为膨胀力随摩擦因数的增大而增大,随膨胀锥角先变小后变大。

综上可知,现有研究仅针对膨胀管摩擦力进行定性分析与理论计算,对于指导工程设计,得出实际的可参考的结果方面仍有欠缺;而且以实际尺寸开展膨胀管膨胀过程中冷挤压塑性变形减摩效果,存在所需试验设备庞大、操作复杂和成本较高等问题。为此,笔者通过采用ø41.5 mm×3.5 mm规格的试验管件,设计3种减摩方案开展冷挤压塑性变形减摩效果试验,并建立模型,仿真模拟膨胀力和摩擦因数的关系,计算了摩擦力在膨胀力中的占比,以此作为主要评价标准;模拟了3种方案下实际尺寸管件应力、轴向收缩量与壁厚减薄量的变化,以期为指导工程设计提供重要参考。

1 室内试验

1.1 试验件规格与性能

试验管件配套扩管用锥体几何尺寸见图1。锥体材料弹性模量为210 GPa,泊松比ε为0.27,屈服强度为288 MPa,切线模量为1 048 MPa。

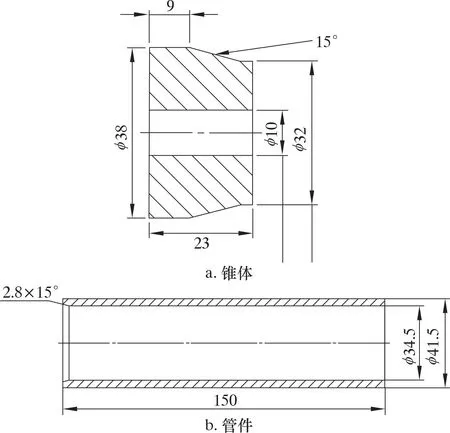
图1 试验用锥体与管件规格图Fig.1 Specifications of test cone and tube

试验管件材料的弹性模量为210 GPa,泊松比为0.27,屈服强度为520 MPa,切线模量为1 229 MPa。

使用实验室拉压试验机进行试验时,其安装方式如图2所示。

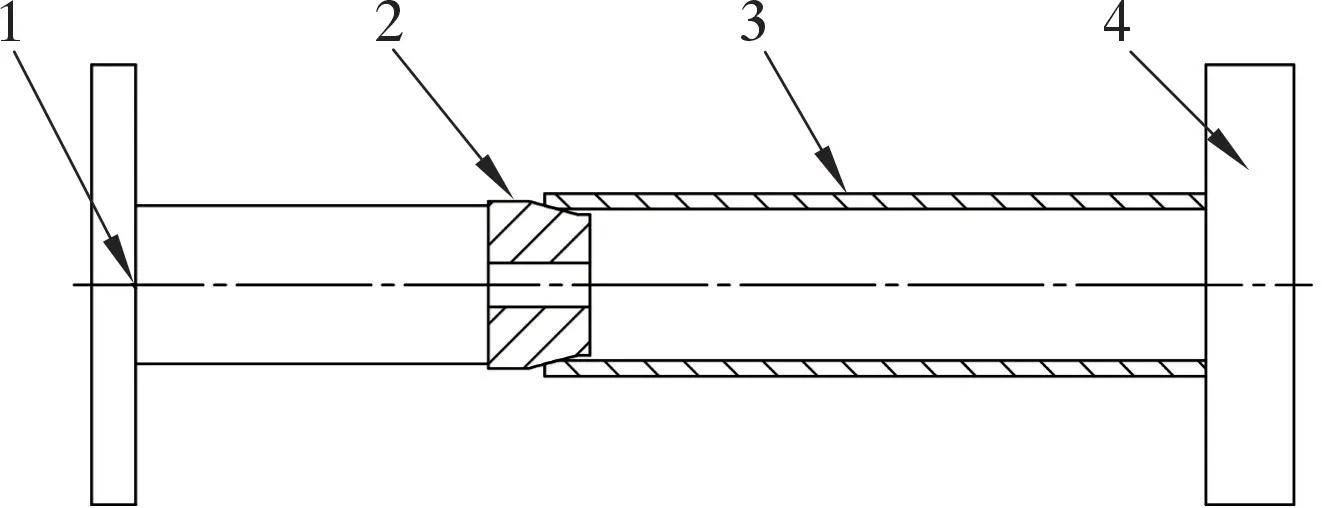
图2 试验件安装与试验状态图Fig.2 Tensile and compression testing machine

1.2 试验步骤与膨胀力

采用3种减摩方案处理试验管件[14],分别定为1#、2#和3#试验方案。试验中设置锥体向下加载速度为10 mm/min,加载距离为60 mm,分别对3种减摩方案处理过的试验管件实施多轮次扩管试验,试验结果具有可重复性。得到3种减摩方案下的膨胀力与位移的关系,如图3所示。

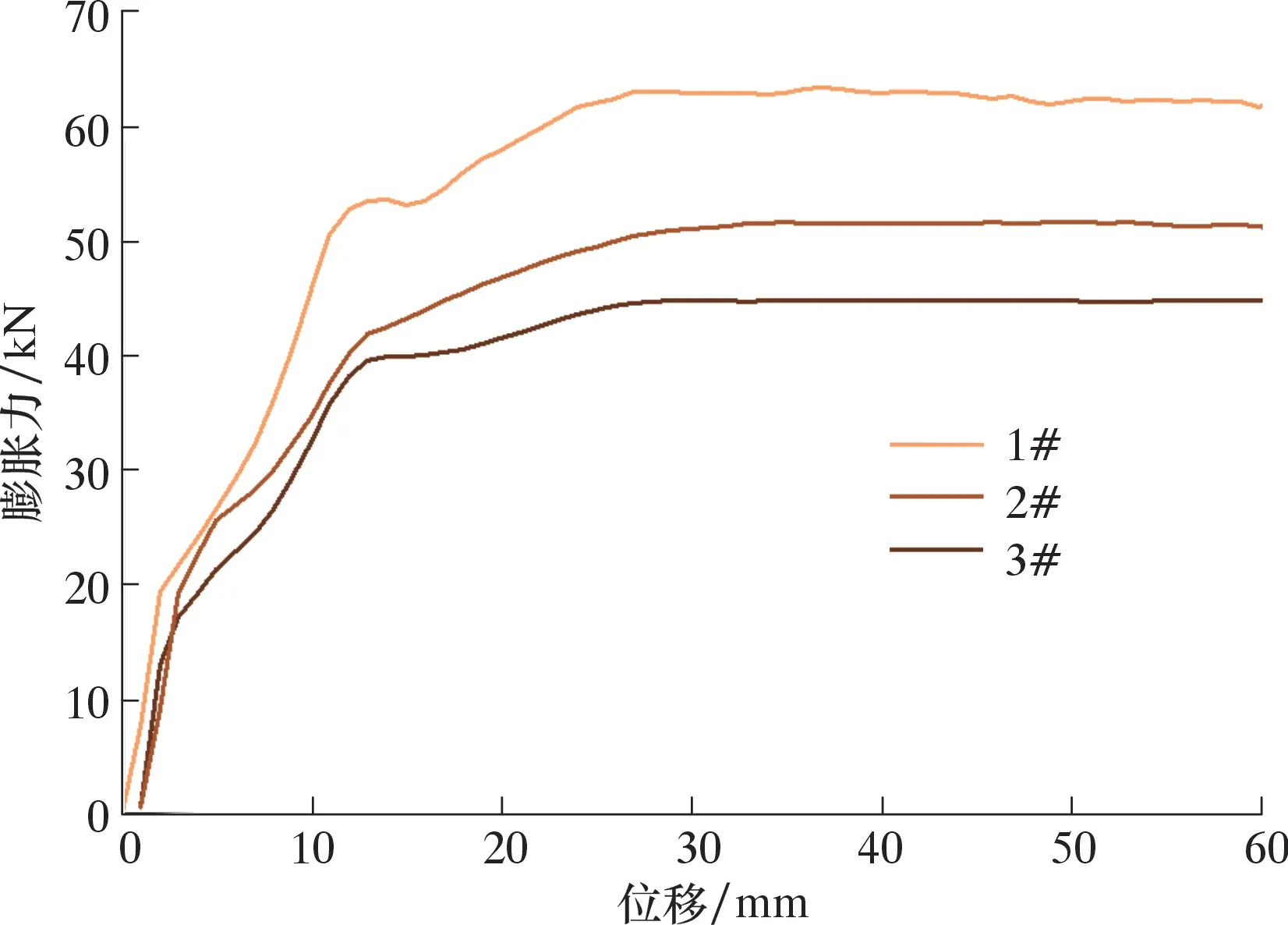
图3 不同减摩方案下膨胀力与位移的关系Fig.3 Relationship between expansion force and displacement in different lubrication schemes

结合试验结果,将试验管膨胀过程分为4个阶段:第1阶段锥体逐渐进入管口,对应曲线第1次转折前,此阶段管口逐渐胀开,但锥体最大径段尚未进入管口,膨胀力快速增大;第2阶段锥体最大径段开始进入管口,此阶段锥体斜面已完全进入管内,但锥体尾部尚未完全进入管内,膨胀力仍快速增大;第3段锥体尾部完全进入管件,管口出现缩口,锥体继续进入管件,膨胀力持续增大,主要原因是锥体受缩口影响,膨胀力仍未达到平稳阶段;第4阶段膨胀力稳定,此阶段膨胀力不再由于位移的变化而发生变化。据此,将此4个阶段称为:胀入段、包覆段、待稳段、稳定段。具体区分尺寸如表1所示。

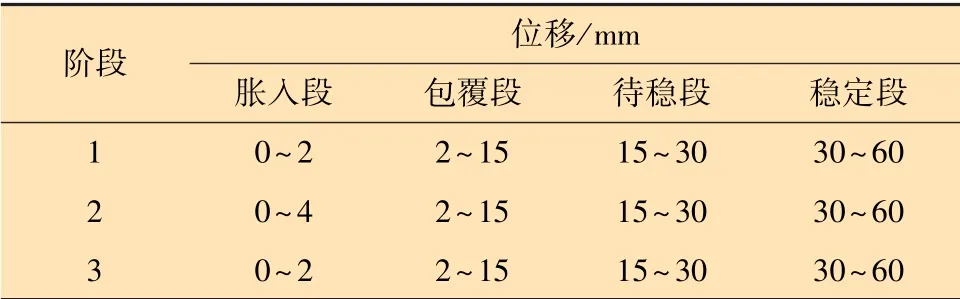
表1 不同减摩方案下四阶段膨胀力位移Table 1 Expansion force displacement in four stages under different lubrication schemes

由图3可知,3种减摩方案稳定段的膨胀力分别为:1#膨胀力为62.49 kN,2#膨胀力为51.50 kN,3#膨胀力为44.73 kN。

2 有限元仿真分析

2.1 模型建立

由于试验管件扩管过程会产生塑性变形,这在有限元分析中为大变形非线性静力学仿真,涉及几何非线性与材料非线性问题,所以在计算过程中需对模型进行简化。利用Solidworks制作回转体2D模型,如图4所示,再将其导入ANSYS Workbench进行静力学分析。

图4 试验管件和膨胀锥简化模型Fig.4 Simplified model of test tube and expansion cone

选择塑性模型为双线性各向同性模型,主要使用弹性模量和切线模量来表示材料弹性和塑性阶段的应力-应变曲线斜率,此模型忽略了温度对膨胀过程的影响。切线模量ET为塑性变形过程中的重要参数,其计算方法为:

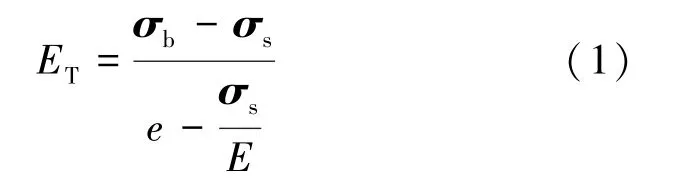
式中:σb为抗拉强度,MPa;σs为屈服强度,MPa;e为伸长率;E为弹性模量,MPa。

2.2 网格划分与约束

加载膨胀过程中,试验管件主要发生径向的塑性变形,管壁径向网格需至少划分3层网格,以描述在塑性变形过程中内、中、外壁金属塑性蠕动情况。网格设置以六面体网格和四面体网格相结合,壁厚中间部分几乎不参与金属塑性成形中的蠕动过程。进行几次试求解后,将网格调整为沿厚度方向八层网格以满足求解收敛条件,如图5所示。

图5 试验管件和锥体网格划分Fig.5 Mesh division of test tube and cone

将拉压机上管件摆放的约束转化为有限元模型中的约束。管件一端放置在试验机平台上,故管件轴向方向位移被约束;锥体仅有轴向位移,从有倒角的一端进入试验管件实施扩管。在Workbench中建立约束,如图6a所示,B处视为试验管件接触试验机平台的一端,设置B处为径向位移约束,不约束轴向位移;A处为锥体大径端,设置轴向位移,以表示锥体进入试验管件。

试验管件内壁与锥体倒角处为摩擦接触,由于此处没有刚体设置,故接触体和目标体不用特意区分;试验管件和锥体接触设置如图6b所示。

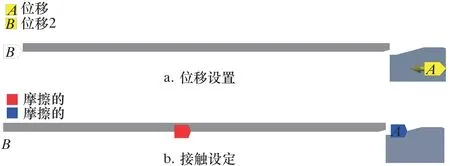
图6 试验管件和锥体位移设置Fig.6 Simulation analysis settings of test tube and cone

2.3 有限元仿真及分析

3种减摩方案试验管件与锥体的实际摩擦因数难以直接测量,故通过有限元仿真获取摩擦因数与膨胀力的关系,将试验获得的膨胀力代入上述关系中,获取近似的摩擦因数。设置摩擦因数μ分别为:0.000 1、0.005 0、0.100 0、0.150 0、0.200 0、0.250 0、0.300 0。

不同摩擦因数下膨胀力仿真曲线如图7所示。

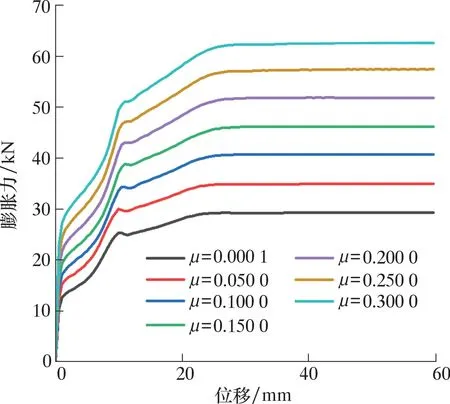
图7 不同摩擦因数下的膨胀力曲线Fig.7 Expansion force curve with different friction coefficients

由图7可知:①膨胀力随锥体位移变化主要分为4个部分,即胀入段、包覆段、待稳段、稳定段,仿真曲线与试验所得曲线具有良好的一致性;②无摩擦的情况并不存在,但可采用仿真计算近似得到无摩擦时的情况,将摩擦因数设置为0.000 1,此时摩擦力可忽略不计,稳定段的膨胀力近似等于试验管件扩管过程的变形力,下文将以此作为评价摩擦力与变形力所占比例的一个重要参数。0.000 1～0.300 0摩擦因数下膨胀力与摩擦因数的关系如图8所示。

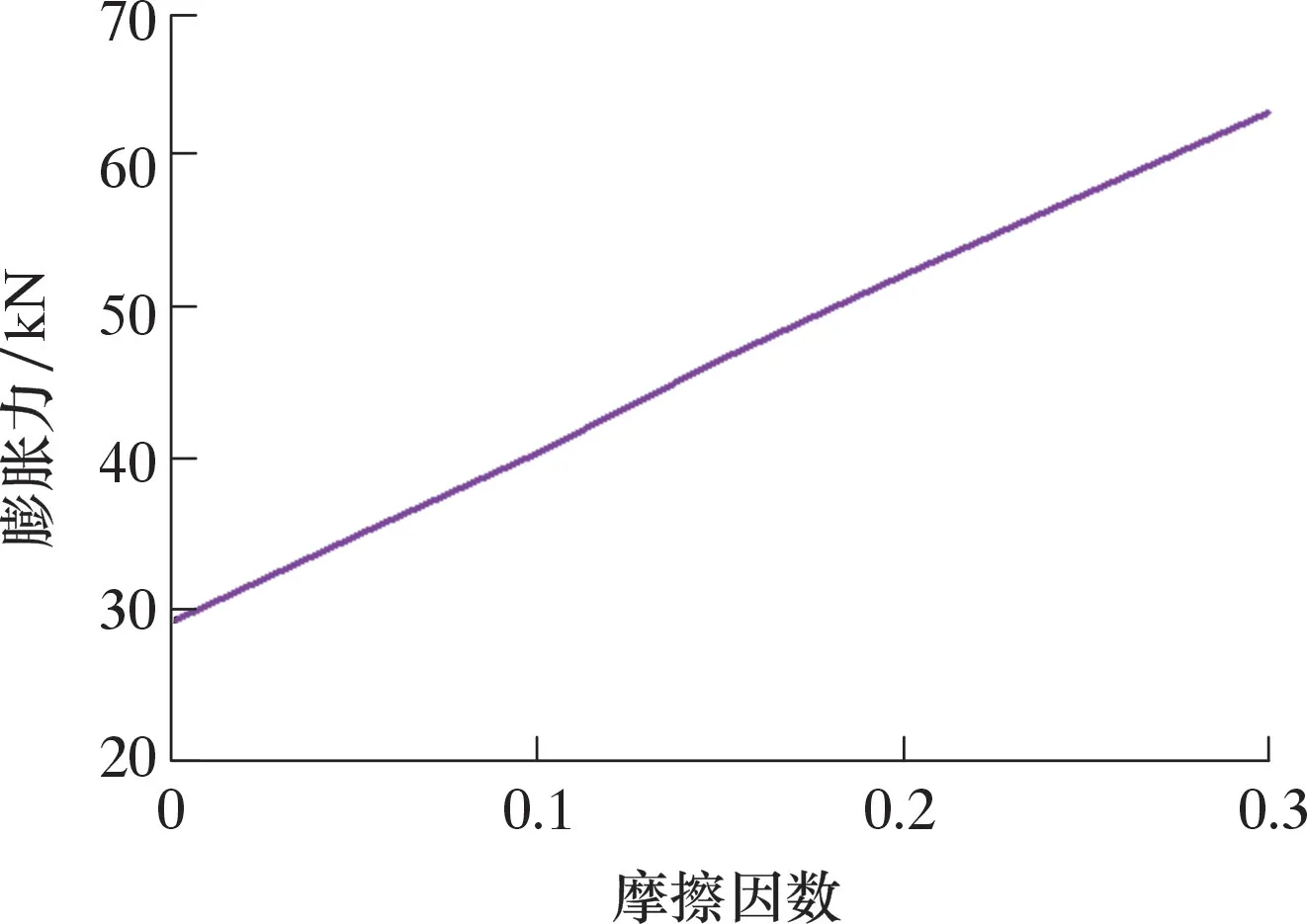
图8 膨胀力与摩擦因数的关系Fig.8 Relationship between expansion force and friction coefficient

3 减摩处理对试验管的影响

3.1 不同方案下摩擦力占比

将拉压试验机所得的膨胀力代入到有限元仿真得到的膨胀力与摩擦因数的F-μ关系式,可得到不同膨胀力对应的近似摩擦因数,如表2所示。摩擦力在膨胀力中的占比由下式可得:

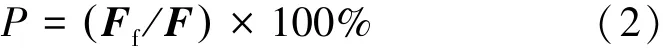
摩擦力、变形力与膨胀力的关系如下:

将式(3)代入式(2)可得:

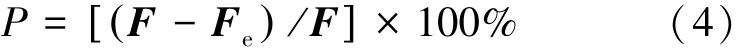
式中:F为膨胀力,kN;Ff为摩擦力,kN;Fe为塑性变形力,kN。

需要说明的是:式(3)在受力分析中没有实际含义,仅代表膨胀力主要受变形力与摩擦力影响。Fe可认为是有限元仿真中摩擦因数为0.000 1情况下的膨胀力,近似结果为29 kN。3种减摩方案下摩擦力占比如表2所示。

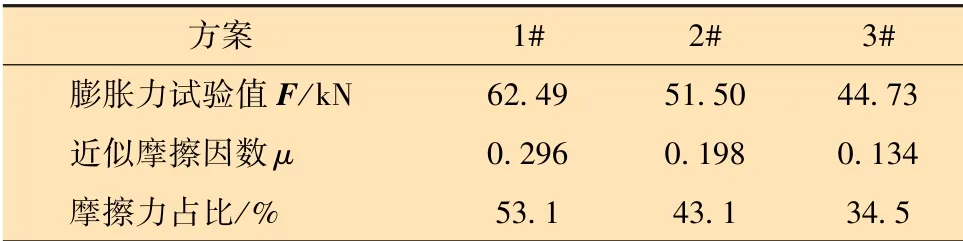
表2 不同减摩方案下摩擦力占比情况Table 2 Friction proportion in different lubrication schemes

3.2 不同方案下von-Mises应力

将摩擦因数代入到有限元仿真中,可得到不同方案下的von-Mises应力如图9所示,其中4#方案为近似无摩擦(摩擦因数为0.000 1)时的应力状态。

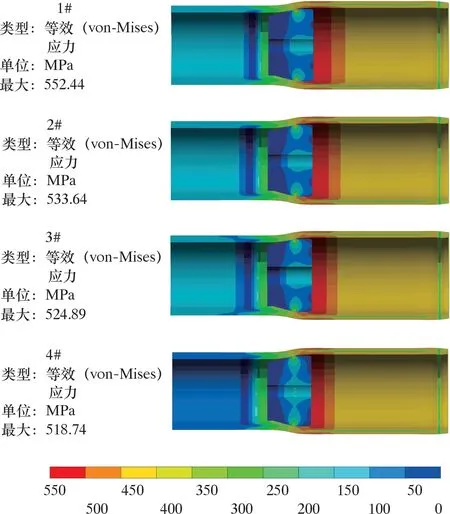
图9 不同方案下试验管件的von-Mises应力Fig.9 von-Mises stress of test tube in different schemes

由图9可以得出:

(1)最大应力出现在试验管件扩管完成后刚刚脱离锥体那一小段的内外壁区域。

(2)管壁中间区域应力较小,主要是由于金属蠕动部位为管材内外壁面,中间为类似中性面的区域;模型进口处出现环状低应力区域,主要原因是锥体进口处存在倒角。

(3)锥体应力集中区域出现在与试验管件接触区域,这为减摩方案的作业区域提供了有效参考。

(4)随着摩擦因数的增大,锥体接触区域应力增大。摩擦因数由0.000 1升至0.296 0时,试验管件胀出区域最大应力由518.74 MPa增大到552.44 MPa。由此可知,随着摩擦力上升扩管过程中管件最大应力也随之增加。

3.3 不同方案的轴向收缩量

将摩擦因数代入到有限元仿真中,可得到不同方案下的轴向收缩量,如图10所示。由图10可知,位移0～10 mm时不同方案存在近似结果。图10中位移10～15 mm段称为过渡段。此处主要考察过渡段及之后变化,定义收缩量占比为Ps,于是有:

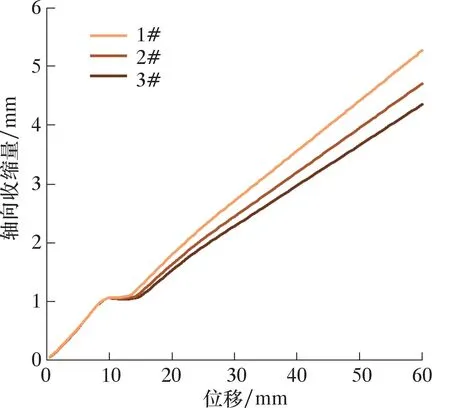
图10 不同减摩方案试验管件的轴向收缩量Fig.10 Axial contraction of test tube in different lubrication schemes

式中:L为最终位移,mm;Lo为平稳段结束位移,mm;Su为最终轴向收缩量,mm;So为平稳段轴向收缩量,mm。

结合图10与表3分析可知:①图10曲线可分为3段。第1段为锥体开始进入管内,但并未完全进入;第2段锥体逐渐进入管内;第3段锥体继续胀开试验管,此时轴向收缩量与锥体位移的关系逐渐趋于稳定。②根据图10,锥体进入试验管前,3种减摩方案试验管件轴向收缩量结果近似,此时轴向收缩量受摩擦因数影响较小;锥体完全进入管内所需位移存在差异,对不同方案下膨胀管轴向收缩量进行分析发现,摩擦因数越大,金属更易发生轴向流动,锥体更易进入试验管件内。③锥体完全进入试验管件后,轴向收缩量与锥体位移关系逐渐趋于稳定,且具有一定的线性特征,不同减摩方案具有不同的斜率。这一阶段,轴向收缩量随锥体胀入管件逐渐变大,摩擦因数越大,单位位移下的轴向收缩量越大。④以如图11所示的扇形单元,结合金属塑性成形时材料流动特性对图10所示轴向收缩量进行分析。按图11所示,管件以周向分为72份网格,径向分为8层,将每个网格作为独立的一部分。当管材以径向方向扩径时,取中间层任一小扇形部分进行受力分析,扇形受径向相邻扇形的挤压力,受轴向相邻扇形单元的压力。根据金属塑性成形原理,金属流动过程中遵循最小阻力定律,扇形单元在金属流动过程中,径向受压变薄,周向受拉变长,轴向受压变扁,宏观上的表现为壁厚减薄和轴向缩短。⑤由图11可知,随着摩擦因数增大,扇形单元所受轴向力增大,更易被压扁,单元内金属更易流向周向,表现为轴向收缩量变大。

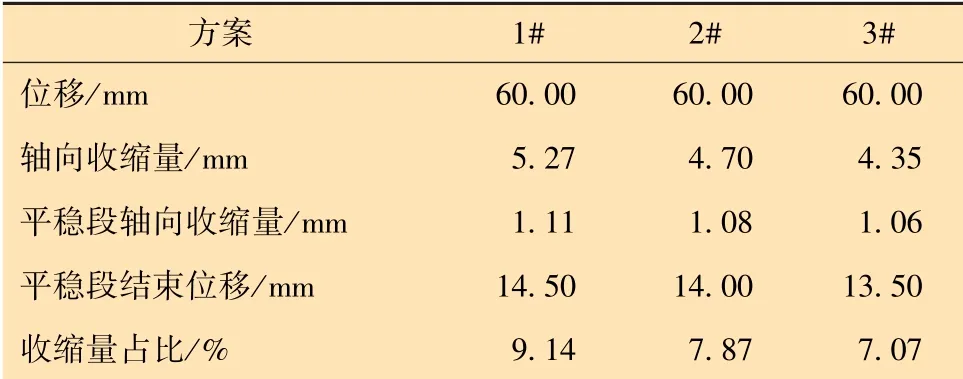
表3 不同方案下轴向收缩量占比计算Table 3 Calculation of axial contraction proportion in different schemes

图11 网格划分的扇形单元Fig.11 Sector elements of mesh division

3.4 不同方案下壁厚减薄量

将室内试验所得摩擦因数代入到有限元仿真中,可得到不同方案下的壁厚减薄量如图12所示。

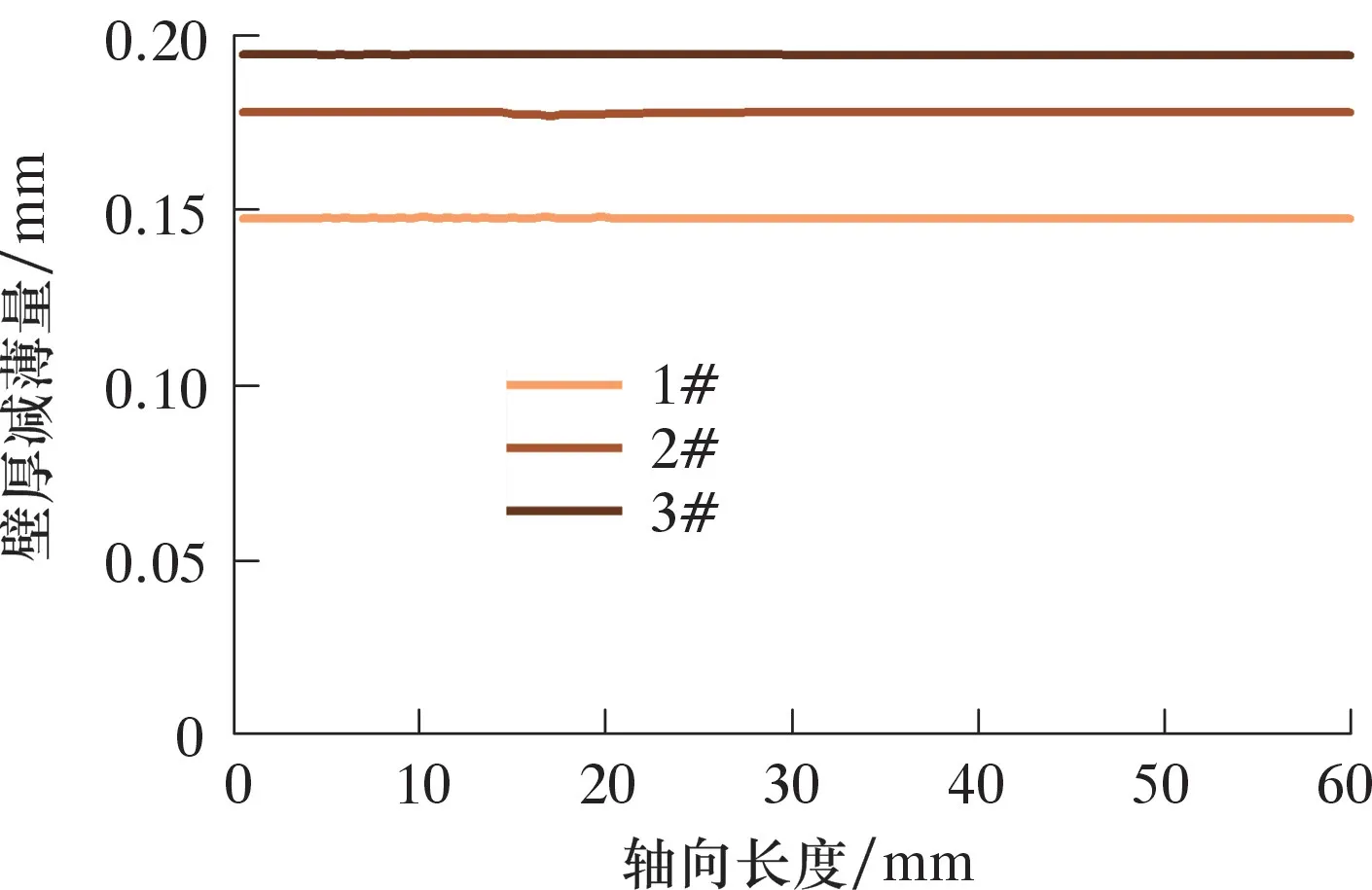
图12 不同方案下试验管件的壁厚减薄量Fig.12 Wall thickness reduction of test tube in different schemes

如定义轴向长度为L时的减薄量占比为PtL,则PtL计算如下:

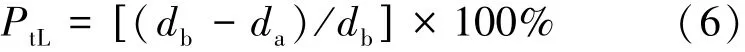
式中:da为胀后壁厚,mm;db为胀前壁厚,mm。

结合图12与表4分析可知:①在锥体完全进入试验管件后的轴向稳定段,试验管件壁厚减薄量在轴向长度上变化极小。②不同润滑方式下,壁厚减薄量不同;摩擦因数越大,壁厚减薄量越小。③根据3.3节扇形单元的受力分析,结合管件与锥体接触处的受力,接触处为斜面,摩擦力随摩擦因数上升而增大,管件接触面所受摩擦力增加,方向为沿斜面指向锥体前进方向相同一侧。将摩擦力分解为轴向和径向,可知轴向与径向力均随摩擦因数上升而增大。此时的管件内壁金属轴向更易向锥体同向流动,径向更易向圆心流动,宏观表现为壁厚减薄量减小,胀后管壁更厚。

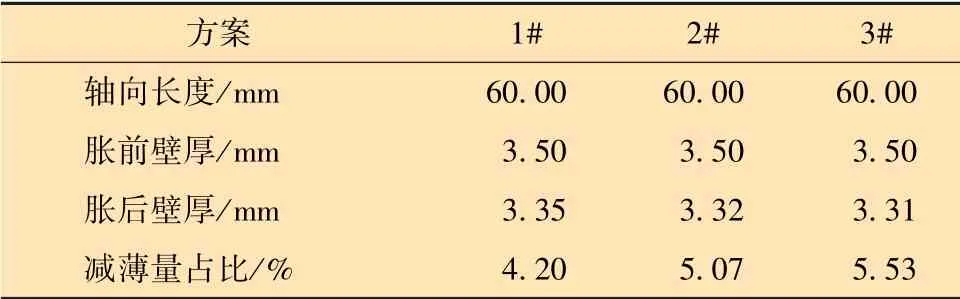
表4 壁厚减薄量数据Table 4 Wall thickness reduction data

4 结论及认识

(1)在不考虑油套管柱影响时,所需膨胀力主要取决于管材塑性变形力和膨胀过程中膨胀管和膨胀锥的摩擦力,对于指定规格、材料的膨胀管工具,降低摩擦力对膨胀管安全作业至关重要。

(2)室内冷扩管试验中,膨胀力随位移变化曲线可观察到胀入段、包覆段、待稳段、稳定段4个不同的膨胀阶段,仿真计算结果具有相同规律。

(3)3种润滑方式下,试验管件胀后的von-Mises应力分布规律相似,最大处为刚脱离锥体处管件内壁;且在壁厚方向上,内外壁应力较大,中间应力较小。

(4)本文采用的3种减摩方案,其扩管稳定阶段的膨胀力分别为62.49、51.50、和44.73 kN,证实了通过恰当的减摩降阻处理,可大幅降低膨胀力。

(5)轴向收缩量和壁厚减薄量受摩擦因数影响较大,减摩降阻对改善管件胀后力学性能有重要意义。

(6)针对冷扩管过程中接触区域摩擦因数难以实测的问题,本文通过室内管件模拟试验与仿真计算结合,获取不同润滑方式下试验管件的摩擦力及摩擦因数,提供了1种预测扩管过程中管件塑性变形减摩效果的方法。