复合月牙形磨损套管剩余强度研究*

幸雪松 武治强 张星坤 黄文君

(1.中海油研究总院有限责任公司 2.中国石油大学(北京)石油工程教育部重点实验室)

幸雪松,武治强,张星坤,等.复合月牙形磨损套管剩余强度研究.石油机械,2022,50(11):126-132.

0 引 言

钻井作业中,下入套管继续钻进时,钻柱与套管的接触在所难免。由于它们之间的接触压力,特别是钻杆旋转运动时,极易对套管内壁造成磨损[1-4]。一旦出现磨损缺陷,将破坏套管的完整性,套管的剩余强度随之下降。套管的受损将影响后续作业的进行与作业的安全性,例如地层层间作用使得套管剪切变形,使套管内径缩小导致井下工具难以下入[3-4],套管性能变化将影响井口的抬升高度等等[5]。钻井工况复杂,磨损形式也多种多样,不同的磨损形式会对套管的剩余强度造成不同的影响。

关于含缺陷套管的剩余强度研究,大体分为2种方法,即理论方法与数值模拟方法。理论方法主要针对单月牙磨损缺陷形式,提出多种剩余强度计算模型。长槽模型[6]将磨损缺陷作为矩形凹槽,通过凹槽处的环向应力与力矩来计算套管的剩余内压强度。但这样的假设只考虑了磨损深度对套管剩余强度的影响,忽略了磨损宽度对剩余强度的影响,且不适用于套管的复合磨损模式,具有一定局限性。偏心筒模型保持月牙形缺陷处最大磨损深度不变,将磨损区域扩展至整个内壁,缺陷套管近似成偏心圆筒,通过环向应力来计算剩余内压与外挤强度。王小增等[7]将套管的月牙形磨损简化为偏心圆,通过直角坐标向双极坐标的转换,得到了内壁磨损套管内、外表面应力分布的解析解。王刚庆等[8]用有限元法分析了内、外压作用下,不同磨损深度套管的偏心圆筒磨损模型和月牙形磨损模型的等效应力的差别。陈占锋等[9]采用双极坐标系和应力函数法,结合Tresca理论,导出了内壁磨损套管抗内压强度的通用解析公式。将磨损区域扩展的处理方法增加了套管的磨损宽度,使得剩余强度的计算结果与实际值会产生一定误差,且不适用于套管的复合磨损模式。等效制造缺陷模型将缺陷等效成套管制造时产生的套管不圆度与壁厚不均度,运用考虑制造缺陷的套管强度修正公式计算剩余内压与外挤强度。曾德智等[10]将月牙形磨损套管的磨损缺陷简化为套管内壁不圆度和壁厚不均度的叠加,从而来计算套管的剩余强度;廖华林等[11]将月牙形磨损缺陷套管等效成内壁不圆度和壁厚不均度的套管,将磨损缺陷扩展成椭圆来计算套管的剩余强度。这种假设方法与实际的磨损缺陷有一定差异。套管内压失效时会在磨损缺陷处产生应力集中,等效制造缺陷的方法使得应力集中效应减弱,从而产生计算误差,且模型不适用于套管复合磨损模式剩余强度的计算。

数值模拟方法一般用有限元计算软件,建立含磨损缺陷的二维或三维模型来分析磨损套管的剩余强度。郑传奎等[12]通过变分原理引入有限单元法基本方程,给出磨损边界上任意点法向量的解析解和数值解,从而求得磨损处的应力值得到套管的剩余强度。闫相祯等[13]利用有限元软件建立含磨损缺陷套管的三维有限元模型,得到不同磨损情况时套管在外挤作用时的Mises应力值。但数值模拟方法未考虑套管的复合磨损模式。判断套管失效时,基本采用套管的最大Mises应力达到材料的屈服强度来判断套管失效,但此准则较为保守,距套管失效还留有一定的空间。

现场实测数据表明,在某些井段的套管上存在多个磨损区域,磨损形状也较为复杂[14],这些因素的存在导致套管剩余强度的计算超出了常规模型的适用范围。为此,笔者开展了复合磨损套管的剩余强度试验,分析了套管失效的机理,并对不同因素对套管剩余强度的影响规律展开了分析,以期对油气井作业优化与安全控制提供参考。

1 磨损套管剩余强度试验

本文针对ø193.68 mm×12.7 mm 的TP140V套管开展磨损套管抗内压爆破强度与抗外压挤毁强度试验。

1.1 内压失效试验

1.1.1 20%磨损深度缺陷套管

为模拟井下钻柱对套管的磨损,对试验套管进行月牙形磨损,磨损最大深度d为初始壁厚的20%,磨损宽度θ为180°的20%,如图1所示。在管内注入水作为试验介质,不断加压。

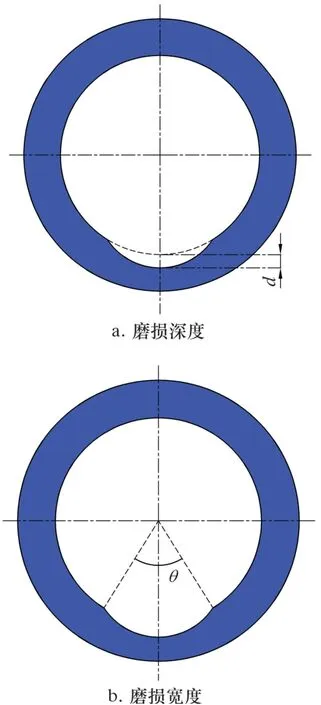
图1 磨损缺陷Fig.1 Wear defect

随着压力的不断增加,到一定程度时磨损区域处爆破,此时认定套管失效,得到套管的失效压力为147.38 MPa。

1.1.2 20%+10%磨损深度缺陷套管

对套管进行2处月牙形磨损,一处最大磨损深度为20%,另一处最大磨损深度为10%,2处磨损的磨损宽度均为20%,2处磨损最大深度之间的磨损夹角α为180°,如图2所示。

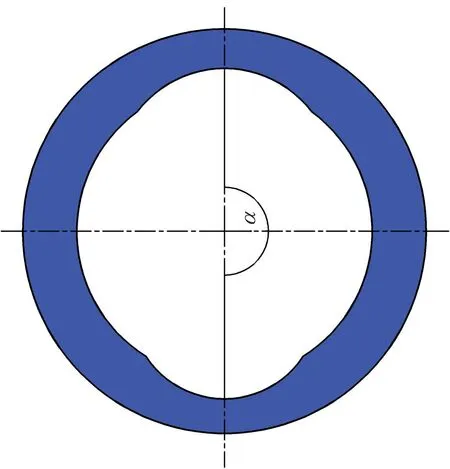
图2 磨损夹角Fig.2 Wear angle

套管失效时,20%磨损深度区域处率先出现爆破,得到套管的失效压力为146.06 MPa。

1.2 外压失效试验

1.2.1 20%磨损深度缺陷套管

对套管进行一处单月牙磨损,磨损深度与磨损宽度均为20%。将水作为试验介质,在套管外不断加压。加压到一定程度时,套管挤毁,此时认定套管失效,得到套管的失效压力为86.27 MPa。

1.2.2 20%+10%磨损深度缺陷套管

对套管进行2处月牙形磨损,一处最大磨损深度为20%,另一处最大磨损深度为10%,2处磨损的磨损宽度均为20%,2处磨损最大深度之间的磨损夹角为180°。加压到一定程度时,套管挤毁,此时,得到套管的失效压力为79.69 MPa。

2 月牙形磨损对套管剩余强度的影响

使用ABAQUS有限元软件来计算磨损套管的剩余强度,根据套管剩余强度试验,以此为基础,对计算结果进行修正。本文针对ø193.68 mm×12.7 mm TP140V套管,开展了多种磨损形式的套管剩余强度计算,来分析不同的磨损形式对套管剩余强度的影响。

模型采用二维平面模型,在套管内、外侧分别施加均布载荷,如图3所示,模型单元类型选择CPE4R。

图3 磨损套管ABAQUS模型Fig.3 ABAQUS model of worn casing

2.1 失效准则

ABAQUS有限元软件采用施加载荷的方式来分析应力、变形情况。但求套管的剩余强度相当于反向求解。已知应力变形结果求施加载荷情况,传统的失效准则为套管上最大Mises应力达到材料的屈服强度,判断套管失效,只要知道套管材料的屈服强度即已知结果条件。但此准则较为保守,距套管破裂与变形破坏强度实际值仍有一定差距。本文要建立的失效准则结果未知,这就需要和试验值对比来获取所需的结果条件。

2.1.1 内压套管失效

根据试验结果,因磨损处产生应力集中,磨损套管内压失效形式为磨损缺陷处产生爆破,故以套管缺陷处单元的Mises应力达到屈服强度的单元数量作为其失效准则。例如,缺陷处有50%的单元的Mises应力达到了材料的屈服强度,则认定套管失效,此时的内压即为磨损套管的抗内压强度。但单元数量的标准究竟为多少,需要和试验结果比较方知,如图4所示。

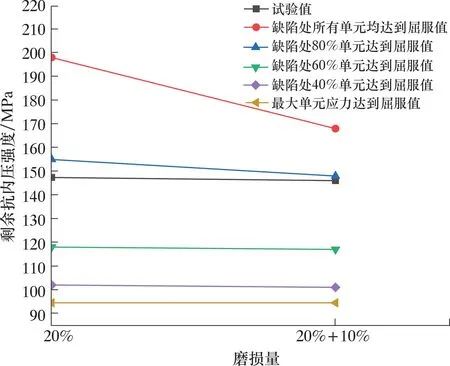
图4 不同失效准则的有限元内压强度与试验值Fig.4 Finite element internal pressure strength and test value under different failure criteria

虽然缺陷处80%单元达到屈服值时的失效载荷与试验值较为接近,但当磨损宽度较大时,由于应力集中,远离最大深度处的缺陷部分很难达到屈服强度,会使计算出的失效载荷失真。如图5所示,且20% 磨损量与20%+10% 磨损量失效载荷的下降幅度与试验值相差较大,故选用修正的(乘一个修正系数)缺陷处40%单元达到屈服应力时的内压载荷作为失效载荷最为稳妥。

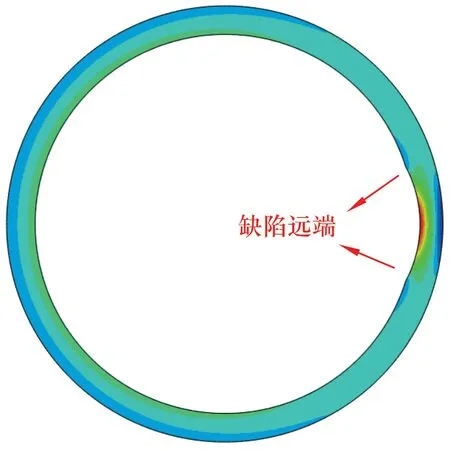
图5 抗内压失效时套管的应力云图Fig.5 Stress cloud chart of casing during failure of internal pressure resistance

2.1.2 外压套管失效

对于磨损套管外压失效,根据试验可知,失效形式为管体挤毁,为变形破坏,故以套管变形的椭圆度作为其失效准则。当套管达到5%椭圆度时,外载与试验值较为接近,如图6所示。

故将套管达到5%椭圆度作为磨损套管的失效准则,即套管达到5%椭圆度的外挤强度就是失效载荷。

2.2 套管剩余强度敏感性分析

采用控制变量法来进行套管缺陷的敏感性分析,探究不同形式的磨损缺陷对于套管剩余强度的影响。

2.2.1 单月牙磨损深度分析

为探究磨损深度对剩余强度的影响,保持磨损宽度为20%((θ/180°)×100%=20%)不变,如图7所示,改变不同的磨损深度,得出剩余强度的变化规律。

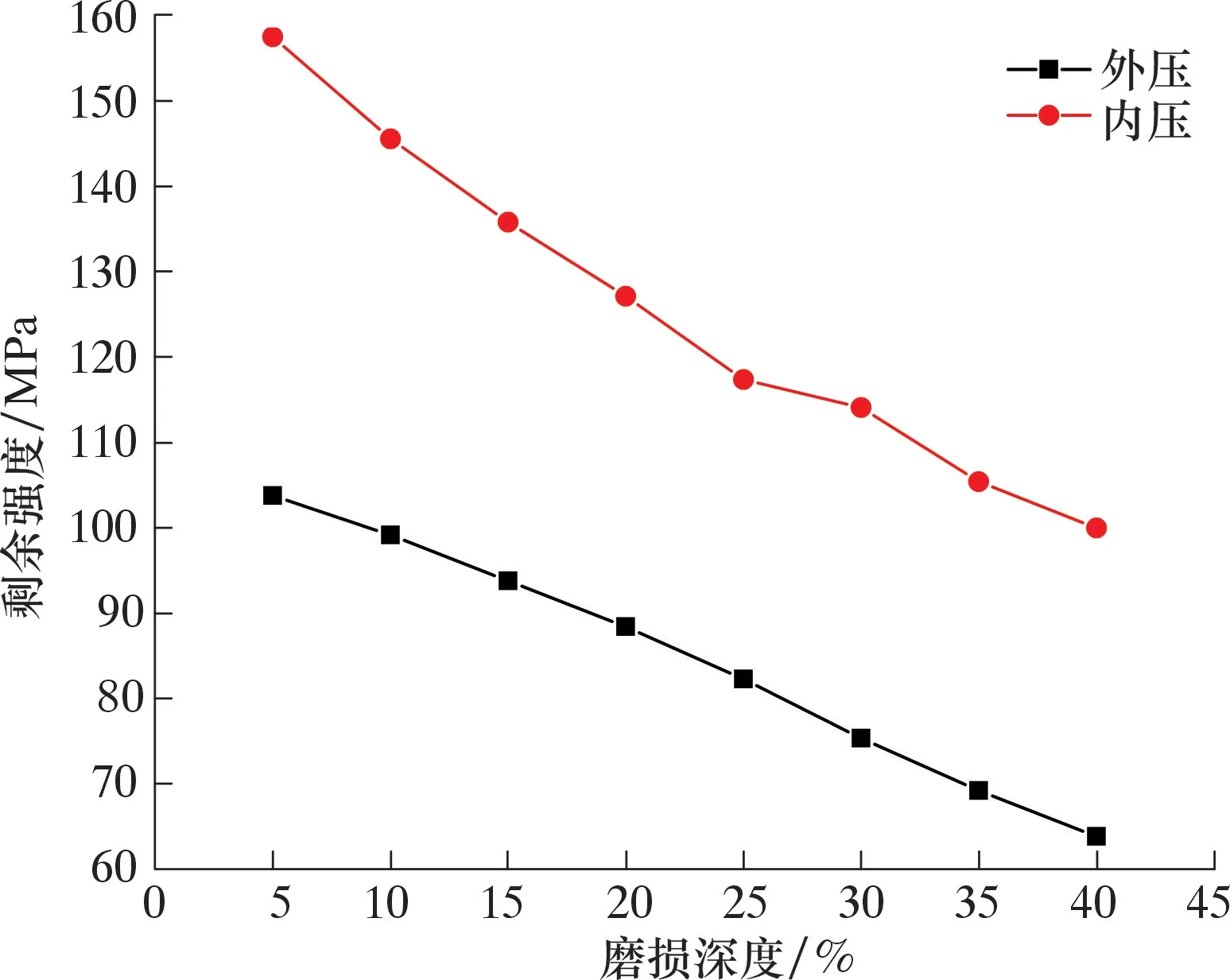
图7 不同磨损深度的剩余强度Fig.7 Residual strength with different wearing depths

由图7可知,随着磨损深度的增加,剩余抗外挤和抗内压强度都在显著下降,磨损深度从5%～40%之间,剩余抗内压强度最多下降36.56%,剩余抗外挤强度最多下降38.51%。可见磨损深度对剩余强度的影响较大。

2.2.2 单月牙磨损宽度分析

为探究磨损宽度对于剩余强度的影响,保持磨损深度为20%不变,改变不同的磨损宽度,得出剩余强度的变化规律,结果如图8所示。

图8 不同磨损宽度的剩余强度Fig.8 Residual strength with different wearing widths

由图8可知,随着磨损宽度的增加,剩余抗外挤强度逐渐降低,剩余抗内压强度逐渐增高。磨损宽度从10%增大到50%,抗内压强最多升高8.59%,抗外挤强度最多下降17.6%。因为外挤失效是由于套管变形过大,缺陷截面挤毁。内压失效是由于缺陷处破裂,磨损宽度减小会使缺陷处应力集中。

2.2.3 磨损深宽比分析

图9所示为抗内压强度与深宽比(缺陷的磨损深度/磨损宽度)的关系。由图9可知,抗内压强度随着深宽比的增大而减小。故抗内压破坏时,深宽比与剩余强度具有相关性,可将深宽比作为判断内压失效的依据。如此,便可将影响剩余强度的2个因素简化成一个因素,可以减少试验次数。例如,要分别分析磨损深度与磨损宽度对抗内压强度的影响,有了此结论,便可只分析深宽比对剩余强度的影响。

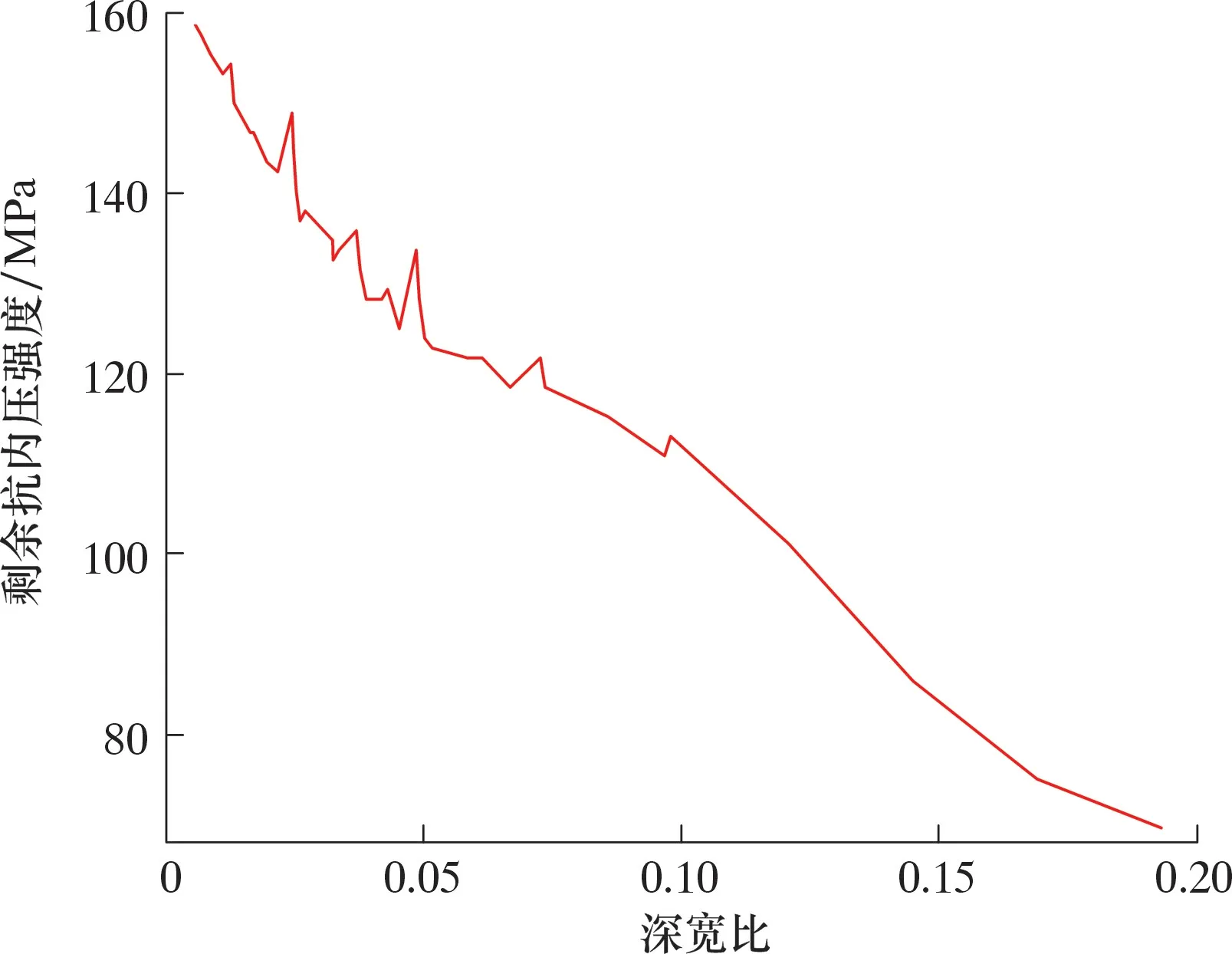
图9 不同深宽比的抗内压强度Fig.9 Internal pressure strength of different depth-to-width ratio

2.2.4 双月牙内压强度分析

保持第1处磨损深度为20%、宽度为10%,第2处磨损宽度为10%不变;改变第2处的磨损深度,即改变第2处的深宽比。

套管2处磨损内压破坏时,以深宽比较大的磨损为主磨损,深宽比较小的磨损为次磨损,如图10所示。

2处磨损时,次磨损深宽比的增加,对抗内压强度影响很小,次磨损深度增加5%,对强度的影响平均为0.17%,这是因为内压破坏发生在主磨损上。主磨损的增加会使抗内压强度明显减小,主磨损深度增加5%,抗外挤强度平均减小9.81%。

抗内压强度整体会随着磨损夹角的增大而减小。当磨损夹角增大30°时,抗内压强度平均减小1.03%。

2.2.5 双月牙外挤强度分析

(1)改变一处磨损深度。保持第1处磨损深度为20%、宽度为10%,第2处磨损宽度为10%不变,改变第2处的磨损深度。

套管2处磨损外挤破坏时,2处磨损宽度相同,以磨损深度较大处的缺陷为主磨损,另一处即为次磨损,如图11所示。

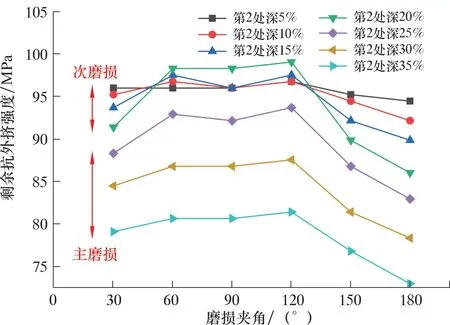
图11 改变一处磨损深度的抗外挤强度Fig.11 Internal pressure strength when changing wearing depth at one place

由图11可知,抗外挤强度会随着一处磨损深度的增加而减小。次磨损深度增加5%,抗外挤强度平均减小0.67%;主磨损深度增加5%,抗外挤强度平均减小5.97%。

抗外挤强度在60°～120°之间较大,趋于平缓,在两边减小。当高于120°时,夹角增大30°,抗外挤强度平均减小4.57%;当低于60°时,夹角减小30°,抗外挤强度平均减小3.38%。

(2)改变一处的磨损宽度。保持第1处磨损深度为20%、宽度为20%,第2处磨损深度为20%不变,改变第2处的磨损宽度。当磨损宽度较大,2处磨损缺陷夹角较小时,会使2处缺陷融合成一处缺陷。故磨损夹角不可太小,分析的夹角范围为120°～180°。

套管2处磨损遭外挤破坏时,2处磨损深度相同,以磨损宽度较大处的缺陷为主磨损,另一处即为次磨损。抗外挤强度会随着一处磨损宽度的增加而减小。次磨损宽度增加5%,抗外挤强度平均减小1.75%;主磨损深度增加5%,抗外挤强度平均减小2.38%,如图12所示。

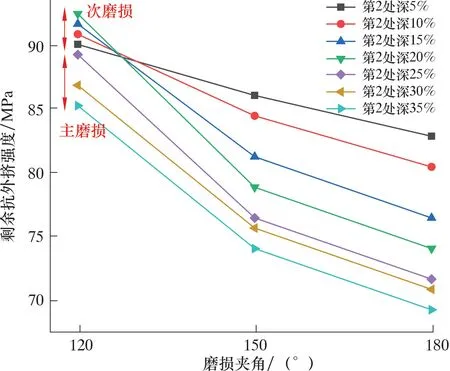
图12 改变一处磨损宽度的抗外挤强度Fig.12 Internal pressure strength when changing wearing width at one place

3 结 论

(1)开展了套管剩余强度试验,得到了不同缺陷形式下套管的抗外挤与抗内压强度试验值,为后续剩余强度的计算提供了保障。

(2)依据剩余强度试验值,形成一套有限元计算判断套管破坏的失效准则,与传统的准则相比更接近套管的破坏强度,即剩余强度的极限值。

(3)磨损深度对于套管剩余强度的影响最为敏感,磨损深度的增加使套管抗外挤、内压的强度均减小,应规避在同一位置持续磨损。

(4)次磨损槽对抗内压强度影响较小,这是因为内压失效是一种强度失效,主要从最薄弱点(即主磨损位置)开始失效;次磨损槽对抗外挤强度影响明显,这是因为外挤失效是不稳定性问题,次磨损槽会影响套管稳定性。