脉冲对空化射流影响机理研究*

周传喜 陈伟华 潘忠义 管 锋 刘先明 万 锋

(1.长江大学机械工程学院2.胜利油田德利实业有限责任公司)

周传喜,陈伟华,潘忠义,等.脉冲对空化射流影响机理研究.石油机械,2022,50(11):30-36,42.

0 引言

水射流技术自19世纪发展至今,由于其独特的能量转换途径和环保特色,受到世界石油领域的青睐。近些年,脉冲射流和空化射流逐渐兴起,为了提高流体的空化效果,专家学者根据空化原理设计了一系列的流体空化装置[1-4]。风琴管自振空化射流喷嘴、Helmholtz型自振空化喷嘴等典型喷嘴以及井下解堵工具逐渐面世,被应用于油罐清洗、井下解堵、钻头钻井等诸多作业中。

李根生等[5-8]分析了风琴管自振空化射流喷嘴的空化发生原理,对风琴管谐振腔的固有频率计算公式进行推导,给出了谐振腔基本结构的设计模式;在此基础上,进一步得到了满足不同钻井工况的自振空化喷嘴设计方法。朱成龙[9]对空化现象和空化泡演变过程进行研究,依据流体动力学对3种空化喷嘴进行模拟试验,为流体空化应用于油气井增产提供了依据。易灿等[10]依据瞬态流和水声学研制了自振空化喷嘴,通过试验证实了自振空化喷嘴比普通锥形喷嘴具有更大的起始空化数和更强的空化起始能力。韦志超[11]通过数值模拟探究了基于附壁效应的自激脉冲喷嘴相关机理和性能,验证了附壁式自激脉冲喷嘴的可行性,得出了附壁式自激脉冲喷嘴参数对性能的影响规律。曲洪娜等[12]对水平井旋转射流冲砂洗井机理进行研究,形成了一套水平井旋转射流冲砂洗井水力参数设计方法。王循明[13]首次将脉冲喷射清洗方式引入大型油罐底泥清洗,并建立了自激脉冲喷嘴数值优化理论,得到了自激喷嘴结构运行参数的优化配比范围。

综上,空化射流和脉冲射流已经普遍应用于石油领域内,而风琴管自振空化射流喷嘴、自激脉冲喷嘴以及井下解堵工具等常常是空化和脉冲射流同时使用。目前脉冲和空化射流理论各自研究较多,但二者结合研究鲜有涉及,脉冲对空化效果的作用机理尚不明确。为此,笔者建立了空化喷嘴模型,开展了脉冲参数对空化特性的影响研究,为指导空化射流类工具的设计以及工程应用中流体参数控制提供理论依据。

1 空化模型的建立

开展脉冲参数对空化特性的影响研究,首先需要分析脉冲空化射流理论,在此基础上建立空化喷嘴模型。同时对建立的有限元模型进行网格无关性验证,在确保计算结果精度的前提下,尽可能提高计算效率。

1.1 脉冲空化射流理论

空化是指流体在流动过程中,由于管道结构或者外在条件发生变化,导致流体局部压力低于当前流体饱和蒸汽压,流体内部的微小气泡(气核)在短时间内迅速膨胀并溃灭,释放大量能量的现象[14-16]。空化射流工具设计的基本原理就是人为创造空化条件或者改变管道结构使流体压力降低,诱使射流工具中空化的产生。在研究空化射流时,将单个空泡的孤立状态作为研究对象,分析空泡周围压力变化。忽略水中气体扩散,空泡静止状态下的平衡方程为:

式中:p为空泡周围壁面上的水体压力,Pa;pv为泡内的饱和蒸汽压力,Pa;R为空泡半径,m;σ为水的表面张力系数,N/m。

根据式(1)推导可知,空化膨胀条件为:

脉冲射流相比于连续射流,在一段时间内,相同入口流量下,流体速度具有更高峰值,即更低的射流压力,有利于空化气泡的初生和发展。同时脉冲射流在出口淹没区域中会产生剪切现象,形成不稳定漩涡。淹没射流中不稳定漩涡的产生会提供低压区域,进一步增强空化效果。根据经典的兰金涡模型,流场在涡环中心形成压力降,其大小可用下式表示[17]:

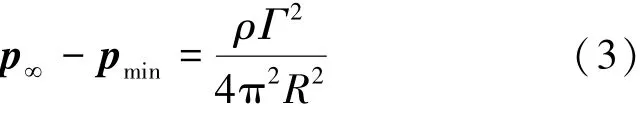
式中:ρ为流体密度,kg/m3;Γ为涡的环量,m2/s;p∞为无穷远处压力,Pa;pmin为漩涡中心压力,Pa。

根据式(3)可得,Γ越大,涡环中心的压力降将会越大,从而促使淹没条件下空化的形成。

1.2 空化模型的建立

空泡的初生、发育、溃灭都在极短的时间内完成,因此空化射流的主要元件为工具最末端的空化喷嘴。根据不同空化类型的原理,常见空化喷嘴有角形空化喷嘴、亥姆霍兹空化喷嘴和风琴管空化喷嘴。但亥姆霍兹空化喷嘴和风琴管空化喷嘴自身存在振荡结构,会对入射脉冲产生影响,因此本文采用角形空化喷嘴。角形喷嘴模型主要结构尺寸如图1所示,其入口直径D=8 mm,缩颈段长度L=25.35 mm,圆柱段长度L1=5 mm,喷嘴圆柱段直径d=2 mm,扩散段长度L2=8 mm,扩散角θ=60°[7]。

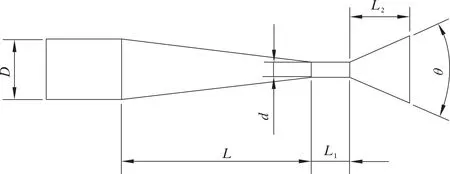
图1 角形喷嘴模型Fig.1 Angular nozzle model

为减少运算量,采用二维计算模型,利用Workbench软件中的DesignModeler模块完成角形喷嘴的几何建模,外部流场域为长100 mm、宽为700 mm的长方形。对模型进行网格划分,如图2所示。

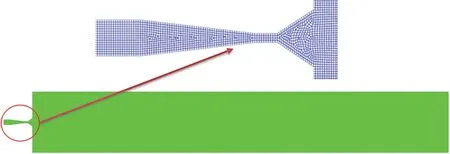
图2 有限元计算模型Fig.2 Finite element model

采用Mixture模型和k-εStandard模型[18]。设置第1相为水,密度为998.2 kg/m3,黏度为0.001 003 Pa·s;第2相 为 水 蒸 气,密 度 为0.554 2 kg/m3,黏度为0.000 013 4 Pa·s。水与水蒸气转化模式为cavitation,转化压力为2 338.8 Pa[9]。设置进口第1相速度为35 m/s,出口采用混合压力出口,为一个大气压(即0.1 MPa),利用SIMPLE算法进行瞬态计算。

1.3 网格无关性验证

为了保证计算的精度以及运行速度,对建立的空化模型进行网格无关性验证,如图3所示。由图3可知,当网格单元数量大于20万后,网格数量对计算结果的影响不大,因此网格数和节点数分别选择为286 751和288 447,以保证计算结果的准确性和可靠性。

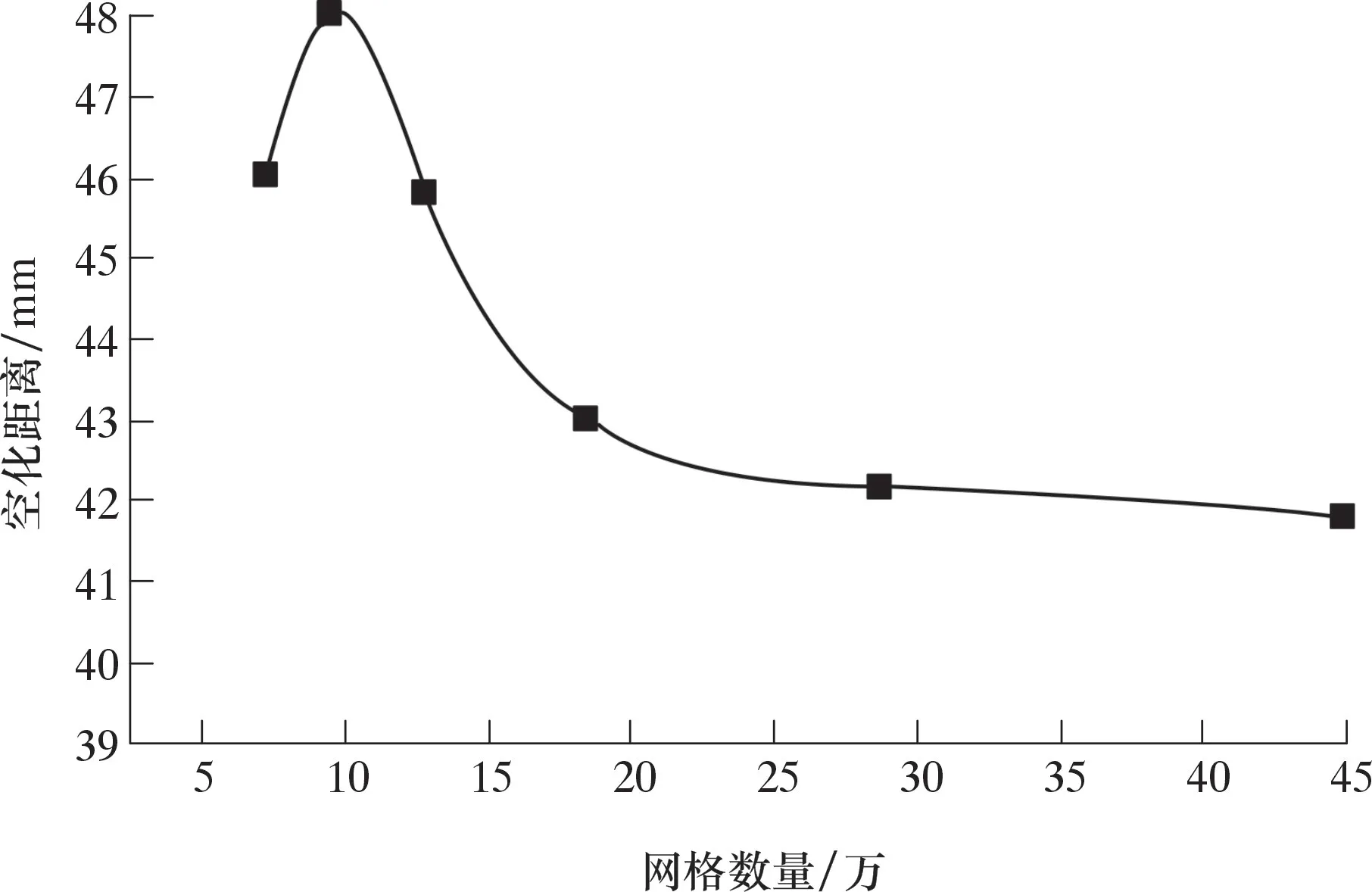
图3 网格验证Fig.3 Grid validation

1.4 有限元分析结果

喷嘴以及外流场区域的连续射流速度云图和第2相体积分数分布云图如图4所示。由图4可知,射流速度在缩颈段逐渐提升,且由于与外流场区域的流体发生了剪切作用,在扩散段以及外围流场中速度逐渐减小。体积分数越高,空化效果越好。水蒸气在圆柱段开始出现,在扩散段体积分数急剧增加,最高可达95.4%,又在尾端迅速下降直至降为0。此过程表明空化泡在圆柱段初生,在外流场区域迅速发展、溃灭。

图4 连续射流结果云图Fig.4 Cloud chart of continuous jet results

空化作用的强弱可以通过对气相分布区域面积大小、气相体积分数以及空化距离进行评价,而空化工具往往需要进行喷射作业,因此笔者以空化距离作为主要评价指标[9]。空化作用发挥的主要区域在喷嘴出口处,连续射流空化距离最远为42.17 mm。

2 脉冲对空化射流参数影响分析

脉冲类型、幅值和周期是衡量脉冲射流的主要参数[19-21]。为了研究脉冲射流对空化作用的影响,以建立的有限元模型为基础,以类型、幅值和周期为变量,利用Visual Studio软件编写编译型udf文件,在User Defined自定义功能中,动态链接入Fluent中,在边界条件inlet中将自定义函数文件导入速度入口中,设定脉冲入射自定义函数。

2.1 不同脉冲类型对空化的影响

脉冲主要指一个物理量在短持续时间内突变后迅速回到其初始状态的过程。常见脉冲类型有正弦形脉冲函数、梯形(矩形)脉冲函数、锯齿形(三角)脉冲函数。根据脉冲函数的类型和参数,设定脉冲入射流速。在喷嘴入口处设置监测点,监测入口速度,实时监测速度变化,其入口速度随时间变化如图5所示,其值变化与设定脉冲入射自定义函数一致。

图5 入口脉冲监测图Fig.5 Inlet pulse monitoring diagram

图6为正弦脉冲入射流在出口处第2相体积分数云图随时间变化过程。由图6可见,空化距离随时间周期性变化,随着脉冲信号而波动,其距离最小值为31.5 mm,距离最大值为50.8 mm。由于脉冲射流具有间断性的特点,增强了淹没流体区域的剪切流,产生了漩涡,因而在淹没流体区域出现了第2次空化现象,下文简述为二次空化。相比于喷嘴的稳定空化区域,二次空化的稳定性较低,但喷射距离更远。

图6 正弦脉冲结果云图(第2相体积分数)Fig.6 Cloud chart of sinusoidal pulse results

3种脉冲射流中,矩形脉冲射流二次空化效果 最为明显,其过程如图7所示。分别对矩形脉冲和三角脉冲入射流进行仿真分析,在一段时间内,相同入射流量下,连续射流最大空化距离为42.2 mm;而脉冲入射流对于第1次空化作用距离有显著的增强作用,其中矩形脉冲射流空化喷射距离最远为72.7 mm,空化效果提升可达72.27%,但存在周期内空化效果消失的现象。三角脉冲射流空化最长距离为51.6 mm,效果提升为22.27%,最短距离为35.6 mm。而正弦脉冲射流最长距离为51.8 mm,效果提升22.74%,最短距离空化作用为31.5 mm。

图7 矩形脉冲空化云图(第2相体积分数)Fig.7 Cloud chart of rectangular pulse cavitation

以空化距离为主要评价指标,矩形脉冲二次空化效果较强,正弦和三角脉冲二次空化效果一般,连续射流无二次空化现象。表1为不同脉冲类型有限元仿真结果。

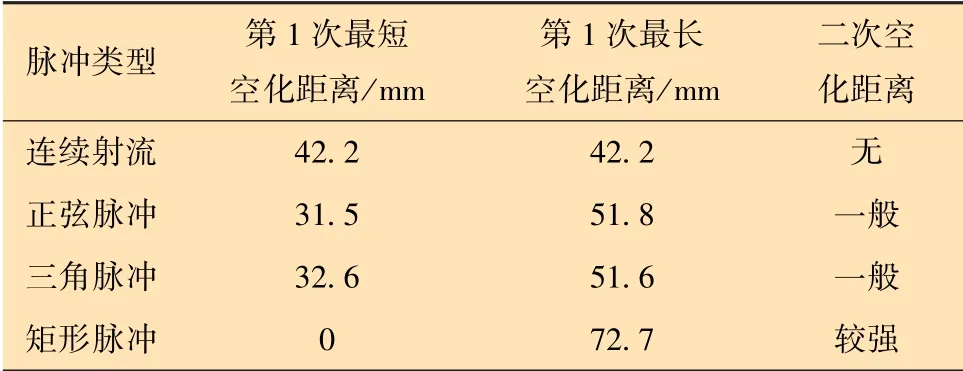
表1 不同脉冲类型有限元结果Table 1 Finite element results of different pulse types

综上,脉冲入射流对空化射流的形成具有促进作用。在实际应用中,空化作业应优先考虑脉冲入射流;空化工具的设计和改造应该充分考虑振荡结构对空化效果的促进作用。其中矩形脉冲第1次空化作用距离最远且第2次空化较强,适用于大井眼除砂解堵以及油罐清洗等较远距离作业;正弦脉冲和三角脉冲空化的第1、2次空化距离相较矩形脉冲较短,但空化作用持续时间长,适用于小井眼除砂解堵等近距离作业。

2.2 脉冲幅值对空化的影响

考虑脉冲的稳定性,本节将以正弦脉冲为研究对象,开展脉冲幅值对空化作用的影响研究。设定入射脉冲速度幅值分别为1、2、3、4、5、6、7、8和9 m/s,开展有限元仿真,结果如图8、图9所示。

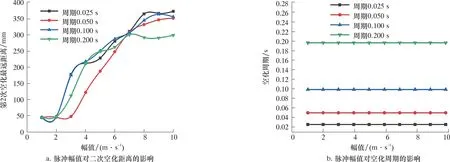
图9 脉冲幅值对二次空化的影响Fig.9 Influence of pulse amplitude on the second cavitation

由图8可知:随着脉冲幅值的增加,第1次空 化作用最远距离整体呈现上升趋势,上升速度逐渐趋于平稳,幅值为10 m/s时,脉冲周期为0.025 s的入射流空化距离最远,为76.92 mm;第1次空化作用最近距离整体呈现下降趋势,下降速度逐渐趋于平稳,幅值为10 m/s时,脉冲周期为0.2 s的入射流最短空化距离值最小,为29 mm。

由图9可知:随着脉冲幅值的增加,第2次空化最远距离逐渐增加并趋于平稳,周期为0.025 s,幅值为10 m/s时,第2次空化最远距离值最大,为372.34 mm;脉冲幅值的改变对空化周期并无影响。

2.3 脉冲周期对空化的影响

本节将以幅值为5、6、7和8 m/s的正弦脉冲为研究对象,开展脉冲周期对空化作用的影响研究。设定入射脉冲周期分别为0.1、0.2、0.3、0.4、0.5、0.6和0.7 s,开展有限元仿真,结果如图10所示。根据图10可以看出,脉冲周期的变化对第1次空化距离的影响较小,整体变化趋于平稳;相比于低幅值脉冲射流,脉冲周期对高幅值脉冲射流的二次空化影响较大,即脉冲周期的增大会减弱第2次空化;幅值为8 m/s的脉冲入射流在周期为0.1 s时,第2次空化最远距离可达到344.26 mm,但周期在0.7 s时第2次空化最远距离仅有286.89 mm。脉冲周期直接影响空化周期,两者呈线性关系。

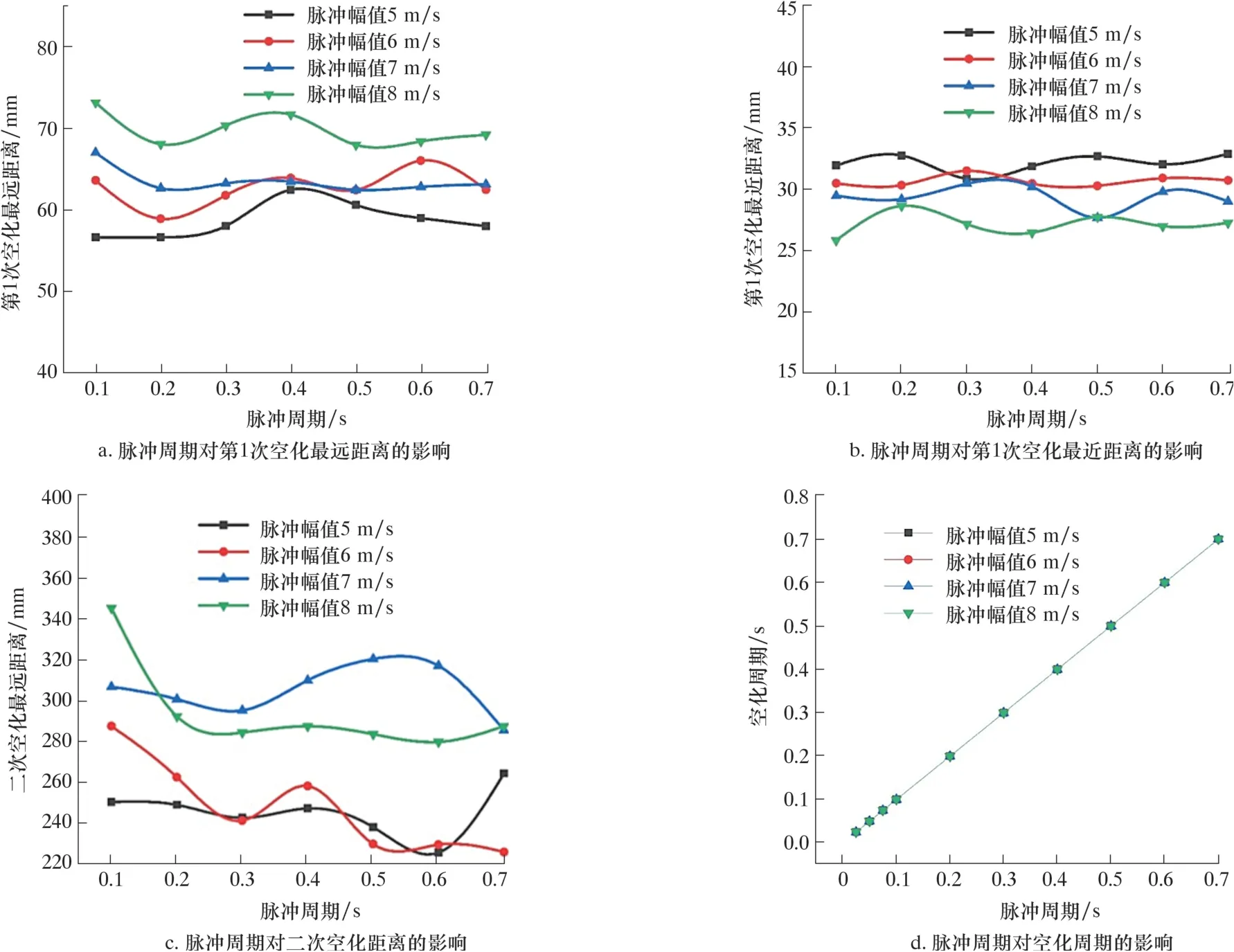
图10 脉冲周期对空化的影响Fig.10 Influence of pulse period on the cavitation

基于脉冲幅值和周期对空化作用的影响规律,在工程作业中,流体参数控制首先考虑加大脉冲幅值促进空化产生;在高幅值脉冲空化作业下,再考虑缩短脉冲周期,进一步提升空化效果。

3 结论

(1)笔者利用Workbench Fluent和Visual Studio软件建立了空化喷嘴有限元计算模型,开展了不同脉冲射流类型、幅值和周期下的空化特性研究,揭示了脉冲对空化射流的影响规律。

(2)脉冲射流对空化的形成具有较大的促进作用。矩形脉冲射流空化效果提升72.27%;三角脉冲射流空化效果提升22.27%;正弦脉冲射流空化效果提升22.74%。且在喷嘴出口淹没区域出现了二次空化现象,进一步加大了空化作用距离,增强了空化作用效果。

(3)不同脉冲类型、幅值和周期对空化作用都有显著的影响。其中矩形脉冲适用较远距离作业;正弦脉冲和三角脉冲适用于近距离持续空化作业。在工程作业中,流体参数控制首先考虑加大脉冲幅值促进空化产生,再考虑缩短脉冲周期,进一步提升空化效果。