基于特征曲线法的围岩-支护系统安全性分析
赵昌杰,饶军应,熊 鹏,王亚奇,陈 忆
(1.贵州大学土木工程学院,贵州 贵阳 550025;2.贵州大学空间结构研究中心,贵州 贵阳 550025)
1 概述
近年来高速公路、高速铁路等系统交通工程的建设日新月异,隧道工程亦随之迅速发展。尤其在西南山区,高速公路及高铁的隧道占比高,埋深大,所处地质较复杂,支护结构设计困难。以往的隧道稳定性分析及支护结构设计方法包括数值法[1- 2]、经验法[3- 4]和解析法[5- 9]等,但通常依靠经验类比,不能充分反映围岩及支护结构的平衡关系。而特征曲线法[10- 14]视围岩为主要的承载单元,充分考虑了围岩-支护系统的相互作用,支护的本质作用是“调动围岩承载”和“协助围岩承载”[15]。特征曲线法是国际隧道协会(ITA)归纳的4种隧道结构设计模型之一[16],广泛应用于新奥法,其核心思想是将围岩视作隧道的主要承载单元,隧道开挖时允许围岩有一定的变形量,使之在隧道周围形成承载环,但又采取薄层支护手段对变形严格控制,避免隧道变形过大而失稳。该方法是通过围岩特征曲线和支护特征曲线的交汇确定隧道支护体系的平衡点,围岩和支护结构是其中2个关键的因素,它们的相互作用机理对围岩稳定性的分析有重要的作用。
唐雄俊[17]最早提出了特征曲线法思想,Fairhurst[18]亦应用弹塑性原理,指出了围岩特征曲线是一条随着初始地应力逐渐释放,围岩变形逐渐增大的曲线。之后,Bernaud[19]验证了特征曲线法在深埋隧道中的适用性。在理论方面,张常光等[20]基于统一强度理论和非关联流动法则,推导了深埋圆形岩石隧道围岩特征曲线解析新解;苏永华等[21]基于并联体系原理,导出了组合支护结构特征函数,并结合收敛-约束原理构建了支护结构稳定性系数计算方法;晏勤[22]考虑锚杆对围岩的加固效应,通过均匀化方法,推导了锚杆加固作用下的圆形隧道复合岩体围岩特征曲线解析解。在围岩特征曲线影响因素方面,金丰年[23]考虑了时间效应对围岩特征曲线的影响;张素敏等[16]选择弹塑性有限元方法,作出了各种围岩级别和不同埋深下的单、双线毛洞的围岩特征曲线。在支护时机和支护刚度选择方面,陈峰宾[24]给出了考虑喷射混凝土硬化的软岩隧道支护时机的确定方法和初期支护安全性能评价方法;张子龙等[25]提出了基于收敛约束原理和围岩局部安全评价方法单元状态指标的初期支护时机确定方法。
本文基于弹塑性原理,推导了深埋隧道围岩位移计算理论,阐述了围岩特征曲线(Ground Response Curve,GRC)与支护特征曲线(Support Characteristic Curve,SCC)及纵向变形曲线(Longitudinal Deformation Profile,LDP)的对应关系,并引入围岩稳定安全系数、支护结构安全系数和围岩变形控制率对支护起点和支护刚度的选择进行综合评价,进而定性分析了围岩级别、隧道埋深和隧道洞径对围岩特征曲线的影响,最后利用该理论对实际工程案例进行应用、指导。
2 围岩力学特性
2.1 围岩应力状态与破坏
当硐室开挖后,岩体出现临空面,随着应力局部释放,围岩向洞内发生挤入变形。由于变形,初始应力场状态发生应力的重分布,即二次应力场。对于弹塑性岩体,其应力-应变关系呈非线性,当洞周切应力满足岩体屈服条件时,围岩即进入塑性状态,塑性区使应力向围岩深部不断延伸。隧道硐室不加以支护,随着围岩应力和强度的降低,即出现松动区,此时围岩裂隙不断发展,松动区不断增大,围岩出现塑性滑移,硐室即将发生失稳破坏。弹塑性岩体中的应力图形如图1所示:
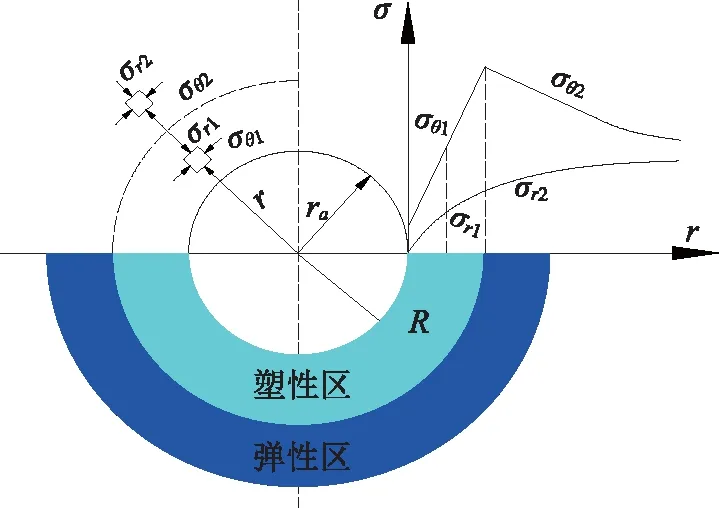
图1 围岩应力状态分布图
2.2 围岩塑性判据
圆形隧道开挖问题计算模型如图2所示,围岩初始应力场为:
σz=γh,σx=λγh
(1)
式中,σz—自重应力场下的竖直应力,MPa;σx—自重应力场下的水平应力,MPa;λ—侧压力系数;γ—围岩容重,kN/m3;h—隧道埋深,m。
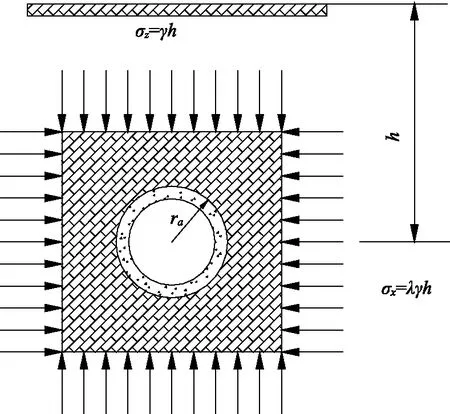
图2 圆形隧道开挖问题计算模型
在弹塑性分析中,常选用Mohr-Column条件作为塑性判据,亦称屈服准则[26]。式(2)便是现在常采用的硐室围岩塑性区的塑性判据。
σθ1-ξσr1-Sc=0
(2)

本文研究的是侧压力系数λ=1的轴对称隧道问题。此时,硐室周边的σθ=2σz,σr=0。将此式带入式(2)得:
2σz-Sc=0
(3)
使σz=γh,即得轴对称隧道壁围岩进入塑性状态的判别式:
2γh≥Sc
(4)
2.3 围岩弹塑性分析
2.3.1塑性区的应力场
取塑性区内的任意一点进行分析,其需满足平衡方程,在λ=1的条件下,其极坐标平衡方程为:
(5)
另还需满足屈服条件,由(2)式得:
将σθ1代入(5)式计算得:
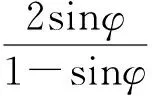
(6)
此时考虑支护阻力Pa的作用,即在r=ra时,σr1=Pa,得积分常数:
代入(5)、(6)式得:
将Sc、ξ代入得:
(7)
2.3.2弹性区的应力场位移场
当塑性区过渡到弹性区,其应力状态仅受原岩应力状态和塑性区边界应力的影响。弹性的应力解答仍属于无限弹性平面内的孔口问题,只需注意边界条件有所差别:
在无限远处(r=∞)有:σr2=γh。
在r=R处有:
σr2=σr1=σR,σθ2=σθ1
(8)
对于轴对称问题(λ=1),围岩应力在弹性力学里有现成的G.Lame公式解答[22]:
(9)
(10)
式中,G—围岩的剪切模量,GPa;v—围岩切向位移,m。
在r>R处,考虑为作用有支护阻力Pa=σR,可得弹性区应力、位移解答:
(11)
(12)
当r=ra时,即得隧道洞周弹性围岩解答:
(13)
2.3.3塑性区半径
弹塑性边界面上的应力既应满足塑性条件,又应满足弹性条件,将(11)式中的2式相加,消去σR,即得弹塑性边界上应力弹性条件为:
σr2+σθ2=2σz
(14)
结合(8)式,即得弹塑性边界上应力塑性条件:
σr1+σθ1=2σz
(15)
将式(2)、(14)和(15)联立求解,即可解出在r=R处的应力:
(16)
将r=R代入式(7),并联立式(16),即可求出塑性区半径显示表达式:
(17)
当R=ra时,即表示围岩出现塑性区的临界点,将R=ra代入(17)式得不形成塑性区时所需的支护阻力:
Pa0=σz(1-sinφ)-c·cosφ
(18)
始终,Pa0为不形成塑性区所需的支护阻力。
2.3.4塑性区的位移场
假定围岩塑性区内的岩体在小变形的情况下体积不变,得:
εr1+εθ1+εz1=0
(19)
结合平面应变状态下的几何方程得:
代入式(19)得:
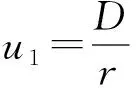
式中,D—待定系数,可由弹塑性边界上的位移协调条件ur1=ur2,并联立ur1、ur2解得塑性区位移表达式为:
(20)
将R代入ur1,并令r=ra即可解出隧道壁径向位移ura与支护阻力Pa的关系式,即围岩特征曲线函数(GRC):
(21)
因式(21)的适用对象为圆形断面隧道,对于非圆形隧道断面,本文选用“当量半径法”[27]进行转化。即假想存在一个虚拟圆,其面积等于实际非圆形隧道断面面积,其当量半径为:
(22)
式中,RD—当量半径,m;S—非圆形隧道断面面积,m2;f—断面形状修正系数,取值见表1:

表1 地下洞室断面形状修正系数[27]
3 支护特征曲线
3.1 喷射混凝土
采用下式[24]计算喷射混凝土支护刚度Kc(N/m):
(23)

式中,Ec—喷射混凝土弹性模量;μc—喷射混凝土泊松比;dc—喷射混凝土厚度。
喷射混凝土的最大支护阻力为:
(24)
式中,Jc—喷射混凝土抗压强度。
喷射混凝土允许的极限变形量为:
ulim,c=Pmax,c/Kc
(25)
3.2 锚杆
锚杆的受力条件比较复杂,常采用以下近似公式[28]确定其受拉刚度Kb:
(26)
式中,db—锚杆的直径;l—锚杆长度;fx—锚杆的横向间距;fy—锚杆的纵向间距;η—锚固端和锚固头的荷载变形常数。锚杆最大承载力(Pmax,b)采用下式:
(27)
式中,Qbf—锚杆抗拔试验破坏荷载。
锚杆允许的极限变形量为:
ulim,b=Pmax,b/Kb
(28)
3.3 钢拱架
钢拱架刚度Ks采用Oreste[29]提出的理论公式:
(29)
式中,Es—钢拱架弹性模量;Ws—各钢拱架横截面面积;fs—钢拱架纵向间距;hs—钢拱架横截面高度。
钢拱架最大承载力Pmax,s采用下式:
(30)
式中,σs—钢拱架的屈服强度。
锚杆允许的极限变形量为:
ulim,s=Pmax,s/Ks
(31)
3.4 组合支护结构
Carranza-Torresa[30]认为组合支护结构的组合刚度K等于各支护单元刚度Ki之和:
(32)
假定围岩和支护结构紧密接触,围岩对支护结构的反力也是径向分布的,组合支护结构与其径向支护阻力可采用以下表达式:
Pmax=Kumin
(33)
式中,Pmax—组合支护结构最大支护力;umin—组合支护结构允许径向位移,取各支护单元中最小极限位移,即umin=min{ulim,c,ulim,b,ulim,s}。
由上述成果可得SCC的函数表达式:
Pz=K(u-u0)
(34)
式中,Pz—组合支护结构支护力;u—隧道径向位移;u0—支护起点处隧道径向位移。
3.5 合理支护起点和支护刚度评价方法
GRC和SCC的关系如图3所示。初期支护施作起点(u0)和刚度(K)影响着围岩和支护结构的平衡效果(E点),本文引入围岩位移安全系数(Q1)、支护结构安全系数(Q2)和围岩变形控制率(Ψ)对合理支护起点和支护刚度进行综合评价。

图3 围岩与支护结构的相互作用关系
3.5.1围岩稳定安全系数
隧道围岩支护系统是一个复杂的综合体,有众多因素对隧道支护安全性产生影响,其中围岩力学状态尤为重要。而实际施工中,围岩的性质和状态均不易监测,但围岩及支护系统的位移量可反映出围岩位移状态,位移量监测简单易行。故选用基于围岩位移量的安全性评价方法[24]。
(35)
式中,Q1—围岩稳定安全系数;ulim—隧道周边围岩允许最大位移量(D点位移值);ueq—初期支护与围岩变形平衡时围岩位移值;u0—初期支护开始支护时围岩位移。
3.5.2支护系统安全系数[21]
(36)
式中,Q2—围岩稳定安全系数;Peq—初期支护与围岩变形平衡时的支护力。
3.5.3变形控制率
引用变形控制率[31](Ψ)来反映初期支护的支护效果,Ψ越大,表示支护结构对于围岩的变形控制效果越好:
(37)
式中,Ψ—初期支护结构对围岩的变形控制率;ulim—无支护时围岩发生的最大位移;ueq—施作初期支护后,围岩最终的稳定位移。
4 纵向变形曲线
Vlachopoulos[32]对满足弹塑性模型的围岩,建立了以最大塑性区半径Rmax为基础的隧道纵向变形曲线:
(38)
式中,l—隧道断面至掌子面的距离;Rmax—最大塑性区半径;u*—掌子面处的位移释放系数;umax—隧道围岩无支护状态下的最大位移。
利用GRC、SCC和LDP进行初期支护结构设计的步骤:
(1)结合式(13)、(18)和(21),利用Matlab等软件绘制出GRC;
(2)利用式(17)得到Rmax,再将Rmax、l代入式(38),得到u0;
(3)利用式(33)绘制出刚度为K的SCC;
(4)通过式(35)—(37)求得Q1、Q2和Ψ。若Q1、Q2大于1,则说明围岩处于稳定状态,且支护系统有一定的安全储备,设计合理;若Q1、Q2小于1,则说明在围岩支护系统会发生破坏,需要对l及K进行调整,重复步骤b~d,直至Q1、Q2和Ψ取得最优值。
GRC、SCC和LDP的对应关系如图4所示。
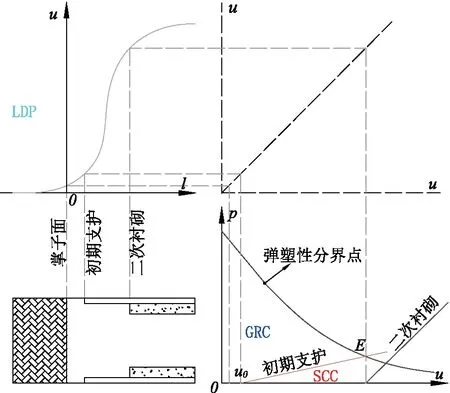
图4 GRC、SCC和LDP关系图
5 参数分析
为定性探明围岩级别、隧道埋深和隧道洞径对围岩特征曲线的影响,现取3种工况进行分析,见表2。围岩级别参数均取自2018版公路隧道设计规范[33]。
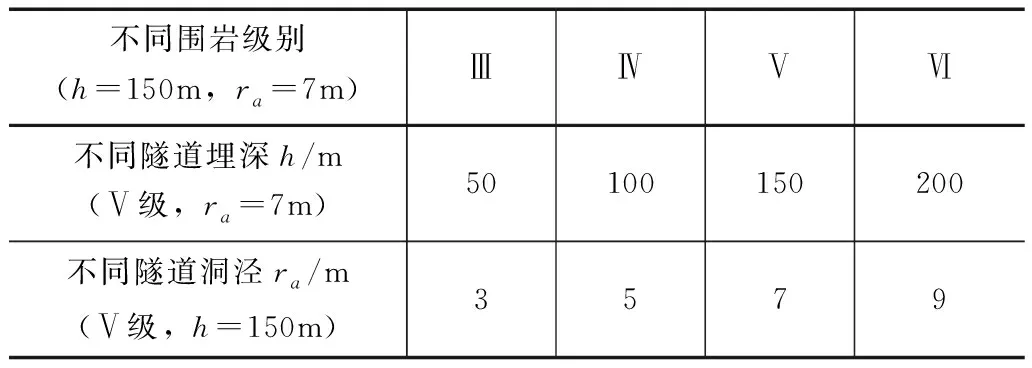
表2 不同工况参数表
5.1 不同围岩级别对GRC的影响
不同围岩级别下的GRC对比如图5所示。由图5可知,该工况下,整体上围岩级别越高,隧道围岩初始应力越低,但随着位移的逐渐释放,所需支护力随之增大。这是因为:围岩级别越高,其主要工程地质特征、岩石坚硬程度、岩体完整程度等岩性特征均越差;在原始应力状态时,岩性差的地层应力得到了一定释放,导致其初始应力较低,但围岩位移逐渐释放之后,此类围岩所能提供的自承载能力越差,需要及时提供足够刚度和极限承载能力的支护结构予以支撑。从图5还可以看出,对于岩性特征较好的Ⅲ级围岩,其最大位移为7.6mm,处于允许极限位移规范值[34]以内(此处为14mm),表示在该工况下无需施作支护,围岩依靠自承载能力即能达到自稳。

图5 不同围岩级别下的GRC对比图
5.2 不同隧道埋深对GRC的影响
不同隧道埋深下的GRC对比如图6所示。该工况下,选择的是Ⅴ级围岩,岩性较差。由图6可知,隧道埋深对围岩特征曲线的影响比较明显。随着隧道埋深的增加,表现为初始地应力愈大。在埋深较大的情况下,围岩的塑性变形愈大,其弹性变形所占比例愈小,此时若要维持隧道围岩在弹性阶段,需要提供较大刚度和约束压力。但若允许围岩发生一定位移释放后,其围岩自身塑性变形所承担的围岩压力增大,同时所需的支护压力明显减小。在此类围岩中施作柔性支护的重要原因,就是依靠柔性支护既能使围岩变形得到有效控制,又能使围岩位移得到一定释放,充分

图6 不同隧道埋深下的GRC对比图
发挥围岩自身的承载能力,更好地调节岩体和支护结构的应力、应变状态,最大化减小支护结构所需提供的阻力。
5.3 不同隧道洞径对GRC的影响
不同隧道洞径下的GRC对比如图7所示。由图7可知,该工况下,围岩初始应力均相同,但随着隧道洞径的增大,其围岩塑性变形逐渐增大。这是因为:由式(17)可知,洞径愈大,围岩塑性区半径愈大,对地层的影响范围愈广。
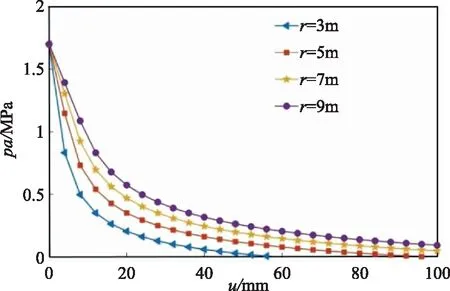
图7 不同隧道洞径下的GRC对比图
6 典例分析
昭通至泸州高速公路彝良至镇雄段白岩脚隧道,隧道全长左幅5265m,右幅5245m,最大埋深470m。隧道区地形较为陡峻,属构造侵蚀中山地貌区,围岩以强风化白云岩为主,部分为中分化。选取典型里程段左幅ZK20+860~ZK21+000段和ZK25+200~ZK25+300段进行隧道初期支护设计验证,左幅地质纵断面如图8所示。根据地质勘探资料,ZK20+860~ZK21+000段为Ⅴ1围岩,最大埋深190m,支护结构横断面如图10所示;ZK25+200~ZK25+300段为Ⅳ1围岩,最大埋深200m,支护结构横断面如图9所示。根据公路隧道设计规范,Ⅴ1围岩和Ⅳ1围岩均取规范值[33],其物理参数如表3所示。有学者认为[34],基于弹塑性原理分析下的隧道围岩位移偏于保守,故隧道周边允许相对位移值依据规范[35],并结合岩性特征,Ⅳ1围岩允许相对位移值按Ⅲ级围岩取为0.2%;Ⅴ1围岩按Ⅳ级围岩取为0.4%。因Ⅳ围岩断面隧道宽12m,Ⅴ围岩宽12.5m,故隧道周边极限位移值Ⅳ围岩为24mm,Ⅴ围岩为50mm。
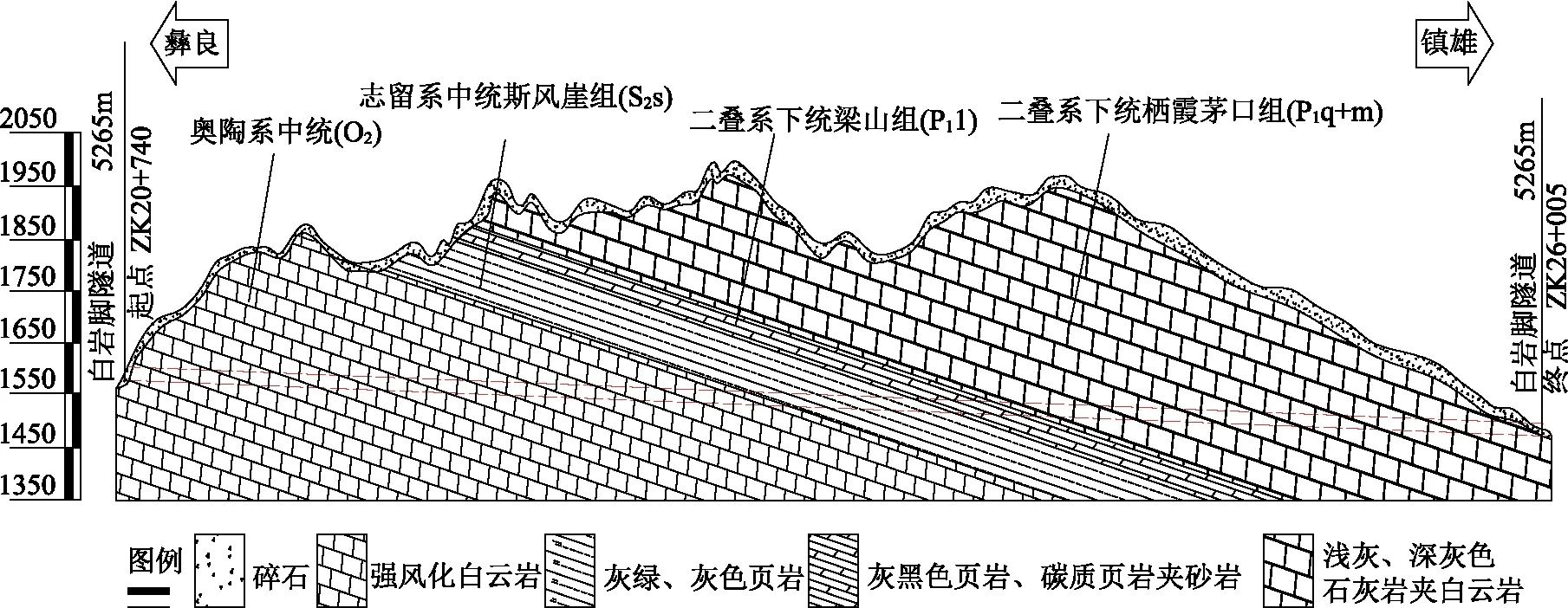
图8 白岩脚隧道左线地质纵断面示意图
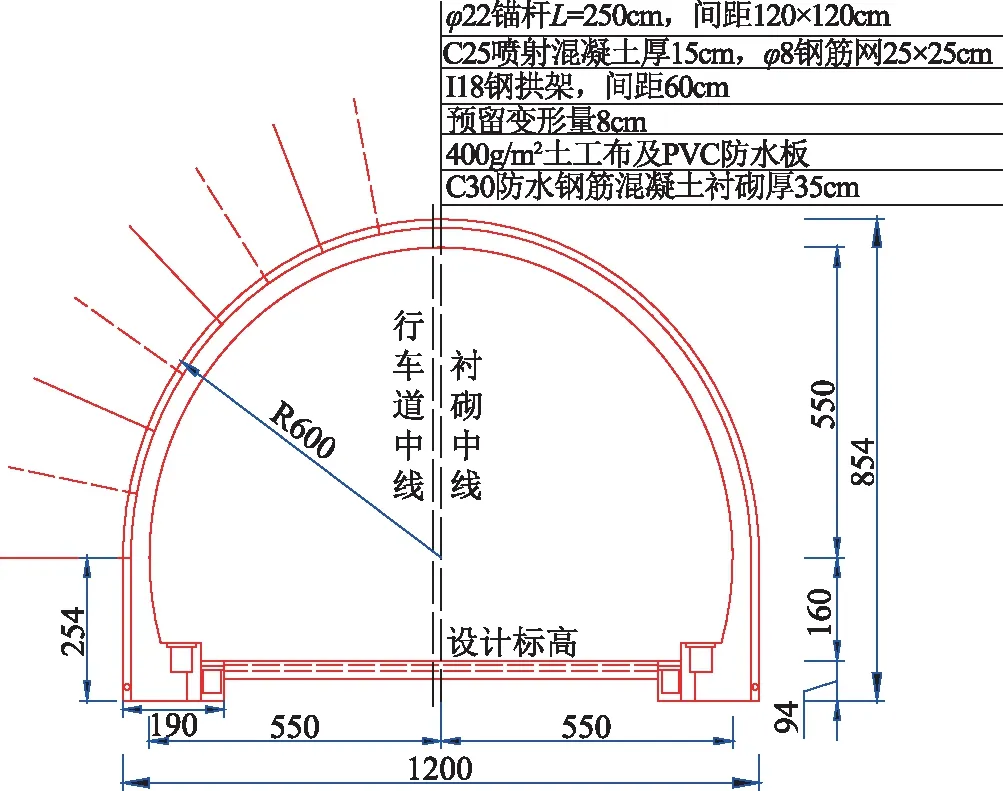
图9 ZK25+200~300段支护结构横断面图(单位:cm)
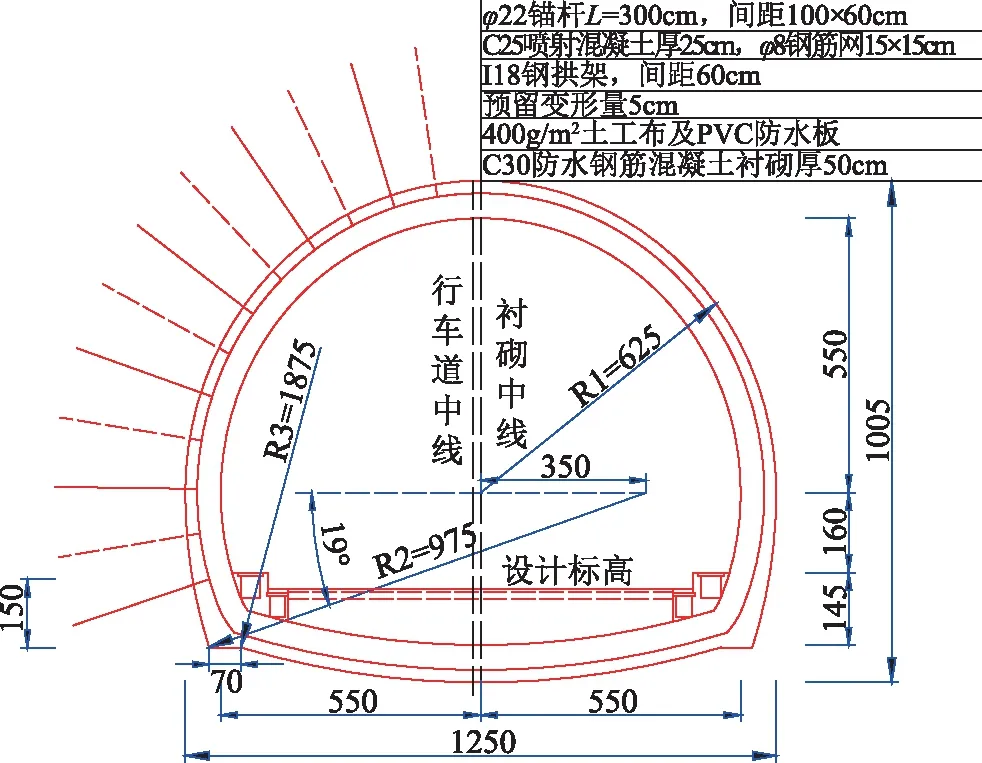
图10 ZK20+860~21+000段支护结构横断面图(单位:cm)
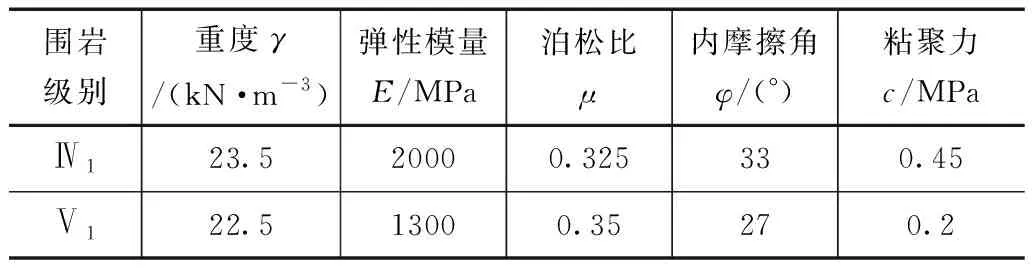
表3 Ⅳ1、Ⅴ1级围岩物理力学参数
6.1 ZK25+200~300段
该段隧道断面面积S=87.03m2,通过式(22)可得其等代圆半径为5.79m。根据其初期支护参数,C25喷射混凝土弹性模量Ec=2.8×104MPa,抗压强度25.1MPa,厚度为15cm,泊松比为0.2。φ22锚杆弹性模量E=210×103MPa,长度为l=250cm,间距120cm×120cm,破坏荷载Qbf=196kN,锚固端和锚固头的荷载-变形常数η=4.2×10-5m/kN。
代入式(23)—(28)得:
Kc=133.082MPa/m,Pmax,c=0.650MPa,ulim,c=4.89mm。Kb=9.472MPa/m,Pmax,b=0.136MPa,ulim,b=14.37mm。由式(32)、(33)得组合支护系统刚度K=142.554MPa/m,最大支护阻力Pmax=0.6966MPa。
利用围岩稳定安全系数(Q1)、初期支护安全系数(Q2)和围岩变形控制率(Ψ)三者对开始施作初期支护的距离进行综合评价。在分别距离掌子面0、1、2、3、4、5m处开始施作初期支护,其围岩及支护系统安全系数如图11所示。
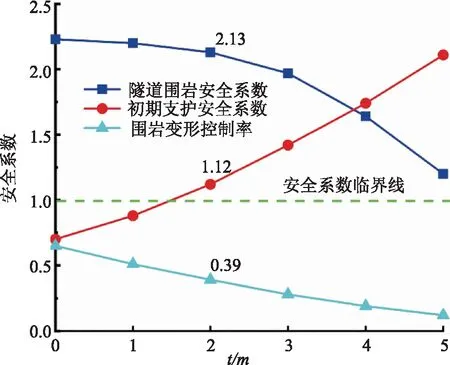
图11 不同支护起点对应Q1、Q2、Ψ
由图11可知,在0m及1m处,Q2小于1,即在安全系数临界值以下,表示其支护系统在隧道稳定之前即达到了其支护阻力极限值,发生了破坏。2m以后,在平衡时支护系统有了安全盈余,但Q1和Ψ均逐渐降低,故选择在距离掌子面2m处开始施作初期支护。此时,该段隧道围岩特征曲线及支护结构特征曲线如图12所示。
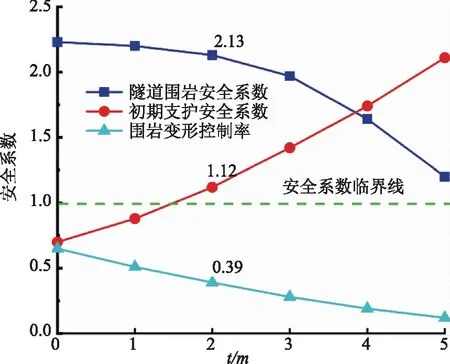
图12 ZK25+200~300段收敛-约束曲线
由图12可知,此时Q1=2.13,Q2=1.12,Ψ=0.39,围岩处于较安全的状态,初期支护系统亦有一定的安全盈余,说明初期支护起点距离掌子面2m是合理的。
6.2 ZK20+860~21+000段
该段隧道断面面积S=103.83m2,通过式(22)可得其等代圆半径为6.32m。根据其初期支护参数,C25喷射混凝土厚度为25cm;φ22锚杆,长度为300cm,间距100cm×60cm,喷射混凝土及锚杆其它参数同第6.1节。I18钢拱架弹性模量E=210×103MPa,横截面面积30.756cm2,横截面高度h=18cm,间距60cm,屈服强度σs=268MPa。
代入式(23)—(31)得:
Kc=187.829MPa/m,Pmax,c=0.992MPa,ulim,c=5.28mm;Kb=20.943MPa/m,Pmax,b=0.327MPa,ulim,b=14.37mm;Ks=27.701MPa/m,Pmax,b=0.220MPa,ulim,b=7.96mm;由式(32)、(33)得组合支护系统刚度K=236.472MPa/m,最大支护阻力Pmax=1.249MPa。
同第6.1节,在分别距离掌子面0、1、2、3、4、5m处开始施作初期支护,其围岩及支护系统安全系数如图13所示。
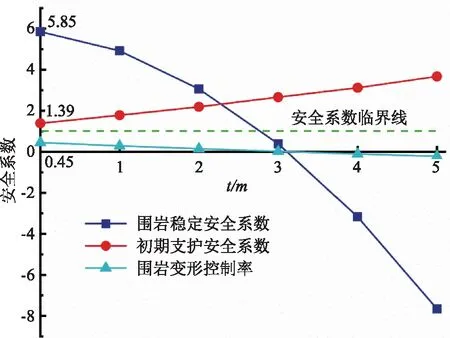
图13 不同支护起点对应Q1、Q2、Ψ
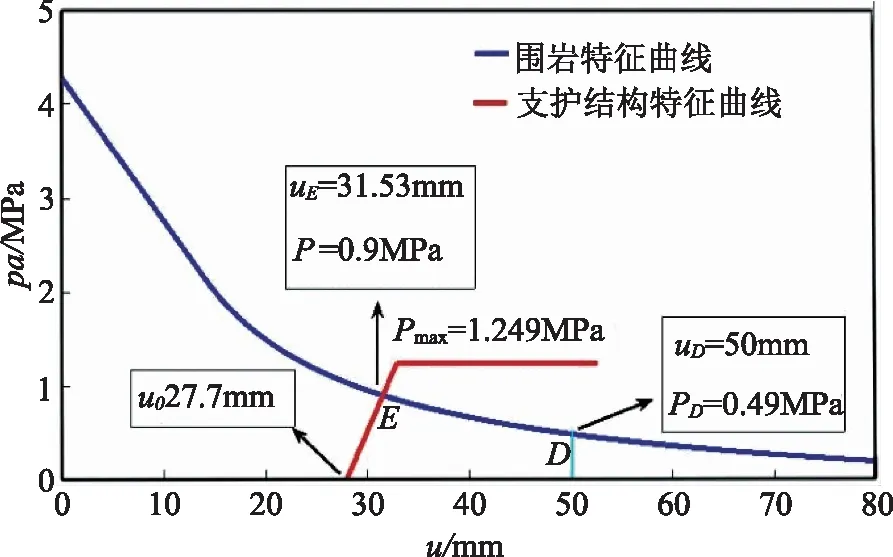
图14 ZK20+860~21+000段收敛-约束曲线
由图13可知,Q2逐渐增大,且在0m处,Q2即大于1,表示在掌子面处施作支护系统时,隧道稳定后支护结构亦有一定的安全盈余。Q1和Ψ均逐渐降低,在l=3m时,Q1突破了安全系数临界线,此时隧道围岩已经达到允许极限位移值,已经失稳。考虑新奥法“少扰动,早支护,勤量测,紧封闭”的施工原则,故选择在掌子面处即开始施作初期支护。此时,该段隧道围岩特征曲线及支护结构特征曲线如图14。
由图14可知,此时Q1=5.85,Q2=1.39,Ψ=0.45,围岩处于较安全的状态,初期支护系统亦有一定的安全储备,说明在掌子面处施作初期支护是可行的。
7 结论
(1)本文基于弹塑性模型推导了深埋圆形隧道的围岩特征曲线解析式,并结合“当量半径法”得到了非圆形断面隧道的等价圆半径,实现了非圆形隧道荷载-位移关系曲线的转化求解。
(2)利用GRC、SCC和LDP的对应关系,给出了初期支护结构设计的步骤,可为隧道初期支护设计提供指导。
(3)引入围岩稳定安全系数、支护结构安全系数和围岩变形控制率,对初期支护结构的合理支护起点的选择进行综合评价。
(4)定性分析了围岩级别、隧道埋深和隧道洞径对围岩特征曲线的影响。发现围岩所需支护力与围岩级别呈正比,而初始地应力与围岩级别呈反比;隧道埋深对围岩特征曲线的影响较明显;隧道洞径愈大,围岩塑性区愈广,塑性变形愈大。
(5)利用文章理论成果对白岩脚隧道初期支护结构的合理支护起点进行了选择分析。发现对于ZK25+200~300段,合理支护起点是距离掌子面2m处,此时Q1=2.13,Q2=1.12,Ψ=0.39,围岩处于较安全的状态;对于ZK20+740~850段,合理支护起点就是掌子面处,此时Q1=5.85,Q2=1.39,Ψ=0.45,围岩处于较安全的状态,且初期支护系统亦有一定的安全储备。
(6)将喷射混凝土、锚杆和钢拱架等单元刚度简单叠加作为组合支护结构刚度,存在一定的误差,后续研究需进一步优化。

