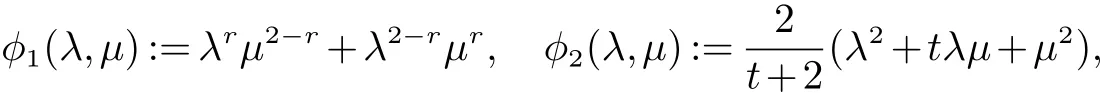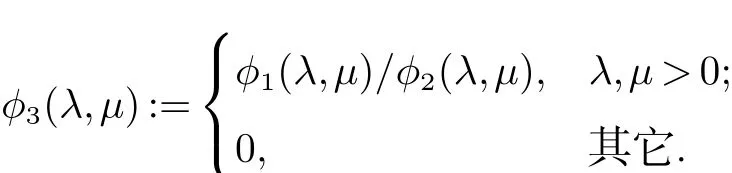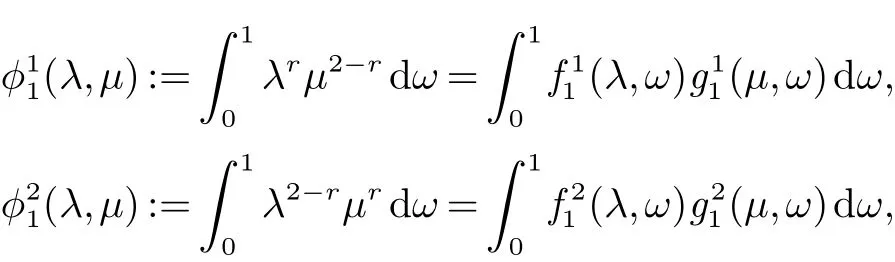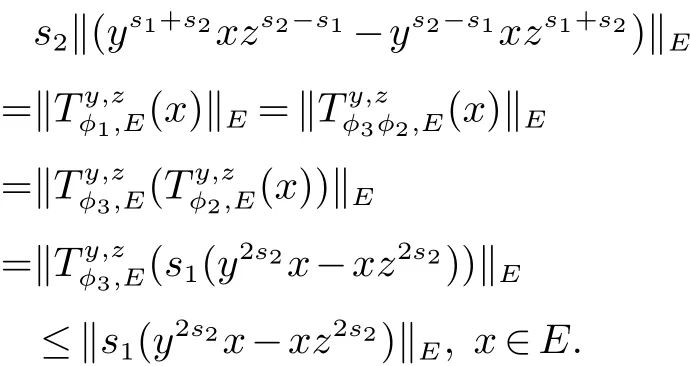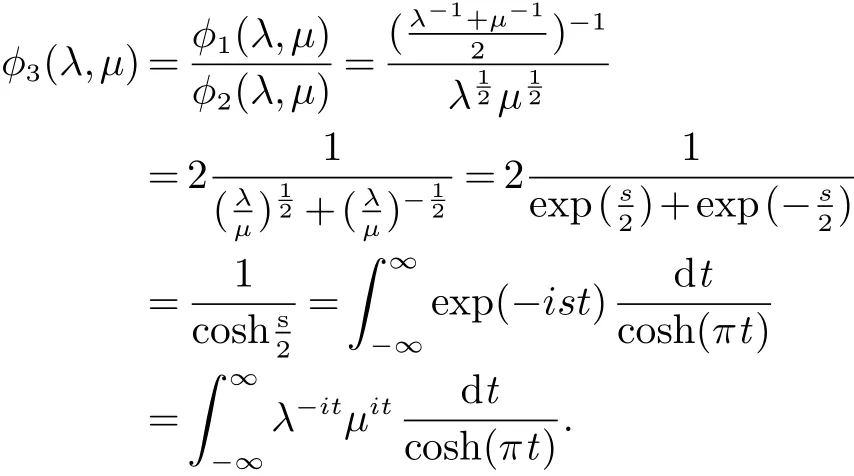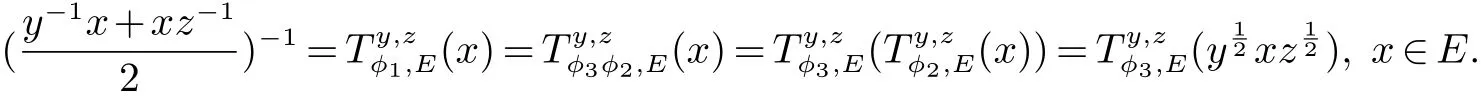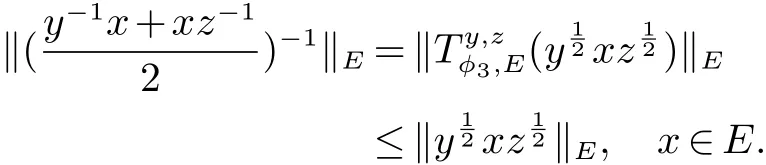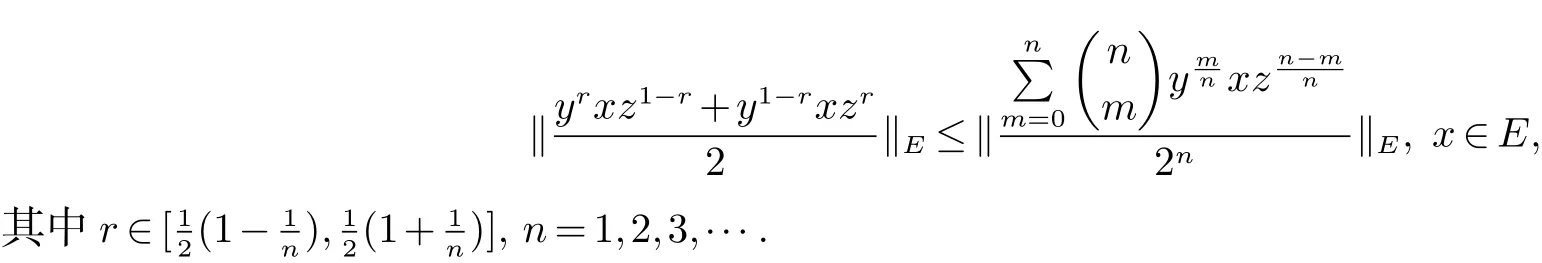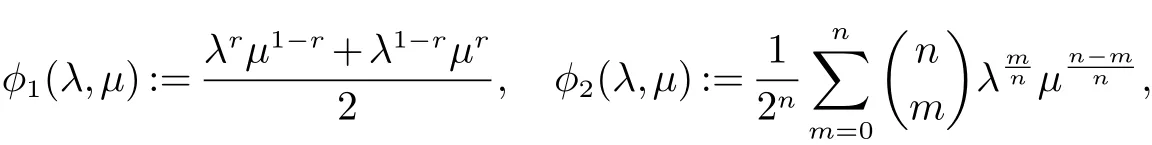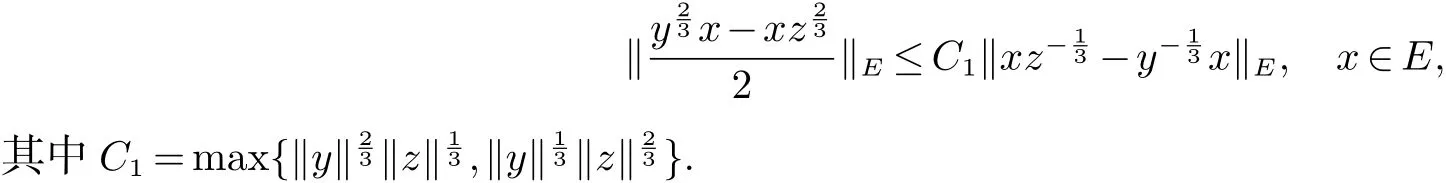与可测算子相关的广义Heinz 不等式∗
李宝珍,韩亚洲,2†
(1. 新疆大学数学与系统科学学院,新疆乌鲁木齐 830017;2. 太原理工大学数学学院,山西太原 030024)
0 引言
我们用Mn表示n×n 阶复矩阵构成的集合.称Mn上的范数‖·‖u为酉不变范数,如果对任意的A ∈Mn,酉矩阵 U,V ∈Mn, 有 ‖UAV ‖u=‖A‖u.
算子范数形式的Heinz 不等式最早是由Heinz 在文献[1]中给出的. 此后,Heinz 不等式引起了许多学者的关注. 1993 年, Bhatia 与Davis 在文献[2]中得到了酉不变范数形式的Heinz 不等式

其中0 ≤r ≤1,A,B,X ∈Mn且A,B 是半正定矩阵. 随后, Zhan 在文献[3]中证明了含有参数的Heinz 不等式

2016 年,Kosaki 在文献[4]中把Heinz 不等式做了如下推广

最近, Dodds 等在文献[5]中把Heinz 不等式推广到了可测算子的形式, 并给出了一些τ-可测算子的Heinz型次优化不等式.
本文应用文献[5-6]中的方法给出了τ-可测算子的广义Heinz 型次优化不等式, 并把上述不等式(2)和(3)推广到了τ-可测算子的情形.
1 准备知识
本文中M 表示可分希尔伯特空间H 上的具有正规忠实半有限迹τ 的半有限von Neumann 代数. M+表示M 的全体正元构成的锥. 1 表示M 中的单位算子, P(M)表示M 中所有正交投影构成的格. M′表示M 的交换子, 记 M′={x ∈B(H):xy=yx,∀y ∈M}.
称x 附属于M, 若对M′中的任意一个酉元u, 有ux=xu, 其中x:D(x)→H 上的闭稠定线性算子. 称附属于M 的算子 x 关于 τ 可测, 如果对任意的 ε>0, 存在 e ∈P(M), 使得 e(H)⊂D(x)且 τ(e⊥)≤ ε. L0(M)表示可测算子全体构成的集合.
设x ∈L0(M), 对于任意的t>0, 我们定义广义奇异值µt(x)为
设 x,y ∈L0(M), 我们称y 次优化于x, 若对所有的t ≥0 都满足

在这篇文章中, 我们通常记作x ≺≺y, 或µ(x)≺≺µ(y).
设 E 是 L0(M)的线性子空间, ‖·‖E是它的范数. 我们称 ‖·‖E为对称范数, 如果 x ∈ E, y ∈ L0(M)且µ(y)≤ µ(x)使得 y ∈ E 和 ‖y‖E≤ ‖x‖E. 我们称 ‖·‖E为完全对称范数, 如果 E 是对称范数并满足下列条件: 若x ∈E, y ∈L0(M)且 y ≺≺x,则 y ∈E,‖y‖E≤‖x‖E. 如果 E ⊆L0(M)依完全对称范数 ‖·‖E成为 Banach 空间,我们称 E 为完全对称算子空间. 特别的, 非交换 Lp空间 Lp(M)={x ∈L0(M):‖x‖p=(τ(|x|p))1p<∞}(0 设y,z ∈L0(M)是自伴的. 我们介绍一种特殊的函数类A, 设 为Borel 函数, Spec(y),Spec(z)分别为y,z 的谱集. 称φ ∈A, 若存在一个σ-有限的测度空间(Ω,Σ,m)使得 其中 是有界B(R)×Ω 可测复值函数并且 定义1 设y,z ∈L0(M)是自伴算子, φ ∈A. 定义双重积分算子Ty,zφ,∞:M →M 为 其中上述积分在弱*拓扑意义下存在, 即对任意的a ∈L1(M), 由文献[5]中的定理4.5 可知, 上述定义是合理的, 并且双重积分算子Ty,zφ,∞(x)不依赖于φ 的表达式. 定义2 设y,z ∈L0(M) 自伴且φ ∈A. 定义双重积分算子Ty,zφ,1:L1(M)→L1(M) 为Ty,zφ,∞到L1(M)∩M 的限制的唯一延拓(见文献[5]中定义4.10). 而且定义双重积分算子Ty,zφ,+:L1(M)+M →L1(M)+M 为 由于Ty,zφ,1(x)=Ty,zφ,∞(x),x ∈L1(M)∩M, 所以上述定义是合理的. 定义3 设0 ≤y,z ∈L0(M) 且φ ∈A. 若E 是完全对称算子空间, 则定义双重积分算子 Ty,zφ,E:E →E 是双重积分算子Ty,zφ,+:L1(M)+M →L1(M)+M 在E 中的限制. 设 0 ≤y,z ∈L0(M), φ ∈A 且 E 是完全对称算子空间. 如果 f:Spec(y)→C,g:Spec(z)→ C 是有界 Borel 函数,φ(λ,µ)=f(λ)g(µ),(λ,µ)∈Spec(y)×Spec(z), 因此 此外, 如果 φ1,φ2∈A, 0 ≤y,z ∈L0(M)且 E 是完全对称算子空间, 容易证明 本文的主要结果证明中不但要用到上述双重积分算子的性质, 还将用到如下引理. 引理 1[5]设 0 ≤y,z ∈L0(M) 且 φ ∈A. 则对任意的 x ∈L1(M)+M, 有 如果E ⊆L0(M)是一个完全对称算子空间, 称E ⊆L1(M)+M. 由此可知对任意的x ∈E, 有 其中 m 是一个σ-有限测度. 关于双重算子积分的基本性质与具体知识参见文献[5, 8]. 在下面的证明过程中我们还将用到著名的Bochner 定理(见文献[9]), 首先我们回顾一下正定函数的定义. 定义 4 我们称函数 f:R → C 为正定函数, 若对任意的 x1,x2,···,xs∈ R 和 c1,c2,···,cs∈ C 满足 引理2(Bochner’s 定理) 若f:R →C 为一个连续的正定函数, 则存在R 上的正有限测度m 使得 定理1 设E ⊆L0(M)是一个完全对称算子空间且y,z 为M 中的可逆正算子. 如果r ∈[0,1]且t ∈(−2,0],则 证明 设 且 首先证明 φ1,φ2且 φ3属于 A. 因为 y,z 为 M中的可逆正算子, 所以存在 ε > 0, 使得 Spec(y) ∈ [ε,‖y‖] 且 记 则 进而应用 (4)和 (5)可知, φ11, φ21∈A. 再结合文献 [5]中的引理 4.6, 可得 φ1∈A. 类似地可以证明 φ2∈A. 且 因此φ3∈A. 进而结合引理1 与(6),(7)可得, 对于任意 故, 定理2 设y,z 为M 中的可逆正算子且E ⊆L0(M)是一个完全对称算子空间. 若s1,s2∈R 且满足0<|s1|≤|s2|, 则对x ∈ E, 有 证明 设 且 此定理的证明与定理1 类似, 所以我们仅对φ3∈A 的情形加以证明. 因为y,z 为M 中的可逆正算子, 所以存在可知 定理3 设E ⊆L0(M)是一个完全对称算子空间,y,z 为M 中的可逆正算子. 则 证明 设 且 此定理的证明方法与定理1 的证明类似, 为了阅读方便我们给出完整的证明过程. 由φ2的定义可知φ2∈A 显然成立. 下证 φ3∈A. 因为 y,z 为 M 中的可逆正算子, 所以存在 ε>0 使得 Spec(y)∈[ε,‖y‖]且 Spec(z)∈[ε,‖z‖].设 λ ∈Spec(y),µ ∈Spec(z), 令 因为 且 从而 定理4 设E ⊆L0(M)是完全对称算子空间且y,z 为M 中的可逆正算子, 则 证明 此定理的证明方法与定理1 类似, 其中 且 由定理1 的证明方法可知,只需证明φ3∈A 即可.因为y,z 为M 中的可逆正算子,所以存在ε>0 使得Spec(y)∈7.3 可知 因为φ3(λ,µ)满足文献[4]中定理6 的条件, 因此存在R 上的一个概率测度m 使得 且 从而,φ3∈A. 定理5 设E ⊆L0(M)是完全对称算子空间. 如果y,z 为M 中的可逆正算子, 则 证明 设 且 由定理1 中的证明可得φ1,φ2∈A. 我们只需证明φ3∈A 即可. 因为y,z 为M 中的可逆正算子, 所以存在ε>0使得 Spec(y)∈[ε,‖y‖] 且 Spec(z)∈[ε,‖z‖]. 设 λ ∈Spec(y),µ∈Spec(z), 令 由于



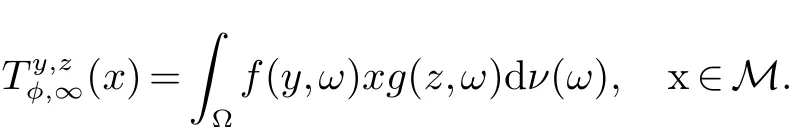
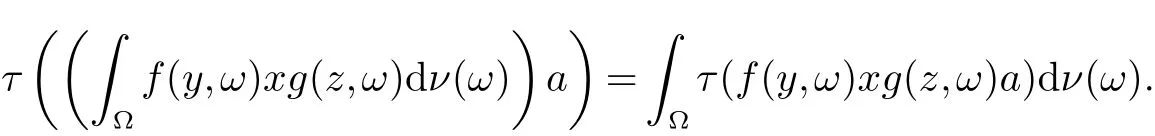








2 主要结论