基于金枪鱼群优化算法的Jensen模型参数求解
薛萍,刘玲*,王仰仁,孙书洪
基于金枪鱼群优化算法的Jensen模型参数求解
薛萍1,刘玲1*,王仰仁2,孙书洪2
(1.天津农学院 计算机与信息工程学院,天津 300384;2.天津农学院 水利工程学院,天津 300384)
【目的】利用智能优化算法求解Jensen模型参数。【方法】将分布估计引入金枪鱼群优化算法(TSO)中,形成基于分布估计的金枪鱼群优化算法(ITSO)。将改进的基于分布估计的金枪鱼群优化算法(ITSO)与其他算法在CEC2017测试集上进行性能验证,并利用山西潇河灌溉试验站非充分灌溉试验结果对该算法与其他方法求解的精准性进行对比。【结果】①在CEC2017测试集上,对比ITSO、TSO、GWO、WOA、SSA和BOA共6种算法的寻优性能表明,ITSO算法寻优能力最强。②在山西潇河灌溉试验站非充分灌溉试验结果上分别将ITSO与SPSS软件中非线性回归分析、TSO计算得出的结果进行对比,平均相对误差分别为7.79%、8.13%和7.79%。TSO算法经过50次迭代后找到最优解,而ITSO算法仅需35次迭代后找到最优解。【结论】基于分布估计的金枪鱼群优化算法(ITSO)求解Jensen模型参数,拟合精度高且寻优速度快。
水分生产函数;Jensen模型;模型参数求解;分布估计;金枪鱼群优化算法
0 引言
【研究意义】作物产量与水分因子之间的数学关系称为作物水分生产函数,是作物生产模型中联系水分和生产力因素的关键[1],可为非充分灌溉优化决策提供科学依据。【研究进展】作物水分生产函数模型有很多种,其中Jensen模型在拟合效果和模型结构方面具有优势,已被广泛应用[2-3]。影响Jensen模型预测精度的关键参数是水分敏感指数,学者们对水分敏感指数的精确求解做了大量的尝试。王喜芹等[4]采用SPSS中非线性回归分析计算Jensen模型参数,操作简单,只需要输入相关数据即可得出Jensen模型的水分敏感指数。郑文超等[5]将单纯形算法与基于群体的微粒群算法相结合,提出了基于单纯形微粒群优化算法(SMPSO),应用于求解作物水分生产函数Jensen模型参数中,该方法可以简单有效的求解Jensen模型参数。朱伟峰等[6]用自由搜索算法来率定Jensen模型水分敏感指数,自由搜索算法可以直接率定模型的水分敏感指数,在一定程度上改善了Jensen模型的适用性。由于灌溉试验处理的组数多且影响作物产量因素有很多种,仍然存在模型参数求解精度不高的问题。
智能算法近年来发展迅速,很多学者受生物种群社会性或自然界现象规律的启示,发明了很多用于解决复杂优化问题的智能算法。金枪鱼群优化算法(Tuna swarm optimization,TSO)[7]的灵感来源于金枪鱼群的2种群体觅食行为,具有调整参数少、计算简单等优点。【切入点】但与其他智能优化算法类似,存在收敛精度不高等问题。【拟解决的关键问题】为此,本文引进一种新的智能算法,将分布估计算法引入到金枪鱼群优化算法中,形成基于分布估计的金枪鱼群优化算法(ITSO),可为Jensen模型参数求解提供一种新的精确途径。
1 Jensen模型参数的金枪鱼群优化算法
1.1 Jensen模型的表达式
目前作物水分生产函数中生育阶段模型应用较多,生育阶段模型分为2类,一类是加法模型,一类是乘法模型[8]。其中常见的加法模型有Stewart、Blank、Singh模型等,最常用的乘法模型是Jensen模型[9-10]。Jensen模型相较于其他模型结构更为合理,在一定程度上可以反映出作物在不同生育阶段水分胁迫对作物产量的影响。Jensen模型常用的表达式为:


1.2 分布估计算法(Estimation of distribution algorithm,EDA)
分布估计算法的概念最早在1996年被提出,本质上是一种基于概率模型的新型优化算法,即通过一个概率模型在空间中表示出候选解的分布情况,采用统计学习手段从群体的宏观角度建立候选解分布的概率模型,随机采样产生新的种群[11];反复进行,实现种群的进化,直到终止。EDA能够降低时间的复杂性,估计种群的进化方向,同时具备更快的收敛速度和更强的全局搜索能力。
加权协方差矩阵是EDA算法的核心构成[12]。基于加权协方差矩阵的高斯分布估计计算式为:
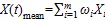


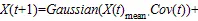
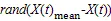
式中:为有希望的种群;1,2, …,为按照适应度值从高到低排列的个有希望的解决方法;()则是X的加权协方差矩阵;(+1)是更新后的位置。EDA由于局部搜索能力弱,迭代后期易陷入局部收敛[13],所以目前采用的模型仍有不足。
1.3 金枪鱼群优化算法(Tuna swarm optimization,TSO)
TSO算法是根据金枪鱼觅食行为而衍生的一种基于群的元启发式全局优化算法[7],其算法结构简单,需要调整的参数少,易于实现。TSO通过在D维搜索空间中随机产生个金枪鱼个体组成初始种群:
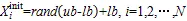
式中:Xinit为初始化的第个金枪鱼个体位置;为在(0,1)范围内均匀分布的随机向量;和为搜索空间的上、下边界;为金枪鱼种群的数量。
当目标难以锁定时,金枪鱼就会以密集的螺旋式阵型进行追捕。在追捕猎物的同时,金枪鱼群之间还会交换信息,实现相邻个体之间的信息共享。螺旋式觅食位置更新计算式为:
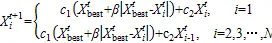
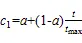
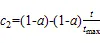
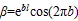

式中:X1为第1次迭代的个体位置;best为当前最佳个体位置;1和2为权重系数;表示当前迭代的次数;max表示最大迭代次数;为一个在(0,1)范围内的随机数。
当最优个体无法找到食物时,在搜索空间中随机生成一个坐标作为螺旋式觅食的参考点。
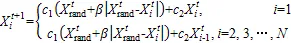
式中:Xrand表示在搜索空间中随机生成的坐标点。
金枪鱼除了螺旋式觅食之外,还有抛物线型觅食。位置更新计算式为:
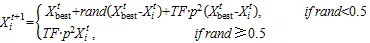
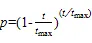
式中:表示一个值为1或-1的随机数。
TSO算法在整个优化的过程中,会不断地更新和计算直到满足最终条件。但和其他智能优化算法类似,存在收敛精度不高等问题。
1.4 基于分布估计的金枪鱼群算法
由于EDA算法和TSO算法属于不同类型的进化算法,且都易于与其他智能优化算法相结合,以提高算法的性能。故将高斯分布估计方式替换TSO抛物线策略,以克服TSO算法中的缺陷。每个个体都可以使用高斯分布估计方法来根据个体情况来更新其位置,形成基于分布估计的金枪鱼群算法ITSO。ITSO算法的具体流程如下:
步骤1:算法参数设定。初始化设置种群数,最大迭代次数max,待优化参数维度等。
步骤2:种群初始化。在搜索空间内随机产生一组初始化种群(),=1,2,…,,种群内每个个体代表待优化问题的1个可行解。
步骤3:计算适应度值。根据个体所处位置分别计算个体的适应度(X)。
步骤4:更新参数1、2、、。
步骤5:位置更新。根据式(5)、式(6)、式(7)、式(12)更新个体位置。
步骤6:迭代计算。返回步骤3计算个体适应度值。
步骤7:算法结束。检查是否满足终止条件,若满足,则输出最优个体位置和对应适应度值;否则,返回步骤3。
2 仿真试验与结果分析
2.1 算法性能测试
为了测试ITSO算法的性能,使用CEC2017[14]中的29个测试函数进行测试,并将其与鲸鱼优化算法(whale optimization algorithm, WOA)[15]、麻雀搜索算法(sparrow search algorithm, SSA)[16]、灰狼优化算法(grey wolf optimizer, GWO)[17]、蝴蝶优化算法(butterfly optimization algorithm, BOA)[18]以及传统的TSO[7]算法进行比较分析。CEC2017中29个测试函数都是作为最小化问题进行评估[14],其中分为2个单峰测试函数(F1~F2)、7个多峰测试函数(F3~F9)、10个混合函数(F10~F19)、10个复合函数(F20~F29)。为了公平比较,所有测试函数解维度为30,设置种群规模为30,搜索空间全部为[-100,100],所有算法分别在每个测试函数上独立运行30次,每次运行的最大迭代数为1 000,对比算法的实验参数设置与原文献保持一致。
本文分别统计了WOA、SSA、GWO、BOA、TSO和ITSO算法在29个测试函数上独立运行30次结果的排名均值,分别为4.31、5.03、2.21、5.48、2.10和1.86。鉴于篇幅原因,本文只给出了在CEC2017测试函数集上部分函数的测试排名结果(表1),即2个单峰函数F1和F2,2个多峰函数F4、F6,4个混合函数F10、F13、F15和F19,4个复合函数F21、F24、F26和F29。
从表1可以看出,在2个单峰测试函数(F1~F2)求解时,TSO算法和ITSO算法寻优结果相差不大,但都明显优于其余4种算法。在2个多峰测试函数(F4、F6)求解时,虽然GWO算法在2个测试函数上都取得了最优结果,但是根据6种算法在2个多峰测试函数上寻优平均排名情况来看,ITSO算法仅次于GWO算法。在10个混合函数(F10、F13、F15和F19)求解时,ITSO算法在3个测试函数上都取得了最优的结果。在4个复合函数(F21、F24、F26和F29)求解时,ITSO算法的寻优效果相对于GWO算法和TSO算法并不显著,但由综合均值和标准差可知ITSO算法寻优高且结果稳定。根据排名均值可以得出6种算法寻优性能高到低排序为:ITSO、TSO、GWO、WOA、SSA和BOA。
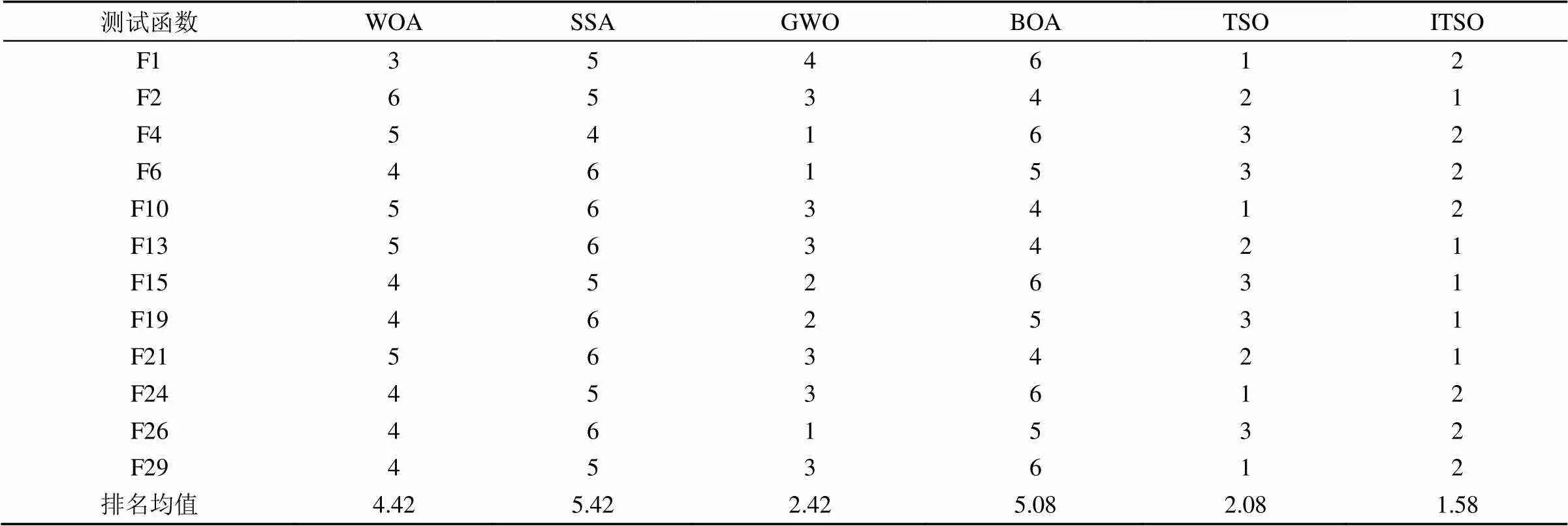
表1 算法结果排名
为了更加直观体现ITSO算法和其他对比算法收敛精度和收敛速度,本文绘制了29个测试函数的收敛曲线。鉴于篇幅原因,本文只给出了6种算法在4个测试函数上30次得到的平均收敛曲线图。图1为不同算法在测试函数上的收敛曲线。图1(a)为单峰测试函数收敛曲线,ITSO算法收敛精度最高;图1(b)为多峰测试函数收敛曲线,可以看出ITSO算法虽然后期收敛速度慢,但是从整体上来看稳定性居中,避免了早期收敛,有着良好的性能。
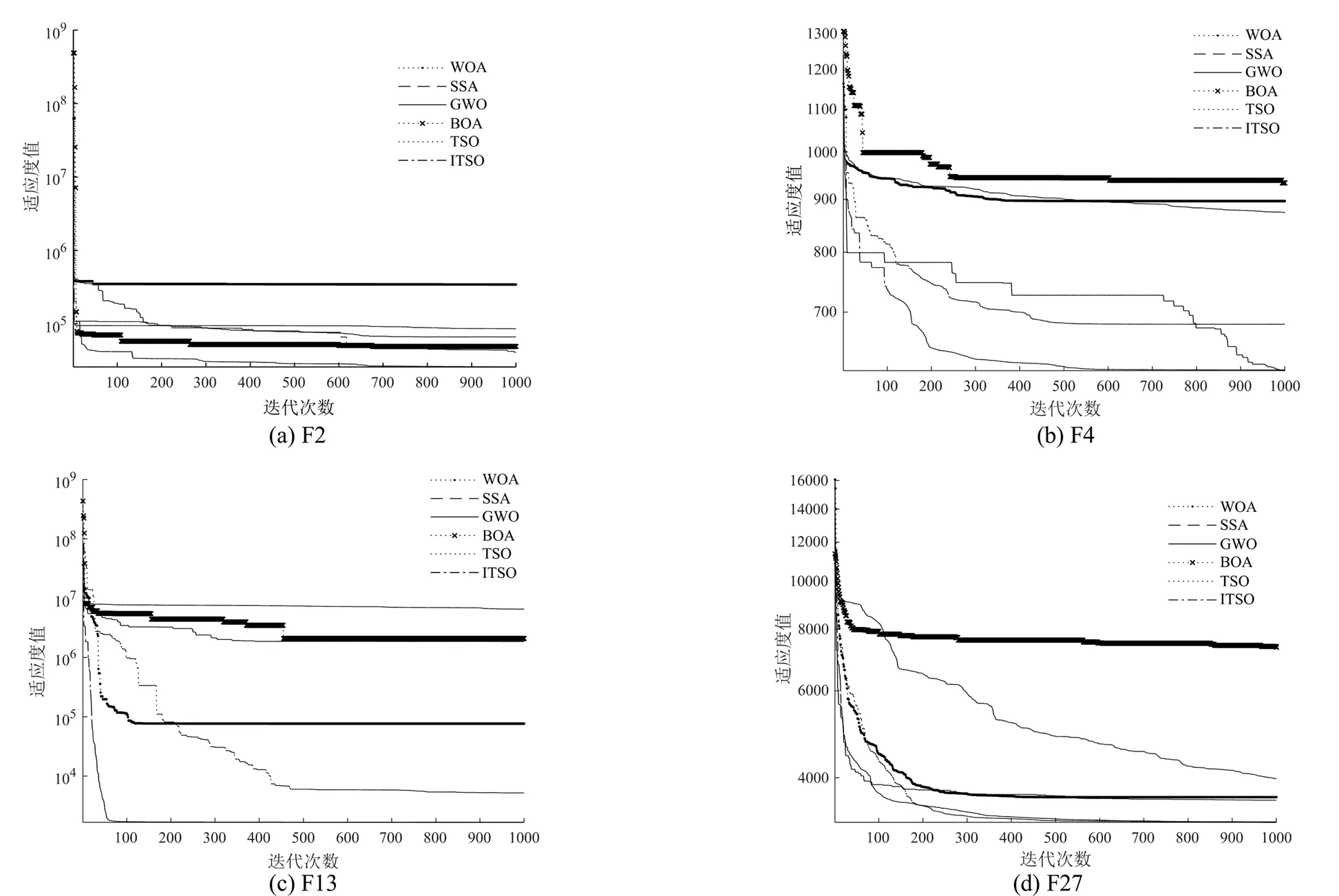
图1 不同算法在测试函数上的收敛曲线
图1(c)为混合测试函数收敛曲线,可以看出,ITSO算法可以有效的收敛到全局最优解;对于复合测试函数F27,ITSO算法和TSO算法收敛精度和收敛速度相差不大(图1(d))。综上,ITSO算法在求解4个测试函数时,其收敛精度和收敛速度均优于相比较的另外5种算法。
2.2 仿真计算与结果分析
由于TSO算法和ITSO算法原理相同,所以选取相同的适应度函数,依据式(1)即以计算的相对产量和实测的相对产量的相对误差之和作为适应度函数。
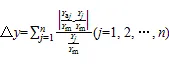
式中:为样本总数目;为样本编号;aj为第个样本所计算的产量;为第个样本实际的产量;m为全生育期不受旱条件下作物的最高产量。
选取潇河灌溉试验站1989—1990年和1992—1995年冬小麦水分生产试验数据为例,数据如表2所示。
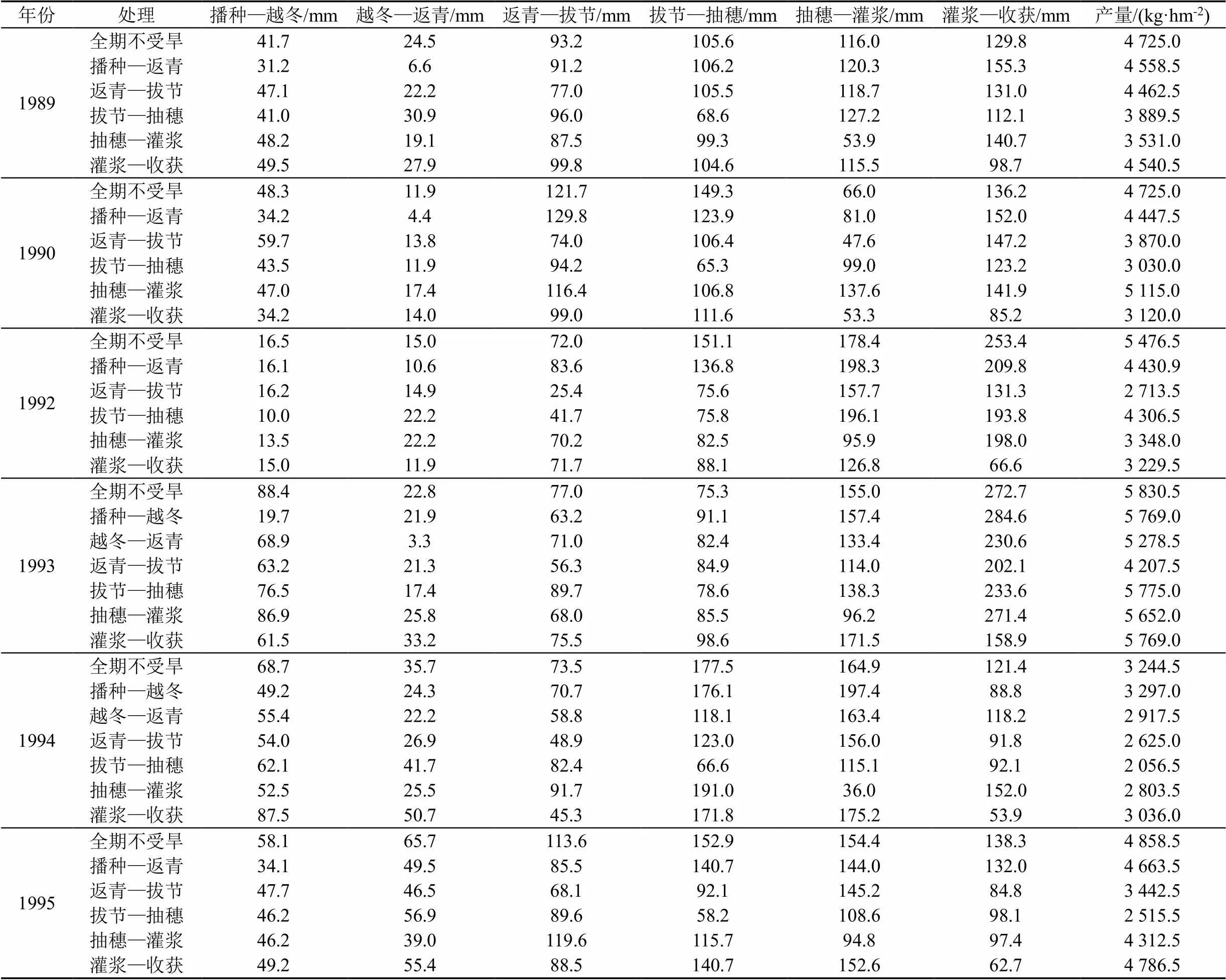
表2 山西潇河冬小麦水分生产函数腾发量与产量的试验结果
分别用TSO和ITSO算法求解Jensen模型的敏感指数与SPSS软件中的非线性回归分析方法计算的敏感指数结果进行对比。
本文以Matlab 9.2作为仿真环境,分别采用TSO和ITSO算法对算例进行优化。仿真次数为30,种群数为100,最大迭代次数为500,空间维度为6。经计算后,3种方法计算得到的敏感指数对比如表3所示。

表3 以冬小麦为例的Jensen模型敏感指数
由表3可知,TSO算法和ITSO算法寻优的结果相差不大,但都与SPSS软件中非线性回归分析计算的结果相比有较大差异。将用SPSS软件、TSO和ITSO算法求出的水分敏感指数以及相应阶段的腾发量代入式(1),求得计算的相对产量。在3种条件下,将计算的相对产量与实际相对产量的相对误差进行对比,结果见表4。
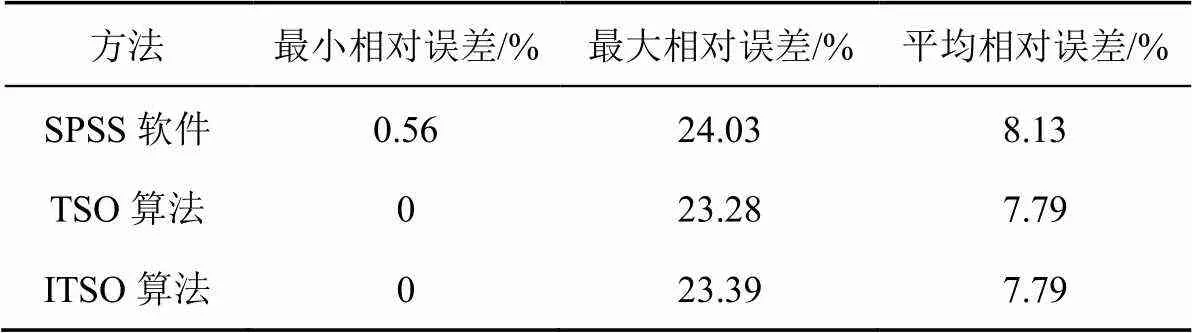
表4 3种方法下计算的相对产量与实际相对产量的误差比较
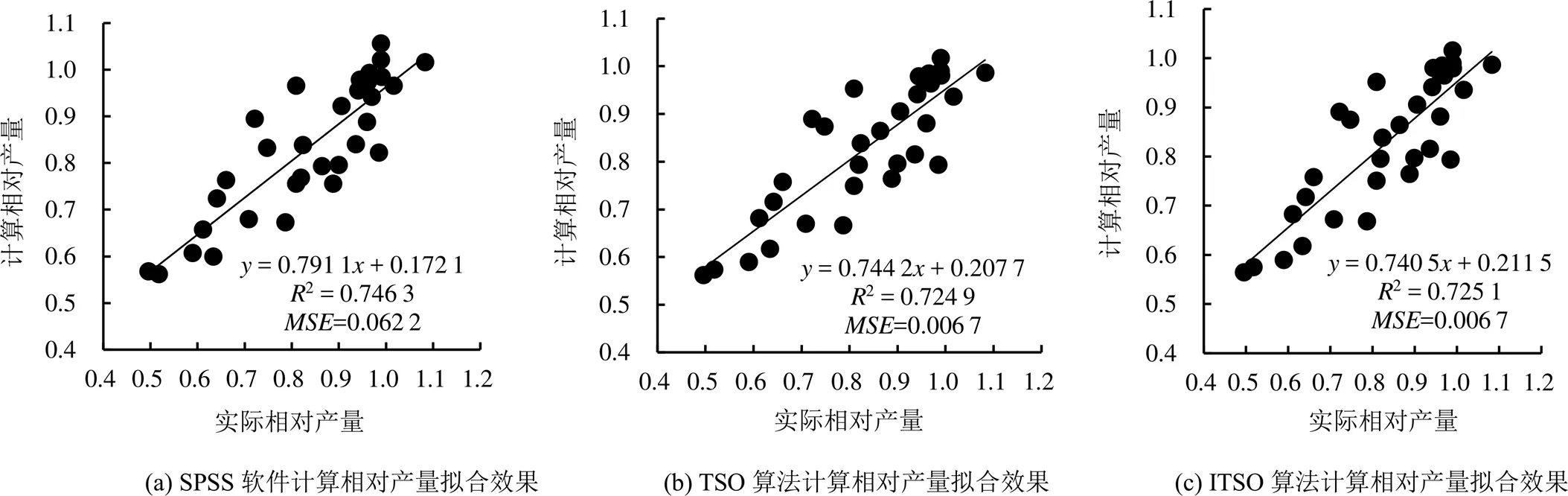
图2 计算相对产量拟合效果
由图2可以看出,用TSO算法和ITSO算法计算得出相对产量与实际相对产量拟合效果同SPSS软件中非线性回归分析得出的拟合效果比较相差不大,但由表4可知,TSO算法和ITSO算法计算得出的相对产量与实际相对产量的误差均小于用SPSS软件中非线性回归分析计算所得结果,并且TSO算法和ITSO算法在求解时候不需要输入简化后的数据,而SPSS软件中非线性回归分析需要将数据进行求取对数运算,对原变量不是无偏的。综上可得,TSO算法和ITSO算法在一定程度上优于用SPSS软件中非线性回归分析方法求解。由表5可知,在相同的MATLAB9.2的仿真环境中,在同一计算机上运行此程序,满足预定精度的条件下,TSO寻优需要6.68 s,而ITSO寻优仅需要6.10 s。由图3可知,TSO算法经过50次迭代后找到最优解,而ITSO算法仅需35次迭代后找到最优解,可见ITSO算法的寻优速度更快。由此说明,ITSO算法在求解Jensen模型作物水分敏感指数要优于TSO算法求解。

表5 应用算例计算结果统计与比较
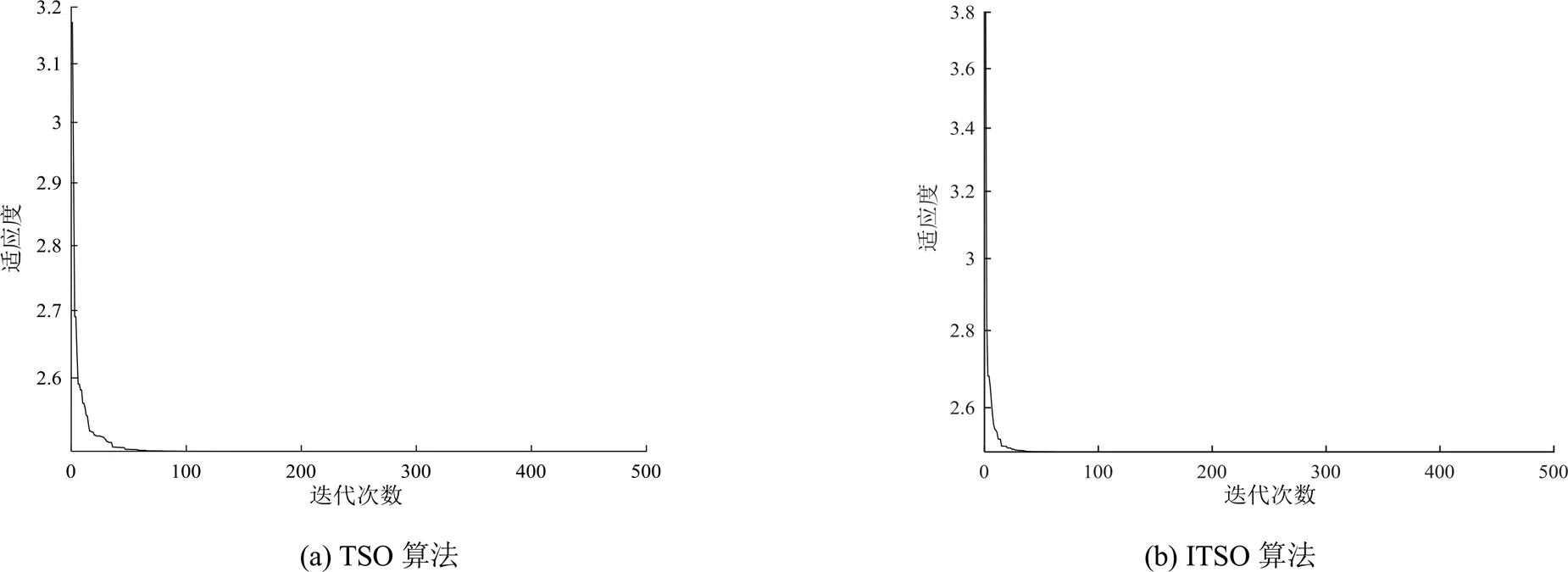
图3 适应度变化曲线
2.3 参数验证
利用ITSO算法求出的水分敏感指数应用到山西省中心灌溉试验站2018—2020年冬小麦预报灌溉试验数据中,数据如表6所示。

表6 山西省中心灌溉试验站冬小麦预报灌溉腾发量与产量试验数据
根据式(1)分别求出3 a计算的相对产量,并分别将3 a计算的相对产量与实际相对产量进行计算,计算结果如表7所示。从表7可以看出,2018、2019年和2020年的2值分别为0.989 0、0.940 9、0.993 8,由ITSO算法求出的水分敏感指数可以在年际间移用,且拟合效果很好。

表7 2018—2020年计算结果
3 讨论
基于分布估计的金枪鱼群优化算法(ITSO)适用于Jensen模型参数求解且算法简单、求解精度高。取文献[4]中某日光温室青椒试验场的试验数据,利用ITSO算法求得Jensen模型参数,其水分敏感指数结果与王喜芹等[4]研究结果基本吻合,二者的敏感指数相差范围在0.010~0.045之间,相对误差范围在3.6%~12.3%之间,但水分敏感指数增减趋势一致,ITSO算法计算得出的相对产量与实际产量的平均误差比用SPSS软件计算得出的结果小0.6%。2种算法类型不同,其中ITSO属于群智能优化算法,SPSS是统计分析软件,而且二者在数据输入上也有差别,ITSO算法不需要输入简化的数据,SPSS需要对数据进行对数运算后输入,所以导致2种方法求得的水分敏感指数数值不同。利用北京永乐店试验数据[22],引入ITSO算法求得敏感指数结果与郑文超等[5]研究结果基本吻合,SMPSO算法和ITSO算法所求得的水分敏感指数数值相同,也间接证明了ITSO算法适用于Jensen模型参数求解。但在同一适应度函数下,郑文超等[5]利用SMPSO算法得出的最好适应度函数值为0.358 2,而ITSO算法得出的最好适应度函数值为0.356 3。这是因为在水分敏感指数求解问题上,ITSO算法寻优性能上要优于SMPSO算法,所以最好适应度函数值小于SMPSO算法得出的最好适应度函数值。取文献[23]中试验数据,用ITSO算法对内蒙古临河市巴盟水科所玉米敏感指数进行求解,这与朱伟峰等[6]研究结果基本吻合,虽然ITSO算法率定的模型参数SSE略大,但比朱伟峰等[6]用自由搜索算法(free search, FS)率定得出的模拟产量与实际产量的平均误差要小0.05%。FS算法和ITSO算法都是群智能优化算法,但FS算法相比较于ITSO算法而言,具有更强的自由性和不确定性,使得二者针对同一问题时产生了不同结果。
作物水分生产函数有很多种表达形式,其模型参数大多依据有限的试验数据进行率定,准确度方面有待进一步提高。可以通过大量已有的试验结果建立数据库并联合智能优化算法,探索模型参数反演研究,使得不同地区、不同作物,有限的数据输入便可得到真实可靠的模型参数。实现模型参数反演,不仅对模型的应用起到了推动作用,更是一种智能化的进步。
4 结论
1)使用CEC2017的29个测试函数测试了ITSO算法的性能,对比ITSO、TSO、GWO、WOA、SSA和BOA算法的寻优性能,由综合均值和标准差可知ITSO算法寻优度高且结果稳定。
2)采用ITSO算法求解Jensen模型参数,拟合精度高。ITSO算法分别于与SPSS软件中非线性回归分析和TSO计算得出的结果进行对比,平均相对误差分别为7.79%、8.13%和7.79%。
3)TSO算法经过50次迭代后找到最优解,而ITSO算法仅需35次迭代后找到最优解。基于分布估计的金枪鱼群优化算法(ITSO)寻优速度最快,能够获得更优的求解结果。
4)采用基于分布估计的金枪鱼群优化算法ITSO,可为Jensen模型参数求解提供一种新的精确途径,为智慧灌溉提供一种智能算法,具有较好的应用前景。
[1] 李中恺, 刘鹄, 赵文智. 作物水分生产函数研究进展[J]. 中国生态农业学报, 2018, 26(12): 1 781-1 794.
LI Zhongkai, LIU Hu, ZHAO Wenzhi. Revisiting crop water production functions in terms of cross-regional applications[J]. Chinese Journal of Eco-Agriculture, 2018, 26(12): 1 781-1 794.
[2] 王仰仁, 雷志栋, 杨诗秀. 冬小麦水分敏感指数累积函数研究[J]. 水利学报, 1997(5): 29-36.
WANG Yangren, LEI Zhidong, YANG Shixiu. Cumulative function of sensitive index for winter wheat[J]. Journal of Hydraulic Engineering, 1997(5): 29-36.
[3] 肖俊夫, 刘战东, 段爱旺, 等. 中国主要农作物分生育期Jensen模型研究[J]. 节水灌溉, 2008(7): 1-3, 8.
XIAO Junfu, LIU Zhandong, DUAN Aiwang, et al. Study on Jensen model at each growing stage for main crops in China[J]. Water Saving Irrigation, 2008(7): 1-3, 8.
[4] 王喜芹, 左建军, 刘婷婷, 等. 基于SPSS软件对作物水分生产函数的计算[J]. 现代农业科技, 2013(11): 230, 233.
WANG Xiqin, ZUO Jianjun, LIU Tingting, et al. Calculation of crop water production based on SPSS software[J]. Modern Agricultural Science and Technology, 2013(11): 230, 233.
[5] 郑文超, 董雯雯. 基于单纯形微粒群优化算法Jensen模型参数求解[J]. 水科学与工程技术, 2013(5): 71-75.
ZHENG Wenchao, DONG Wenwen. Jensen model calculate parameters base on simplex particle swarm optimization algorithm[J]. Water Science and Engineering Technology, 2013(5): 71-75.
[6] 朱伟峰, 王斌, 姜宁. 利用Free Search算法推求作物水分响应Jensen模型参数[J]. 南水北调与水利科技, 2018, 16(6): 142-147.
ZHU Weifeng, WANG Bin, JIANG Ning. Estimation for parameters of Jensen model using free search algorithm[J]. South-to-North Water Transfers and Water Science & Technology, 2018, 16(6): 142-147.
[7] XIE L, HAN T, ZHOU H, et al. Tuna swarm optimization: a novel swarm-based metaheuristic algorithm for global optimization[J]. Computational Intelligence and Neuroscience, 2021, 2021: 9210050-22.
[8] 何春燕, 张忠, 何新林, 等. 作物水分生产函数及灌溉制度优化的研究进展[J]. 水资源与水工程学报, 2007, 18(3): 42-45.
HE Chunyan, ZHANG Zhong, HE Xinlin, et al. Advances in research on the crop water production functions and optimal irrigation schedule[J]. Journal of Water Resources and Water Engineering, 2007, 18(3): 42-45.
[9] 程卫国, 卢文喜, 安永凯. 吉林省水稻水分生产函数模型的适应性研究[J]. 灌溉排水学报, 2015, 34(2): 61-66.
CHENG Weiguo, LU Wenxi, AN Yongkai. Adaptability of water production function models for rice in Jilin province[J]. Journal of Irrigation and Drainage, 2015, 34(2): 61-66.
[10] 韩松俊, 王静, 刘群昌, 等. 三种作物水分生产函数模型的适用性比较[J]. 灌溉排水学报, 2009, 28(4): 10-13.
HAN Songjun, WANG Jing, LIU Qunchang, et al. Evaluation of the applicability of three crop water production functions[J]. Journal of Irrigation and Drainage, 2009, 28(4): 10-13.
[11] HENNESSY J L, PATTERSON D A. Computer architecture: A quantitative approach[J]. Microelectronics Journal, 2007, 28(5): 599-600.
[12] LI Y T, HAN T, ZHAO H, et al. An adaptive whale optimization algorithm using gaussian distribution strategies and its application in heterogeneous UCAVs task allocation[J]. IEEE Access, 2019, 7: 110 138-110 158.
[13] 屈承珺, 纪昌明, 张验科, 等. 基于模拟退火的改进分布估计算法研究[J]. 计算机应用研究, 2020, 37(S1): 138-139, 142.
QU Chengjun, JI Changming, ZHANG Yanke, et al. Research on improved estimation of distribution algorithm based on simulated annealing[J]. Application Research of Computers, 2020, 37(S1): 138-139, 142.
[14] AWAD H N, ALI Z M, LIANG J J, et al. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization[R]. Singapore: Nanyang Technological University, 2016.
[15] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[16] XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science& Control Engineering, 2020, 8(1): 22-34.
[17] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Solfware, 2014, 69: 46-61.
[18] ARORA S, SINGH S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft Computing, 2019, 23(3): 715-734.
[19] 周智伟, 尚松浩, 雷志栋. 冬小麦水肥生产函数的Jensen模型和人工神经网络模型及其应用[J]. 水科学进展, 2003, 14(3): 280-284.
ZHOU Zhiwei, SHANG Songhao, LEI Zhidong. Jensen model and artificial neural network model and its application about water and fertilization Production Parameters of winter wheat[J]. Advance in Water Science, 2003, 14(3): 280-284.
[20] 张硕硕. 冬小麦-夏玉米复种连作灌溉制度优化研究[D]. 郑州: 华北水利水电大学, 2020.
ZHANG Shuoshuo. Optimization of irrigation schedule of winter wheat-summer maize multiple continuous cropping[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2020.
[21] 高丽华. 基于Jensen模型的冬小麦非充分灌溉研究[D]. 天津: 天津农学院, 2014.
GAO Lihua. Study on the deficit irrigation of winter wheat based on Jensen’s model[D]. Tianjing: Tianjin Agricultural University, 2014.
[22] 缴锡云, 雷志栋, 彭世彰. 建立作物水分生产函数的稳健回归方法[J]. 灌溉排水学报, 2006, 25(3): 30-33.
JIAO Xiyun, LEI Zhidong, PENG Shizhang. Robust regression to build crop water production function[J]. Journal of Irrigation and Drainage, 2006, 25(3): 30-33.
[23] 魏占民. 干旱区作物-水分关系与田间灌溉水有效性的SWAP模型模拟研究[D]. 呼和浩特: 内蒙古农业大学, 2003.
WEI Zhanmin. Study on crop-water relationship and availability of field irrigation water based on SWAP model simulation in arid area[D]. Hohhot: Inner Mongolia Agricultural University, 2003.
Calculating the Coefficients in the Jensen Model Using the Tuna Swarm Optimization Algorithm
XUE Ping1, LIU Ling1*, WANG Yangren2, SUN Shuhong2
(1. College of Computer and Information Engineering, Tianjin Agricultural University, Tianjin 300384, China; 2. College of Hydraulic Engineering, Tianjin Agricultural University, Tianjin 300384, China)
【Objective】The Jensen formula is a nonlinear model for calculating the response of crop yield to water and nutrient applications. It contains a number of parameters which need calibration against experimental data. The aim of this paper is to present a method to inversely estimate these parameters using experimental data.【Method】The method is based on the tuna swarm optimization algorithm (TSO). A distribution estimation (ITSO) was used to form the tuna swarm optimization algorithm (TSO), and the performance of the proposed tuna swarm optimization algorithm was verified against other algorithms based on the CEC2017 test. The accuracy and efficiency of the method were compared with other methods based on experimental data obtained from the Xiaohe Irrigation Experimental Station in Shanxi province.【Result】Comparing the performance of ITSO, TSO, GWO, WOA, SSA and BOA methods shows that the proposed algorithm is the best. Comparing ITSO with the nonlinear regression analysis in the SPSS software and TSO shows that the relative error of the proposed method is 7.79%, 8.13% and 7.79%, respectively. The TSO algorithm converged in 50 iterations, while the ITSO algorithm found the optimal solution in just 35 iterations. 【Conclusion】The tuna swarm optimization algorithm combined with the distribution estimation (ITSO) is efficient for estimating the parameters in the Jensen model. It is highly accurate and converges fast.
crop water production function; Jensen model; model parameter solution; distribution estimation; Tuna swarm optimization algorithm
薛萍, 刘玲, 王仰仁, 等. 基于金枪鱼群优化算法的Jensen模型参数求解[J]. 灌溉排水学报, 2022, 41(11): 22-29.
XUE Ping, LIU Ling, WANG Yangren, et al. Calculating the Coefficients in the Jensen Model Using the Tuna Swarm Optimization Algorithm[J].Journal of Irrigation and Drainage, 2022, 41(11): 22-29.
1672 - 3317(2022)11 - 0022 - 08
S274
A
10.13522/j.cnki.ggps.2022022
2022-01-12
现代都市农业智慧灌溉技术项目(XB202016)
薛萍(1997-),女。硕士研究生,主要从事智慧灌溉研究。E-mail: 1135322342@qq.com
刘玲(1976-),女。副教授,硕士,主要从事计算机仿真与优化研究。E-mail: 107916787@qq.com
责任编辑:白芳芳

