基于元路径的异构信息网络的影响力建模

朱继阳

(国家电网内蒙古东部电力有限公司信息通信分公司，内蒙古，呼和浩特 010010)

0 引言

随着在线社交网络的出现和快速发展，极大地促进了信息、经验和思想在社会网络中的传播，使越来越多的人在他人的影响下改变自己的决策和行为[1-2]。定性和定量地衡量个人对他人的影响，有助于识别有影响的个人，了解人们的社会行为，促进政治、经济和文化活动的传播，为社会平台的设计和应用提供重要的见解。社会影响力的强弱取决于个体之间的关系、网络距离、时间、网络和个体的特征等。为了衡量社会影响力，提出了话题不经意、基于话题和基于对的影响力评价模型。大多数影响评估模型都集中在包含相同类型节点或边的同质信息网络上。然而，在现实世界中，网络通常包含多种类型的节点或边，称为异构信息网络(HIN)[3-5]。由于HIN比同类信息网络能够建立更为复杂的关系、结构和丰富的语义信息，因此对异类信息网络的影响评价可能比同类信息网络的影响评价更为全面和有效。然而，节点和边缘的异质性给影响评估带来了新的挑战，传统的同质网络影响评估模型不能直接应用于HIN[6-9]。因此，本文提出了一个基于元路径的信息熵模型来模拟异质信息网络中的社会影响。该模型首先通过相应的元路径从HIN中提取出多个同质网络，然后度量这些同质网络中的直接影响和间接影响，通过整合链接熵来评估朋友数量对社会影响的影响，而互动频率熵则从互动次数来评价对社会影响力的影响。最后，将同质网络学习到的直接影响和间接影响融合在一起。

1 提出的方法

本文提出了一个基于元路径的信息熵模型来模拟HIN中的社会影响，称为MPIE。它由三个部分组成，将一个原始的HIN转换成几个同质网络;用信息熵来描述社会影响的复杂性和不确定性;融合元路径下节点的影响[10-11]。

1.1 基于元路径的同构网络

社会影响是两个实体为某一特定行为而建立的关系。特别地，一个实体通过执行动作来影响其他实体。在HIN中，有多条对称的元路径连接同一类型的节点，如DBLP中的“作者—论文—作者”和“作者—论文—会议论文—作者”。基于这些路径，作者具有不同的影响力。这里利用一组元路径P={P0,P1,…,Pl,…,P|p|}来提取语义信息，并将HIN G转换成若干个同构网络GP={Gp0,Gp1,…,Gpl,…,Gp|P|}。每个同构网络Gpl包含一种语义信息，即每个节点都通过元路径Pll与其邻居相连。

定义1 交互矩阵。给定一个基于元路径Pl=(k1k2…kl)的齐次网络Pi，齐次网络Gpi的交互矩阵Mpi描述如下：

MPl=Wk1k2Wk2k3…Wkl-1kl

(1)

其中，Wkikj是ki类型和kj类型之间的邻接矩阵，如果对象i∈ki连接到对象j∈kj，则Wkikj(i,j)=1。例如，在DBLP中，如果作者a1∈A发表了一篇论文p1∈P，WAp(a1,p1)，其中A是作者集，P是论文集。

在同构网络GPl中，如果对象ki和对象kj通过元路径Pl连接m次，则MPi(ki,kj)=m，其中，m表示元路径p下对象ki∈Ki和对象kj∈Kj之间的路径实例Pl的个数。

1.2 基于信息熵的社会影响测度

对于同质信息网络中节点的影响，可以发现其背后的直觉是，一个对象的影响不仅应该是直接的强关联，而且应该是间接的强关联。正式给出了社会影响的定义。

全球影响力与直接/间接影响力有着密切的关系。例如，如果一个用户对其他用户有很强的影响力，那么他很可能在全球范围内有影响力。在这项工作中，只考虑同一类型节点之间的影响，例如用户之间的影响。不同类型节点之间的影响，如作者对论文的影响或论文对作者的影响，由于难以进行有意义的解释和定量的度量，的工作中没有包括这些节点之间的影响。

(1) 直接影响计算

在社会网络中，如果两个节点通过边连接，则节点u对节点v有影响，称为链接熵。如果节点u和节点v多次交互，则节点u对节点v的影响较大，称为交互熵，例如在DBLP网络中，作者A和作者B之间的合作越多，A对B的影响就越大，因此，节点的直接影响由两部分组成：链路熵和交互熵。

(2)

(3)

(4)

(2) 间接影响计算

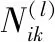
图1 只有一个公共节点

图2 三个公共节点

(5)

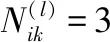
(6)

根据以上分析，均匀网络GPl中的间接影响描述如下：

(7)

(3) 计算节点总影响

(8)

1.3 融合影响

在不同的元路径下，节点的影响是不同的。为了计算更全面的影响，给每个元路径分配1个统一的权重，这意味着影响在路径上的扩散偏好。该权重向量表示为ω∈R1×|P|，并且ωl表示元路径Pl上的权重。HIN中节点i的最终影响表示为Ii，可以是每个元路径下影响的加权和。

(9)

2 实验

通过2个应用程序来评估MPIE：影响的传播范围和影响的排名。

2.1 数据集

采用了2种广泛使用的不同领域的数据集，包括来自学术领域的DBLP数据集[12]和来自商业领域的Yelp数据集[13]。包括20个地点和前5 000名作者，其中13 245个术语来自4个领域：数据库、数据挖掘、机器学习和信息检索。Yelp数据集记录了用户对本地业务的评分，包括16 239个用户和14 282个本地业务，其中198 397个评分从1到5。

2.2 baseline方法

为了证明所提出的MPIE的有效性，将MPIE与齐次方法和MPIE的一个变种进行了比较。一般来说，大多数影响测量方法只能用于同质网络。为了使这些方法在同构网络中适用于HIN，在实验中忽略了对象和关系之间的语义差异，将它们视为同一类型。考虑采用以下方法进行比较：度中心度(DC)、PageRank、基于熵、MPIE direct、MPIE。

在这些方法中，基于HIN的方法需要使用不同的元路径。根据小世界现象，可以推断，当元路径长度大于5时，这种关系非常弱。而且长的元路径可能会引入噪声语义[13]，所以只选择最多4步的短元路径。同时，由于节点间的边限制，选择了节点间关系密切的元路径。在表1中给出了使用的元路径。另外，为了得到每种算法的影响扩散，选取top-k个影响节点作为种子，其中k分别选取5,10,20,30,40,50。

表1 两个数据集选择元路径

2.3 实验结果

(1) 影响范围

在社交网络中，有影响力的用户可以在短时间内将信息传播给大量用户。为了评估影响的扩散范围，借用线性阈值(LT)来模拟影响在HIN中的扩散，在相同的种子数下，激活节点数越多，影响度量就越有效。图3显示了具有不同k个影响节点的不同算法的影响扩散范围，其中MPIE融合了表1中的3条元路径，统一权重为0.33。可以观察到，由于数据分布的不同，不同的算法在不同的数据集上表现出不同的性能，并且随着k值的增加，影响扩散的数量也随之增加。这归因于这样一个事实，即节点种子集越大，受影响的节点就越多。

首先，在这些基线中，所提出的MPIE方法比基线(DC、PageRank和Entropy-base)具有更好的性能，这表明异质信息可以改善扩散范围。总体而言，基于DC、PageRank和熵的算法的性能并不稳定，更多地依赖于数据集中特定数据的特征和分布。例如，Yelp中的节点分布比4区域更均匀，因此在Yelp中DC的性能更好。当使用元路径来表示HIN时，忽略节点和链接类型的基于熵的方法的性能比MPIE差，MPIE可能包含有用的证据来验证在HIN中考虑节点类型的重要性。

(a) 4-area

接下来，考虑到MPIE变体MPIE direct，很容易看出MPIE direct的性能比MPIE差。主要区别在于影响成分。MPIE direct只考虑直接影响，忽略了间接影响。因此，在HIN中考虑间接影响是有意义的，这使得影响测量更有效，传播更广泛。

(2) 节点的秩

在大多数情况下，人们更多地关注一些有影响力的节点，通过融合表1中的3条元路径，基于MPIE评估节点的重要性。

表2显示了这5种方法估计的总影响排名前十位的作者，忽略了对象的异质性，直接在整个4区域网络上运行基线方法，因为它们的结果混合了所有类型的对象，所以从排名列表中选择作者类型作为最终结果。根据5种方法返回的结果，可以得到四区数据集中的5个候选作者排名表。这些方法对作者的排名结果都是合理的，如MPIE排名前三位的作者是Philip S.Yu、Christos Falutos和JiaWei Han，他们都是计算机科学领域非常有影响力的研究者。为了定量地评价排名结果，使用了作者从aminer1的排名作为基本事实。然后使用Kendall’s tau(值介于-1和1之间，越高越好)来比较候选排名列表和标准排名列表之间的差异。表3显示了作者排名表的差异。可以看到，基于熵的方法是最糟糕的，因为简单地将不同类型的节点视为相同类型的节点会丢失潜在的链接信息(例如，2个作者通过论文或地点连接的次数)。MPIE在人类直觉方面给出了最好的排名。

表2 四区域数据集上不同方法

表3 Kendall’s tau测量的四区域数据集上5种测量方法

3 总结

本文研究了异构信息网络中的影响度量问题，旨在研究如何利用丰富的语义信息来度量节点的影响。提出了一种基于元路径的信息熵模型MPIE，通过元路径获取HIN中丰富的语义信息，并用信息熵来度量。然后，简单地融合相应的元路径。此外，在不同类型的异构网络上做了大量的实验，展示了一些有趣的案例，并证明了的方法和节点等级的影响扩散优于基线。但是在本文中，只是通过统一的权值来融合元路径，因此在将来，准备自动学习不同元路径的权值，这有助于在实际系统中提供准确的影响度量，并发现对象之间有趣的关系。