Mo2C二维材料晶格热导率的第一性原理研究

丁迎春， 袁 欢， 徐 明

(1. 西南民族大学 电子信息学院 信息材料四川省高校重点实验室, 成都 610041; 2. 成都信息工程大学 光电工程学院,成都 610225)

1 引 言

近年来，越来越多的新材料不断涌现，其中新型导热材料和新型隔热材料的研究引人注目. 新型二维材料在电子、电催化、储能和热电等方面有广泛的应用[1]. 2011年研究者提出的二维过渡金属碳化物(MXene)是一类新型二维材料，其丰富的化学元素组成及可调谐的表面官能团为其性质的多样化提供了广阔的空间[2]. MXenes 是由过渡金属原子层与金属碳化物或者氮化物原子层交替排列构成的多原子层的新型二维纳米材料[3-7]. 目前，人们已成功合成近10 种M2C型二维材料，如、Ti2C[8]、V2C[9]、Nb2C[9]、Mo2C[10]等.

2020年，Chang 等人通过Na2CO3的碳热还原反应制备了二维Mo2C材料[11]. 其所制备的样品具有规则的层状结构，厚度达到10-15 nm[11]. 在一些表面官能团Tx 修饰下，Mo2CTx和 Mo2TiCTx等材料呈现类似半导体的性质，理论工作表明其具有间接带隙[12]. Zha等人采用了Klemens theory方法，研究了Mo2C本征晶格热导率[13]. 计算发现，在室温下，锯齿方向(zigzag)和扶手椅(armchair)方向的热导率大约为9.72 和16.2 W m-1K-1. 其结构表明2D-Mo2C材料的热导率具有锯齿方向和扶手椅方向各向异性的特征，并且扶手椅方向的热导率要大于锯齿方向[13]. 由于经典的模型研究材料的热输运存在一定局限性，近年来采用玻尔兹曼输运方程来研究2D材料的热输运和电输运已成为一个热点[14-17]. 通过二阶力常数和三阶力常数的计算，可以获取声子传输方程的信息，从而更严格的求解材料的晶格热导率[14-17].

利用第一性原理，结合玻尔兹曼输运方程已被用于研究二维材料Mxene的热导率[18]. 固体热传导的产生的机理主要有两种：①自由载流子(电子和空穴) 的扩散; ②声子( 晶格振动能量子) 的扩散. 晶格热导率主要由声子贡献. 本文基于声子玻尔兹曼输运方程的计算方法，采用DFPT方法考虑简谐近似计算二阶力常数，进一步考虑非简谐近似计算三阶力常数，最后采用玻尔兹曼输运方程计算了二维Mo2C材料的晶格热导率.

2 计算方法

基于密度泛函理论的第一性原理方法[19], 采用VASP软件[20]进行结构优化和单点能的计算，交换关联泛函选取广义梯度近似(GGA) 下的PBE[21]. 优化晶体结构的截断能采用函数截断能取为500 eV. 为了克服层与层之间的相互作用，真空层厚度选择为20 Å. 结构优化至原子受力小于10-5eV·nm-1，能量差收敛到1 × 10-6eV，K点网格选取5 × 5 × 1. 声子谱的计算采用由Phonopy 软件[22]，热导率的计算采用ShengBTE 软件[23]，二阶力常数和三阶力常数都采用有限位移方法. 简谐近似下的原子间二阶力常数的计算采用5×5×1的超原胞和K 点网格选取5×5×1. 非简谐近似下的三阶力常数采用5×5×1 的超原胞5近邻的原子作用. 还进一步测试了8, 10近邻原子作用并计算了三阶力常数. 热导率计算中，考虑K点网格选取30×30×1, 40×40×1 和50×50×1. 测试网格改变引起的晶格热导率小于1%则完成测试，最后选取40×40×1的网格线作为晶格热导率的计算.

晶格热导率由下式得到

(1)

其中CV(qs)是模式热容，vg(qs)为声子群速度τqs是声子的寿命.

3 计算结果与分析

3.1 晶体结构

2D-Mo2C的结构如图1所示，从左边的俯视图可以看到2D-Mo2C属于六角结构 (a)，空间群为P-3M1，群号为164. 图1(c)表示的2D-Mo2C的正交结构的3×3×1超胞. 其中黑框表示2D-Mo2C的正交结构的原胞. 图1(c，d ), 水平方向代表的是锯齿方向方向，垂直方向是扶手椅方向. 本文计算的2D-Mo2C晶格常数为3.001 Å，与他人计算的结果(3.00 Å)符合很好[12, 13].

图1 2D-Mo2C 结构原胞模型(a,b)的正交结构的3×3×1超胞模型(c,d). 2D-Mo2C 结构俯视图(a, c)和侧视图(b, d). 图中大原子代表Mo原子，小原子代表C原子.

3.2 晶格振动和简谐近似

为了研究二维Mo2C 的动力学稳定性和热导率，利用第一性原理方法先计算了二阶力常数，并得到其声子谱(a)和声子态密度(b)(如图2 所示). 声子谱是表示组成材料原子的集体振动模式. 如果材料的原胞包含n个原子，那么声子谱总共有3n支，其中有3条声学支，3n-3条光学支. 声学支表示原胞的整体振动，光学支表示原胞内原子间的相对振动. 由于二维Mo2C结构的原胞有2个Mo 原子和1个C原子，因此声子谱(a)由三支代表质心运动的声学支以及6个代表原胞内各原子相对于质心运动的光学支组成. 声子谱在图2(a)中没有发现声子的负振动模，表明该结构的声子谱没有虚频，说明二维Mo2C是一种动力学上能够稳定存在的二维材料. 我们的结果和查等人[13]计算得出的声子谱是一致的. 从图2(a)可知，Mo2C的声子散射图中有3 支声学振动模式及6 支光学振动模式，从下到上依次为面外声学横波(ZA, 黑色) 、面内声学横波(TA，红色) 、面内声学纵波(LA，蓝色) . ZA、TA 和LA 的3 支声学声子在Γ 点附近均呈近似线性变化，而石墨烯ZA 支声学声子在Γ 点成二次函数变化[20]. Mo2C的最高振动频率(21.35 THz) 出现在倒空间的M点，通过θ = hν /k 估算得到材料的德拜温度约为160.32 K，该数值与刘刚等人研究的α-selenene 材料的德拜温度(163 K)的值接近[14]. 从图2计算得到的声子谱中可以看到，频率 12.5 THz以下的光学支有三支，20 THz附近光学支也有三支. 这些光学支之间形成了很大的光学声能隙(大约12 THz)，说明Mo 原子和C原子具有很强的离子性. 这是由于2D-Mo2C材料中的两种元素原子量相差很大所致. 根据声子理论可以知道，对于晶体中的原子，其振动频率通常与质量成反比，所以高频部分通常由质量较小的原子贡献，而低频部分由质量较大的原子贡献. 从计算的元素贡献的声子分态密度图2(b)可知，由于Mo的原子量为(95.9)，是C原子量(12)的8倍，所以，Mo元素在声子谱态密度的低频(7.5 THz以下)区域占主导部分，此频率范围都由Mo元素的振动贡献. 而在对应的高频部分(20 THz附近)，主要由材料中的C原子贡献. 本文计算的结果完全符合声子振动的规律.

图2 2D-Mo2C的晶格振动声子谱 (a)和元素贡献的声子态密度(b)

3.3 晶格热导率

经过测试，采用网格为40 × 40× 1计算晶格热导率. 计算的热导率如图3所示. 计算结果表明2D-Mo2C在锯齿方向 (zigzag)和扶手椅方向 (armchair)的热导率与温度之间成反比例关系. 计算还发现2D-Mo2C沿锯齿方向和扶手椅方向的晶格热导显示出很强的各向异性. 计算得到的热导率数值和查等人[13]采用Klemens theory理论计算的结果基本一致. 但是查等人[13]采用Klemens theory理论得到的热导率，锯齿方向的热导率小于扶手椅方向的热导率，与本文采用玻尔兹曼输运方程得到的结果正好相反. 本文采用玻尔兹曼输运方程得到的结果在两个方向上的热导率都是小于查等人[13]采用Klemens theory理论得到的两个方向上的热导率. 本文计算得到的结果显示，在300 K时，在锯齿方向(zigzag)和扶手椅 (armchair)方向的晶格热导率分别为7.20 和5.04 W m-1K-1，查等人得到的是9.72 和16.2 W m-1K-1[13]. 这些计算都表明，2D-Mo2C材料具有较小的晶格热导率，轻微大于α-selenene 材料的热导率(3.04 W m-1K-1)[14]. 在900 K以上，两个方向的热导率各向异性减小，差异约为2.0 W m-1K-1左右.

图3 2D-Mo2C 的晶格热导率

进一步研究了2D-Mo2C 的各种晶格振动模式下的晶格热导率，如图4所示. 计算发现，锯齿方向(zigzag)和扶手椅 (armchair)方向的声子分支对晶格热导率的贡献基本一致. 200 K以下，TA是占绝对主导，其次是LA，贡献最少的是光学支(O). 在300 K-500 K区间(如图4(a, b))，声学支 TA和 LA，ZA贡献的热导率明显降低，光学支O贡献会轻微升高. 在500 K附近，光学支O贡献对热导率的贡献和TA声学支贡献基本一样. 温度超过500 K后，ZA对总热导率的贡献就非常小了. 在更高温度，光学支O模式超过LA模式的贡献，成为热导率的次要贡献. 计算得到该材料由于起伏型结构导致ZA 支对热导率的贡献减小，与王文华等人研究相同起伏结构的β 型结构锑烯材料的声学支ZA对热导率有最小贡献是一致的[15].

图4 2D-Mo2C 的模式晶格热导率

3.4 声子群速度和弛豫时间

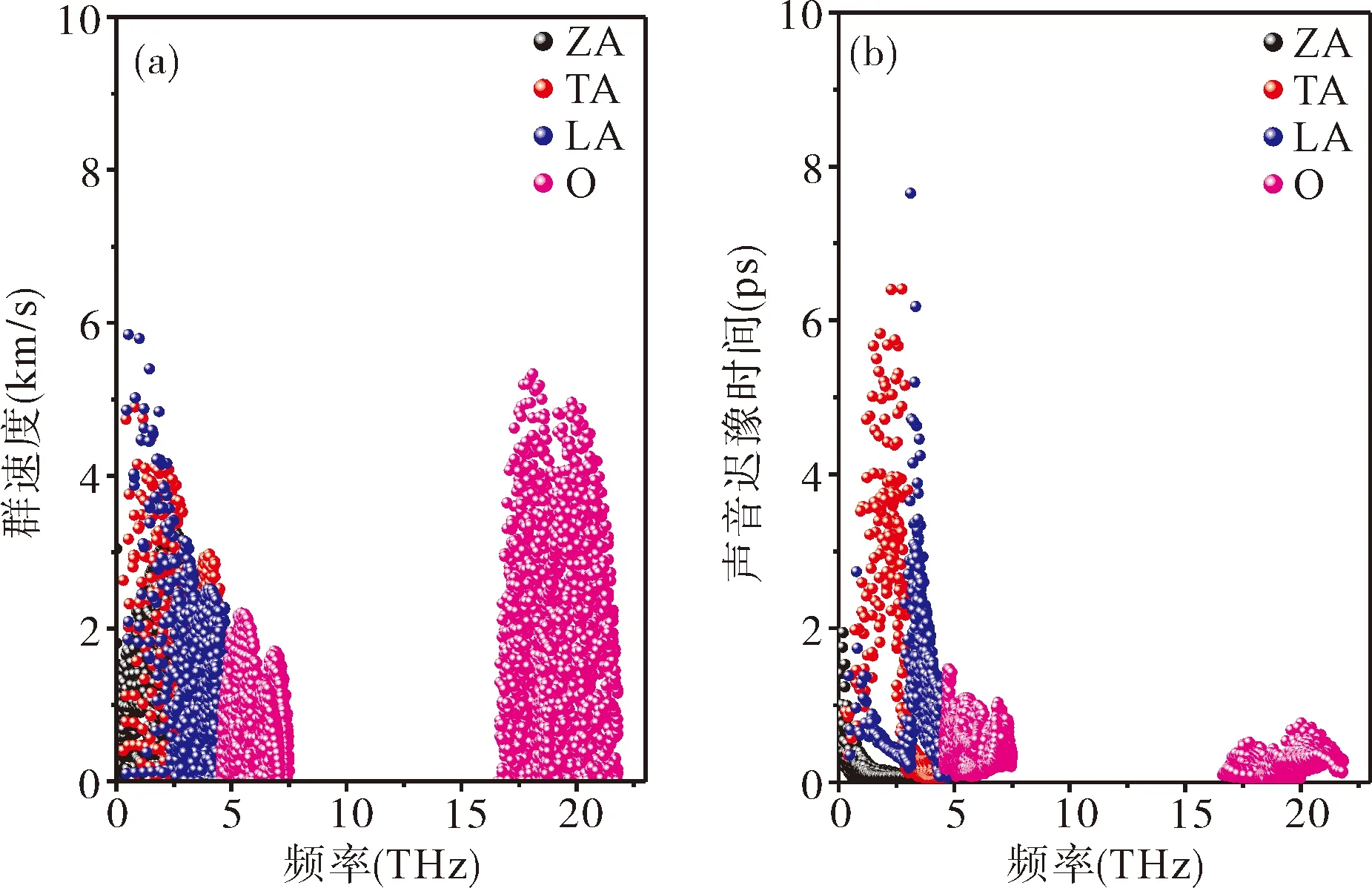
图5 300 K下2D-Mo2C材料的所有模式的声子群速(a) 和声子弛豫时间(b)

从图5(b)可知，ZA声学支对应的弛豫时间都在2 ps以下，TA, LA模式下的声子弛豫时间较大，少数TA, LA模式具有大的弛豫时间(超过6 ps). 在4-7.5 THz范围，声子的光学支O贡献的群速度较高，且只有少数光学支声子群速度能达到6 km/s左右. 因此，声学支具有大的弛豫时间，光学支具有相对小的弛豫时间. 三支声学振动模式具有较大弛豫时间，对晶格热导率贡献较大.

刘刚等人研究的几种2D selenene材料都具有较小的弛豫时间[14]. 这些材料和Mo2C材料都具有很小的热导率. 彭博等人[24]研究的stanene材料和Mo2C材料相比，则具有相对低的群速度，但是stanene材料具有非常大的弛豫时间(1000 ps 的数量级). 可以推断和计算出2D-Mo2C的热导率比stanene材料的晶格热导率要低. 贺等人研究发现2D-C4N3H材料具有大的群速度和大的弛豫时间，所以C4N3H具有较大的热导率[25].

从图5(b)可以发现，2D-Mo2C光学支振动模式下的弛豫时间对材料晶格的热导率的影响也非常小. 所以，对2D-Mo2C材料热导率的贡献，主要是不同模式声子的群速度和三个声学支振动的弛豫时间的作用所致.

3.5 散射空间和模式格律乃森参数

三声子散射进程直接用于估计可以用于三声子散射过程中每种声子的模式数量. 相空间的三声子模式散射代表了一定数量的声子散射的通道，严格遵从能量和准动量条件的收敛[26, 27]. 模式模式格林艾森参数代表声子模式的非简谐振动，它决定每一个声子散非谐效应的强度[27]. 通常情况下，更有效的散射，对应更大的声子散射率和大的模式格林艾森参数，材料就有相对较小的本征晶格热导率[23-28]. 300 K时，所有声子振动模式下的三声子散射过程如图6 (a)所示，其模式格林艾森参数如图6 (b)所示. 三声子散射过程和声子模式格林艾森参数是相空间散射中声子-声子散射的两个关键因素. 如图6(a)所示，2D-Mo2C材料在一定频率范围内具有大的总的散射空间，特别是ZA模式对应的散射空间，TA, LA依次变小，所有的光学O振动模式是最小的. 声子支振动模式(TA, LA)的散射空间更大，而光学振动模式贡献的散射非常小. 图6(b)是计算的不同振动模式格林艾森参数，ZA具有更大的模式，其次是TA, LA, 光学O振动模式的贡献导致较小的模式格林艾森参数. 模式格林艾森参数的范围大约在-75到10，所以， 2D-Mo2C声子振动模式中的TA, LA声学支振动模式具有强烈的非简谐效应，导致2D-Mo2C材料具有较低的晶格热导率.

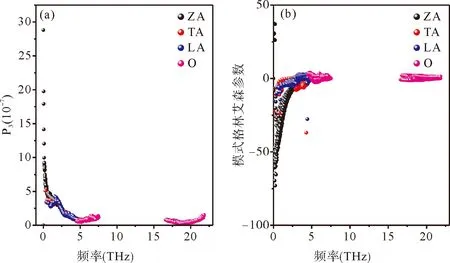
图6 300 K下2D-Mo2C的所有模式的三声子散射过程(a) 和模式格林艾森参数(b)

4 结 论

基于第一性原理方法，结合声子玻尔兹曼输运方程，研究了二维Mo2C材料的晶格热导率. 计算得到的两个方向(锯齿和扶手椅方向)的晶格热导率呈各向异性特征. 室温下，锯齿和扶手椅方向晶格热导率分别为7.20 和 5.04 Wm-1K-1. 计算研究了声学振动和光学振动模式对晶格热导率的贡献情况，揭示总晶格热导率主要由面内声学(TA)横波的振动模式所贡献. 还进一步研究了声子群速度、声子弛豫时间、三声子散射空间和模式格林艾森参数. 在二维Mo2C结构中，声子群速度、声子弛豫时间对晶格传输有重要影响. 二维Mo2C具有较大的声子散射空间和模式格林艾森参数，所以该材料具有较低的导热系数.