加权迭代六边形网络的谱分析
李 美,吴 波
(南京财经大学 应用数学学院,南京 210023)
0 引言
复杂网络作为一门新兴交叉学科,其研究涉及自然界和社会生活的很多方面,例如物理、化学、生物、社会、经济、工程等领域.在复杂网络的研究中,一个核心问题是掌握网络结构,进一步了解网络拓扑结构对网络功能与动态性质的影响.例如,操芳等[1]通过研究网络受到攻击后的平均捕获时间,对比网络受到攻击前后的扩散效率等.近年来,通过大量学者的研究表明网络的拉普拉斯谱也具有重要作用.例如,Klein等[2]根据电网络理论定义了新的函数——电阻距离,称网络中所有节点对之间的电阻距离之和为Kirchhoff指标,它是一个重要的拓扑指标,可以用来分析网络中通讯的可靠性和网络整体的鲁棒性;文献[3]将Kirchhoff指标和拉普拉斯谱联系起来;文献[4]进一步引出了乘法度-Kirchhoff指标,并将其和标准拉普拉斯谱联系起来;此外,Banerjee等[5-6]总结了不同网络的标准拉普拉斯谱的图像,对经典网络进行初步分类.
近年来,许多学者致力于研究网络的谱,包括迭代三角形网络和其他分形网络[7-10].一般情形下,考虑一个具有相应结构的网络只注意节点之间是否存在连边,忽略了节点之间连接的紧密程度,即边的权值.因此,将一般网络推广到加权网络更具有实际意义.但目前,谱的研究尚有诸多困难,除一些特殊结构的网络模型外,谱难以解析研究.本文构造了一类加权迭代六边形网络,在网络的拓扑结构的基础上建立相邻两代网络的特征值和特征向量之间的迭代关系,从而得到网络的标准拉普拉斯谱.
1 加权迭代六边形网络的构成
首先我们介绍加权迭代六边形网络的构造,以r(0<r<1)为参数进行以下的迭代,得到一个加权迭代六边形网络,r称为权重因子.
(i)设G为任意一个简单连通图,每条边的权重为ω=1,称G为初代图;
(ii)用长度为1和5的两条平行路径代替G的每一条边,长度为5的路径即为新生成的路径,5条新边的权重为rω=r.此时,得到一个第一代的加权迭代六边形网络,记作W(G);
(iii)加权迭代六边形网络,用Wn(G)(n≥1)表示,它是由Wn-1(G)迭代产生的.若Wn-1(G)的每一条边ij的权重为ω,则产生4个新节点i′、j′、k′、l′和5条新边ii′、i′j′、j′k′、k′l′、l′j,新边的权重为rω.
图1初始图为三角形的加权迭代六边形网络,展示了该网络前三代的迭代过程,考虑到初始图可以是任意连通图,所以,图1是一个特例.将第n代加权六边形网络Wn(G)的总节点数记作|Nn.|设Wn是网络Wn(G)的广义邻接矩阵,也称为权重矩阵,它是一个阶矩阵,每项元素wn(i,j)定义如下,如果节点i和j有连边,则wn(i,j)是边的权重ωn(i,j),否则是0.设Sn为对角强度矩阵,定义为Sn=其中sn(i)表示节点i的强度,它是节点i的所有邻边的权重之和.于是,拉普拉斯矩阵-L n表示为-L n=Sn-Wn,而转移概率矩阵Tn表示为Tn=Sn-1Wn.
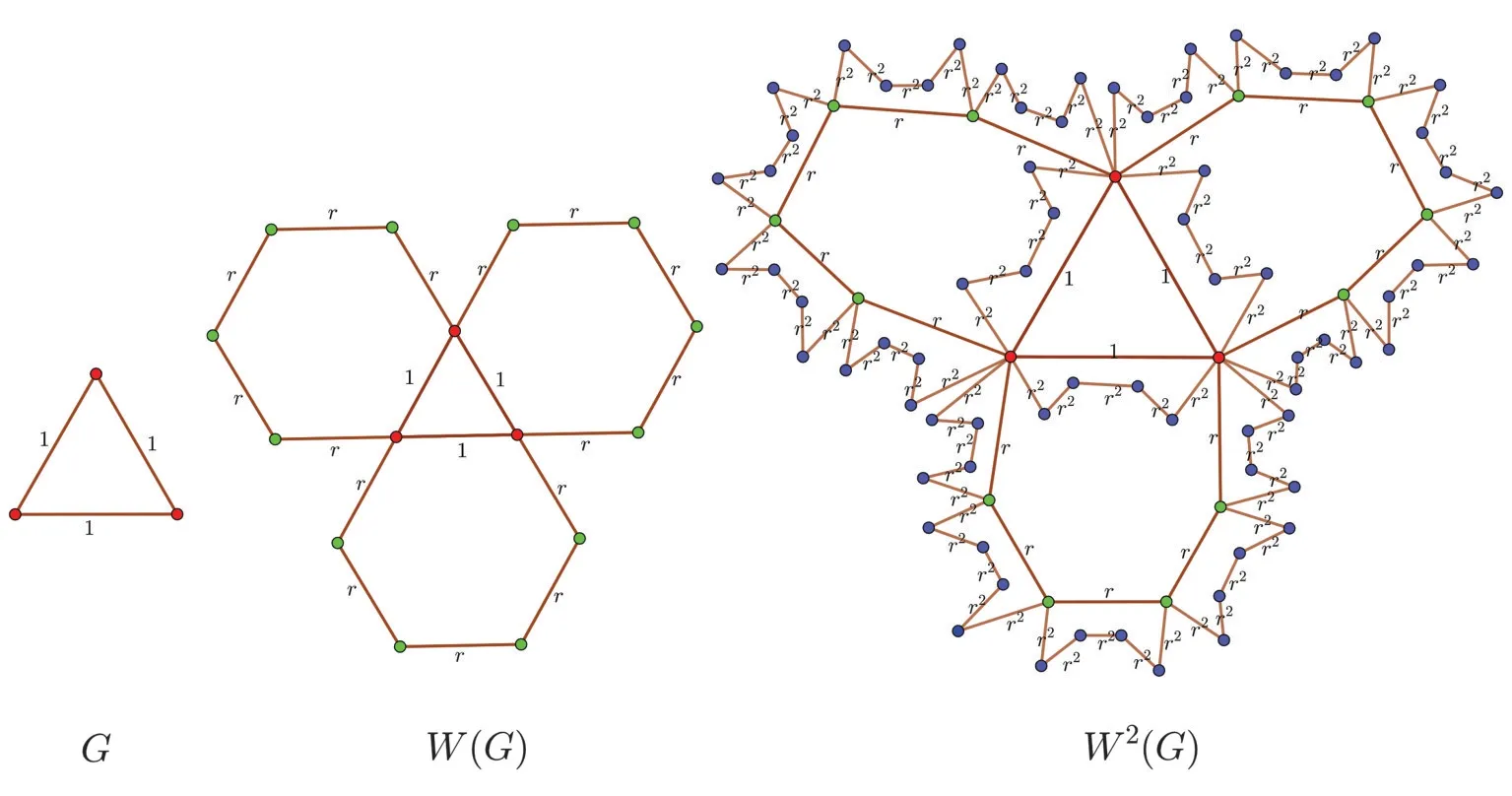
图1 加权迭代六边形网络的前三代
一般情况下,转移概率矩阵Tn是不对称的,但是可以通过标准化将其转化为对称矩阵,称为标准邻接矩阵,记作Pn,定义为
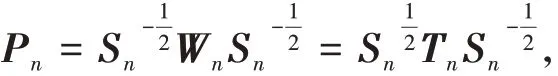
2 加权迭代六边形网络的谱分析
从第n(n≥1)代加权迭代六边形网络Wn(G)开始,根据网络的自相似结构,得到前一代网络Wn-1(G)的标准邻接矩阵的特征值,利用网络的标准邻接矩阵和标准拉普拉斯矩阵之间的联系,得到前一代网络的标准拉普拉斯矩阵的特征值,即得到如下定理.
定理2.1 设λ为网络的标准拉普拉斯矩阵Ln(n>1)的任意一个特征值,λ≠1,r(0<r<1)为权重因子,满足
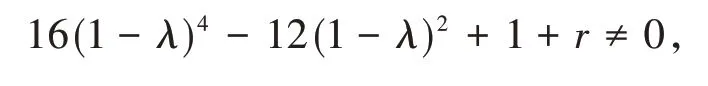
则
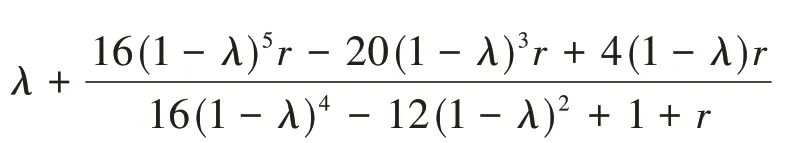
是Ln-1的一个特征值,且它的重数与λ的重数相等.
证明 令Vn是第n代网络Wn(G)的所有节点集,Vn=Voldn∪Vnewn,Vnewn是第n次迭代新加入的节点集,Voldn是所有老节点集(即前一代网络Wn-1(G)的所有节点集).
设Vrk(k=0,1,…,n-1)是父边权重为rk的节点集,
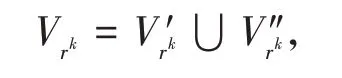
其中:Vr′k=Vrk∩Vnold;Vr″k=Vrk∩Vnnew.
易知,V0∈Vold,Vrn-1∈Vnew.于是
Vn=V0∪V1∪Vr∪…∪Vrn-1=( V0∪V1′∪Vr′∪…∪Vr′n-2)∪( V1″∪Vr″∪…∪Vr″n-2∪Vrn-1).
设v=(v1,v2,…,v|Nn|)是Ln属于λ的特征向量,其中|Nn|为网络Wn(G)的总节点数.
因为Ln=In-Pn,所以1-λ是标准邻接矩阵Pn的特征值,且

于是,对任意的节点i∈Vn,有

同时,根据网络的自相似结构,节点i的强度为
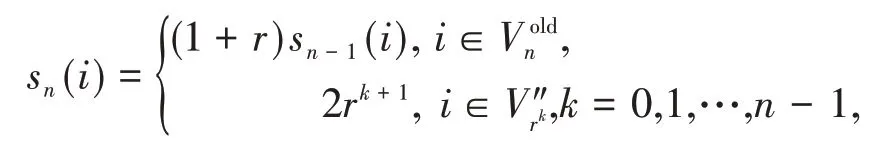
其中V″rn-1=Vrn-1.
为了得到前一代网络的特征值,先考虑每一个老节点i∈V′rm,m=-1,0,1,…,n-2,其中当m=-1时,V′r-1=V0.相应地,有j′r-1=j0,vj′r-1=vj0.
基于网络的自相似结构,节点i和j之间的权重为
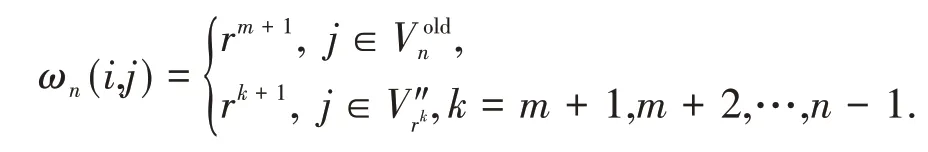
根据式(2)可得
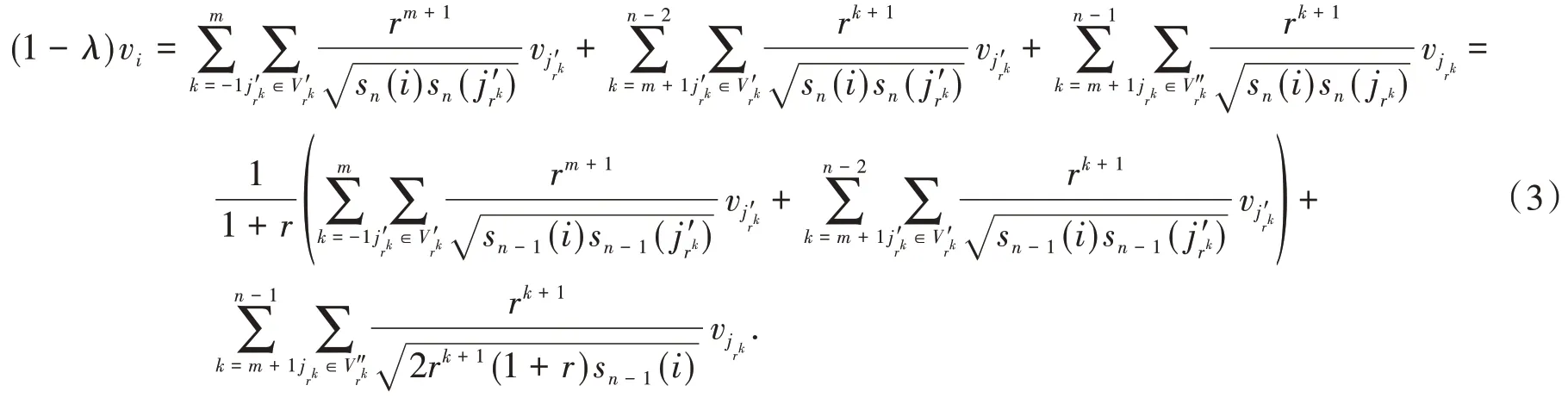
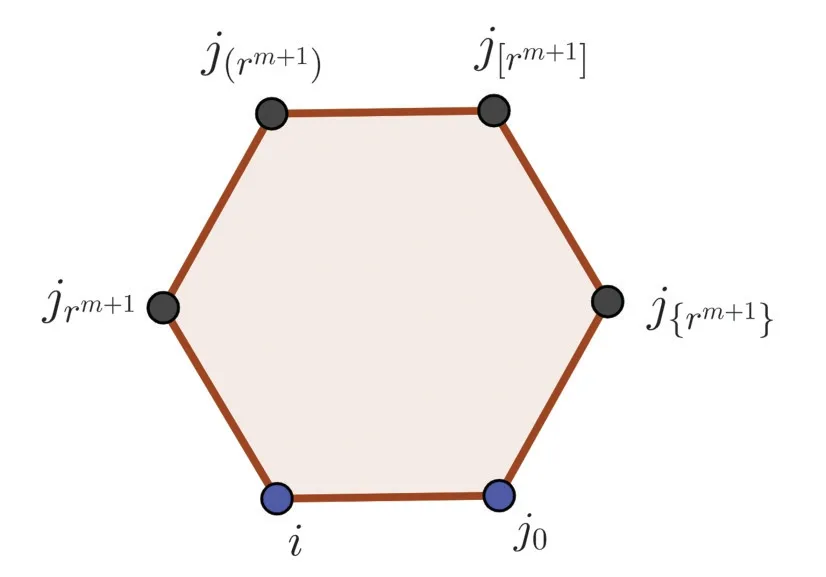
图2 Wn(G)的部分图
当连边ij0是jrm+1的父边时,有

同样地,有
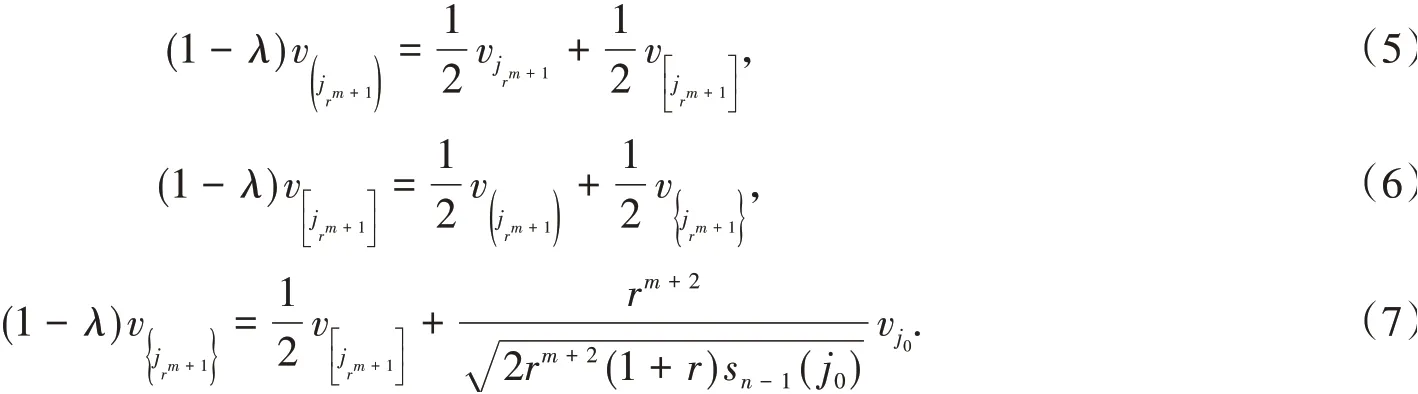
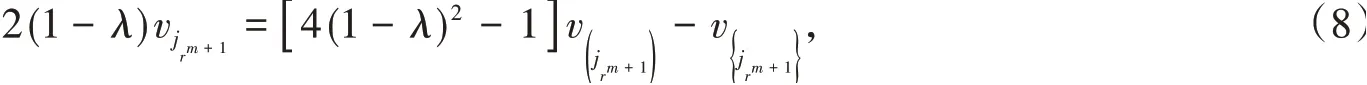
其中λ≠1.
联立式(5)和式(7),消去v得
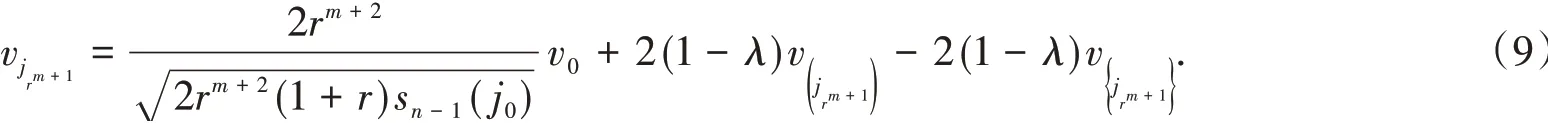
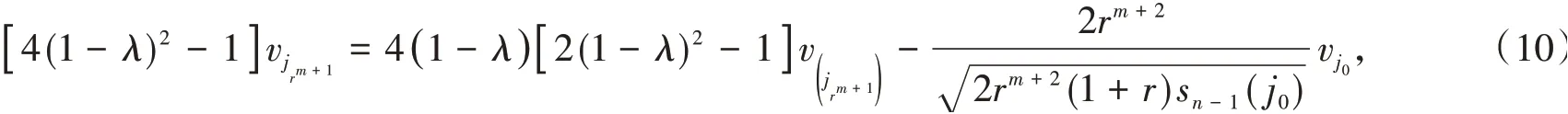
其中λ≠1.
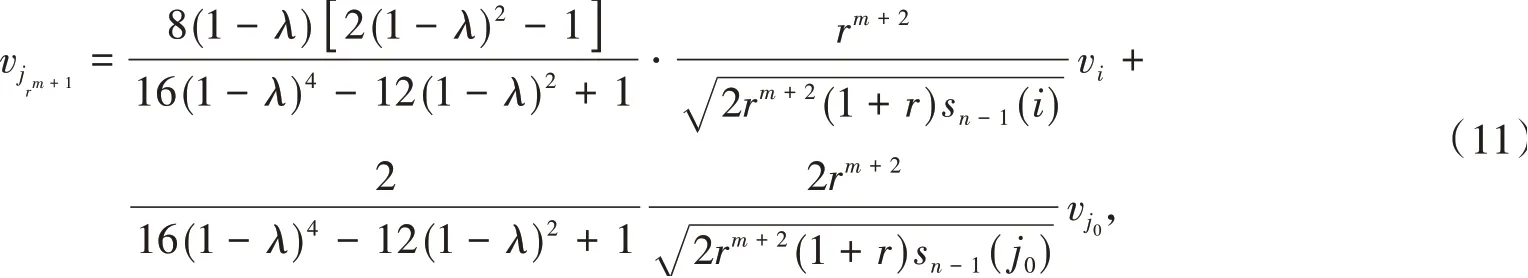
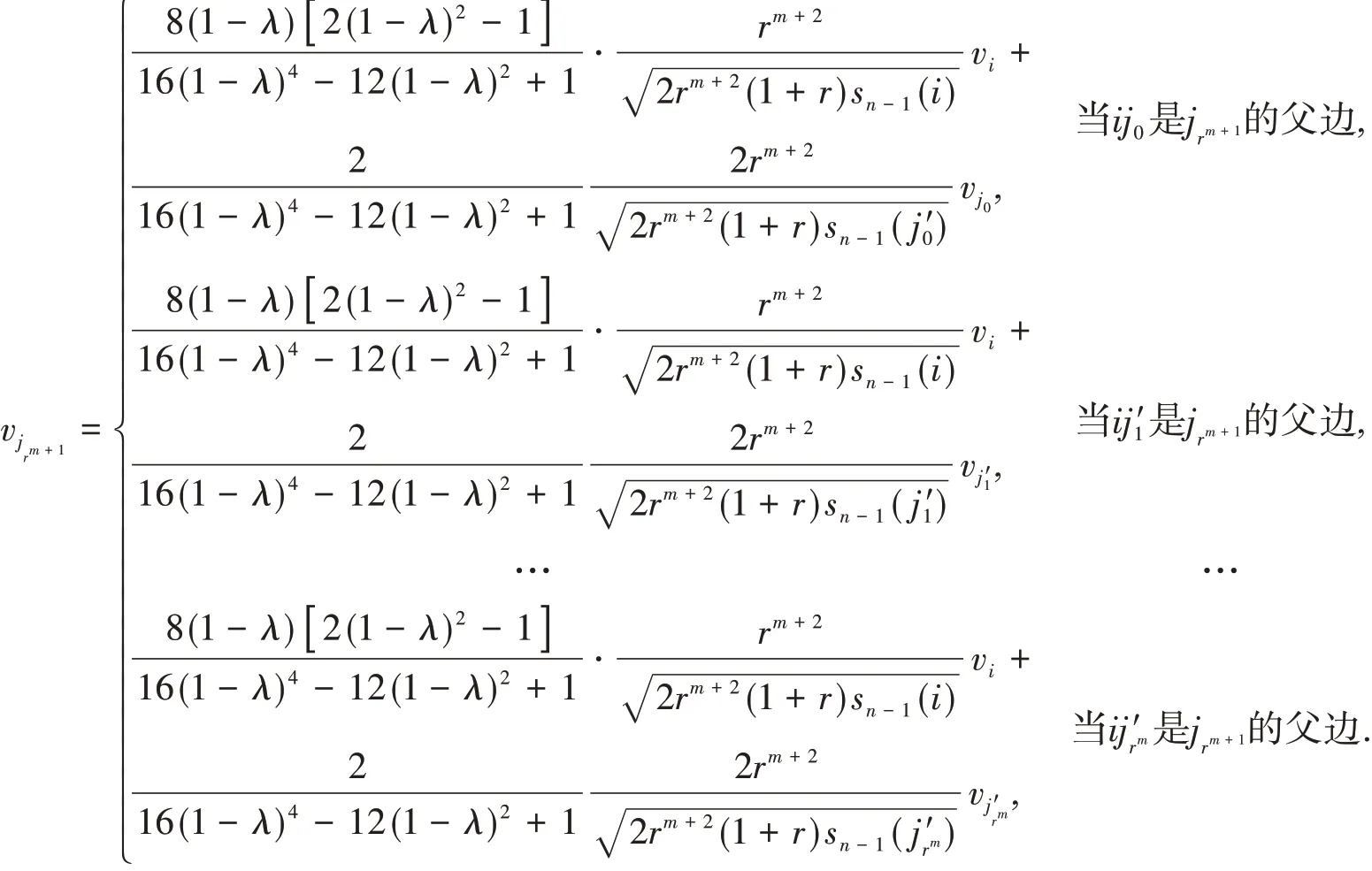
当ij′rk-1是jrk的父边时,k=m+2,m+3,…,n-1,
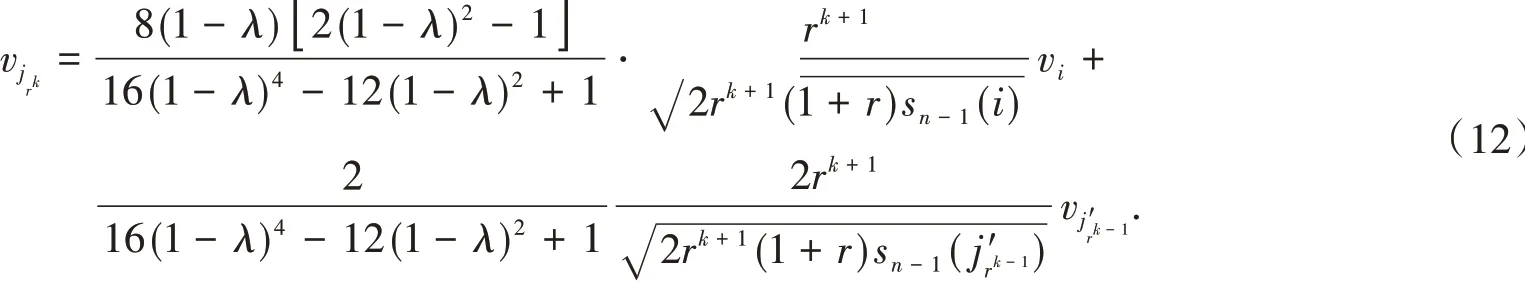
将式(12)代入式(3),得
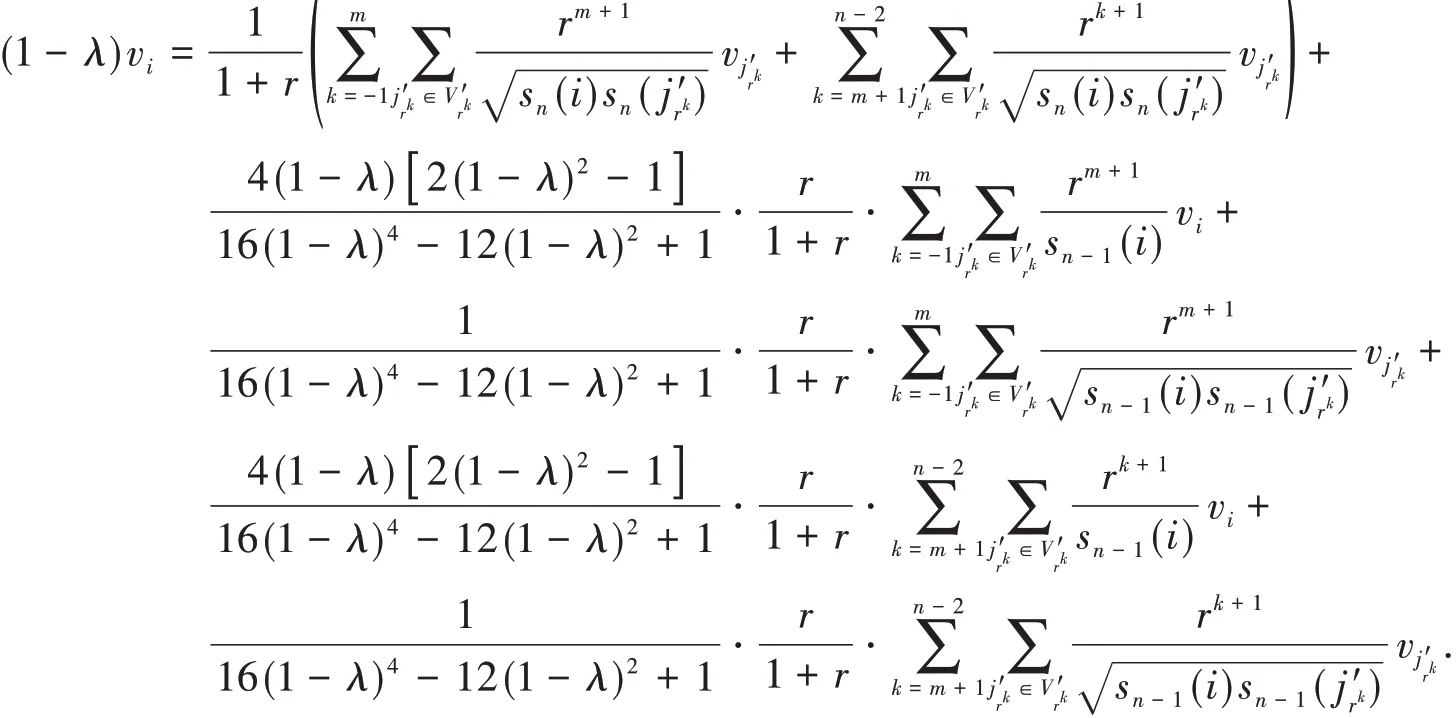
又因为
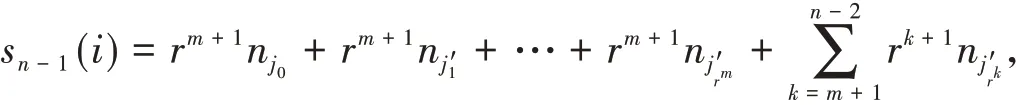
所以
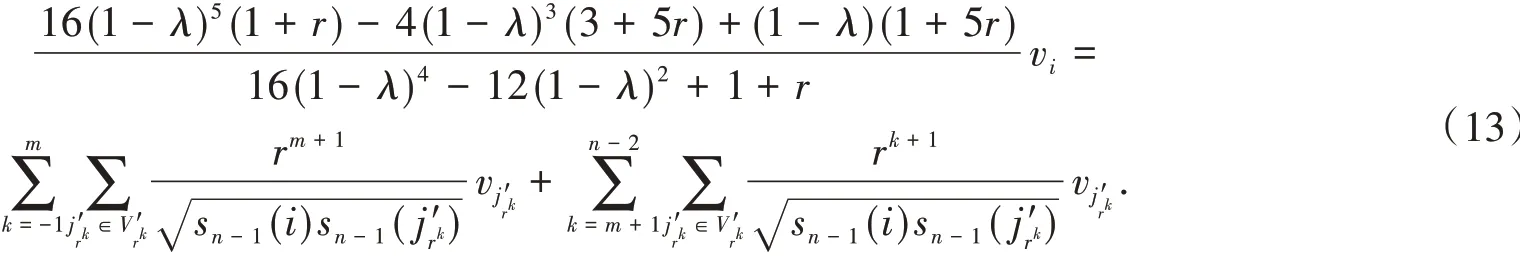
由式(13)可得前一代网络的标准邻接矩阵的特征值,即

是Pn-1的特征值,记作,则
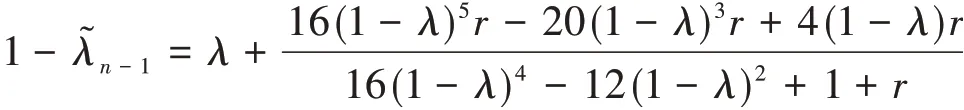
是Ln-1的特征值,记作λn-1.
最后考虑特征值的重数:易知mLn-1(λn-1)≥mLn(λ).假设mLn-1(λn-1)>mLn(λ),则存在Ln-1的属于λn-1的特征向量,使其与Ln的属于λ的特征向量无关,但是根据式(12)不存在这样的特征向量,所以mLn-1(λn-1)=mLn(λ).证毕.
如果从第n-1代入手,依据定理2.1,反解方程,得到第n代的特征值,即定理2.2.
定理2.2 设λ为Ln-1的任意一个特征值,λ≠1,r(0<r<1)为权重因子.若fi(λ),i=1,2,…,5是方程
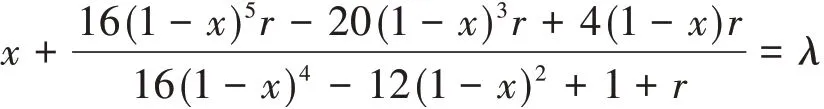
的解,则fi(λ)是Ln的特征值,且mLn(fi(λ))=mLn-1(λ),i=1,2,…,5.
证明 由定理2.1直接得到.
根据韦达定理,有
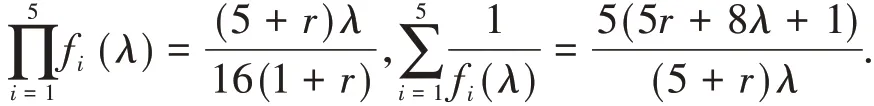
网络的谱是所有的特征值的集合,因此,第n代网络的谱可以通过前一代找到,得到定理2.3.
定理2.3 设网络Wn(G)(n≥1)的标准化拉普拉斯谱是σn.
(1)当Wn(G)是二分图时,

(2)当Wn(G)不是二分图时,
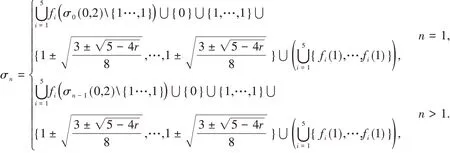
证明 首先,网络Wn(G)(n≥1)是连通的,所以0是网络的标准拉普拉斯矩阵Ln的一个特征值.
其次,因为网络是二分图当且仅当网络中不存在奇数环,已知网络Wn(G)(n≥1)是由许多个六边形和初代图G构成,六边形是偶数环,所以仅通过初代图能判断该网络是否为二分图,分为两种情况.当Wn(G)是二分图时,2是Ln的一个特征值.
进一步,解16(1-x)4-12(1-x)2+1+r≠0,得到于是根据定理2.2,Ln的大部分特征值,除了1和都可以由Ln-1的谱获得.因此,存在Ln的特征值不能由Ln-1的特征值获得,它一定是1和此外,Ln-1的每个特征值都会生成Ln的5个特征值,即fi(σn-1),i=1,2,…,5.
最后,整理即证.
3 结论
复杂网络的特征谱逐渐引起人们关注.网络的谱是所有特征值的集合,特征值的计算问题是谱研究的重要问题之一.网络构成越复杂或网络规模越大,所需计算的难度越高.本文构造了一类自相似网络——加权迭代六边形网络,通过分析和计算得到精确的拉普拉斯谱的结构式.网络的谱不仅可以用来分析网络结构,还可以进一步揭示网络的功能特性,甚至在网络的动态过程中起到重要作用.

