基于向量节点约束建模的输电网弹性供电预测模型

邹健，谢益峰，舒能文

(国网浙江海盐县供电有限公司，浙江,海盐 314300)

0 引言

可再生能源和新能源发电并网不断发展，给电力系统带来了巨大的冲击和挑战，致使在用电需求固定时，电力过剩现象变得越来越严重，导致大规模电力资源被浪费[1-2]。因此，输电网弹性供电预测技术应运而生。

文献[3]提出了基于模式匹配的输电网弹性供电预测模型，采用随机森林决策方法，建立供电负荷匹配规则，构建供电预测模型，该方法具有较高的预测计算效率，但该方法的预测精度较低。文献[4]提出了基于深度置信网络的输电网弹性供电预测模型，以输电网相关设备配置的动态频率作为深度置信网络的输入特征值，得到输电网弹性供电的预测结果。该方法能够稳定控制扰动后系统动态频率，但该方法存在预测误差较大的问题。

针对上述方法的不足，提出并构建基于向量节点约束建模的输电网弹性供电预测模型。通过两个预测点维度的总和计算预测距离。根据相似性自连接操作删选数据，引入向量节点约束连接法，计算输电网弹性供电预测区域。考虑多指标对电力发展弹性系数的影响，依据非线性高维识别特性，构建电网弹性供电预测模型，有效计算弹性系数，减小预测误差，提高预测精度。

1 预测区域确定

为了获得准确输电网弹性供电的预测结果，确定预测区域。将供电区域划分为邻居单元格，计算供电点与邻居单元格之间的距离，在二维距离上完成维度总和计算，确定预测距离。在MapReduce架构下，通过四阶段删选输出可行距离方案，采用向量节点约束确定最佳预测区域。

1.1 距离计算

在计算供电点至邻居单元格之间距离的过程中，先定义如图1所示的NC邻居单元格。

图1 NC邻居单元格示意图

当计算q和C00之间距离时，因q位于的C11和对应单元格C00分别在两个维度上均不同，由此要具体计算q至C11之间实际距离，必须考虑两个维度总和，则维度总和MindistCell的计算表达式为

(1)

式中，d和i均代表单元格数据量，c代表邻居单元格，q[i]代表主单元格中指定的出发节点，lbc[i]代表c的下界，ubc[i]代表c的上界，p代表向量节点空间总维数[5]。

1.2 删选方案

在完成距离计算后，使用分布式的MapReduce架构进行方案删选。第一阶段中，计算选定节点至单元格之间的距离，详细见图2，其中指定节点是q。

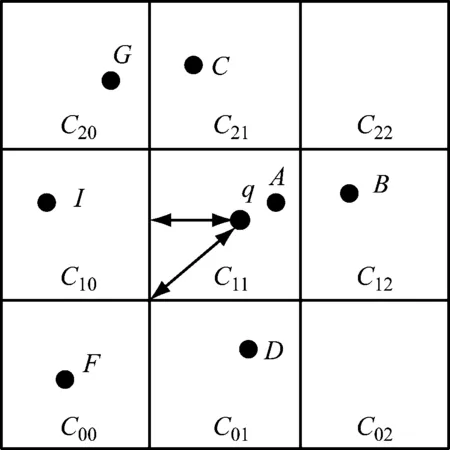
图2 点至单元格间距离

在第二阶段中，主要是对出发点所处约束区进行删选。距离q与节点A呈线性关系，因此在负荷点至邻居单元格之间距离约束下，邻居单元格到A点之间距离是阈值ε的约束区域，见图3。

图3 A点所处约束区示意图

第三阶段主要是执行单向边的删选方案。图3中，忽略阴影部分，在单向边删选之后，输出结果的为{B,C,D;A}。

1.3 结果选择

以上的Map阶段操作结束后，把获取的结果集合传输至Reduce，实现路径连接，全部设定情况如图4所示。则获取的结果集合为{A,B,G;A,C}、{A,F;A,D}。当删除出发点之后获取{G,B;A,C}、{F;A,D}，分号前为后续步骤要调用的备选点，分号后为已经遍历过的路径[7]。按照上述思想迭代调用Map输出结果集合，直到获取所有约束连接路径集合。

图4 路径选择示意图

2 输电网弹性供电预测

在上述预测区域确定之后，利用支持向量机，结合弹性系数与投入产出，实现输电网弹性供电预测模型构建。详细过程如下。

(1) 构建弹性系数模型

假设x代表自变量，y代表x的可微函数，则y对x的弹性系数表示形式为

(2)

(2) 输电网需求的弹性投入-产出模型构建

假设VGDP(t)、VGDP(t+1)分别代表相邻2a的生产总值，E(t)、E(t+1)分别代表对应的电力需求[8]，则GDP增长速度计算式为

(3)

用电量增长速度(%)计算式为

(4)

其中，εyx表示用电量增长影响因子。

电力弹性系数计算式为

(5)

(3) 基于历史数据预测用电量

使用支持向量机对电力需求影响进行模拟，并构建基于历史数据的用电预测模型。计算公式为

(6)

其中，r代表误差率,Y*表示需求用电量，Y代表历史年用电量。

3 实验结果与分析

为了验证所构建预测模型的整体有效性，将基于向量节点约束建模的输电网弹性供电预测模型用在某区域电网规划中，该区域电网主要为66 kV和10 kV。在实验中，将所构建模型与基于模式匹配的预测模型、基于深度置信网络的预测模型进行对比验证。

3.1 弹性系数计算

弹性系数对输电网弹性预测结果有较大影响，弹性系数越准确说明预测结果越精准。3种方法的弹性系数计算准确性对比结果如图5所示。

图5 弹性系数计算结果

分析图5可知，随着供电时间的不断增加，所构建模型的弹性系数计算结果与实际结果较为接近，可准确计算弹性系数。

3.2 预测效果

实验区域的用电量负荷情况见表1。

表1 实验区域年度用电量预测结果

图6为不同模型用电量预测仿真效果图。

图6 不同模型用电量预测仿真效果图

根据图6可知，所构建模型的用电量预测结果与实际用电量结果较为接近，数值结果相差较小。

实验中，预测结果的平均相对误差计算式为

(7)

表2 不同时间输电网弹性供电预测误差均值

分析表2可知，在不同用电时段中，所构建模型的预测误差均小于2种对比模型。

4 总结

本文提出并构建基于向量节点约束建模的输电网弹性供电预测模型，精准计算预测区域，引入支持向量机结合弹性系数与投入产出，对输电网弹性供电进行预测。通过实验对所建模型进行验证，结果表明，该模型能够准确计算弹性系数，且最小预测误差仅为0.76，能够满足输电网弹性供电的预测需求，具有较高的可靠性。