关联成像算法研究进展

林惠祖,刘伟涛,孙帅,杜隆坤,常宸,3,李月刚

(1国防科技大学理学院,湖南 长沙 410073;2国防科技大学量子信息学科交叉中心,湖南 长沙 410073;3北京邮电大学电子工程学院,北京 100876)

0 引言

成像是信息获取的重要手段,是人类认识和改造世界不可或缺的有力工具。传统成像通过透镜建立了基于高斯成像的物面到探测面的“点对点”对应关系。对于二维图像信号,需要用面阵探测器来获取图像信息,是一种“所见即所得”的直接成像模式。随着人类对成像分辨率和成像视场要求的不断提高,成像系统的复杂性和实现难度将非线性地增加。近年来,随着量子纠缠和量子光学原理的产生,在光场调控和量子探测技术支撑下,关联成像逐步发展起来[1−7]。作为一种基于光场涨落和二阶关联获取物体图像的新型成像技术,关联成像不仅具有更高的信息获取效率,而且提升了图像信息获取方式的灵活性,能够具备传统成像所不具备的成像能力,如非局域成像、无透镜成像等,在高分辨率成像、高灵敏度成像和抗干扰等方面具有优势,受到了国内外学者的广泛关注。随着关联成像研究的逐步深入,人们实现了基于(赝)热光的鬼干涉[3]、亚波长干涉[8,9]和傅里叶成像[6],关联成像的思想也被逐步用到X光[10−13]、太赫兹波[14]、微波[15−17]等其他领域,甚至利用电子[18]、原子[19]、中子[20,21]等物质波实现了关联成像。关联成像的研究也在逐步向应用拓展,研究人员分析了散射[22]、湍流[23,24]、相对运动[25−27]、背景光[28]等实际条件对成像性能的影响。

与传统的基于高斯成像的“点对点”图像获取模式不同,关联成像是一种物面到探测面“多对多”的新型成像模式,需要通过计算来重构“点对点”对应关系,进而获取目标图像信息。它是一种“所见非所得”的间接成像模式,计算成为成像过程的必备要素,因而关联成像算法在图像的获取过程中起着举足轻重的作用,是提高成像质量、提升成像效率的重要手段。好的关联成像算法对于推进关联成像的实际应用进程具有重要意义,不仅能大大降低成像所需的测量次数,减小采集的数据量,提高信息提取效率,缩短成像时间;还能减小非完全采样带来的统计误差与各种不良干扰的影响,提高图像重构质量;且能降低对成像硬件的要求。随着关联成像技术研究的逐步深入,关联成像算法也不断发展。本文将从关联成像的原理机制出发,梳理关联成像算法的发展历程,对其基本原理、优缺点和适用场景进行分析,以期为关联成像算法的优化和新算法的提出提供一定参考。

1 关联成像基本原理

1.1物理原理

关联成像利用光场的高阶关联获得物体的图像信息,其结构示意图如图1所示。在关联成像系统中,赝热光源一般由单模激光经过旋转毛玻璃、空间光调制器或数字微镜阵列调制后产生。赝热光源被分为两路:一路经过物体后的总光强被一个点探测器收集(孔径内能量被透镜收集至一点,这种探测方式也称桶探测),称为物臂;另一路经自由传播或透镜成像后的光强分布被面阵探测器记录,称为参考臂。物体的图像可以通过两臂信号的关联计算得到。由于这种成像方式有悖于常规思维习惯,该成像方式在被发现之初就被冠之以“鬼”成像的称谓。与直接记录物体信号光强度分布的传统成像相比,由于采用了照明或后端调制编码、桶探测和关联重构图像等方式,关联成像具有编码设计灵活、灵敏度高、抗噪性强等显著特点[29−34]。同时,关联成像可以结合压缩感知、机器学习等方法,突破奈奎斯特采样定律的限制,实现亚采样下的图像重构[35−44]。但是由于关联成像利用点探测器来实现对面目标的成像,需多次测量来获取目标信息,且成像场景越复杂,获得高质量图像所需的测量次数就越多,这样会严重增加图像重构所需的数据采集时间和数据量。

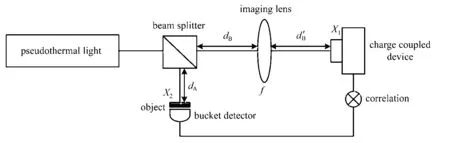
图1 关联成像结构示意图Fig.1 Structure diagram of ghost imaging

赝热光关联成像的原理可以用Klyshko提出的“Advanced wave”理论来解释,将图1的光路等效展开,如图2所示,可给出类比于高斯透镜成像的几何成像图及成像公式[45,46]。由光源发出的光经过分束器,两光子传播相同的距离后在两个面上形成完全相同的空间分布,形成这两个面上的“点对点”对应关系。将光源看作相位共轭镜,由物体发出的光经过光源后获得共轭相位,从而在光源的对侧得到物体的图像,再经透镜成像到CCD相机的探测面上。由以上解释可以看出,关联成像利用光子对建立了类似于传统成像的“点对点”对应关系。

图2 赝热光关联成像展开图[46]Fig.2 Unfolded picture of the ghost imaging system with psudothermal light[46]

由于关联成像中物体的图像信息是通过物臂端测量得到的总光强信号和参考臂端得到的散斑场进行关联运算得到,传统的关联成像算法(TGI)可写为

式中:〈·〉表示时域上的系综平均,实际应用中对应多次采样;I1(x1)表示参考臂光强分布;B表示桶探测信号,可表示为

式中:I2(x2)表示物体表面的光强分布,T(x2)表示物体的强度反/透射率函数。将(2)式代入(1)式,可以得到

(赝)热光场可以看作是足够多的随机相幅矢量的叠加,光强服从高斯随机变量的统计性质,有

当照明光场平均强度均匀时,在足够多的采样次数下,(4)式右边第一项为热光二阶关联的背景项,不包含物体信息;第二项为其关联项,在一定条件下可以近似写成δ函数。此时,再结合(3)式可以看出,物体强度反射率函数和光场关联函数的卷积实际上决定于物体的反射率分布,这就是关联成像的结果。

对应于光场相干度的定义,也可以将关联成像的表达式写为

在照明光场平均强度均匀的条件下,(5)式和(1)式是等效的,相同次数下获得的图像质量也相当。将(2)式代入(5)式,可得

1.2数学表示

由以上分析可知,计算是关联成像的必要部分,建立与图像获取相对应的数学表示显得尤为重要。无论是“点对点”还是“多对多”的成像模式,图像获取都可以表示为如下求解问题模型

式中x∈RN为待恢复的图像信号,y∈RM为探测信号,Φ∈RM×N为测量矩阵,ε为探测噪声,如图3所示。当成像模式为传统的“点对点”时,M=N;当成像模式为“多对多”时,M可以小于N。理想情况下,在传统成像中Φ为单位方矩阵。此时,探测器上一个像元的探测结果直接对应物面上一点,如图3右上图所示。对于“多对多”成像模式来说,探测器上一个像元的探测结果是物面上多点探测的线性组合,如图3右下图所示。关联成像作为一种“多对多”成像模式,测量矩阵Φ为M次测量所得参考臂相机信号构成的随机矩阵,每一行即为一帧参考臂相机信号,y为点探测器的探测信号,而计算二阶相干函数就是计算ΦTΦ,其中T表示矩阵的转置。当光源随机照明时,Φ为随机矩阵,ΦTΦ相当于一个全1矩阵加单位矩阵。为了更好地求解(7)式的问题模型,即在含噪的条件下高效地恢复图像信息,减小重构误差,人们从光源设计[29−31]、探测方法[47,48]、成像策略[32−34]、算法优化[35−42]等角度入手展开研究。其中,关联成像算法在一定程度上决定了重构图像的质量以及系统的工作效率,因而成为关联成像技术走向实用化的关键,研究高效的关联成像算法是提高成像质量和成像速度最有效的方法之一。

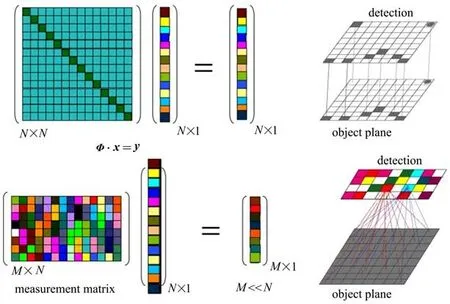
图3 不同成像模式的图像采样方式Fig.3 Sampling methods for different imaging modes

由于关联成像需要对探测数据进行处理、运算才能得到物体图像,这也给借助算法提升关联成像性能带来了可能。关联成像算法研究的主要目标是提升图像质量和减少成像的资源消耗。基于关联成像系统的物理机理、统计解释和数学表示,关联成像算法的研究思路主要有以下两类:一是从强度关联算法中各要素的物理意义出发,改进算法来克服不良条件对图像重构的影响,包括涨落关联算法、差分关联算法、归一化关联算法和二阶关联归一化算法等;二是从数学表述形式出发,寻找更优的数学求解模型来提升系统性能。由此,人们发展出一些矩阵求解方法,包括伪逆算法和压缩感知算法等。同时,机器学习等领域的新发展也给关联成像算法研究带来了新的思路。下面将系统介绍这几种关联成像算法,并对其优缺点和应用场景做一定的讨论。

2 关联成像算法

2.1基于光场关联函数的改进算法

2.1.1 涨落关联算法

关联成像是通过统计的方法来重构物体图像的,TGI算法通过物臂端测量得到的总光强信号和参考臂端得到的散斑场进行关联运算重构出目标图像,如(1)式所示,但根据该式计算得到的图像结果往往对比度不高。为了提高图像对比度,通常结合物理上对于关联的理解和涨落的定义,(1)式可以改写为

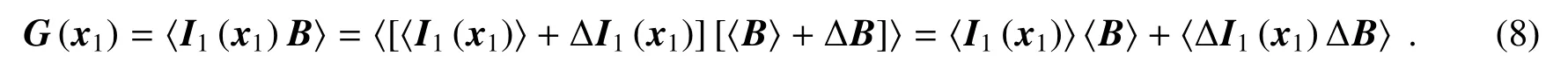
理论上,当采样次数无限多时便可以得到图像期望值。而在有限的测量次数下,重构的图像中存在相对于期望值的统计误差。在有限采样次数下,(8)式右边第一项是背景项,且和照明光场平均强度的空间分布有关,并不是常数项,被减去之后可以提高成像质量。利用强度关联减掉背景项的方法称为背景减除的传统关联成像算法(BSTGI),可以表示为

在相同采样次数下,(9)式比(1)式重建图像的信噪比高。由(9)式可见,减去背景项后,剩余部分实际上表示了两光场的涨落关联,即图像是由两探测器的涨落之间的关联得到的,因此BSTGI算法也被称作关联成像的涨落关联算法。

将(2)式和(4)式代入(9)式,可得

2.1.2 差分关联算法

在关联成像系统中,当目标为透明度高的透射型物体或反射面占比高的反射型物体时,由于回波平均强度大而相对涨落小,难以有效获得光强的涨落,成像质量较差。为解决这一问题,2010年,Ferri小组提出了差分鬼成像算法(DGI),其在TGI算法的基础上引入了差分项,DGI算法在每次采样过程中将参考臂端数据求和,作为“桶探测器数据S”引入关联运算,实验架构如图4所示[35]。DGI算法可以表示为

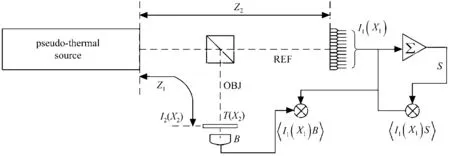
图4 差分关联成像实验架构图[35]Fig.4 Experimental architecture of DGI[35]

(11)式可变形为

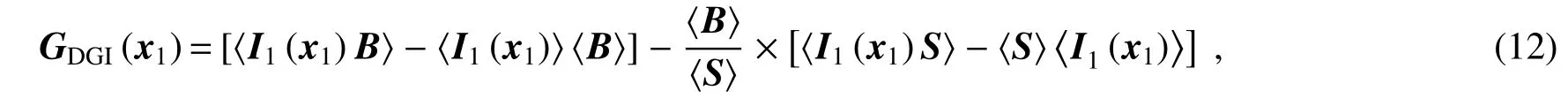
式中:前两项之差是涨落关联算法获得的物体的图像,后两项可以看作整个视场的像。因此DGI算法可以表示为

令χ=T/M表示物体面积和视场面积之比,χ≤1。此时(13)式可简化为

式中等号右边两项分别对应物体和整个视场的强度关联图像。这两幅图像是基于相同散斑序列照明重构得到的,是相同的独立同分布的变量之和,因此等号右边两项是正相关的。通过两项做差可以抑制物体关联图像中的统计噪声,因而可以突破散粒噪声极限,获得高信噪比的图像,如图5所示[35]。图5是在相同采样次数下,DGI算法和TGI算法在不同物体反射系数条件下的成像质量对比,其中横坐标和物体反射系数有关,横坐标越接近1表示物体反射面积越少;纵坐标表示成像质量。由图5可见,系数χ越接近1,对应物体越接近全(透)反射,(14)式两项的统计误差越接近,DGI算法相比于TGI算法越能更好地抑制统计误差,图像信噪比越高。

图5 DGI算法和TGI算法成像图像质量对比[35]Fig.5 Comparisons of image quality between DGI algorithm and TGI algorithm[35]

2.1.3归一化关联算法

DGI算法解决了大物体成像质量差的问题,但其仍然基于照明光场平均光强空间均匀的假设,当照明光场平均强度不均匀时,图像质量会受到影响。为了解决这一问题,2012年,格拉斯哥大学研究小组在DGI算法的基础上提出了归一化关联成像算法(NGI)[36],NGI算法和DGI算法的关系可以表示为

在照明光场统计性质均匀的条件下,NGI算法和DGI算法的性能相当,下面讨论光场统计性质不均匀的情况。当赝热光场强度的一阶矩(平均强度)和二阶矩(强度涨落)在空间上分布不均匀时,照明光场可表示为

式中ς(x)表示光场平均强度的不均匀系数,其不随时间发生变化。此时光场的一阶矩和二阶矩分别表示为

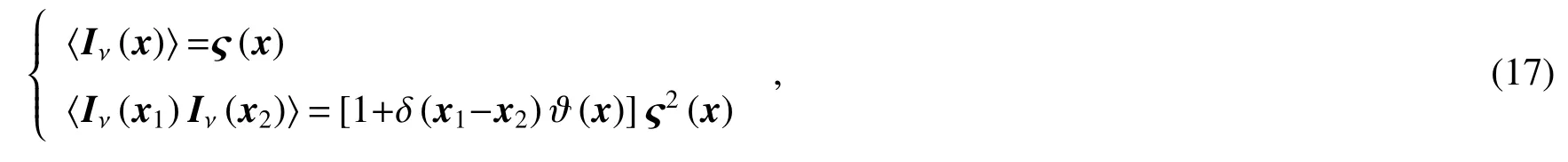
式中ϑ(x)表示光场强度涨落的系数,ϑ(x)≤1。对于理想的赝热光场,ϑ(x)=1。将(2)式和(17)式代入(11)式,得到

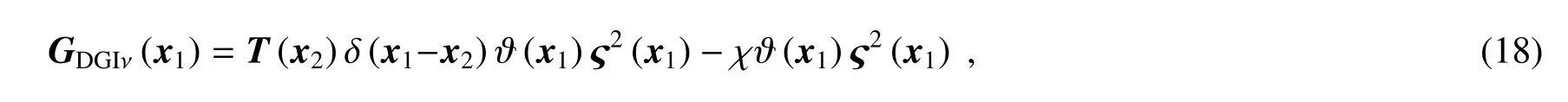
可以看到,当光场强度的一阶矩和二阶矩不均匀时,得到的物体图像也不均匀。将(17)式和(18)式代入(15)式,得到

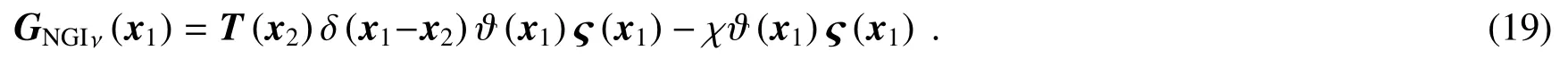
可见与DGI算法相比,NGI算法在参考臂记录总光强值并用来归一化物臂端测得的总光强信号,可以抑制光场强度一阶矩,即平均光强分布的影响,但无法抑制光场强度二阶矩的不均匀对成像的影响。

2.1.4二阶关联归一化算法

根据前面的讨论,照明光场的二阶相干度对应于关联成像系统的点扩展函数。在实际应用中,通常用旋转的毛玻璃调制一束激光产生赝热光作为照明光场,光场的平均强度分布将是高斯分布。不同时空点的光强不满足全同分布条件,且光场的近场涨落分布也不均匀,这些因素都会影响关联成像的点扩展函数,进而影响成像质量。为了解决这一问题,Sun等[37]提出了二阶相干度归一化算法(SGI)。SGI算法的基本思想是对光场二阶相干度进行归一化,可表示为

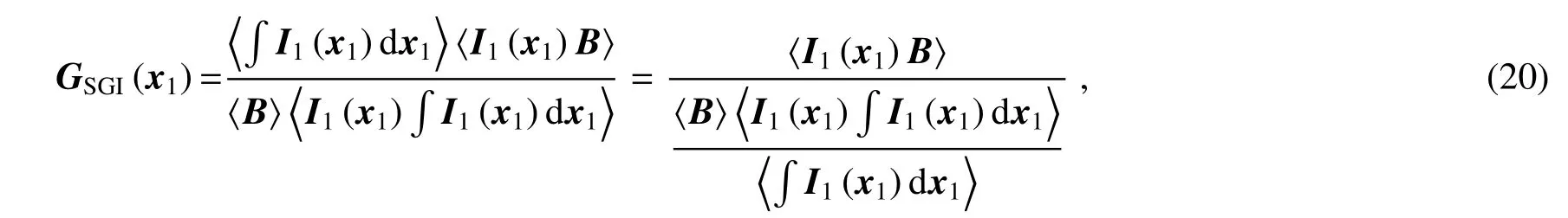
式中分母可以看作是视场的关联图像,分子则是TGI算法得到的物体图像,两者的统计误差有关联。与DGI算法通过将两者统计误差作差来提高信噪比不同,SGI是通过将两者统计误差相除来提高信噪比。(20)式还可以表示为

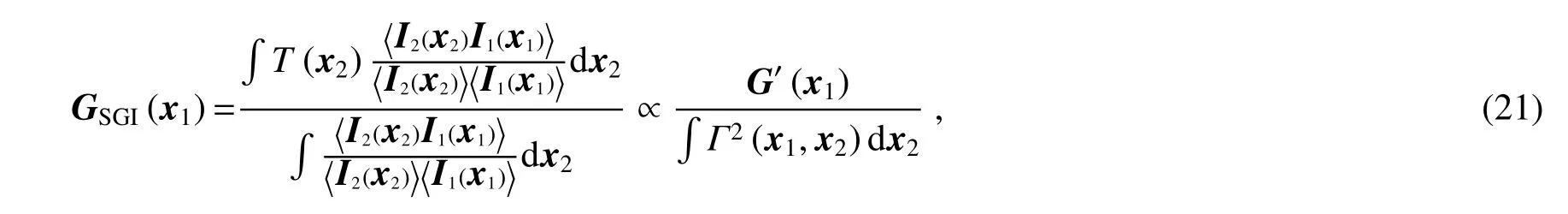
式中分母可以看作照明光场的二阶相干度。SGI算法可以看作在TGI算法基础上对照明光场的二阶相干度做了归一化。当光场强度的一阶矩和二阶矩空间分布不均匀时,将(2)式和(17)式代入(21)式,得到

式中分子和分母的第一项都是背景项,不包含信息。在关联成像中,物臂和参考臂光场统计性质相同,即ϑ(x2)=ϑ(x1)。对比(18)、(19)式和(22)式,在SGI算法中,光强的不均匀系数对成像质量的影响通过归一化消除,同时强度涨落系数ϑ(x1)的影响也被缩小。当χ≈1,即物体越接近全反或全透,此时涨落系数ϑ(x1)对成像质量的影响也被消除。通过以上分析可以看到,SGI算法通过对关联成像中光场二阶相干度的归一化,有效抑制了光场一阶矩(平均强度)、二阶矩(涨落)分布不均匀和光源功率抖动对成像质量的影响,可以得到比DGI算法和NGI算法成像质量更高的图像。

上述算法从光场关联函数出发,以提高不同条件下的成像质量为主要目标,都属于线性算法,运算速度较快且对软硬件的要求不高。为了在提高成像质量的同时减少成像所需数据量和提高成像分辨率,人们从关联成像的数学表述形式出发,发展出一些矩阵求解方法。

2.2基于矩阵的求解与改进

2.2.1 压缩感知算法

压缩感知(CS)[49,50]又称压缩采样,作为新的采样理论,其利用信号的稀疏特性,可在远小于Nyquist采样率的条件下用随机采样获取信号的离散样本,然后通过非线性重建算法完美地重建信号。关联成像从数学形式上来看与压缩感知方法极为相似,赝热光场的空时随机涨落和桶探测器的使用完成了CS方法中所需的“随机+整体”测量,因此CS方法可以自然地应用在关联成像数据处理中,计算型关联成像更是被看作CS在成像领域中的一种具体物理实现方式。基于关联成像与CS在数学形式上的共通性,可以很好地把CS应用到关联成像的数据处理中以减少数据量和提高成像分辨率。2002年,Rice大学的Baraniuk小组将CS应用于光学成像,实现了“单像素相机”[50]。2009年,Silberberg小组提出的基于CS的关联成像算法(CGI)将CS引入关联成像中,可以在较少的采样次数下重构出优于一般关联成像算法的图像,提高了关联成像的信噪比和分辨率[38]。2011年,Boyd小组的Zerom等[51]利用纠缠光子对采用CS的方法实现了单光子水平的高分辨关联成像。2012年,中国科学院上海光学精密机械研究所的Gong等[39]采用CS算法在欠采样条件下实现了高分辨率的图像获取。

CS理论的实现条件主要包括两点:信号的稀疏性和测量矩阵的不相关特性。信号的稀疏性也是数据压缩的基础,自然图像大多满足稀疏性(或可压缩性)或是在某个变换域下近似稀疏。CS理论表明:如果被探测的信号具备稀疏特性,则获取信号所必需的测量数据可远小于信号的维数。此时,由于观测方程的数量小于未知数的数量,(7)式所示的信号重构问题是一个欠定问题,或者称为病态问题,要准确恢复信号必须增加其他的正则约束条件。若测量矩阵满足有限等距性质(RIP),则可得到一个最优解。满足RIP性质意味着信号恢复具有稳健性和鲁棒性,而关联成像的随机测量矩阵正好能够很好地满足RIP性质,因此CS算法在理论上可精确求解(7)式,可以以更少的采样重构质量更高的图像。

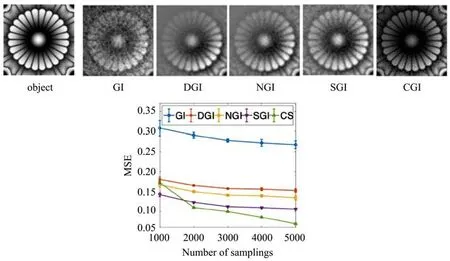
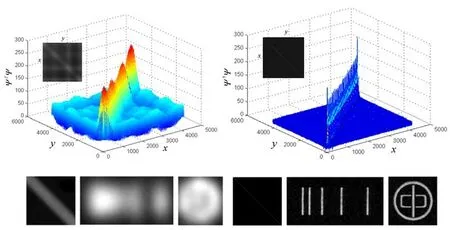
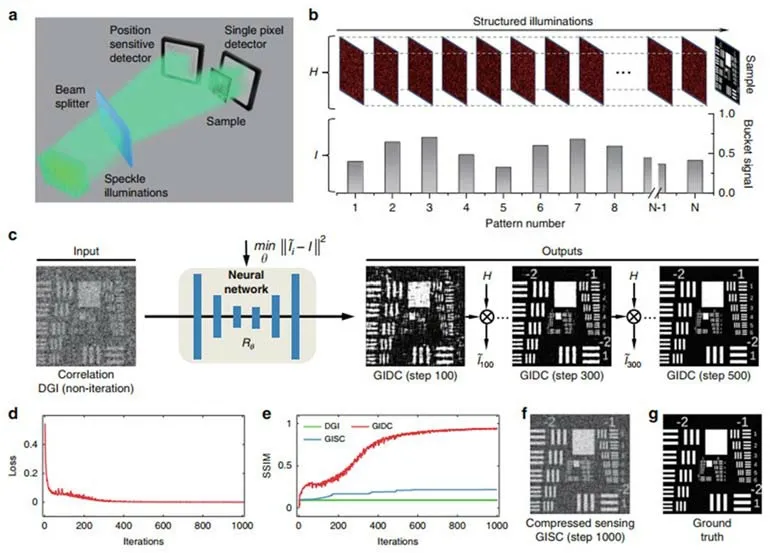
根据线性代数理论,当M

图像稀疏性最本质的度量为l0范数,若测量中含有噪声,则Find sparsestx,s.t.y=Φx的数学描述为

式中参数σ反映了测量噪声的水平。

随着问题维度的增加,求解该问题的复杂度将指数增长。对于很多的测量矩阵(如随机矩阵)来说,当信号足够稀疏时,l1最小化问题完全等价于l0最小化问题。CS理论创造性地将l1范数最小化稀疏约束与随机矩阵结合,得到一个稀疏信号重建性能的最佳结果。最小l1范数模型求解是高效、稳健且适合图像重构等大规模数据计算的稀疏优化算法。

基于l1范数凸优化的稀疏重构模型为

式中∥∥2为二阶范数,为一阶范数,(24)式为基追踪去噪(BPDN)问题。处理实际问题时,通

过

对系统测量条件的分析可以得到噪声水平的大致估计。实际求解形如(24)式的约束优化问题时,可将约束条件转换为惩罚项,构造非约束优化问题其中x即为稀疏重构图像,τ为控制稀疏约束强度的参数。CS方法是求解该非约束优化问题的一种有效方法,它通过对稀疏信号的相对少数量随机投影的测量就可以获取信号的大部分信息,从而准确重构信号。虽然CGI算法可以实现较少采样下的高质量图像重构,但是也存在受光源功率抖动影响、受噪声影响大且计算时间随着成像帧数的增加而非线性地增加等不足,限制了CGI算法的实用性。

为了更好地说明和比较各个算法的性能,对光源功率存在抖动且照明光场不均匀实验条件下的TGI、DGI、NGI、SGI和CGI等各算法的图像重构质量进行了分析,并采用均方误差(MSE)指标来评价和比较各算法的成像质量[52],结果如图6所示。可以看到,在灰度物体图像的重构中,当TGI算法已经无法清晰重构物体图像时,DGI、NGI、SGI和CGI算法依然可以得到物体较高信噪比的图像,且CGI和SGI算法重构图像的均匀性优于DGI和NGI算法。

图6 不同算法的关联成像图像重构结果[37]Fig.6 Reconstruction results of ghost imaging with different algorithms[37]

2.2.2伪逆关联成像算法

上文介绍的CGI算法可在一定程度上提高关联成像系统的分辨率,但其局限于具有稀疏性的目标且运算时间较长。为了实现普适性的高分辨快速成像,发展出了伪逆关联成像算法(PGI)[40,41]。由(7)式可见,测量矩阵不是方阵,不存在逆矩阵,因此PGI算法在重构过程中对双臂间数据关联的计算方式做出调整,将参考臂光场替代为其伪逆矩阵,实验架构如图7所示[40]。

图7 PGI实验架构图[40]Fig.7 Experimental architecture of PGI[40]

PGI算法计算公式可表示为

式中:B为每次采样时的探测臂数据;I〈B〉表示与B同维度的矩阵,其值为B的均值;I为K×1单位矩阵;K为采样数;α为光强比例系数;Ψ=Φ−I〈Φ〉,Φ为采样所得参考臂数据整理得到的矩阵;Ψ†为Ψ的伪逆矩阵;O为物体。TGI算法中的ΨTΨ矩阵与PGI算法中的Ψ†Ψ矩阵和对应的图像重构结果对比如图8所示。在经过求伪逆矩阵变换后,Ψ†Ψ比ΨTΨ更接近一个标量对角矩阵,因此分辨率得以提升。此外,噪声也得到抑制,重构图像质量因此得以提升,且随着采样次数的增加,噪声抑制效果越来越好。但是在实际系统中,矩阵Φ和B往往存在一定误差,会严重影响Ψ†Ψ的真实结果,导致成像质量变差。

图8 GI中ΨTΨ矩阵(左)与PGI中Ψ†Ψ矩阵(右)和对应的图像重构结果[40,41]Fig.8 Matrices and reconstruction results ofΨTΨin GI(left)andΨ†Ψin PGI(right)[40,41]

2.3结合深度学习的关联成像算法

深度学习(DL)是机器学习研究中的一个新领域,它利用大量数据训练得到的神经网络来获得数据,例如图像、声音和文本等。近年来,随着数据量的急剧增长和计算能力的不断提高,深度学习技术迅速发展并应用到计算成像[53]的众多子领域中,一定范围内解决了相位恢复[54−56]、散射成像[57−59]、计算关联成像[60−63]等领域中长期未解决的问题。在基于深度学习的关联成像算法方面,大致分为两种:一种是对关联成像获得的图像进行降噪提质,在网络训练过程中输入大量的物体真实图像和关联图像,使得输出尽可能接近源图像,而在使用过程中先基于已有的关联算法获得图像,再利用神经网络进行质量提升;第二种则是基于关联成像的物理模型进行网络设计,以关联成像的照明光场和桶探测数据为输入进行训练,使用时直接由实验数据得到图像,不需要经过关联算法预处理。

2017年,中国科学院上海光学精密机械研究所的司徒国海小组利用训练好的深度神经网络感知模型对获得的关联图像进行降噪,提升了关联图像的衬噪比[61]。深度学习神经网络关联成像流程图如图9所示,包含训练和测试两个步骤,实验测试结果如图10所示,在成像采样率为5%的条件下能够实现对物体的恢复。但该方法存在训练数据难以获取且耗时的缺点,尤其是对更大视场的场景进行高分辨率成像时,所需训练数据的采集会更为困难。

图9 深度学习神经网络关联成像流程图[61]Fig.9 Flow chart of GI using deep neural networks[61]

图10 不同算法计算的图像重构结果[61]Fig.10 Reconstruction images using different algorithms[61]

关联成像通常需要进行大量的采样,这限制了成像系统性能,在处理运动物体时这一限制显得尤为突出。2020年,Hu等[63]通过使用数值数据训练卷积去噪自动编码器网络对少数样本中的模糊图像进行去噪,在采样率为3.7%的条件下还能获取图像信息。利用这些输出数据,通过基于关联成像的互相关方法重建运动目标的轨迹和清晰图像,所需的采样次数减少了三分之二。同时,结合了机器学习降噪的互相关运动物体追踪成像方法对运动物体的追踪成像有更好的表现。

此外,为了解决数据训练耗时问题和重建高分辨率图像,司徒国海小组于2022年提出了一种远场超分辨率的基于深度学习神经网络约束的关联成像技术(GIDC)[64]。GIDC使用随机初始化的神经网络约束鬼成像的计算重构过程,无需预先获取任何带标签的训练数据,仅需已知当前系统的探测信号和正向物理模型,然后利用该模型优化网络参数以拟合探测信号,获得优于传统方法的远场超衍射极限分辨成像结果,如图11所示,为远距离运动目标观测提供了一种新的途径。尽管GIDC也使用了神经网络,但并不存在标签数据获取和泛化性方面的问题,适用于重构不同结构类型的物体,具有普适性。

图11 GIDC整体框架[64]Fig.11 Sketch of GIDC[64]

3 结论

对关联成像算法进行了系统介绍,从基于关联成像机理的TGI算法出发,介绍了在此基础上发展而来的BSTGI、DGI、NGI和SGI等优化算法。其中,BSTGI算法可以一定程度上提升有限采样条件下的图像重构质量,但成像信噪比较低,尤其是高透射率的物体;DGI算法通过作差的方法来抑制有限次数采样下关联成像的统计误差,可实现大目标高质量重构,但成像质量受照明光场平均强度不均匀影响;NGI算法虽可以消除平均光强分布不均匀的影响,但无法抑制光场强度二阶矩的不均匀对成像的影响;SGI算法采用统计误差相除的方法,可以抑制统计噪声、光源的不均匀和光源功率抖动对关联成像的影响,使成像信噪比得到明显的提高。总的来说,这些算法的成像质量受光源参数、目标特性等因素影响较大,难以达到超分辨的效果。但这些算法都是线性算法,数据处理速度快,且更易于算法硬件化,有助于实现实时成像。为了进一步提高成像质量和分辨率,人们通过对关联成像图像求解模型的研究,发展出CGI和PGI等一些矩阵求解方法。这些算法不仅可以有效降低获得较高信噪比成像所需的采样次数,还有一定的超分辨成像能力。但CGI算法对噪声的鲁棒性相对较低,当采样矩阵或测量值中存在噪声时对成像质量影响较大,且图像重构时间较长,对运算设备性能有一定要求。同时,深度学习等领域的新发展也给关联成像算法研究带来了新的思路。深度学习技术可以通过大量数据训练实现端到端的自学习过程而非常适合应用于图像去噪等逆问题的求解,但在训练策略、训练时间和神经网络的普适性方面还有较大的提升空间。

基于上述关联成像算法,还有一些改进算法可以进一步提高成像质量,如伪逆迭代关联成像算法(PIGI)[65]、压缩感知归一化关联成像算法(CSNGI)[66]和基于二项式的关联成像重构算法(BGI)[67]等。目前,关联成像算法的研究在一定程度上解决了采样次数多、图像质量差等问题。总体而言,虽然线性算法计算速度快,鲁棒性较强,但在相同采样次数条件下成像质量一般不如非线性算法。而非线性算法计算时间较长,且对实验条件要求较高,否则无法获得高质量的图像。能够实际应用的算法应具有成像质量高、计算速度快、对外部噪声不敏感等特点,如何进一步开发或优化重构算法以提升复杂条件下的关联成像质量和成像速度,推进关联成像技术的实用化进程,这一关键问题显得越来越重要、越来越紧迫。此外,面向复杂环境或运动目标的图像获取等实际应用场景,为了提升信息获取效率,反馈式关联成像方法也得到了发展,如对感兴趣区域进行重点提取[34]、提取物体的位移或速度等信息以实现运动物体追踪成像[26,27]、利用前序测量调制后续照明光场[32]等。总之,随着关联成像研究和实用化进程的不断推进,关联成像朝着更远距离成像、更高质量成像、更快成像和更强鲁棒性成像的方向不断拓展,对高效、高速、高质量和易硬件化关联成像算法的要求将愈加凸显。