单像素复光场成像研究进展

郭 岩,何忆康,李显业,孙宝清

(山东大学信息科学与工程学院,山东 青岛 266237)

0 引言

光学成像是人类感知世界的重要手段,从人眼到相机、从显微镜到望远镜,不同种类的光学成像设备帮助人们感知、记录这个世界的不同尺度。但是,随着人类认知水平的发展,传统的点物成点像的几何光学成像机制已经难以满足人类对世界探索的需求,对高分辨、高维度、远距离、超快速成像机制的需求越来越迫切。传统的成像机制始终会受到衍射极限、成像器件、记录设备等物理机制的影响,难以在有限的尺度、较低的成本等条件下满足日益增长的探测需求,因此计算成像的概念应运而生。顾名思义,计算成像就是利用计算的方式,从有限的测量结果中重建出更高维度[1,2]、更大尺度[3,4]的成像结果。特别是最近二十年,计算机硬件水平得到了迅速发展,这极大地促进了计算成像理论的发展,一大批超采样定理[5]、超衍射极限[6]、超高速[7]、高光谱[8]的计算成像机制应运而生,展现出“大有可为”的发展趋势。单像素成像是计算成像的一个典型代表,不同于传统成像“大数据量”的发展趋势,单像素成像反其道而行之,仅仅采用一个没有空间分辨的“桶探测器”(Bucket detector),就可以实现二维乃至三维的数字成像,其一经提出就得到了学术界广泛的关注与讨论。得益于其对探测器分辨的超低要求,单像素成像技术在特殊波段成像[9,10]、超宽带脉冲信号采样[11]、光通信与加密[12]、极弱光成像[13]、无透镜成像[14]等领域有着广阔的应用前景。

广义上单像素成像最早可以追溯到逐点扫描成像,狭义上,在光学领域可以追溯到1995年,马里兰大学的Pittman与Shih课题组提出一种基于纠缠光源的单像素成像方案[15],其成像过程中具有空间分辨的参考光路未经过物体,而经过物体的光路仅被一单像素探测器探测,通过对偏振纠缠的双光子对的符合计数,即可获得物体的空间分布信息,因此被称为双光子关联成像。随着研究者对关联成像物理机制的研究,发现在热光条件下也可以实现类似的成像过程,特别是2008年Shapiro课题组采用一个空间光调制器(SLM)定制生成了照射在物体上的赝热光分布,节省了关联成像实验中的参考光路,这在光学上奠定了结构光编码单像素成像的基础[16]。因此,单像素成像又可以说是一种量子启发的成像方式。几乎与此同时,数学领域的研究者为了解释压缩感知的概念,构建了一个单像素相机模型[17],其通过一个数字微镜设备(DMD),将二维场景积分编码到一维探测序列上,利用压缩感知原理,在亚奈奎斯特采样要求的情况下获得了清晰的像[18,19]。单像素相机的提出极大地丰富了单像素成像的理论系统,提升了研究者对光学编码与广义逆问题的认识,可以说是一次光学与数学在成像领域的碰撞,这一碰撞正印证了计算光学成像的计算与光学两大重要组成部分,同时也将单像素成像由一个狭义的光学成像理论扩展到了一个广义的成像类别。

受限于单像素的探测机制,其成像过程往往需要大量的编码以提供足够的重建约束。因此,单像素成像的缺点也非常明显,其成像分辨率基本与编码次数成正比,在高分辨成像与高速成像场景下,单像素成像方案通常难以满足实际成像需求。正因为如此,有关单像素成像的应用探索一直集中于极弱光成像与特殊波段的成像,比如单光子成像[20]、红外波段成像[21,22]、太赫兹波段成像等[23,24]。在这些场景下,面阵相机的发展还不成熟,单像素的探测机制无疑具有非常大的成本优势。与此同时,通过提升成像维度降低单像素成像在测量时间上的弱势,是对单像素成像应用场景的另一种探索。光谱维度[25,26]、空间维度[27,28]、四维光场[29]、偏振维度[30]等融合多个测量维度的单像素成像方案被相继提出,有效丰富了单像素成像的应用场景。而作为对单像素成像维度的扩充,相位成像在最近几年同样得到了越来越多的关注。

受限于光电探测器的响应能力,传统的光学探测设备通常只能探测到光的强度变化,很难直接探测到光场的相位分布。而光的相位分布通常蕴含强度测量难以表征的物体信息,比如溶液浓度分布、表面深度分布、材料应力分布等。因此,相位信息的测量在光学成像领域具有举足轻重的地位,特别是在生物成像[31]、微纳测量[32]、材料表征[33]等领域具有非常大的应用需求。相位信息的测量最早可以追溯到上世纪初期,材料领域的研究者利用X射线衍射图样分析晶体材料的晶格结构,而狭义上的相位测量则要从Zernike相衬说起[34]。相衬成像利用频谱编码、照明编码、微分干涉等方式,将相位的变化转化到强度变化上来,从而帮助研究者看到传统成像器件无法直接探测的信息,在生物成像领域得到了非常广泛的应用。虽然相衬成像解决了“看不见”的问题,却不能解决“看得准”的问题,对相位分布的定量测绘是解决高精度测量问题非常重要的途径。随着数字光学的发展,计算全息技术的提出给相位信息的定量测量提出了解法。通过对干涉图样的数值再现即可同时重建复光场的振幅和相位分布。然而,干涉记录过程非常容易受到环境震动与噪声的影响,而且这种影响是波长量级的,对测量系统的稳定性有着较高的要求。为了提升记录的稳定性,衍射成像方案通过借助一定的先验条件,可以从衍射强度图中重建获得光场的复振幅分布。典型的衍射成像方案主要包括相干衍射成像(CDI)和强度传输方程(TIE)[35−37]。而得益于单像素成像在弱光成像、特殊波段成像等领域的优越性,单像素成像在复光场测量领域也具有一定的成像优势。目前复光场单像素成像大多数是把现有的成像方案与单像素成像联系起来,比如利用单像素成像测量相衬图、全息图、衍射图等方式,在引入单像素成像的同时基本保留了原有成像方案的缺点[32,38−40]。这其中最大的原因还是相位的分布变化不会明显改变光束的总体强度,因此传统的桶探测器不能探测相位的空间变化,仍旧需要通过测量干涉、衍射图的强度分布间接重建相位。为了测量光束的相位变化,一些学者将一个小孔置于传统桶探测器前,在频谱面测量某一频点的强度变化,复光场相位的变化可以引起光场的频谱分布变化,进而通过这种变化重建出复振幅分布[41,42]。这种方案直接将复光场分布编码到一维探测序列中,不借助任何的参考臂干涉、不采用任何先验条件及边界条件,具有极高的成像鲁棒性。

本文首先介绍单像素成像的基本原理与相位成像的主要工作原理,之后从相衬、干涉测量、衍射测量三个方面分别介绍单像素成像理论在复光场测量中的应用,并对现有方案的优缺点做重点讨论。

1 单像素成像与复光场测量

1.1单像素成像基本原理

单像素成像的理论本质是利用一系列的二维编码,将成像场景编码到一系列的一维探测序列中,其基本实验装置如图1所示[43]。在主动结构光照明情况下,经过结构光编码的光束被投影到物体上,物体反射的光被单像素探测器收集;在被动光源照明情况下,照明光被物体表面反射到空间光调制器上,随后经过调制后光束被单像素探测器收集。不断改变编码图样并进行同步探测获得一维探测序列,便可以通过探测值与预存的调制图样重构出物体的二维像。

图1 单像素成像原理图。(a)单像素成像的被动照明模式;(b)单像素成像的主动照明模式[43]Fig.1 Schematic diagram of single-pixel imaging.(a)Passive illumination mode for single-pixel imaging;(b)Active illumination mode for single-pixel imaging[43]

为了探究单像素成像的实际数学意义,将二维调制矩阵重新排列为一维行向量,并按照其调制顺序将多幅调制图样按行重组,获得一个二维测量矩阵,记为A,A∈RM×N,N为单幅调制图样的像素数,M为实验测量次数,即调制图样数量。同样,将成像场景二维分布变换为列矢量,记为x,x∈RN。探测器探测M次得到的探测值组成的一维列向量记为y,y∈RM。则探测过程可以表示为

而单像素成像的重建过程可以简单地认为是一个求解广义逆问题的过程,表示为

特别地,对于基于强度关联算法的单像素成像[44],其重建过程可以化简为

随着采样数目的增加,矩阵ATA的分布会在统计上逐步接近于IN,即N阶单位阵。换句话说,若想在单像素成像中获得清晰的重构结果,就要设法让ATA更趋近于单位阵,这也就解释了为什么当测量矩阵接近正交阵时重建质量要比传统随机矩阵好很多。而对于压缩感知重建[45],则可以看作在稀疏约束的情况下求解广义逆问题

此外,通过人工神经网络求解广义逆问题也是解决单像素重建问题的方法之一。但是由于需要大量的数据进行训练,而单像素成像的实际物理过程又比较明确,因此其在实际应用中往往不会被优先考虑。

在计算成像中,基于各种约束条件的广义逆运算求解在孔径编码成像、散射成像、相位恢复、解卷积、全息再现等方面得到了广泛的应用。特别是孔径编码、散射编码等成像方式,可以看作单像素成像在空间、时间、光谱等维度的复用成像,这也印证了单像素成像在应用上的潜在价值。

1.2复光场测量理论概述

传统探测器只能探测物体的强度信息,对弱吸收材料、反射物体等样品的特征变化难以捕捉,因此相位成像在生物成像与精密测量领域有着非常重要的作用。在光学上,对相位参数的成像主要分为相衬成像和定量相位成像。相衬成像是一种定性的成像方式,主要是通过一定的手段将相位变化转化为振幅分布,进而被传统强度探测器捕获,由于样品本身的强度分布会对相衬结果产生一定的影响,因此相衬成像更适用于透过率比较高的样品。而定量相位成像则不仅可以定量地重建光束的相位差异,还可以同时获取其振幅分布,实现对光场复振幅的测量,具有更高的普适性。通常,复光场的测量方案包括干涉法和衍射法,干涉法通常计算简单,但是由于干涉光路的引入,其测量过程对系统稳定性要求较高;而衍射法成像过程相对鲁棒,但是其重建过程往往需要借助一定的支撑条件,比较复杂。

1.2.1 相衬成像技术

相衬成像于1934年由Zernike提出[34,46],其通过在成像频谱面引入一个相移滤波的方式推迟样品直射光或衍射光的相位,实现了相位信息的增强,从而可以采用传统的相机或者人眼直接观察到物体的相位信息。但是,Zernike相衬有一些问题很难克服,比如光晕效应、孔径限制造成的空间分辨率不高等现象。Nomarski在1955年提出了差分干涉相衬方案(DIC)[47],其巧妙地利用沃拉斯顿棱镜,借助光的双折射效应将一束光分成两束,两束光通过物体时位置有一定的偏差。在成像面,让两束光再次利用双折射效应汇合发生干涉,其干涉图反映的便是物体的相位梯度信息。由于没有Zernike相衬滤波中的孔径限制,差分干涉能够充分利用成像系统的数值孔径,从而实现高分辨率成像。在此基础上,Hamilton和Sheppard[48]首次提出了差分相衬(DPC)的概念,而Metha和Sheppard则于2009年首次实现了全场的DPC[49],其利用非对称的部分相干光照明,将相位信息转换为不同照明下的强度变化信息,仅需两幅强度图像的微分运算即可获得相位梯度信息。值得说明的是,DPC系统的相位梯度与样品的实际相位关系是唯一映射的,这意味着DPC方案同样具有定量相位成像能力。

1.2.2 复光场干涉测量

随着数字光学的发展,计算全息技术的提出给复光场的定量探测提出了解法。全息技术最早由英国科学家Gabor于1948年提出[50,51],采用全息记录的方式,可以将物体真正的三维信息记录于一个全息干板上,其基本过程是利用干涉原理记录复光场并利用衍射原理再现波前。通过将全息干板换成CCD相机,便可以实现复光场的数字获取与波前重建[52],但是,同轴计算全息在数字波前重建的过程中会受到零级像和共轭像的影响,而离轴全息[53,54]虽然可以解决同轴全息中像叠加的问题,但是离轴的夹角会影响重构光场的空间精度,夹角越大重构图像的空间分辨越高,但对探测器的空间分辨率会有更高的要求。最近,Zhang等[55]基于目标光场的梯度先验,提出采用凸优化的方式去除同轴全息中的共轭项问题。这一方法为全息技术提出了另一种解法,但是考虑到重建中的先验问题,其仍旧会面临重建频谱精度的问题。进一步地,Yamaguch和Zhang[56]将相移干涉理论引入到计算全息。采用同轴相移全息的方式,既解决了共轭像问题,又将对探测空间分辨率的要求降到了最低,同轴相移全息已经被广泛应用于三维成像、精密测量等领域。

1.2.3 复光场衍射重建

干涉系统最大的问题在于对干涉光路稳定性的要求,能否在不借助干涉参考光的情况下利用衍射现象重建光束的复光场,是研究人员一直试图解决的问题。相干衍射成像理论通过借助一定的先验条件[35],省略了参考光路,极大地增强了探测过程的稳定性。通过拍摄复光场傅里叶平面的强度信息,借助物面的振幅约束,采用一定的相位恢复算法便可以通过迭代收敛得到光场的相位信息[57−59]。这种方法虽然可以从衍射强度图中重建复光场信息,但是其重建鲁棒性往往不高,一方面重建需要一定的约束条件,另一方面其收敛过程有一定的概率收敛不到正常的重构结果。为了增强其收敛过程的稳定性,Zhang和Rodenburg[60]将一个相位编码板引入到CDI成像过程中,引入了一个额外的编码约束,从而增强了其收敛的稳定性。此外,为了解决先验信息缺失下的光场重构问题,叠层成像被借鉴到复光场重构中来,其主要的成像方式分为叠层迭代引擎成像(PIE)与傅里叶叠层成像(FPI)[61−63]。PIE成像借助移动的照明光源对物体进行迭代照明与投影计算,有效增强了迭代收敛的稳定性,同时也提升了成像的区域大小。FPI则借助不同入射角度的照明,采用类似的交替投影方式进行复光场重构,其不仅可以增强收敛稳定性,还可以扩大原有系统的孔径限制,实现超分辨成像。另外,区别于迭代相位恢复算法,TIE也被用来由衍射图样求解复光场的分布。通过测量待求平面上的光强分布以及光强轴向微分,TIE可以直接通过数值求解重建复振幅分布,相比于迭代恢复,具有更低的计算要求。但是,如同迭代相位恢复中的约束问题一样,TIE的求解也面临一些边界条件问题,在强吸收、大尺寸情况下也面临着挑战[64]。

2 基于单像素成像理论的相衬成像

光场的相位分布通常可以反映光穿过物体的厚度、材质、深度等信息,在三维测量、生物成像等领域具有极高的测量价值,但却难以被传统强度探测器直接感知。因此,将不可感知的相位信息转化到可感知的强度、偏振等光学参量上是实现相位感知的有效途径。光场相位虽然不容易被感知,但却对光场的传播起着非常重要的作用。因此,如果在光传播的过程中定制化地改变其相位分布,则可以将相位变化信息转化到强度信息中去。而Zernike相衬技术就是基于这一原理实现的,通过在频谱面放置相位滤波器,使零级衍射光的相位相对其他频次的相位改变±π/2,使低频区域的光和高频区域的光在像面发生干涉,即可将光场的相位信息定性地转化到强度分布上来。相似的方法还有螺旋相衬成像[65],通过在频谱面放置径向希尔伯特变换滤波器,使光束携带一个螺旋型相位。可以近似理解为该滤波器为一个沿角度方向的微分滤波器,实现沿角度方向的微分滤波可以在像面得到各个方向的相位梯度信息,从而实现相位的边缘探测。

受这类方法的启发,单像素相衬成像应运而生,旨在为极限探测条件下的相位测量提供解决方案。2011年,Shirai等[66]结合传统频谱滤波相衬成像和单像素成像,提出了一种经典非相干光单像素相衬成像方案,其原理图如图2所示。该方案中,在传统无透镜单像素成像的参考臂上放置了一个相位滤波器,光场经过滤波并传输一段距离后,由一单像素探测器在探测面做面阵扫描成像;另一方面,在信号臂放置物体和透镜,经过它们的光场被另一单像素探测器收集做固定探测。其中光源到扫描探测器的传播距离与光源到物体的传播距离相等(zc=za+zb),滤波器到扫描探测器的距离和物体到固定探测器的距离满足透镜的成像关系。根据衍射积分方程可以推导出该方案关联运算得出的结果与4f相干成像系统得到的强度表达式相同,因而该系统可以等效为一个4f相干成像系统实现相衬成像。类似地,Liu等[38]借助定制结构光编码实现了无参考臂的单像素螺旋相衬成像,实验装置如图3所示,其借助空间超像素技术,利用DMD产生不同方向的平面波实现频谱扫描,同时将涡旋相位的空间结构同步投影到物体上。设物体为O(x,y),不同方向的平面波复振幅为U(x,y,kx,ky)=exp[−j(kxx+kyy)],涡旋相位板为H(kx,ky),其中(x,y)为空间坐标,(kx,ky)为频谱坐标,那么物体经过平面波扫描和结构光调制后的频谱分布为

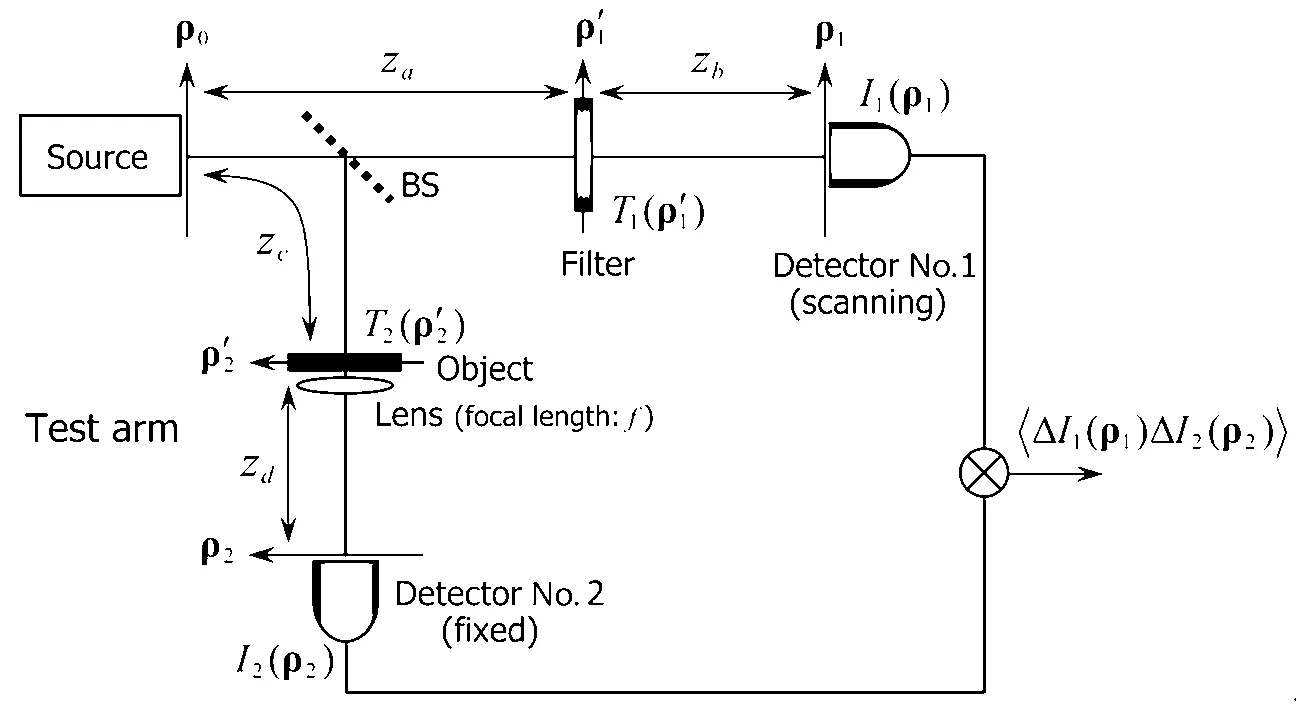
图2 单像素频谱滤波相衬成像实验装置图[66]Fig.2 Experimental setup of single-pixel phase contrast imaging based on the frequency-domain filter[66]

图3 单像素螺旋相衬成像实验装置图[38]Fig.3 Experimental setup of single-pixel spiral phase contrast imaging[38]

由(5)式可见,物体受到调制的效果可以等效为在物体的频谱面放置螺旋相位板。实验通过四步相移探测计算得到物体振幅或相位的边缘信息的频谱分布,再由傅里叶反变换恢复出强度信息,其本质与在4f系统频谱面放置滤波器的相衬成像方式是一样的。该实验将螺旋相位板加载到了单像素探测器的多步傅里叶频谱采样中,因此相较传统螺旋相衬成像具有更高的探测效率,并且可以应用在特殊波段的相衬成像中。但单像素成像是以时间成本换取空间信息的技术,该成像过程采用频谱扫描和四步相移再次增加了采样数据量和时间成本。

另一类相衬成像方式不是利用傅里叶变换的频谱滤波,而是将参考路的相位滤波器和信号路的相位物体放在光源的像平面,对物体进行逐点扫描,通过关联运算依次恢复扫描区域的相位梯度信息,最终恢复出物体的边缘增强图像。2009年,Jack等[67]基于量子关联成像实现了相衬成像,由BBO晶体发生I型非共线参量下转换产生纠缠光子对,一路光作为闲频光成像在相位滤波器上,由一个点探测器收集反射信号,其中相位滤波器的实现方式是用SLM加载不同拓扑荷数轨道角动量的全息图或不同拓扑荷数轨道角动量组合的全息图;另一路作为信号光成像在相位物体上,物体逐点移动。通过两路信号的符合测量,可以逐点恢复出物体的相位梯度信息。该实验一方面发挥了量子成像非局域的优势,另一方面突破了频谱面限制,实现了在像面滤波恢复相衬图像,但纠缠光源存在光子对产生效率低等缺点。对此,Song等[68]基于赝热光照明实现了螺旋相衬关联成像,实验装置如图4所示。激光通过一个旋转毛玻璃(RG)产生的散斑被分束器分为两路,分别成像在相位物体和SLM上,通过局部二阶关联逐点恢复出物体相位的边缘增强图像。利用光场的二阶相干性,即使采用非相干的赝热光,也可以实现对物体相位的信息提取,而不受传统成像特定情况下光源的相干性限制。此外,用赝热光源代替纠缠光源克服了光子产生效率低、成本高等问题,同时又保留了非定域成像的优势。然而,这两种方案均是通过移动物体进行逐点扫描,逐点恢复相位物体的边缘信息。一次只对物体的局部进行探测不可避免地增加了时间成本,物体的分辨率也受到采样次数的制约。同时,采样过程中需要物体不断移动也给实际应用带来一定限制。

图4 相位物体的热光边缘增强鬼成像实验原理图[68]Fig.4 Setup schematic of the thermal light edge enhancement ghost imaging of phase objects[68]

基于关联成像或单像素成像理论的相衬成像突破了傅里叶频谱面放置滤波器的限制,实现了非定域相衬成像,并且可以设计不同的空间结构光来实现针对不同需求的相衬成像,在无先验成像的情况下直接得到相位物体的边缘信息,应用至边缘检测等领域。但目前单像素相衬成像还是一种定性观察相位的方式,其恢复出的强度与物体的相位不呈线性关系,不能对相位进行定量求解,故而可能无法客观准确地反映物体的实际相位信息。

3 基于单像素成像理论的干涉编码复光场测量

数字全息是相位成像的一种有效方式,对于单像素复光场成像来说是一个很好的借鉴方案。相较于单帧全息技术,相移数字全息具有同轴设置、重建分辨率高、无共轭像等优势,更适用于成像分辨有限的单像素成像方案。Clemente等[69]率先将相移数字全息技术与单像素成像技术相结合,利用传统的Mach-Zehnder干涉仪,借助三步相移技术实现了复透过率物体的测量,其基本成像结构如图5所示。由激光器发出的相干光被分束器分成物光和参考光两路。在物光这一路,类似于传统的单像素成像系统,利用液晶空间光调制器对样品进行编码;而在参考光这一路,则通过一个相移器实现三步相移操作。每次相移后,干涉图的强度被单像素探测器采集。通过三步相移技术,可以从单像素的强度探测中求得其相位信息,进而借助单像素成像理论实现对复光场编码的求逆运算,重建出物体的复振幅透过率。2017年,Martínez-Le´on等[70]利用迈克尔逊干涉仪再次证明了单像素相移全息成像方案,同时用DMD替换原有方案中的SLM,提升了测量速度,其光学实现原理如图6所示。

图5 基于Mach-Zehnder干涉仪的相移数字全息单像素复场成像结构图[69]Fig.5 Experimental setup of single-pixel complex field imaging structure of phase shifted digital holography based on Mach-Zehnder interferometer[69]

图6 基于迈氏干涉仪的相移数字全息单像素复场成像结构图[70]Fig.6 Experimental setup of single-pixel complex field imaging structure of phase shifted digital holography based on Michelson interferometer[70]

然而,无论是利用Mach-Zehnder干涉光路还是利用迈氏干涉光路进行干涉强度测量,额外的参考光路都会导致系统易受环境震动影响,从而影响成像鲁棒性。为了解决这一问题,Ota和Hayasaki[71]、Liu等[72]相继提出一种共轴的单像素复场成像方案。在Ota和Hayasaki[71]的方案中,空间光调制器的中心区域用于实现相位结构光编码,而结构光边缘区域则作为参考光,产生相移干涉,其实现原理如图7所示。将复振幅结构光编码重新排列为一维行向量,将第m张结构光编码记为wm=[wm1,wm2,···,wmN]T。按照调制顺序,将多幅结构光按行重组获得一个复振幅二维测量矩阵,记为W=[w1,w2,···,wM]。成像物体记为u=[u1,u2,···,uN],其中un=anexp(−iφn),an为物体第n点的振幅值,φn为物体第n点的相位值。通过参考光路的相移测量,可以求得第m次探测的复值信号νm,表示为

图7 单一光路相移干涉示意图[71]Fig.7 Schematic of single optical path phase shift interference[71]

经过m次采样后,输出信号组成的向量可以记为ν=[ν1,ν2,···,νM]。总探测过程可以表示为ν=Wu,则物体的复振幅重建为u=W−1ν。而在Liu等[72]的方案中,DMD被以棋盘格的形式划分为彼此间隔的区域,如图8所示,一部分用来实现结构光编码,而另一部分则作为参考光。此外,也有学者提出利用空间光调制器的直接反射量作为参考光[73],通过在相位编码中引入相移实现相移干涉,这一方案相较于前述两种方案具有更好的编码利用率。此外,以上三种方案均在文中进一步明确了单像素桶探测器放置于干涉光场的频谱面,且在探测前放置一针孔片,限制实际的探测区域,实现单点测量。这一改进相较于Clemente等[69]的方案更契合理论过程,有效提升了成像质量。值得注意的是,即使前述几种单像素干涉测量方案采用了不同的干涉测量装置,但都采用了基于Hadamard矩阵的相位编码方案,也正得益于Hadamard矩阵的正交特性,上述方案可以在理论上实现完美重建,且采样倍率与相移步数相同。也就是说,在四步相移方案中,400%的采样率即可重建物体的复振幅透过率分布。

图8 (a)单像素复场成像的实验装置图;(b)点探测器示意图;(c)调制掩模组成图[72]Fig.8(a)Schematic of the experimental setup for the complex wavefront reconstruction using the single-pixel imaging technique;(b)Schematic of point detector;(c)Illustration for how to construct the patterns[72]

除Hadamard编码外,傅里叶编码单像素成像是另一种典型的正交基成像方案,其利用不同方向、不同角度的相移正弦条纹记录目标物体的频谱分布,相较于Hadamard编码具有更直观的物理意义,已经在实空间成像领域得到了非常广泛的关注。而在复光场成像领域,利用相移和频谱扫描技术同样可以通过一个单点探测器遍历复光场的频谱分布,进而通过反傅里叶变换获得复光场分布,其基本成像光路如图9所示[74]。作者将DMD调制面以棋盘格的方式进行分区,分别进行二值光栅编码与参考光相移编码,实现了同轴相移干涉。通过傅里叶基编码的方式,复光场成像由原来的复数矩阵的求逆问题转化为求逆傅里叶变换的过程,同时借助自然物体的频谱低频集中的先验条件,有效降低了高分辨成像的重建时间。此外,借助DMD的超快调制技术,该方案还实现了动态的复光场成像,成像物体是一个旋转的拓扑荷数为3的涡旋光束,实验结果如图10所示。

图9 傅里叶单像素复光场重构实验结构图[74]Fig.9 Schematic diagram of Fourier single-pixel complex amplitude optical field reconstruction experiment[74]

图10 实时动态复场恢复图,上图为重构振幅,下图为重构相位[74]Fig.10 Schematic diagram of real time dynamic complex field reconstruction.The first row is the reconstructed amplitude,and the second row is the reconstructed phase[74]

基于干涉的单像素复光场成像方案借助相移技术,将实空间单像素成像中的逆运算扩展到了复数域。在成像过程中,相位编码技术构建了复编码矩阵,而相移技术则辅助从强度探测获得探测点的复振幅信息,进而通过复数域的逆运算重建复光场信息,因此,其基本原理与实空间单像素成像仍然是相同的。但相移探测的引入也进一步限制了单像素采样与实际重建分辨的关系,加长了单像素成像的采样时间,未来可以进一步结合复光场稀疏优化做进一步探索。

4 基于单像素成像理论的衍射编码复光场测量

衍射成像通过光束传播过程的强度分布变化从衍射图样中重建光场的复振幅分布,在复杂环境下,其相较于干涉成像具有更好的成像鲁棒性。然而传统单像素成像通常仅探测光束的总体光强变化,不能感知光束的强度分布变化或者相位变化,而波前的相位变化往往不会改变光束的总体强度,因此难以直接应用到相位测量中。为了从单像素强度探测中重建复光场信息,一种比较直接的方式是直接由单像素成像代替传统衍射成像中的面阵相机测量衍射面的强度分布,再从衍射面强度分布结合相位恢复算法而重建复光场。但是,由于单像素成像的探测分辨通常与探测次数和编码分辨成正比,而现有技术很难实现高分辨、超快速的动态编码,使得单像素成像分辨率受限。考虑到相位恢复中对探测面采样率的要求,这种方案在成像精度与重建稳定度上都面临难以避免的问题,因此在衍射成像中鲜有报道[75]。

为了解决这个问题,Horisaki等[76]融合了压缩感知重建与相位恢复过程,并且将单像素成像中的桶探测器换成了点探测器,其成像过程如图11(a)所示。单点探测器的引入使相位信息与编码信息直接建立联系,编码信息为重建过程提供了额外的参考约束,提升了重建鲁棒性。为了从强度探测重建复光场信息,Fienup[57]借助GS(Gerchberg-Saxton)相位恢复算法从强度探测序列中重建探测面的复光场信息,再借助压缩感知理论,结合编码过程从欠定采样中重建物体复光场分布。从重建角度来讲,上述迭代过程仍旧是两个分离的过程,而且为了保证正常收敛,其在重建过程中加入了全变分约束,也使得重建质量细节模糊,其重建结果如图11(b)、(c)所示。随后,Horisaki等[40]进一步改进了原有的成像过程,将结构编码探测改为结构光照明,这在生物成像中可有效降低光强对生物组织的损伤,从而提升系统的光强利用率,成像光路如图11(e)所示。在重构方面,Bioucas-Dias和Figueiredo[77]将原来相对分离的重建过程进一步整合,提出了基于TwIST算法的交替投影相位恢复算法。具体重建过程整体与传统GS相位恢复算法一致,不同的是将其交替过程中的反向传播过程用TwIST算法代替,正向传输过程保持不变。这一改进有效融合了压缩感知与交替投影相位恢复的基本结构,充分利用了编码结构的约束,在一定程度上提升了相位的重建质量,其重建结果如图11(f)、(g)所示,可以看出,成像质量相较于前述方案具有非常明显的提升。

图11 单像素压缩衍射成像原理图。(a)结构编码探测原理图;(b)重建振幅结果;(c)重建相位结果;(d)显微成像参考结果;(e)结构编码照明原理图;(f)重建振幅结果;(g)重建相位结果;(h)显微成像参考结果[40,76]Fig.11 Schematic diagram of single-pixel compressive diffractive imaging.(a)Schematic diagram for structured detection scheme;(b)The retrieved amplitude result;(c)The retrieved phase result;(d)Reference image captured by amicroscope;(e)Schematic diagram for structured illumination;(f)The retrieved amplitude result;(g)The retrieved phase result;(h)Reference image captured by amicroscope[40,76]

受点探测的单像素成像模式启发,Li等[42]提出了基于纯相位编码的单像素复光场探测方案,基本成像光路如图12所示。在实验结构中,相位编码直接被一中继系统投影到待测物体平面,有效避免了由衍射距离估计带来的计算误差。借助于桶探测器前的小孔,桶探测器只用于检测傅里叶频谱中零阶频的强度,而不是像传统单像素相机那样去搜集光束的总光强,因此,即使实验采用直接的纯相位编码,单像素探测器仍然可以感知波前的变化。在探测器所在傅里叶平面的光场分布可以表示为

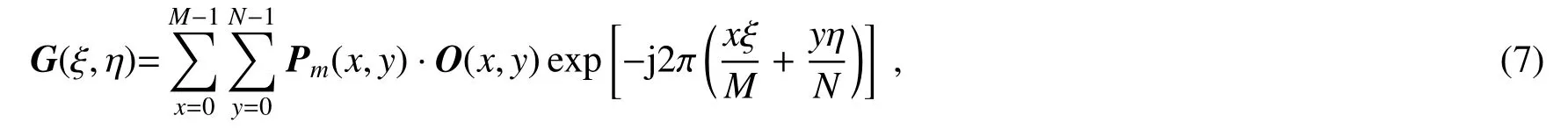
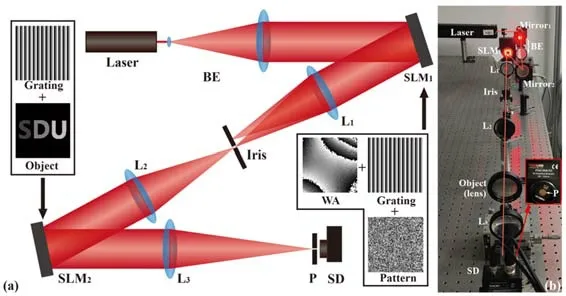
图12 基于相位编码的单像素衍射成像原理及实验装置图[42]Fig.12 Schematic diagram and experimental setup of single-pixel diffractive imaging based on phase-only modulations[42]

式中:Pm(x,y)为第m张结构光矩阵,O(x,y)为物体的复振幅分布。单像素探测器只用于收集零阶频的强度,因此探测器探测得到的信号为

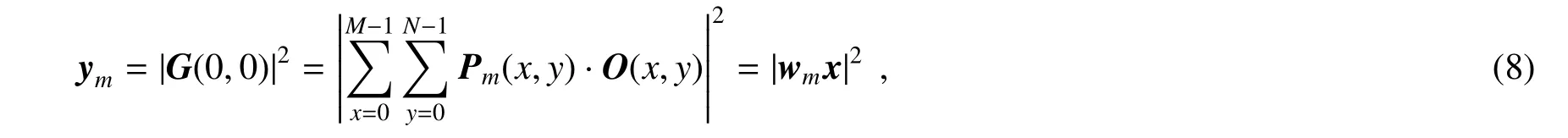
式中:wm为第m张结构光矩阵的一维变形,x为物体的一维变形。在实验设置中,探测点的位置是固定的,与待测物体的分布无关,恒定为物体后傅里叶透镜的后焦点位置,可以非常方便地通过一束平行光确定该点的位置。为了获得更好的探测信噪比,该方案依据探测点的零频属性,针对性地通过编码矩阵设计,在保证充足波前编码约束的情况下充分增强了探测点的光强值,有效提升了探测信噪比和光强利用率。此外,采用相位编码也有助于对成像系统本身的相差进行波前矫正。通过在编码的同时加入额外的矫正波前,可以实时地对系统的波前误差进行矫正,有效避免了背景波前突变对成像振幅分布的影响。在重建方面,采用了基于非凸优化的TAF(Truncated amplitude flow)算法[77],相较于传统的交替投影法,TAF算法具有更稳定的收敛特性,同时又具有比大多数凸优化算法更快的收敛速度。实验结果表明,在理想条件下采用300%的采样率即可接近完美地重建复光场信息。此外,即使在复杂实验噪声下,也可以在300%采样率下获得相当的成像质量,其具体成像结果如图13所示。

图13 不同采样率下的复光场成像(a)仿真和(b)实验结果[42]Fig.13 Reconstructions of a complex object with different sampling ratios.Both(a)simulation and(b)experimental results are presented[42]

采用相位编码的缺点也是显而易见的,目前基于液晶双折射效应的空间光调制技术难以实现低成本、高速度的相位调制,而单像素成像技术本质上又是利用时间编码换取空间分布,需要大量的编码探测。因此,采用相位编码无疑限制了该方案的成像速度。为了提升单像素复光场成像的成像速度,北京理工大学课题组采用强度编码的方式,在远场实现了复光场的单像素测量,成像过程如图14所示[41]。振幅照明编码被直接投射到复振幅物体上,一个单点探测器置于远场探测平面,用来探测傅里叶零频点的强度变化。通过远场测量,该成像方案在探测端实现了无透镜成像,有效提升了探测的纵向自由度。借助于超高速DMD,其在0.7 s左右即可实现64 pixel×64 pixel分辨的单像素复光场探测,这一编码速度是传统液晶空间光调制器的数百倍,有效降低了成像时间。但是,强度编码并不能为复光场测量提供足够的约束,从探测角度讲,强度编码后的复光场与其复共轭具有相同的探测序列。因此,在强度编码下,相位恢复过程至少有两个最优解,未来仍旧需要借助其他先验条件对收敛过程进行适当约束。此外,由于成像系统中可能存在一些固有的相差,会对成像波前产生一定的影响。而采用直接的振幅编码难以从编码过程中矫正这些相差,通常只能后期从重建相位中减去背景相位,以实现相位矫正,其相位矫正过程与重建结果如图15所示。但是,如果背景相位上存在某些固有的相位突变或涡旋,则不可避免地影响重建振幅的分布,这一点还需要在今后的工作中做进一步地研究。

图14 基于振幅编码的无透镜单像素衍射成像原理[41]Fig.14 Schematic diagram of single-pixel diffractive imaging based on phase-only modulations[41]

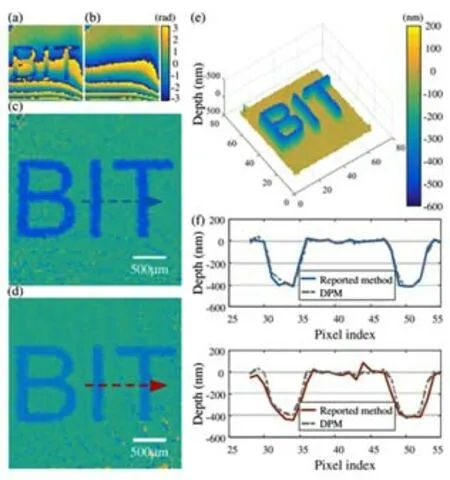
图15 可见光(488 nm)和近红外光(980 nm)照明下,透明相位物体的定量相位成像结果。(a)未修正的结果;(b)背景相位分布;(c)可见光下的校正结果;(d)近红外光下的校正结果;(e)物体的三维分布;(f)沿高亮线的深度剖面图[41]Fig.15 Quantitative phase imaging results of a transparent phase object using visible light(488 nm)and near-infrared light(980 nm).(a)Uncorrected result;(b)Background phase distribution;(c)Corrected result under visible light;(d)Corrected result under near-infrared light;(e)3D distribution of the object;(f)Depth profiles along the highlighted lines[41]

总的来说,基于衍射的单像素复光场探测在一定程度上解决了传统干涉测量对稳定性的要求,但是仍然面临采样速度、成像分辨等问题,需要进一步解决。此外,利用孔径限制探测区域,在频谱空间实现单点测量是大多数研究者采用的测量方案,而频谱空间的采样孔径大小与物空间像的重建精度无疑具有密切的联系,这一关系同样有待进一步论证。这一系列问题制约着单像素衍射成像技术的发展,也同样促进着其逐渐走向成熟。

5 总结和展望

从单纯的相衬成像到复光场的定量成像、从干涉成像到衍射成像,单像素复光场成像的出现与发展为特殊场景下复光场成像打开了新的大门。通过连续的时间编码,单像素复光场成像将复振幅信息编码到单像素探测序列中,不仅降低了成像系统的探测要求,也为相位信息的重建提供了一定的重建约束,提升了相位重建的稳定性。本综述从单像素成像与复光场成像的基本原理出发,分别介绍了基于单像素成像的相衬成像、干涉成像和衍射成像的研究现状与最新进展。这些工作不仅完善了单像素成像的理论体系,也扩展了复光场成像在弱光条件、特殊波段等领域的应用场景。然而,成像分辨与成像速度问题一直是制约单像素成像发展的两大问题,这两个问题同样存在于单像素复光场成像中,因此目前已有的研究工作仍大多处于理论研究层面,相较于现有的面阵成像方案,并未表现出充分的成像优势。如何在解决成像分辨与成像速度的同时保留成像过程中的探测优势,将会是单像素复光场成像走向实际应用必须要解决的重大挑战。相信随着信息技术与微机电技术的发展,这两个问题将会逐渐得到解决,单像素复光场成像也会由理论研究走到实际应用中来。