电子倍增器脉冲信号图形化离线分析软件

彭华兴，闫保军，刘术林,3，张斌婷，韦雯露

（1. 中国科学院高能物理研究所 核探测与核电子学国家重点实验室，北京 100049；2. 中国科学院大学 物理科学学院，北京 100049；3. 中国科学院大学 核科学与技术学院，北京 100049）

引言

电子倍增器（electron multiplier，EM）是一种真空电子元件，主要包括3 种类型：单通道电子倍增器、打拿极电子倍增器和微通道板，其工作原理是基于材料的二次电子发射特性，以及电子在加速电场作用下，不断碰撞材料表面，实现雪崩的倍增过程。EM 可以做成开放式结构，即将EM 安装在真空法兰上，拆卸和更换方便；也可以做成密封式结构，即将EM 放置在真空管壳内，外部不用再提供真空环境，使用简单。这2 种结构（结合转换材料）均可以实现对入射粒子（如电子、光子、离子等）的有效探测，在微光像增强器[1-3]、真空紫外谱仪[4-5]和质谱仪[6-7]中具有广泛的应用。

根据入射粒子流的大小，EM 可以在模拟和脉冲2 种状态下工作。以微通道板为例，当入射电流为280 fA 以上时（对应的计数率高于1.75 MHz），EM 主要工作在模拟状态，其性能参数包括增益、暗电流、体电阻等，通过测试输入电流和输出电流的大小，可计算出电子倍增器的增益，一般电子倍增器生产厂家均提供该指标测试结果。当入射电流小于280 fA 时（对应的计数率小于1.75 MHz），电子倍增器主要工作在脉冲状态[8]，在阳极上感应出离散的脉冲信号，其性能参数包括增益、分辨率、后脉冲率、脉冲波形前沿时间分布等。目前，直接对EM 脉冲性能开展研究的工作比较少，少数EM 生产厂家仅给出脉冲状态下的增益和分辨率测试数据，而其他参数并未给出，对于某些应用领域（如高能物理探测实验），需要准确获得这些参数时，往往要求用户自行搭建测试系统进行测量[9]。通常采用2 种方法测试EM 的脉冲性能参数，第1 种是采用商用的电子学插件和配套分析软件[10-11]，对阳极输出的脉冲信号进行大统计量的测试，包括脉冲信号的幅度谱测试、电荷量测试和时间性能测试，该方法比较常用，但由于电子学系统采样率和存储深度有限，无法准确测试较宽时间范围内的后脉冲情况；第2 种方法是利用高性能示波器对阳极输出的大量脉冲波形进行测试并记录，然后进行离线分析，结合自行开发的数据分析软件，最终获得各种参数[12]。以测试前沿为2 ns 的脉冲信号为例，示波器采样率要求高于2.5 GHz，带宽高于175 MHz，若后脉冲出现在100 μs 的时间范围内，那么单个脉冲波形的测试点数为250 K，为了提高测试精度，通常需要测试1 万个以上的脉冲信号，然后进行离线分析。常用的数据分析软件，如Origin，无法满足离线分析的要求，一般采用可编程的程序实现对大统计量数据的分析，如采用ROOT 软件，优点是功能强大且是开源软件，其缺点是对数据分析人员的编程能力要求较高。为了便于数据分析及时获得EM 脉冲状态下的各种性能参数，基于图形化界面的离线分析软件获得了广泛关注，Labview 软件是最常用的编译平台之一，在数据分析处理方面Labview 经常需要使用C++、Python、Matlab 等其他语言进行混合编译来完成复杂的分析任务[13]。同Labview 相比，Python优势在于具有丰富的第三方库，从科学计算到图形化界面，涵盖各个领域，基于Python 进行离线数据分析具有操作简单、界面友好等特点。此外由于其是开源软件，因此使用免费，自由度高。另外和几GB 大小的商用软件相比，本文开发的软件体积小巧，不过百MB。为了及时获取EM 脉冲状态下的性能参数，减轻科研人员对相关数据分析的工作量，本文基于Python 开发了一套多模块集成的图形化分析软件，其核心数据分析部分采用Numpy、Scipy 等科学计算库进行编写，使用PyQt 将核心代码包装成为一个交互友好的可视化数据分析系统。

1 系统构成及算法介绍

该软件主要包含5 大模块，分别是波形分析模块、电荷积分谱分析模块、后脉冲分析模块、电荷数字转换插件（QDC）分析模块和前沿时间分析模块。图1（a）为软件的主界面，图1（b）为其中一个分析模块的界面。

图1 程序界面截图Fig. 1 Screenshot of program interface

各个模块的程序流程图如图2 所示。其中QDC 分析模块和电荷积分谱分析模块仅加载的数据类型不同，其他功能都相同，因此QDC 分析模块未在图2 中标出。

图2 程序流程图Fig. 2 Flow chart of program

1.1 波形分析模块及其算法

示波器采集并记录下阳极输出的大量脉冲信号，将这些包含信号幅度-时间的脉冲数据批量导入波形分析模块中可以获取脉冲信号的电荷积分谱，典型的脉冲信号波形及积分区间选取示意图如图3 所示，其中信号后沿出现振荡现象，和阳极结构以及测试电路的阻抗设计有关。

在指定的时间窗口内进行积分，时间窗口开始和结束时间分别为tw1、tw2，电压数值为U，求出积分值S0：

由于噪声和干扰的存在，实际测量过程中示波器的基线往往不在0 V 位置，经过测量发现示波器的基线符合高斯分布, 为了扣除基线晃动，需要在信号临近区域（见图3 中tp1到tp2）计算基线的平均值Up：

图3 脉冲信号波形及积分区间选取Fig. 3 Diagram of pulse signal waveform and integration interval selection

通过上述公式可以计算出一个脉冲波形信号的积分值，单位是伏秒（V·s）。若要得到以库仑为单位的电荷积分数值，需要将S1除以阻抗，鉴于不同设备阻抗有差异，因此软件中并没有计算出真实的电荷积分值，本文后续所有关于电荷积分的描述均默认指的是电压对时间积分得到的数值，这并不影响脉冲参数的分析。将大量脉冲波形信号进行积分后填入到合适的直方图中便可以得到电荷积分谱，如图4 所示。

1.2 波形分析模块及其算法

为了从图4 所示的电荷积分谱中获得脉冲状态下的性能参数，需要对谱图进行拟合分析，拟合结果如图5 所示，其中包含了5 个光电子峰。

图4 电荷积分谱Fig. 4 Charge integral spectrum

图5 电荷积分谱及其拟合分析Fig. 5 Charge integral spectrum and fitting analysis

电荷积分谱分析模块中采用了2 种模型：第1 种是高斯函数模型，可以对一些类高斯峰进行局部拟合：

1.3 后脉冲分析模块及其算法

通常在主脉冲信号后面一定时间范围内（约20 μs）会出现其他脉冲信号，即后脉冲，是EM 的主要背景噪声之一。后脉冲主要分为2 大类，第1 类是主脉冲后数ns 至数十ns 出现的快后脉冲；第2 类则是在主脉冲后μs 量级范围内出现的慢后脉冲。快后脉冲是由第一倍增级反射的电子到达光电阴极附近时又返回去经过电子倍增后产生的信号。慢后脉冲则是电子在倍增过程中碰撞残余气体使其电离，产生的正离子在电场作用下碰撞激发出额外的电子，这些电子再次经历电子倍增过程后产生脉冲信号，即离子反馈现象[16]。对于设计新型EM 结构抑制离子反馈现象，如研制弯曲通道结构的微通道板，需要详细测量后脉冲率；对于需要测量稀有事例的实验，比如寻找暗物质或者探测低能中微子，后脉冲信号成为一个不可忽略的因素[17]；因此研究后脉冲的特性对于EM 以及以EM 为核心的探测器件性能改进是十分重要的[11]。

图6（a）为典型的后脉冲信号波形，其出现时间比主脉冲延迟约3 μs；图6（b）和图6（c）分别为主脉冲和后脉冲放大图，后脉冲的寻找大致可以分为3 个步骤：1） 通过设定一个电压阈值来初步筛选后脉冲信号，该阈值可以在软件中自行设定；2） 寻找信号的峰值时间作为后脉冲的发生时间tp；3） 在软件中设定后脉冲信号的积分窗口Δtap，则后脉冲的积分区域为tp−∆tap/2至tp+∆tap/2，积分需要扣除信号基线数值，最终得到后脉冲信号的电荷积分Qap。

图6 后脉冲测试及分析Fig. 6 Post-pulse test and analysis

1.4 前沿时间分析模块及其算法

脉冲信号的时间特性包含前沿时间、后沿时间、渡越时间和渡越时间分散等。前沿时间分析模块主要对信号的前沿时间做分析处理，前沿时间定义为信号幅度的10%～90%所经历的时间，通过对信号前沿的散点进行拟合计算出前沿时间，如图7（a）所示。

图7 前沿时间分析及拟合优度Fig. 7 Leading-edge time analysis and goodness of fitting

前沿使用的拟合函数可以选择直线拟合或者三次函数拟合。在实际测量过程中并非所有信号都是标准的单电子信号，往往会出现多电子信号的堆叠以及畸变导致拟合效果较差。通过拟合优度R2来表征拟合的好坏，其取值范围在0～1 之间，越接近1 说明拟合效果越好，反之拟合效果越差。

2 测试系统

为了测试并验证图形化分析软件对脉冲信号数据分析的准确性，测试了打拿极光电倍增管（型号CR160）在脉冲状态下的性能参数，测试装置如图8 所示。采用同步触发的方法，信号发生器通道1 驱动LED 光源，通道2 作为触发门信号，2 路信号同频，调节一路信号的延迟，使得大部分光电子信号均出现在门信号窗口内，调节高压电源的电压数值，便可以得到不同电压下的光电子信号。分别使用力科示波器（型号HDO9204，带宽2 GHz，最大采样频率40 GS/s）和商用的QDC 电子学插件（型号CAEN V965A，小量程范围下刻度每通道电荷量为31.33 fC）对阳极输出的脉冲信号进行电荷积分，对2 种方法测试的增益和分辨率进行了比较；另外，分析了示波器采集波形的后脉冲和前沿时间分布等参数。

图8 测试装置Fig. 8 Physical drawing and schematic diagram of testing device

3 结果和讨论

3.1 脉冲状态下的增益和分辨率测试结果

选取PMT 的工作电压范围为1 250 V～1 550 V，间隔50 V 进行测量。调节信号发生器通道1 和通道2 的参数，见表1，使得PMT 工作在脉冲状态。在每个工作电压下，分别利用示波器和QDC 插件进行测量，示波器采集并保存2 万个脉冲波形，QDC 采集约75 000 个数据点。

表1 信号发生器通道1 和通道2 的参数Table 1 Parameters for signal generator channel 1 and channel 2

对于QDC 测量结果，利用软件读取QDC 测量的数据，按照公式（5）对电荷积分谱进行拟合，得到q1，σ1，µ。根据刻度过的QDC 每个通道的电荷量，计算出qreal=q1×31.33×10−15，测量结果见表3。

表3 QDC 测量结果Table 3 Measurement results of QDC

将表2 和表3 中的增益和分辨率分别绘制成曲线，图9（a）为2 种测量条件下的增益结果。不同工作电压下，利用示波器和QDC 分别测试增益结果的平均相对误差为2.8%；图9（b）为2 种测量条件下的分辨率结果，不同工作电压下，利用示波器和QDC 分别测试分辨率结果的平均相对误差为10.5%。2 种测量方式产生的误差一方面和统计误差有关，另一方面和QDC 与示波器内部电子电路的差异及其测量精度造成的系统误差有关。另外，测试过程中信号线在示波器和QDC 之间频繁切换，脉冲信号的形状受到外界干扰也会对测试结果造成一定的影响。

图9 示波器和QDC 分别测量PMT 结果对比Fig. 9 Comparison of measurement results for PMT by oscilloscope and QDC

3.2 后脉冲与前沿时间分布测试结果

选取PMT 工作电压为1300 V，调节LED 驱动电压为3.396 V，脉冲宽度为50 ns，使得PMT 工作在较强入射光照射状态下，利用示波器采集5000个脉冲波形，通过拟合此时的主脉冲光强期望为49.9 个光子。对所采集波形的后脉冲进行分析并绘制出散点图，见图10，横坐标为后脉冲出现的时间，纵坐标是后脉冲信号的电荷量。从散点图的分布中可以看到对于CR160 这种小型的光电倍增管的后脉冲主要分布在10 μs 以内，对于10 μs 以后的区域后脉冲的分布并无明显特征。

图10 后脉冲时间和电荷量分布Fig. 10 Post-pulse time and charge distribution

后脉冲率计算公式为[18]

式中：Amainpilse和N分别代表主脉冲平均光电子数和示波器统计的阳极输出信号波形事例数；Nafterpulse是减掉暗噪声计数之后的后脉冲个数。暗噪声是在没有光照射PMT 的情况下使用相同测量装置测得的信号。图11 为暗噪声和后脉冲波形。

图11 暗噪声与后脉冲波形Fig. 11 Dark noise and post-pulse waveform

关于后脉冲计数Nafterpulse， 需要设定阈值后进行甄别。在软件中甄别过程如下：首先，对信号的电压幅值进行甄别，在示波器记录的波形中寻找电压幅值超过甄别阈的脉冲信号；其次，将幅值过阈信号进行积分得到电荷积分值（V·s），再设定一个电荷积分甄别值，过阈则判定为后脉冲。选择不同的阈值可以得到图12 所示曲线。从图中可以发现在相同的电荷阈值情况下，后脉冲率随着电压阈值的减小而增加。这说明高的电压阈值虽然能够剔除掉一些噪声，但也会误删掉一部分后脉冲信号。在电压阈值恒定的情况下，后脉冲率随着电荷阈值的增加而减少，当电荷阈值降到0.25个单光电子信号的电荷量时，后脉冲率基本保持不变。所以在甄别后脉冲信号时，将电荷阈值设定在0.25 个单光电子信号的电荷量为宜。

图12 后脉冲率和阈值的关系Fig. 12 Relationship between post-pulse rate and threshold

对于前沿时间的分析如图13 所示，PMT 工作电压为1 500 V，初选单电子信号的筛选区间为−2×10−11V∙s～−1×10−11V∙s，在计算获取到波形的前沿时间后，再筛选出r2≥0.98 的拟合数据，即可以得到相应的分布图。在这里可以使用高斯函数进行拟合，其前沿时间在5 ns 左右。结果表明：PMT 的上升时间并不是对称分布的，而是存在一个较长的拖尾。

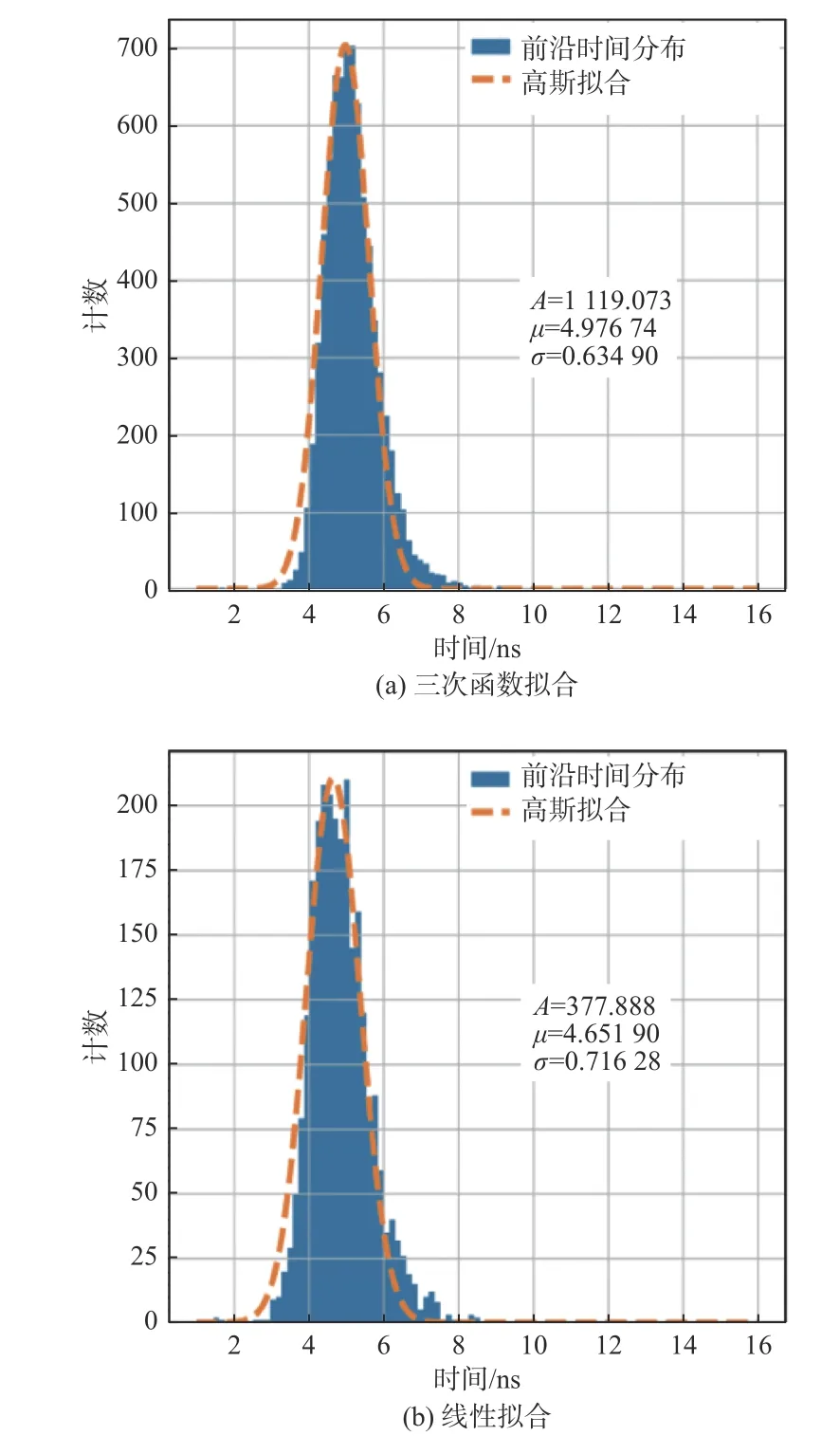
图13 前沿时间分布Fig. 13 Leading-edge time distribution

图13（a）为三次函数拟合前沿得到的时间分布结果，软件中拟合了10 365 个信号波形，三次函数拟合结果中有7 684 个波形的拟合优度在0.98以上，前沿时间为4.98 ns；图13（b）为线性拟合前沿得到的时间分布结果，软件中拟合了10 365 个信号波形，线性拟合结果仅有2 561 个波形的拟合优度在0.98 以上，前沿时间为4.65 ns。结果表明，采用三次函数能够较好拟合脉冲信号的前沿，并得到较为平滑的前沿时间分布。

3.3 基线扣除讨论

图14 基线扣除讨论Fig. 14 Baseline deduction discussion

4 结论

基于Python 开发了一种图形化数据分析系统，核心代码是基于Python 使用多种科学计算的开源库，采用PyQt5 对核心程序进行封装，开发了较为友好的数据分析图形化界面。利用高带宽、高采样率示波器采集并保存PMT 输出的脉冲信号，利用所开发的软件进行离线分析，获得了PMT的脉冲性能参数，包括电荷积分谱、脉冲增益、分辨率、后脉冲率和前沿时间分布，验证了软件的分析功能。与QDC 商用插件测试结果对比表明软件在计算积分电荷谱的功能上与QDC 是等效的，对于缺少QDC 插件的实验室来说可以使用此软件和示波器来替代QDC 的功能；在对后脉冲和前沿时间的分析上，软件功能相对较为丰富，可以容易地实现数据的分析。该软件提供了一种方便的数据分析手段，可以快速实现EM 在脉冲状态下的性能测试评价，满足了实际项目需求。同时，软件具有较好的可扩展性，今后可以根据测试需求开发出新的分析模块。