基于IF-CM-LOF的尾矿坝位移监测数据离群值诊断

易思成 康喜明 吴 浩 胡少华

(1.武汉理工大学安全科学与应急管理学院,湖北 武汉 430070;2.国网内蒙古东部电力有限公司,内蒙古 呼和浩特 010020;3.华中师范大学城市与环境科学学院,湖北 武汉 430079;4.国家大坝安全工程技术研究中心,湖北 武汉 430010)

尾矿库是填筑废弃矿渣的矿山设施,目前我国80%以上的尾矿库采用上游法筑坝,其特点是在初期坝上采用分层填筑的方式形成后期子坝来增加库容[1]。因此坝体位移是尾矿库服役乃至闭库后的一个关键监控指标,目前普遍采用GPS对其进行在线监测[2]。然而,GPS监测过程中由于数据采集频次高且易受到雷击、电压等因素干扰,会在监测数据中出现各种误差;同时尾矿库在受到坝体增高加载、地震、洪水等因素的影响时,可能会出现坝体破坏失稳,发生溃坝事故,从而在监测数据中产生大量异常值(本研究将监测数据中的误差与异常值统称为离群值)。为提高尾矿坝位移监测数据的可靠性,有效发现尾矿坝运行过程中的异常现象,准确识别其位移监测数据中的离群值对于尾矿坝安全监控具有重要的意义[3-4]。

尾矿坝位移监测数据往往呈现非线性特征且难以使用概率分布模型描述,因此基于统计的离群值诊断方法往往适用性不理想[4-5]。孤立森林(IF)作为一种无监督检测方法,对于离群值有着很好的识别能力[6]。张海龙等[7]采用IF算法对经小波变换扣除趋势项的监测数据剩余量进行处理,实现了大坝监测数据离群值的识别;吴志强等[8]利用离散二进制粒子群算法改进IF算法,提升了算法的检测精度和执行效率。该类研究均未能有效解决IF算法仅对于全局敏感、对局部位置识别不佳的问题[9]。CHENG等[10]将局部离群因子(LOF)算法与IF算法相结合,对IF算法处理效果不佳的数据边界位置采用LOF算法进行二次诊断,实现了对局部位置数据的优化处理。然而,该方法仍然存在一定的不足:①IF算法没有明确定义异常概念所对应的异常得分范围;② 将IF与LOF算法结合使用时,对于边界位置的选取具有主观性。因此,如何合理地定义异常得分范围以及选择边界数据仍值得进一步研究。

云模型(CM)是一种实现定量数据与定性概念相互转化的有效方式,能够完成知识与数据之间的不确定性认知转换。部分学者将其运用于尾矿坝变形监测预警,实现了尾矿坝变形预警阈值的有效确定[11]。采用云模型计算复杂数据集的边界范围,并根据计算所得阈值提取候选集用于二次诊断,能有效提高诊断的准确率以及科学性。本研究在现有成果的基础上,使用IF算法对数据集进行初步筛查,将IF计算所得的异常得分作为变量,引入CM对其进行处理,从而完成对异常区间以及数据边界的确定,并由此提取二次诊断候选集,最后引入LOF算法对候选集进行处理。为验证该模型的性能,结合工程实例进行离群值诊断,并与IF模型结果进行对比分析。

1 模型构建

1.1 问题描述

坝体位移GPS监测点及监测信号会不可避免地受到卸料、整平、碾压等坝体施工过程、季节性降雨以及多山环境[12-14]等因素的影响,导致其在数据采集、传输过程中出现各种噪声,从而使得监测数据中出现空白值、粗差和随机误差。空白值通常由传感器失效引起,表现为监测数据的缺失;粗差是指含有粗大误差、严重偏离真实值的数据,常常是由观测过程中的操作疏忽和数据的记录、复制和计算处理过程中的过失错误引起;随机误差则在数据序列中普遍存在,是由各种偶然因素造成的数据小幅度波动现象。当坝体由于渗流作用、洪水漫顶等因素[15]造成不同程度溃坝时,监测数据中也会出现反映这些真实事件的异常值。尾矿坝位移监测数据中的离群值如图1所示。

图1 监测数据离群值分类Fig.1 Outlier classification of monitoring data

IF算法在处理位于边界部分的随机误差时通常效果不佳。本研究引入局部离群因子(LOF)对数据边界位置进行二次诊断。然而数据边界为抽象概念,没有一个定量的指标用以确定复杂数据集的边界范围。因此,需要一种合理有效的方法来确定尾矿坝地表位移监测数据的边界阈值。

1.2 IF基本原理

IF算法是一种基于树的离群值检测算法,其基本原理是不断地对数据集进行分割,直至数据集中的每一个数据都成为孤立点,通过将各点被孤立时距离根节点的路径长度与标准值进行比较,从而判断是否为离群点[6]。IF算法的基本逻辑如图2所示。

图2 IF算法逻辑图Fig.2 Logic diagram of IF algorithm

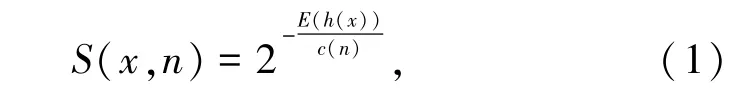
式中,E(h(x))为x的平均路径长度期望值;c(n)为标准平均路径长度。

判断标准定义为

由于尾矿库在线监测系统需要保证监测到整个尾矿坝全天候的运行情况,因此其监测范围广、测点布设较多、监测周期极短,从而导致数据量非常庞大。IF算法能够通过子采样建立局部模型,适用于尾矿库的大规模监测数据。

1.3 CM-LOF局部优化诊断

IF算法虽然实现了对每个数据值赋予异常得分,然而式(2)中对于离群值的判断只给出了一个模糊的概念,对得分处于(0.5,1)区间的数据点并没有给出一个确定的阈值来评判其是否为离群值。因此,本研究引用CM算法确定(0.5,1)区间内的异常得分阈值,并根据计算结果选取候选集,采用LOF算法对候选集进行优化计算。

CM算法中逆向云发生器可以完成定量数据向定性概念的转化,将IF算法得到的异常得分S(x,n)位于(0.5,1)区间内的值导入一维逆向云发生器进行建模后生成云模型,根据云数字特征值进行区间划分从而确定异常阈值,云模型如图3所示。

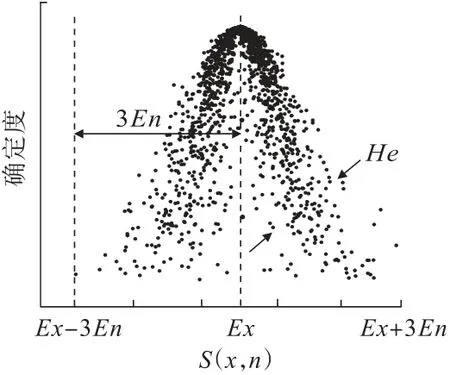
图3 云模型示意Fig.3 Schematic of cloud model

图3中,Ex,En,He分别代表期望、熵、超熵3个数字特征值。根据文献[16]的相关计算结果,位于(Ex-3En,Ex-2En)和(Ex+2En,Ex+3En)区间中的云滴对“正常”概念的贡献度仅有4.3%,落在区间外的云滴对表征的定性概念几乎无贡献。因此本研究选取(Ex+2En,1)区间为显著异常区间,其中的数据点认定为IF算法识别的异常点;(Ex,Ex+2En)区间为不确定区间,将该区间内的数据作为候选集,引入LOF算法对其进行离群值优化诊断。LOF算法通过计算某样本点x的局部离群因子(LOF值)来判断该点是否为离群值,LOF值越大,表明该样本点偏离局部中心的程度越多,越有可能为异常点[17]。LOF值定义为

式中,Nk(x)为x的第k距离;lrdk(x)为x的局部可达密度。

通过下式判断x是否异常:

基于2017年河北省矿产资源开发利用基本情况与特点，对比全国矿产资源开发利用情况[5-8]，对2017年河北省矿产资源开发利用情况总结如下。

1.4 算法流程

LOF算法通过对数据集中的每个点进行计算而有着较高的准确率,但是其计算量十分庞大,需要的存储空间及时间复杂度高,不适用于大规模数据的检测。通过IF算法对尾矿库位移监测数据进行整体筛查、采用CM算法确定边界部分数据候选集后,再使用LOF算法对少量的候选集数据进行离群值诊断,不仅能有效降低算法计算量,还能够提高边界部分离群值的诊断率。IF-CM-LOF模型如图4所示。

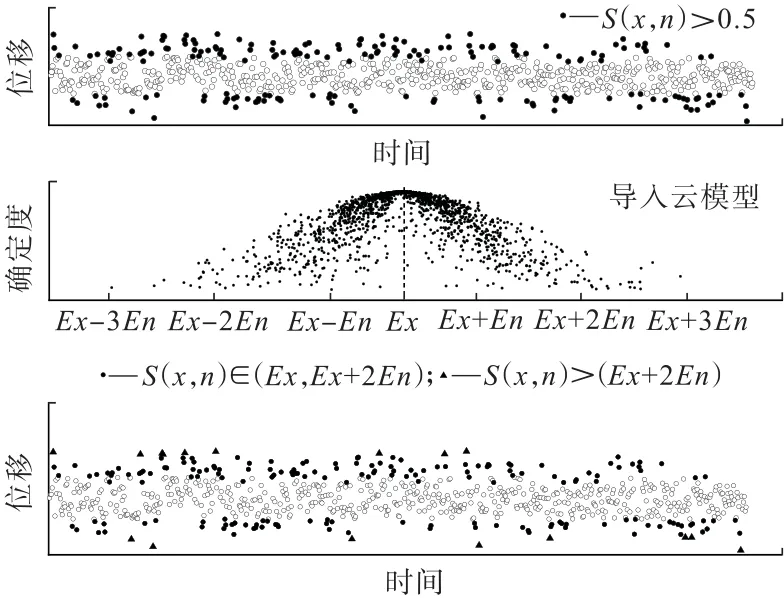
图4 IF-CM-LOF模型示意Fig.4 Schematic of IF-CM-LOF model

具体操作步骤为:①导入尾矿坝位移监测数据,构造孤立树及孤立森林,计算标准平均路径长度c(n)及各样本点的平均路径长度期望E(h(x)),归一化处理得到异常得分S(x,n);②根据式(1),导出S(x,n)位于(0.5,1)区间内的数据,采用CM算法构建云模型,并根据云模型数字特征值选取阈值,取(Ex,Ex+2En)区间内的数据作为离群值候选点;③运用LOF算法处理候选点,计算各点的LOF值,根据式(3)确定随机误差。IF-CM-LOF算法的详细流程如图5所示。

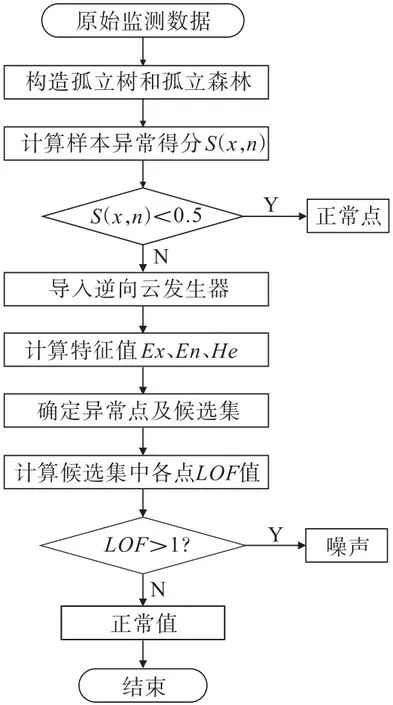
图5 IF-CM-LOF算法流程Fig.5 Flow of IF-CM-LOF algorithm

2 工程应用

2.1 工程概况

湖北省某尾矿库为山谷型尾矿库,采用上游式筑坝方式。初期坝为透水堆石坝,坝长146.45 m,坝顶宽5 m,坝顶标高50 m。每级子坝高度为3 m,现已堆积至 15期子坝,堆积标高为 95 m,总库容达1 469.34 m3。该尾矿库于2014年完成了在线监测系统的投运,通过GPS技术对坝体表面位移进行在线监测,共布设了12个监测点。本研究选取该尾矿坝同高程GB-1、GD-2以及同截面GB-2、GB-3共4个监测点2017年1—6月的位移监测数据作为测试样本,来验证模型的性能。尾矿坝位移监测点分布如图6所示。

图6 某尾矿坝位移测点分布Fig.6 Distribution of displacement measuring points of a tailing dam

2.2 模型诊断

为验证模型对离群值的诊断效果,本研究在4个测点的监测数据中分别设置部分数据为离群点,其类型、数量以及分布如表1、图7所示。

表1 各测点的离群点类型及数量Table 1 Type and number of outliers at each measurement point

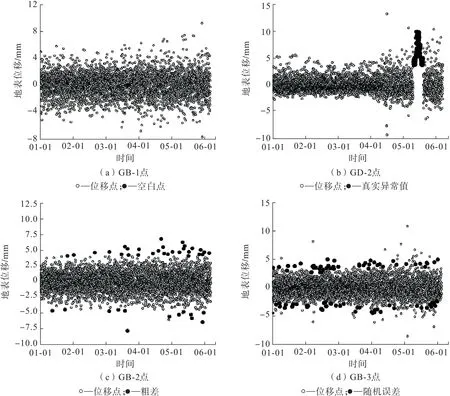
图7 某尾矿坝各测点地表位移及离群值分布(2017年)Fig.7 Surface displacement and outlier distribution at each measuring point of a tailing dam (2017)

图7(a)设置30个连续的空白值,用于模拟监测过程中由于断电等因素引发的监测设备停止运行状况;图7(b)设置100个连续的真实异常值,用于模拟尾矿坝发生溃坝情况下的数据监测状况;图7(c)、图7(d)为在全时间序列下设置的43个离散粗差以及90个随机误差,用于模拟监测设备在各种复杂环境条件下所产生的噪声。

本研究使用IF算法对数据进行离群值诊断,由于算法给出的异常区间范围不明确,因此本研究选择异常得分范围为(0.7,1)内的点为离群点,结果如图8所示。

图8 各测点IF诊断结果Fig.8 IF diagnosis results at each measurement point

由图8(a)、图8(c)可知:IF算法在处理空白值和粗差时有着良好的识别效果,体现了其对于全局敏感的特性。图8(b)显示在处理连续异常变化的真实异常值时,IF算法识别结果不完整,出现了大量的漏判现象。这是由于算法没有准确地给出异常区间所对应的得分,因此仅凭经验选取的异常得分范围不够合理,无法囊括全部异常点。图8(d)反映了IF算法在处理边界数据时,对于噪声所带来的随机误差会出现大量的漏判,这也是由于没有合理选取异常区间范围所致。此外,即使扩大异常得分范围,也会出现大量的误判现象。其原因是IF算法在处理一维监测数据时,会将异常数据的筛选问题抽象为数据出现的频次问题[18],而不会考虑数据在时间序列上的分布情况,使得某一个位移数据对应的全时间序列下的数据点都被识别为离群点。因此,为准确判断边界部分的随机误差,需要对其进行二次诊断。

引入的CM模型能够合理地选取边界数据集,并解决IF算法异常区间的确定问题。提取IF算法异常得分处于模糊区间(0.5,1)内的数据并导入逆向云发生器,结果如图9所示。

图9 各测点IF得分云图(2017年)Fig.9 IF score cloud diagram of each measuring point (2017)

由图9可知:4个测点的期望值Ex均在0.6附近,说明IF得分处于0.6附近的点为该样本集的集中部分。以Ex+2En作为异常得分阈值边界点,选取(Ex,Ex+2En)区间作为二次诊断的候选区间,计算结果见表2。

表2 各测点CM特征值计算结果Table 2 Calculation results of CM characteristic values at each measuring point

候选集分布如图10所示。

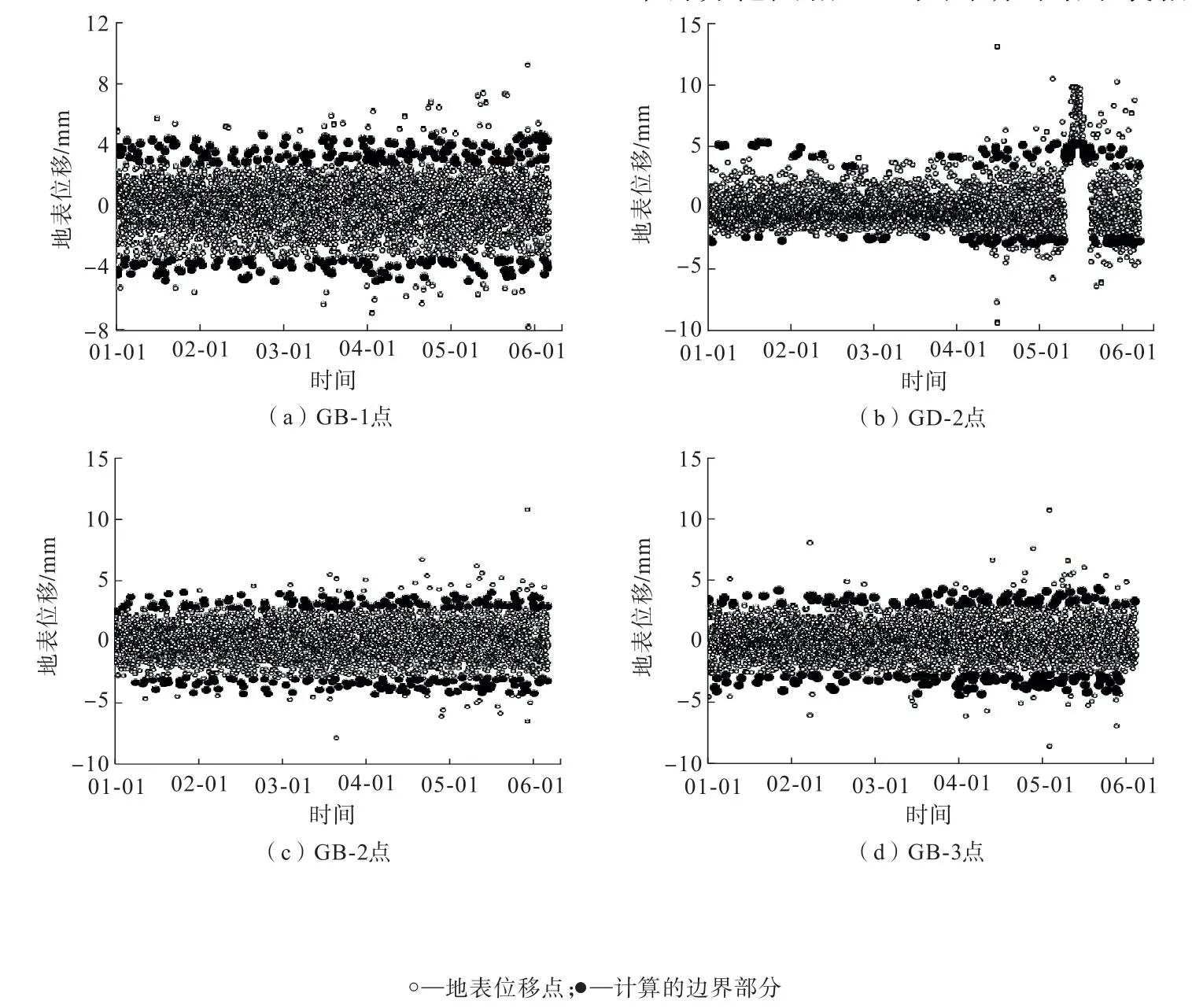
图10 各测点候选集数据分布(2017年)Fig.10 Data distribution of candidate sets at each measuring point (2017)

由图10可知:在引入CM对IF得分进行阈值计算后,根据云数字特征值选取的候选集区间能够准确定位到复杂数据集的边界,从而完成对边界部分数据的提取,实现了定量的IF得分数据向定性的“边界”概念转化。

结合IF算法一次诊断结果,引入LOF算法对候选集进行离群值的二次诊断,实现对边界部分数据中随机误差的识别,结果如图11所示。

由图11(a)、图11(c)可知:该模型对空白值以及粗差的识别效果保留了IF算法本身所具有的优越性;图11(b)反映出经过CM计算阈值后所确定的异常得分范围相比经验判断的结果囊括了更多的真实异常值,体现出了该模型的科学性与合理性;图11(d)体现出该模型对于边界部分随机误差的识别效果较好。

分别计算分析了IF-CM-LOF模型与IF模型对于预先所设离群值的检验效果,结果见表3。

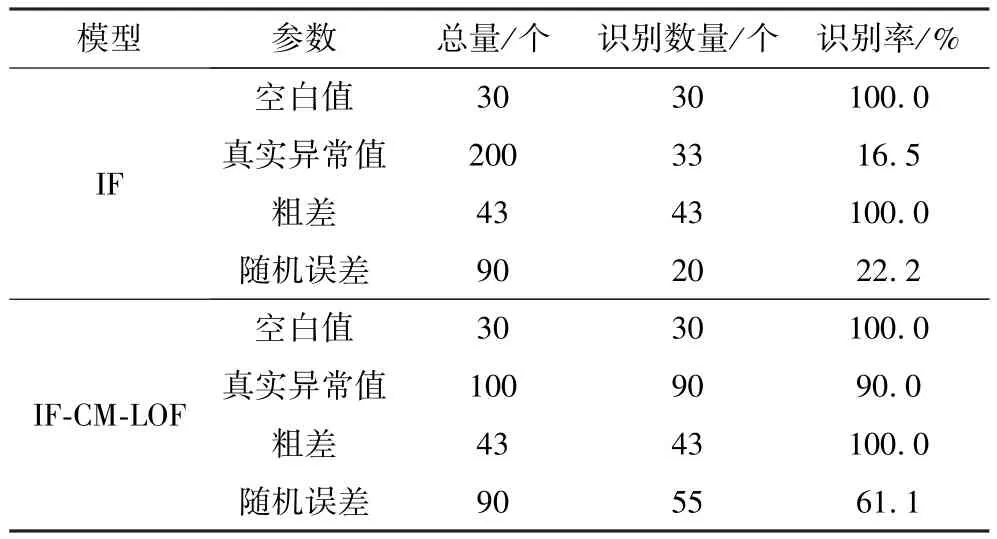
表3 两种模型离群值诊断结果Table 3 Outlier diagnosis results of the two models

由表3可知:IF对空白值以及粗差的识别效果较好,识别率均达到100%,体现出该算法对于全局离群点敏感的特性;然而对于真实异常值以及随机误差,识别率仅有16.5%和22.2%,主要原因是IF得分异常区间不明确,使得仅凭经验判断的得分阈值无法覆盖全部离群点,从而出现大量漏判。在引入CM对边界数据进行定位提取并使用LOF对其进行二次诊断后,真实异常值和随机误差的识别率分别提高到至90%和61.1%,体现出CM对边界范围确定的可行性以及模型的整体优越性。

3 结 论

(1)针对IF算法对于边界位置数据异常识别结果的模糊性和不确定性问题,本研究通过逆向云变换将“边界”这一抽象概念的定位问题转化为边界阈值的计算问题,实现了复杂数据集边界位置的确定。通过进一步引入LOF算法对边界部分数据离群值进行二次精确诊断,弥补了IF算法对于边界位置处理的不足。

(2)工程实例验证发现,IF-CM-LOF模型对于真实异常值以及随机误差的检测率达到90%以及61.1%,明显优于IF模型的16.5%和22.2%,反映出该模型的优越性。

(3)目前,IF-CM-LOF模型仅有助于提高对离群值的检出率,无法判断其所识别的离群值是否为噪声或真实异常值,因此对于离群值的类型判定仍需进一步研究。