渑栾高速采空区路段建设场地稳定性评价研究

杨 锋 王 亮 郭庆彪 万战胜

(1.河南省交通规划设计研究院股份有限公司,河南 郑州 450000;2.安徽理工大学空间信息与测绘工程学院,安徽 淮南 232001)

紧张的土地资源现状制约着资源型城市的转型发展,而对采空区上方土地资源进行有效地开发利用是缓解这一紧张局面的有力措施[1]。由于老采空区地表具有长期的残余变形特征,可能会破坏拟建工程的稳定性,影响其安全使用。因此,在对老采空区上方土地资源进行开发建设时,有必要对建设场地进行科学地稳定性评价。

以往老采空区上方建设场地稳定性评价方法主要有力学解析法、工程地质类比法、综合评价法等,该类方法或侧重定性评价,或考虑的评价指标不够全面,进而在不同程度上影响了评价结果的准确性[2-3]。近年来,随着非线性理论的发展,不少专家学者将其应用于采空区上方建设场地的稳定性评价中。王尧等[4]利用事故树理论建立了采空区稳定性评价模型,通过对比各影响因素的发生概率,可以分析出采空区上方建筑物的稳定性;耿宏波等[5]在突变理论的基础上采用突变级数法,根据各评价指标的相对重要性,获得了采空区稳定性的评价结果,为采空区上方建设场地的开发利用提供了有效的科学指导;陈文军等[6]通过构建建设场地稳定性评价体系,收集了已有的场地稳定性评价数据并进行聚类分析,最终确定出待评价场地区域的稳定性状态;车安刚等[7]通过随机介质理论预测了老采空区的稳定性状态,并将其应用于工程实践中,评价结果与实际吻合性较好。王彤标等[8]采用专家打分法和AHP法归纳了稳定性评价指标的主控因素,建立了适用于贵州山区煤矿采空区稳定性评价模型,对于类似的采空区场地稳定性评价具有一定的借鉴意义。以上方法对于建设场地的稳定性评价有着一定的指导意义,但是由于建设场地的评价指标具有模糊性、随机性,导致上述方法的应用具有一定的局限性,且评价指标权重的确定过于依赖个人经验,使得评价结果的可靠性有待提高。

针对以上问题,本研究以模糊评判为中心,综合考虑定性、定量等多个指标,并结合云模型理论对采空区建设场地的稳定性进行评价。以渑栾高速采空区路段建设场地为例,首先从水文地质条件、开采技术条件、场地变形特征和外界扰动4个方面选取了12个指标构建了该区域的稳定性评价模型;然后基于三角模糊层次分析法确定各指标的权重,再结合正态云模型理论,将研究区域的评语集转换为数字特征,最终得出研究区域的稳定性等级,实现了定性概念转换为定量信息,在一定程度上避免了人为主观因素的影响。

1 采空区建设场地稳定性评价体系构建

采空区建设场地的稳定性评价是一项极为复杂的系统问题,受多种因素耦合影响。为科学、准确、全面地评价煤矿老采空区建设场地稳定性,本研究从水文地质条件、开采技术条件、场地变形特征和外界扰动4个方面,共选取包括构造复杂程度、覆岩力学强度、采空区深厚比、潜在残余变形值等12个评价指标,构建了II级评价层次模型,如图1所示。各指标对采空区建设场地稳定性的影响机理[9-10]进行如下所述。

(1)构造复杂程度。矿井地质构造的复杂程度主要通过断层密度来影响建设场地的稳定性,断层密度值过高会破坏岩层之间的连续性,并释放大量的弹性变形能存在于断层或岩体裂隙中,从而使建设场地的稳定性受到影响。

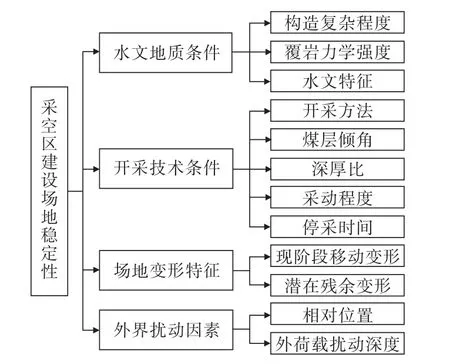
图1 采空区建设场地稳定性评价指标体系Fig.1 Evaluation index system of stability of goaf construction site

(2)覆岩力学强度。覆岩力学强度为采空区覆岩中硬质岩与软质岩厚度的比值。比值越大,煤层顶板越不易垮落,且垮落后岩石块较大,存在较大的空隙,可发生残余变形的空间大,从而导致建设场地的稳定性较差;比值越小,垮落速度越快,未来可发生残余变形的空间小,建设场地的稳定性较高。

(3)水文特征。地下水与岩土之间的相互作用对岩土体有着润滑功能,会导致结构面的抗剪强度衰减,从而使岩土软化、力学性能大大减弱。此外,地下水的化学作用(如溶解和溶蚀)会增大岩体之间的空隙率以及渗透性,降低采空区围岩的稳定性,对于建设场地的稳定存在一定的影响。

(4)开采方法。开采方法的不同,对上方建设场地的稳定性影响也有所区别。使用长壁式方法开采时,通常会造成岩石冒落和发生开裂性破坏,并会引起地表出现塌陷,导致上方建设场地的稳定性较差;用充填法采煤,对覆岩的破坏程度较小,一般情况下只会引起开裂性破坏而无冒落性破坏,对于建设场地的稳定影响较小;采用部分开采的采煤方法可以有效地控制覆岩与地表移动,可以保障上方建设场地处于稳定状态。

(5)煤层倾角。煤层倾角为煤层层面与水平面的夹角。煤层倾角越大,不仅会加剧地表的不均匀沉降、增大地表的水平变形,还会造成采空区覆岩应力分布趋于复杂、内部裂隙与节理更加发育,从而降低建设场地的稳定性。

(6)深厚比。采空区深厚比为煤层开采深度与开采厚度的比值。深厚比越大,对覆岩变形的破坏程度越小,其对于上方建设场地的稳定性影响也就越小;深厚比越小,对于覆岩的变形破坏会更加激烈,覆岩破坏将会迅速传递到地表,影响上方建设场地的稳定性。

(7)采动程度。采空区的采动程度不同,其上方建设场地的稳定性存在较大的差异性。若采动为充分采动,采空区的覆岩破坏已较为充分,且覆岩和地表所产生的移动变形较大,此时建设场地的稳定性较高;若采动为非充分采动,此时的采空区覆岩破坏不充分,在外界荷载的扰动下会诱发老采空区产生“活化”现象,进而降低上方建设场地的稳定性;当采动属于极不充分采动时,采动覆岩被破坏的程度较小或未被破坏,此时对上方建设场地的稳定性影响微乎其微。因此,采动程度与采空区上方建设场地的稳定性并非呈线性相关关系,而是随着采动程度的增大,建设场地的稳定性由高变低再转变为高的过程。

(8)停采时间。开采时间越长,采空区所发生的移动变形越充分,地表残余沉降就越小,建设场地的稳定性则越高;如果采空区处于衰退期或者残余变形阶段,其残余变形量依然很大,此时建设场地是不稳定的。

(9)变形机理。现阶段沉降变形会引起地表产生不均匀沉降、倾斜甚至开裂变形,对于上方建设场地的稳定性存在较大的影响。残余移动变形与建设场地的稳定性直接相关,通过破坏岩层的连续性,在断层处不断积累弹性势能,诱发采空区“活化”,进而诱发建设场地的塌陷失稳,降低其稳定性。

(10)相对位置。相对位置为建设场地到采空区中央的距离与采空区1/2长度的比值。当建设场地位于采空区中央上方或采空区边界之外时,地表残余变形对其影响不大,该建设场地的稳定性较高;当建设场地位于采空区边界上方时,由于该区域存在较多的空洞、空隙,可能会产生较大的残余变形,从而降低了建设场地的稳定性。

(11)外荷载扰动深度。外荷载越大,其扰动深度越深,当达到一定程度时,其采空区内部岩体的平衡状态会受到扰动而再次产生失稳和破坏,极大地影响了采空区上方建设场地的稳定性和安全性。

2 三角模糊函数确定指标权重

考虑到评价过程的复杂性与不确定性,本研究采用三角模糊函数法确定评价指标的权重。通过组织邀请专家,对同级指标进行两两比较,假设每位专家的权威性一致,结合0.1～0.9的模糊标度法(表1)[11],可得各专家对评价指标的重要性倾向程度,进而构建三角模糊判断矩阵。

表1 模糊标度Table 1 Fuzzy scale

采用模糊层次分析法计算各指标权重的步骤[12-13]如下:

(1)构建递阶层次结构。分析影响采空区建设场地稳定性的因素并进行分层,递阶层次结构分为目标层、准则层和方案层,同时标明上一层元素与下一层元素之间的关系。

(2)构造模糊互补判断矩阵。为客观地评判各个指标的权重,本研究邀请3位专家来构建三角模糊互补判断矩阵,并对所构建的矩阵进行模糊化处理,以消除专家评价偏好或者偏好程度过高对稳定性评价的不良影响,其模糊化原理如式(1)所示。设三角函数M(l,m,u)的期望值E(M)定义为

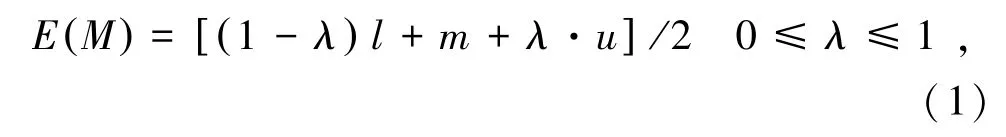
式中,l、m、u分别是专家给出的两个评价指标相对重要度的模糊区间上界、中界和下界;λ为模糊化系数,取值与决策者的愿意承担风险指数有关。当0≤λ<0.5时,表示决策者愿承担风险;当λ=0.5时,表示决策者对于风险持中立态度;当0.5<λ≤1时,表示决策者不愿接受风险。

(3)层次单排序及一致性检验。层次单排序是指依据三角模糊互补判断矩阵,对于上一层某指标而言,本层次与之对应的指标重要性次序的权重计算过程。其原理是对模糊化后的矩阵求解各级模糊互反判断矩阵,并对其进行一致性检验。一致性检验计算公式为

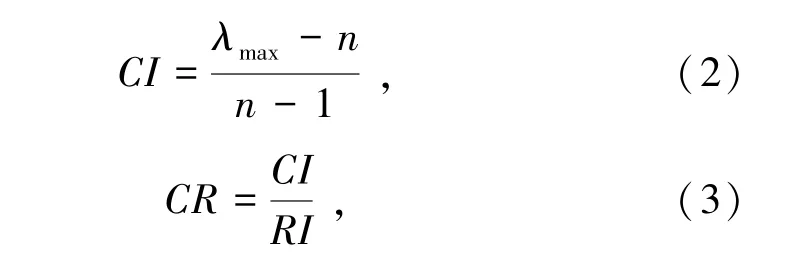
式中,CI为一致性指标值;λmax为模糊互反判断矩阵的最大特征根;n为指标个数;CR为一致性比例;RI为随机一致性指标,取值如表2所示。

表2 随机一致性指标RI的取值Table 2 Values of random consistency index RI

当n=1,2时,RI=0,通常认为一、二阶判断矩阵总满足一致性;当n≥3时,则需要根据CI和RI值计算CR,若CR<0.1时,判断矩阵通过一致性检验;反之,则不通过,需对判断矩阵进行修正。

(4)层次总排序及一致性检验。层次总排序是指依据从最高层次到最低层次计算的原则,计算出同一层次内所有指标相对于上一层次的重要性排序权值。总层次排序随机一致性检验可由下式计算:

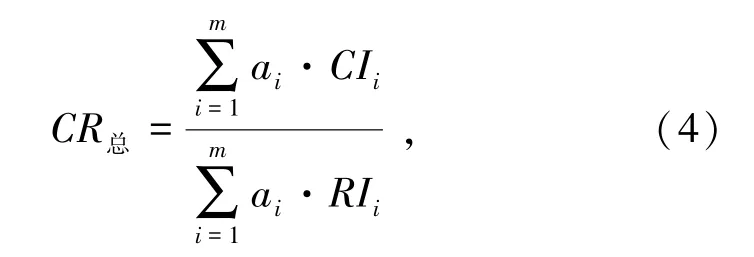
式中,ai为指标Ai所对应的层次单排序权值;CIi为相对Ai单排序的一致性指标;RIi为相对Ai单排序的平均随机一致性指标。当CR总<0.1时,层次总排序通过一致性检验,可以计算各指标的权值。

(5)指标权重计算。设通过一致性检验的三角模糊判断矩阵为A=(a ij)n×n,其中a ij= (alij,amij,auij)为三角模糊数。利用下式可求出三角模糊数权重向量W=(W1,W2,…,W n)T:

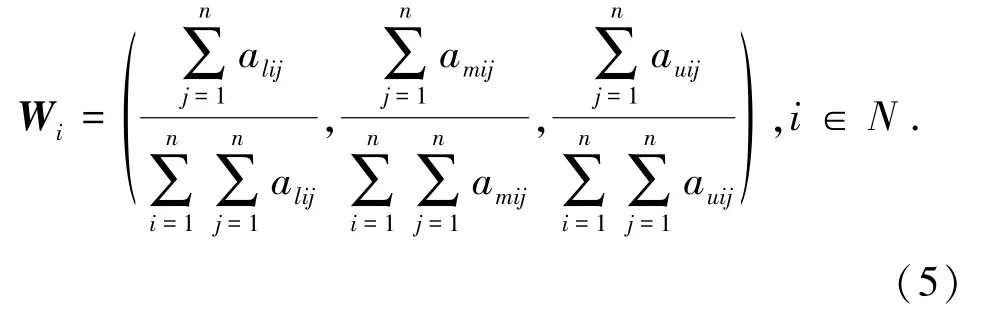
3 基于云模型的采空区建设场地稳定等级确定

3.1 云模型基本理论

云模型[14]是由李德毅院士提出的一种用于实现定性概念与定量信息之间相互转换的模型,目前已在边坡稳定性评估、空气质量评价、岩爆预测等多个领域得到应用,并展现了广阔的发展前景[15]。

Ex、熵En和超熵He,通过这3个数字特征能够实现对定性概念和定量特性的分析。在对老采空区进行稳定性评价时,常采用正向高斯云发生器来构建定性与定量之间的联系[16]。正向高斯云发生器的具体算法步骤为:① 随机生成以En为期望、He2为方差的正态数En′;② 随机生成以Ex为期望、En′2为方差的正态数xi;③ 计算,其中(x,μ(x))为论域中的一个云滴;④重复步骤①至③,直至产生足够多的云滴。

3.2 稳定性评价指标云化方法

由于对老采空区的稳定性评价具有模糊性和不确定性,因此需要通过正向云发生器对评价指标进行云化,即将研究区域各评价指标的评语集转换为云模型的数字特征,从而实现定性评价与定量评估之间的相互转换[17]。具体步骤如下:

(1)采取云模型描述各评价指标的评语集。对每个评语集进行描述常采用一维正态云的方法,需先将评语集的取值区间分为s个子区间,其中第k个区间对应的评语集为(不稳定、欠稳定、基本稳定、稳定),再根据式(6)、式(7)和式(8)和每个区间的上下限值计算每个评价指标云模型的3个数字特征SC(Exk,Enk,Eek)(k=1,2,…,n),公式为

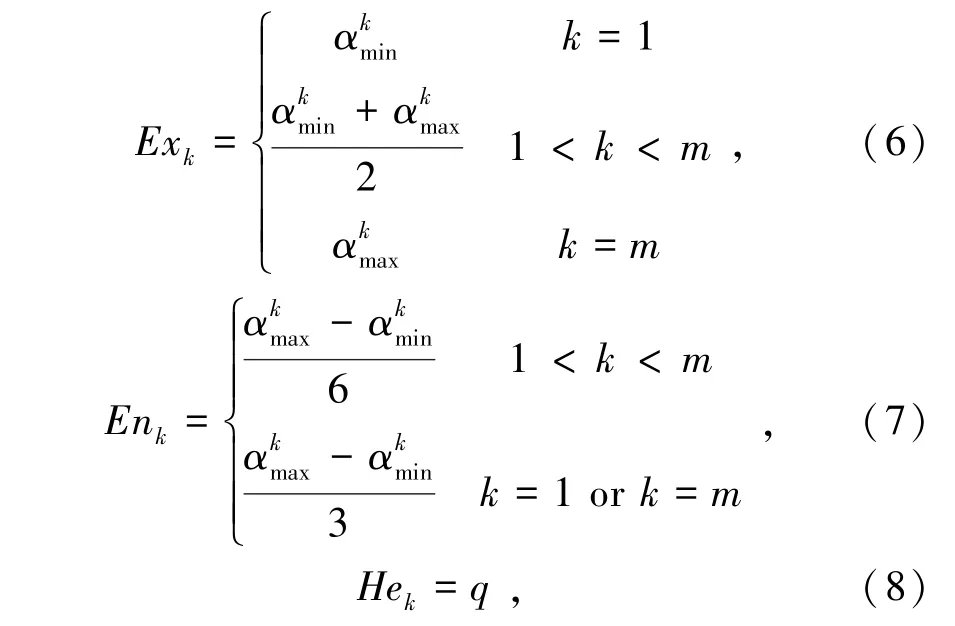
式中,q为常数,本研究q=0.5。

(2)一般情况下,称下一准则层各个指标的云模型为其上一准则层指标的基云,上一准则层的指标可以由其基云综合而形成。采用式(9)可以对二级准则层进行综合计算,采用式(10)可以对一级准则层进行综合计算。

式中,wi为每个单独指标的权重;n为单项影响因素的数量。

(3)用正向云发生器计算每个评价指标的实际云模型,与其相对应的标准云模型进行比较,最终得到每个采空区的评价结果。

本研究依据《采空区公路设计与施工技术细则》(JTG/T D31-03—2011)[18]将老采空区分为稳定、基本稳定、欠稳定、不稳定4个等级,对应的分值区间分别为[0,25),[25,50),[50,75),[75,100],根据式(6)至式(8)计算可知,各评价等级对应的云数字特征分别为SC稳定(0,8.33,0.5),SC基本稳定(37.5,4.17,0.5),SC欠稳定(62.5,4.17,0.5),SC不稳定(100,8.33,0.5)。 其稳定性标准云生成图如图2所示。

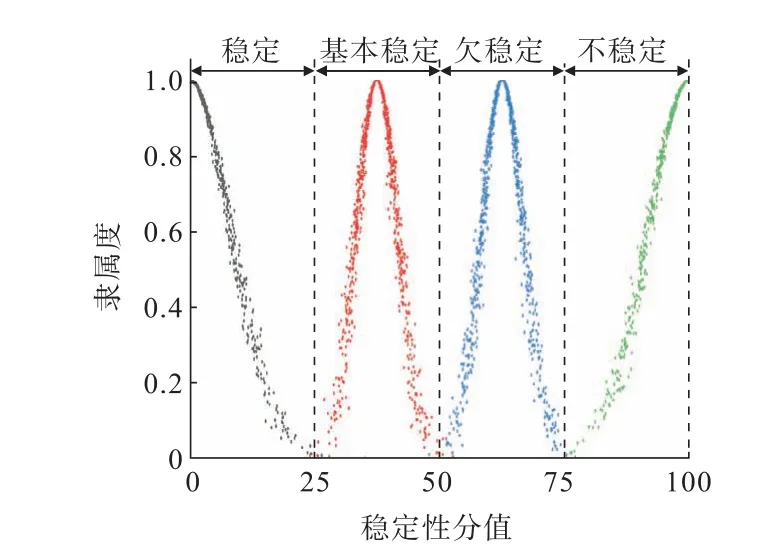
图2 采空区稳定性的标准云图Fig.2 Standard nephogram of goaf stability

4 实例分析

4.1 工程概况

渑池—栾川高速公路起点位于三门峡市渑池县境,北接在建的山西垣曲至渑池高速公路并与连霍高速交叉,向南经洛阳市宜阳县西、洛宁县东、嵩县西,在栾川县潭头镇与已建成通车的洛嵩栾高速相接,路线全长为40.082 km。其中渑池至洛宁段K4+800～K8+150区间穿越千秋煤矿,井田上方路线长度总计3.35 km,路线走廊与下伏采空区和储煤区的相对位置关系见文献[19-20]。

结合所收集的资料进一步分析,可得沿线下伏各工作面的回采详细信息见表3。

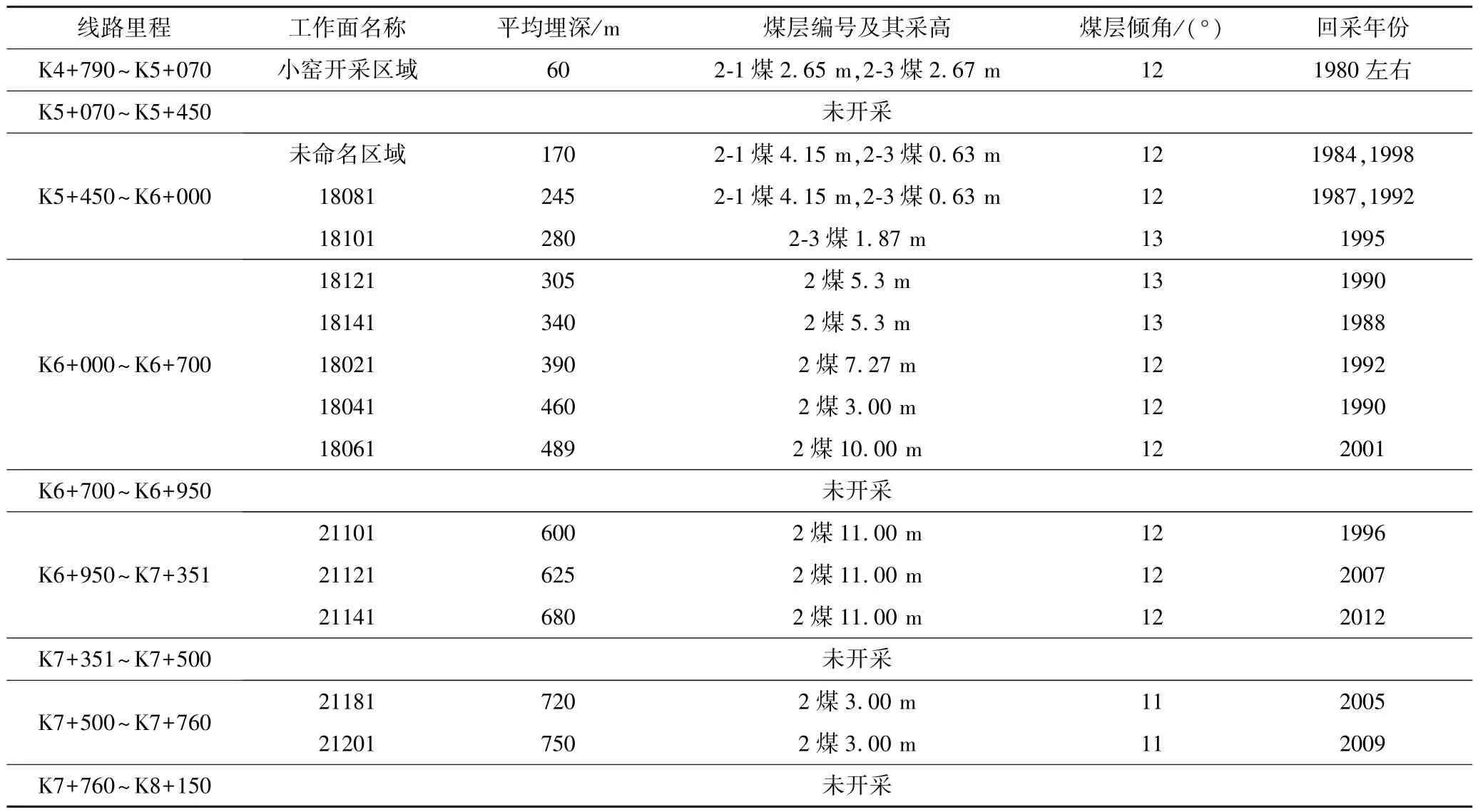
表3 渑栾高速采空区路段下伏工作面回采信息Table 3 Mining information of the working face under the goaf section of the Mianluan Expressway

结合表3以及其他资料,可以给出该研究区域各影响因素的评语集见表4。

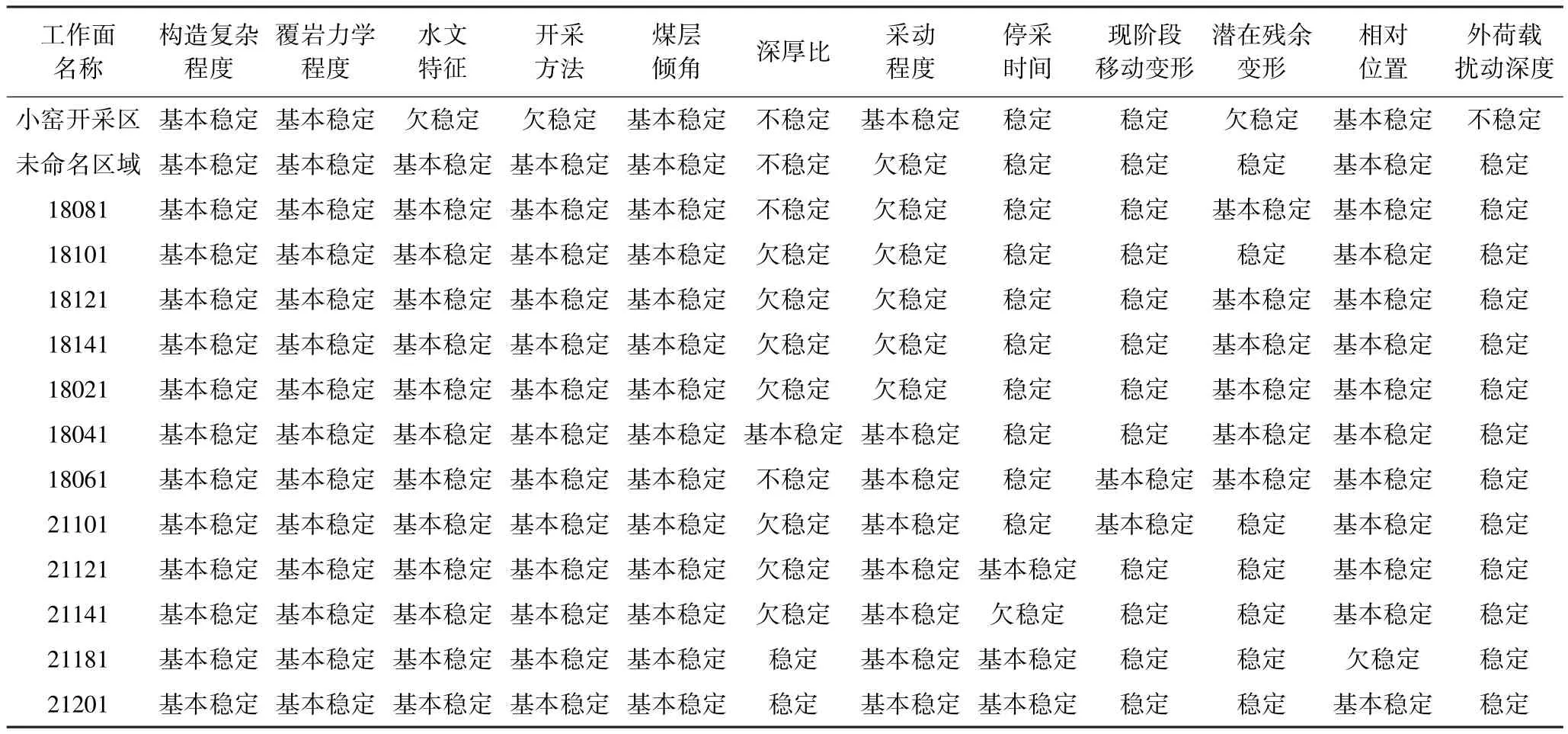
表4 渑栾高速各采空区稳定影响因素评语Table 4 Comments on influential factors of stability in goaf of the Mianluan Expressway

4.2 构造模糊互补判断矩阵确定各指标权重

本研究邀请了3位分别来自中国矿业大学、安徽大学和安徽理工大学的专家,对同级指标进行两两比较。在判断标度选择上,本研究采用表1所示的0.1～0.9的模糊标度法。具体构造过程如下:

(1)对一级的4个指标构建三角模糊数互补判断矩阵,如式(11)所示。

根据式(1)对C1进行去模糊化处理,以尽可能消除专家评价偏好或偏坏程度过大的不良影响,本研究取λ=0.5,即E(C1)=(l+2m+u)/4,再对模糊化后的矩阵求解模糊互反判断矩阵,并进行一致性检验。公式为

通过MATLAB计算可得,λmax=4.001,则:,通过一致性检验。则利用式(5)计算一级的 4 个指标权重W1、W2、W3、W4分别为

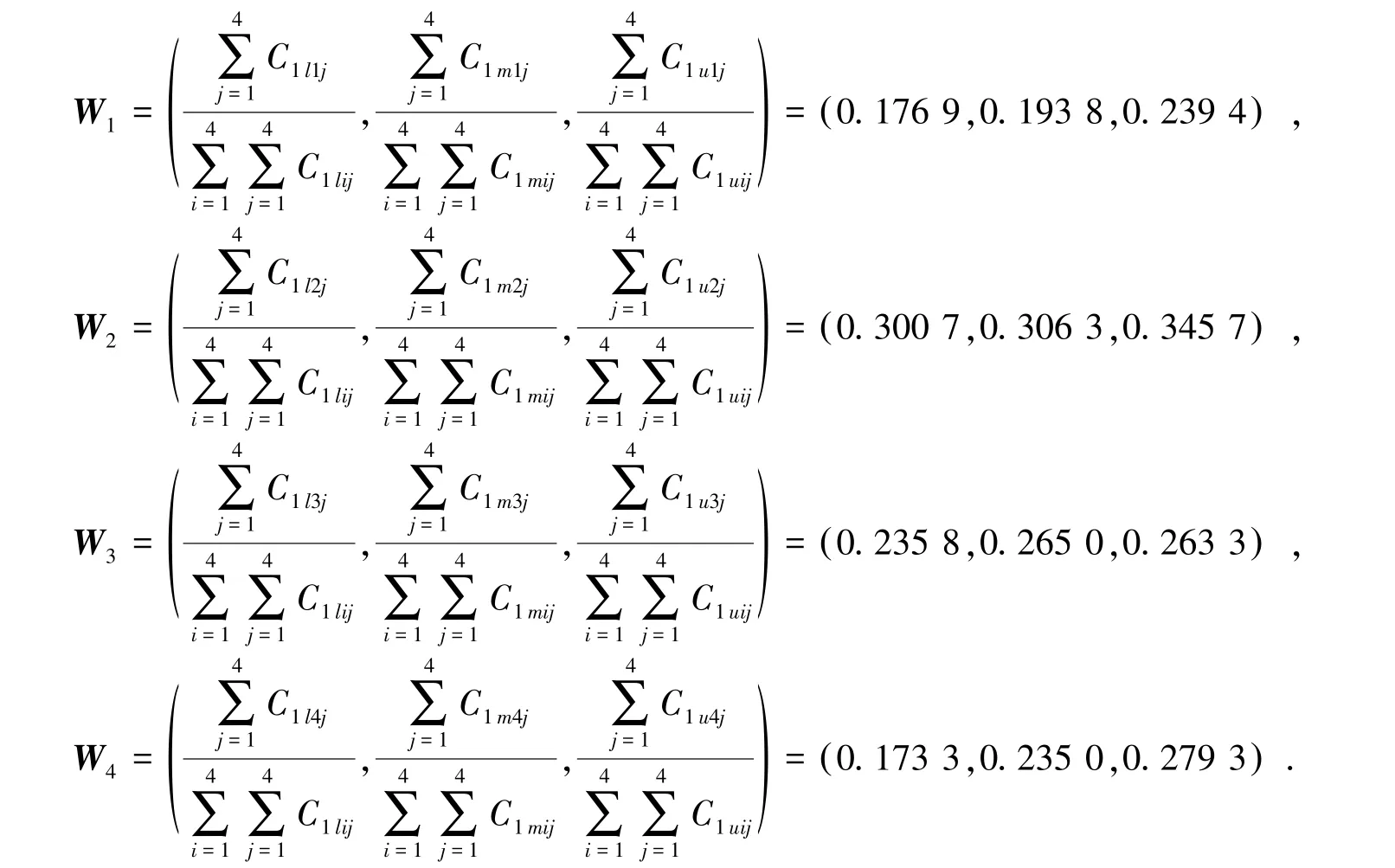
利用式(1)对W1、W2、W3、W4去模糊化并标准 化处理得到一级指标标准化权重向量为

(2)利用一级指标权重确定的方法,构造一级指标所对应的二级指标的三角模糊数互补判断矩阵,结果如下:

利用式(1)对C21、C22、C23、C24去模糊化并进行一致性检验。其中,层次单排序中,

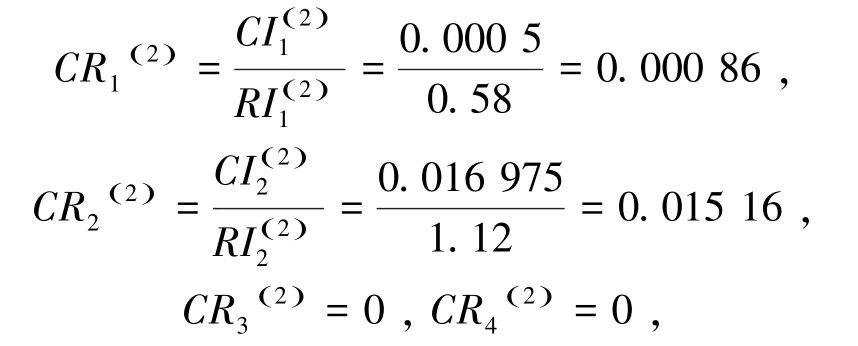
均通过一致性检验。

为了进一步得到各评价子项目对总目标的排序权向量,需要对层次C进行层次总排序的一致性检验。经计算,

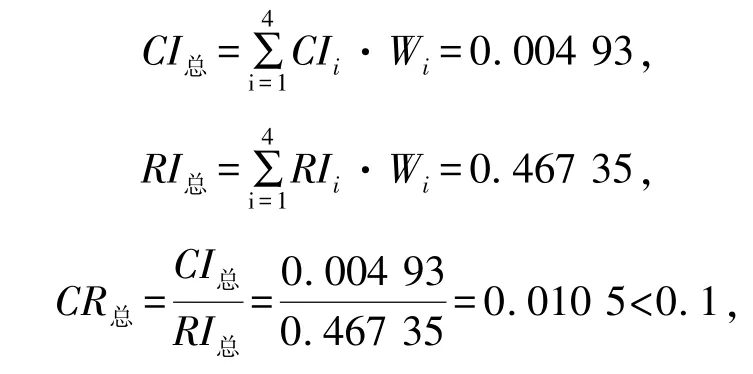
因此得到的层次总排序满足一致性检验。

利用式(5)计算各级指标权重,再根据式(1)去模糊并标准化处理后所得结果见表5。

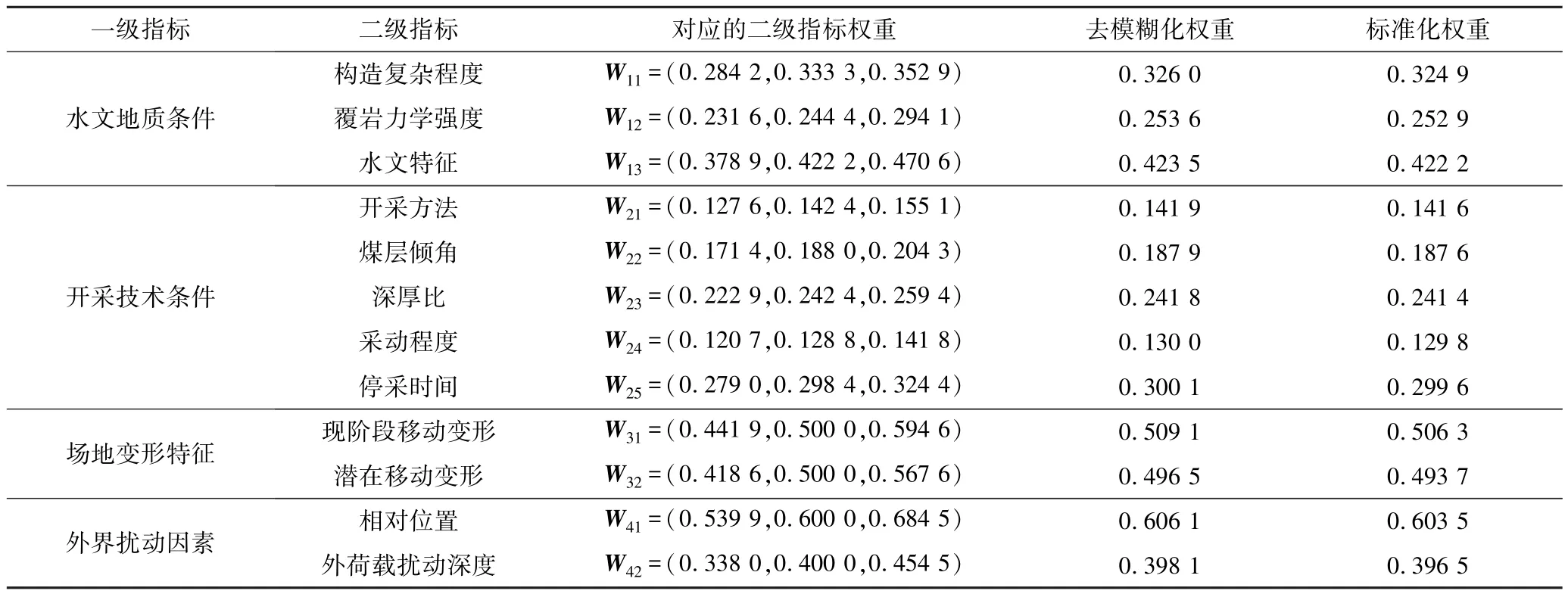
表5 二级指标权重向量Table 5 Weight vectors of the secondary index

4.3 采空区建设场地稳定等级确定

以渑栾高速采空区的小窑采空区为例,专家对小窑采空区各影响因素的评语集见表4,将其转换为云数字特征,再结合表5中的指标权重,得到小窑采空区的稳定性评价指标云特征及权重,见表6。

根据式(6)至式(8),通过计算可以得出小窑采空区一级指标的云数字特征,见表7。

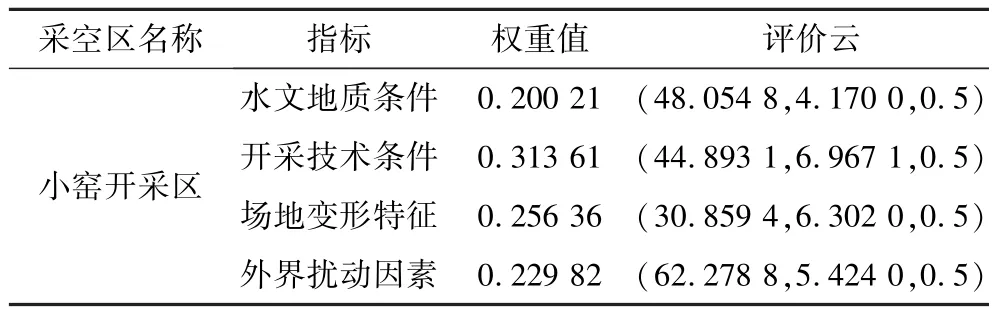
表7 小窑采空区一级指标评价云及权重Table 7 Evaluation cloud and weight of the first grade index in the goaf of small kiln

由表7的数据再结合式(10)可以求得小窑采空区的数字特征为(45.171 7,23.527 7,0.5),图 3为小窑采空区稳定性云与标准稳定性云的对比图。

由图3可知:小窑采空区的综合模型云滴主要落在基本稳定和欠稳定区域,且期望值为45.171 7,统计落在每个区域的云滴数,结果见表8。由表8可知:落在“基本稳定”区域内的云滴数最多,其次是落在“欠稳定”区域。由此可知:小窑采空区的稳定性级别为基本稳定,但程度更偏向“欠稳定”级别。

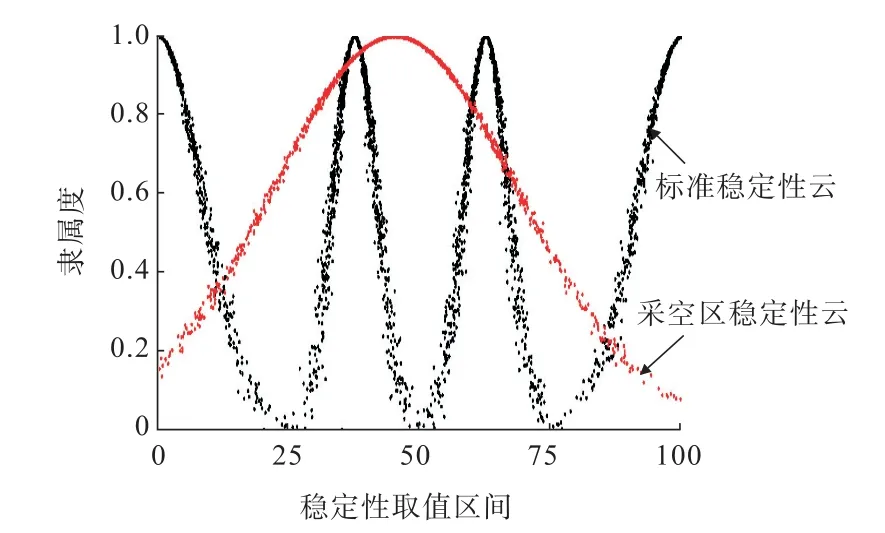
图3 评估结果与标准云对比Fig.3 Comparison of the evaluation results and standard cloud

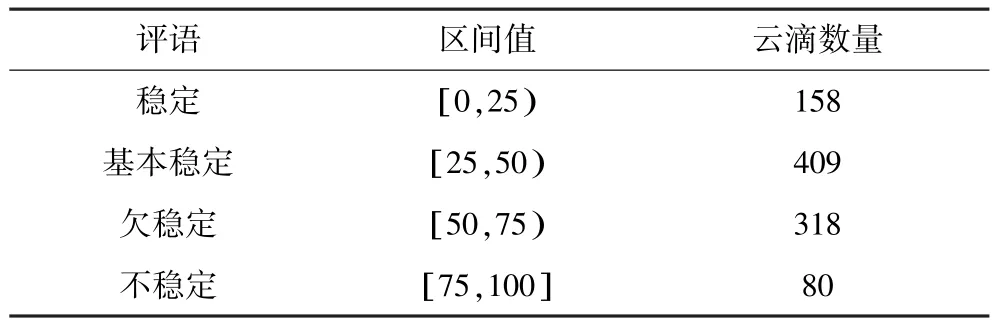
表8 小窑采空区各稳定区域中的云滴数量Table 8 The number of cloud droplet in each stable area of mined-out area of small kiln

同理,可求得渑栾高速采空区其他工作面的云模型数字特征以及稳定性级别,见表9。

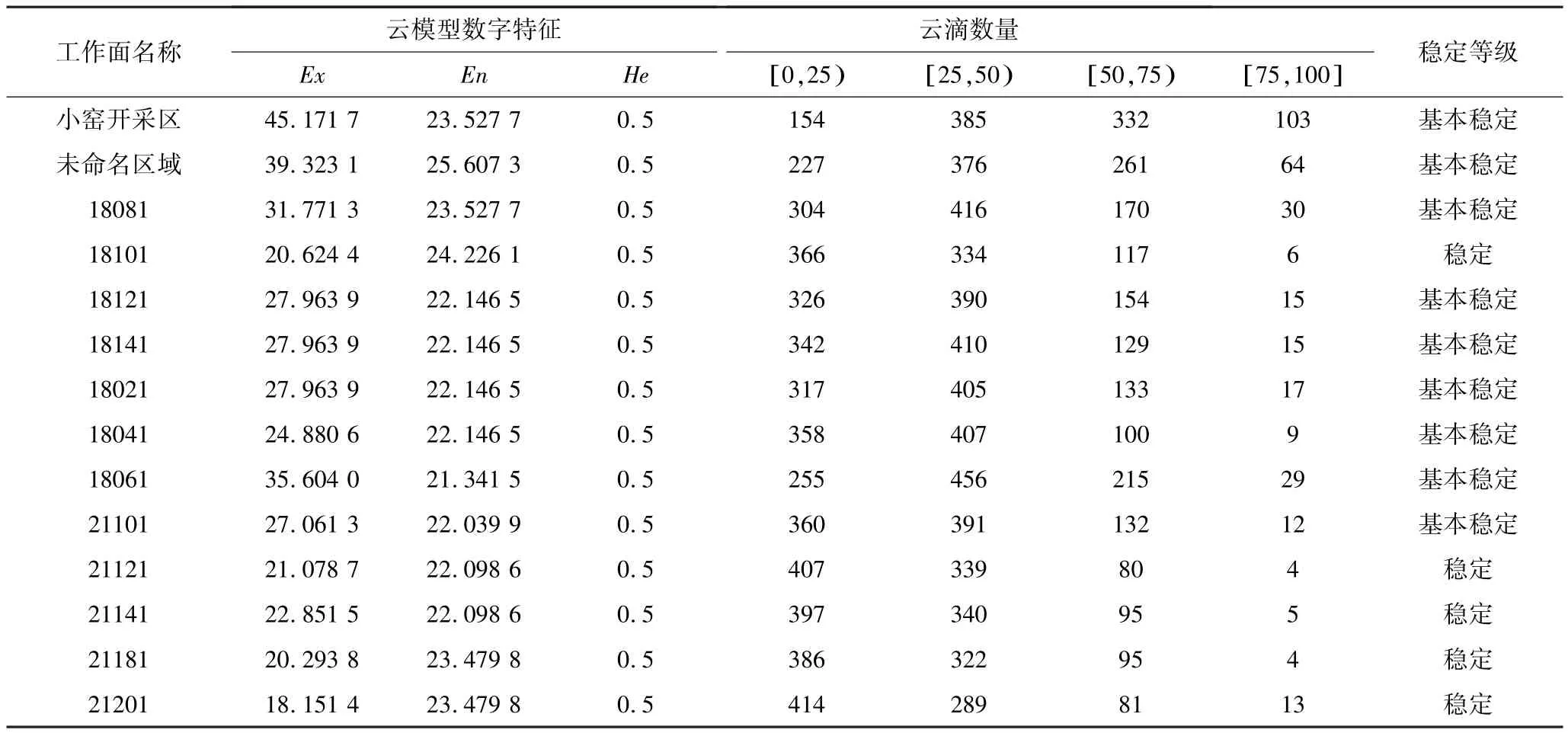
表9 渑栾采空区各工作面稳定等级Table 9 Stability levels of each working face in the Mianluan Expressway

4.4 治理对策

根据评价结果可知,渑栾高速采空区路段建设场地稳定性主要为稳定和基本稳定状态,提出在建设场地路基中加铺土工布、土工格栅等措施来提高渑栾高速的抗变形能力,如图4所示。同时在路面采用柔性材料,以满足采空区残余变形要求。

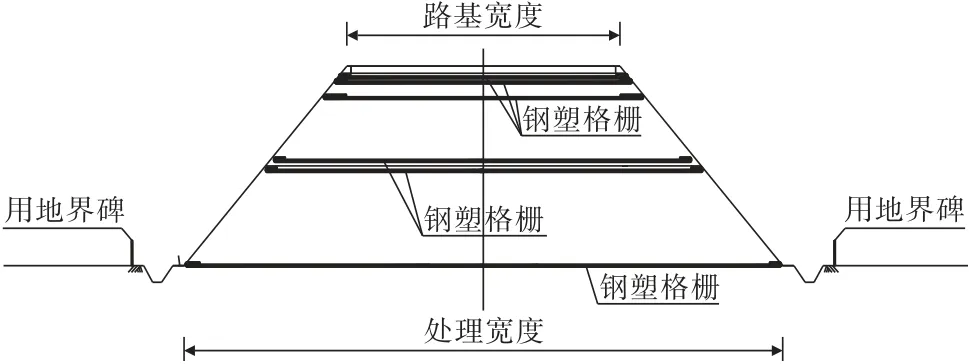
图4 路基加铺土工格栅示意Fig.4 Schematic of geogrid reinforced subgrade

5 结 论

基于三角模糊层次分析法和云模型理论,对采空区上方建设场地稳定性进行了分析,并将研究成果应用于渑栾高速采空区路段建设场地的稳定性评价,得出以下结论:

(1)从水文地质条件、开采技术条件、场地变形特征和外界扰动4个方面构建了采空区建设场地稳定性综合评价体系。该体系涵盖了12个评价指标,有助于克服建设场地稳定性评价指标的模糊性、随机性不足,能准确、全面地评价煤矿采空区建设场地的稳定性。

(2)采用三角模糊层次分析法,构建了满足一致性的三角模糊判断矩阵,通过对判断矩阵的模糊化处理,有效避免了专家个人评价偏好或偏坏程度过高对指标权重确定的影响,最终计算得出准则层的水文地质条件、开采技术条件、场地变形特征和外界扰动4个方面的权重分别为0.200 2、0.313 6、0.256 4和0.229 8。

(3)依据云模型理论,将影响渑栾高速采空区路段建设场地各评价指标的评语集转换为云模型的3个数字特征,通过落在每个区域内的云滴数量可判断出每个工作面的稳定性级别,实现了定性概念转换为定量信息,在一定程度上淡化了主观因素的影响,使得建设场地的稳定性评价结果更加科学合理。

(4)根据研究结果判断出渑栾高速采空区路段建设场地各工作面的稳定性级别主要为稳定和基本稳定,并据此提出了在建设场地路基中加铺土工布、土工格栅等措施来提高渑栾高速的抗变形能力,确保其运营安全。