含软弱夹层顺层岩质边坡锚固优化分析
郭献章 杨治华 李凤柱 张娟霞 郑立志 张学芝
(1.东北大学秦皇岛分校实验教育中心,河北 秦皇岛 066004;2.北方燕盛工程技术有限公司,河北 秦皇岛 066000;3.东北大学秦皇岛分校资源与材料学院,河北 秦皇岛 066004;4.东北大学秦皇岛分校发展规划处,河北 秦皇岛 066004)
含软弱夹层岩质边坡的稳定性分析及其失稳后 的加固研究,历来受到研究者的重视。基岩顺层滑坡在各类滑坡中占比最高,以长江三峡库区为例,基岩顺层滑坡占滑坡总数的62.0%,据对库区干流库岸283处崩塌滑坡发生的地层层位和岩性的统计结果,约有90%的崩滑发生在含有软弱面或软弱层(带)的层状岩层中[1-2]。基岩顺层滑坡在我国普遍存在,易发生于层理发育的沉积岩地层边坡,成永刚等[3-4]对国内81处顺层岩质滑坡研究后发现,层面倾角为10°~25°时,对顺层岩质滑坡贡献程度最高。
在国外,早期以极限平衡理论为基础,发展了多种边坡评价的理论,近期随着信息与计算机技术的发展,基于有限元和有限差分法的多种关于边坡的理论与软件技术逐渐成熟与发展起来。在我国,随着矿业工程和众多大型水利水电工程的成功建设,有关边坡的工程理论、实践与各种施工规范也迅速发展并成熟应用。
国内外对于顺层滑坡及其加固的研究日趋增多。如引入了时空区域的概念模拟降雨引发顺层滑坡[5],运用了岩石分级、边坡分级、连续边坡质量分级等方法,利用地理信息系统进行稳定性分析,研究大降水与露天开采协同引发滑坡的机制[6],应用大型剪切实验机对软弱夹层的力学行为进行现场原位实验[7],利用离心机原理模拟含倾斜软弱夹层的边坡地震荷载响应实验[8],并推导出其法向变形的本构函数[9],基于相似理论,建立地质力学模型,以研究其变形破坏机理[10-11],用实验的方法研究尺度和临界度对顺层岩质边坡稳定性的影响[12]等,使顺层岩质边坡的加固治理有了一定的理论基础与实践经验。
在加固方案优化方面,Hojat Dehestani等[13]研究了失稳岩质边坡临界区加固单元的最优分布,提出了岩土力学加固等级(GRR)的方法,试图降低顺层边坡的加固成本以便使更多的失稳边坡得到加固。国内也有很多学者试图找出顺层边坡加固方案优化中的通用理论与通用方法,但到目前为止,收效不大,原因是这类边坡滑坡内因的多样性及其外部诱滑条件的复杂性。因此,边坡加固方案的优化还停留在“一事一议”,或“一类一议”阶段。
由于含水、易风化、强度弱化的边坡,各种强度参数处于动态变化中而难以准确取得,从而使基于强度参数的稳定性评价和支护方案难以确定。激进方案易留隐患,但过分保守的支护方案与高昂的加固费用,使得露天矿边坡的支护面积难以扩大,许多易风化边坡得不到及时的加固,只能等其风化滑塌后才不得不进行高昂的被动支护[14]。因此,在全面客观详实勘察数据的基础上,针对具体边坡进行科学合理的分析与支护方案的优化,可在提高边坡支护的经济性的同时,使边坡主动保护的面积在可负担的范围内大幅扩大,从而为露天矿边坡的长期安全提供有效的保障,仍有极大的研究与应用价值。
河北钢铁集团矿业公司司家营北区露天矿东边坡,是典型的含水易风化顺层边坡,地表标高约40 m,境界坑底约-600 m,现状东边坡已经靠帮约至-200 m。开挖及靠帮过程中,不断有小规模的断层破碎带引起的滑坡,也有历时3~5 a风化后的强度弱化所引起的滑坡,滑坡治理的费用在逐年增加。N26勘探线强风化边坡出现险情后,进行了详勘,认为部分边坡岩性为易风化岩,风化特征为顺层结构面在降水及爆破振动的作用下,矿物间的结构发生变化,以致强度弱化。如果能够尽早发现并及时封闭这部分坡面,则可以防止后继滑坡的发生。以此为背景,展开了边坡稳定性分析及滑坡治理方案的研究,把经典理论与数值模拟相结合,优化了锚固方案,减少了施工浪费,从而为边坡的大面积加固奠定了理论与方法基础。
1 工程概况及锚固优化
按照锚索加固的原理与施工工艺,锚固工程中的优化分为设计方案优化与施工工艺优化,此处特指设计方案的优化。在锚索的设计优化中,又可分为锚索参数优化与锚固参数的优化,根据难度与重要性,此处仅研究锚固参数优化,即长度优化、倾角优化、排距优化、间距优化。
司家营北区露天矿产能2 000万t/a,地质条件复杂,矿山规模大,需支护工程量大。N26勘探线强风化双台阶边坡拟采用格构梁+锚索的锚固方式,锚固参数的优化关系到边坡安全、施工难度与经济效益。按照原设计,不足 1 200 m2的边坡,就需要321.6万元的坡面加固工程费用,还不包括排水系统工程(18.22万元)和监测等费用。高昂的加固费用令矿山今后的治理工程难以为继,因此,加固参数必须优化。
为减小工作量,根据实际情况设置边界条件,使优化工作集中关注工程的要点。根据前期工作已经确定了所研究边坡的锚固角为35°,即锚索与水平面夹角为35°;锚索长度为滑移面到坡表沿锚索方向的距离再加上6m,6m被视为稳定边坡中的持力段,因此长度优化就转化为关键软弱夹层的确定。
当边坡由含软弱夹层的顺层岩体组成时,又没有明显的优势滑塌面存在,则确定极限平衡软弱夹层和规定安全系数下的软弱夹层就成为第一个锚固优化的关键因素。在没有加固的情况下,前者将成为优势滑塌面,该面之下的边坡将是稳定的,该面之上为下滑三角体;在加固后的边坡上,后者为安全系数下的分界面,该面之下的岩体将被视为具备安全储备系数。
2 关键软弱夹层的确定
2.1 利用极限平衡理论推导K S-d关系
依据边坡参数,建立如图1的计算模型,先用解析法推导出KS-d之间的关系式,并用MATLAB软件绘制KS-d曲线,再应用Geo-slope软件模拟,用以公式校核,并最终确定优势软弱夹层。
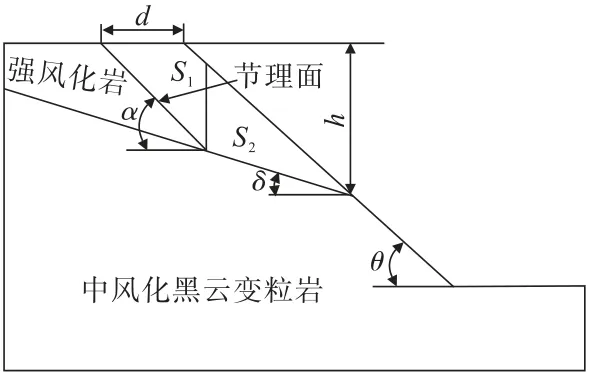
图1 计算模型Fig.1 Calculation model
根据极限平衡理论推导如下:
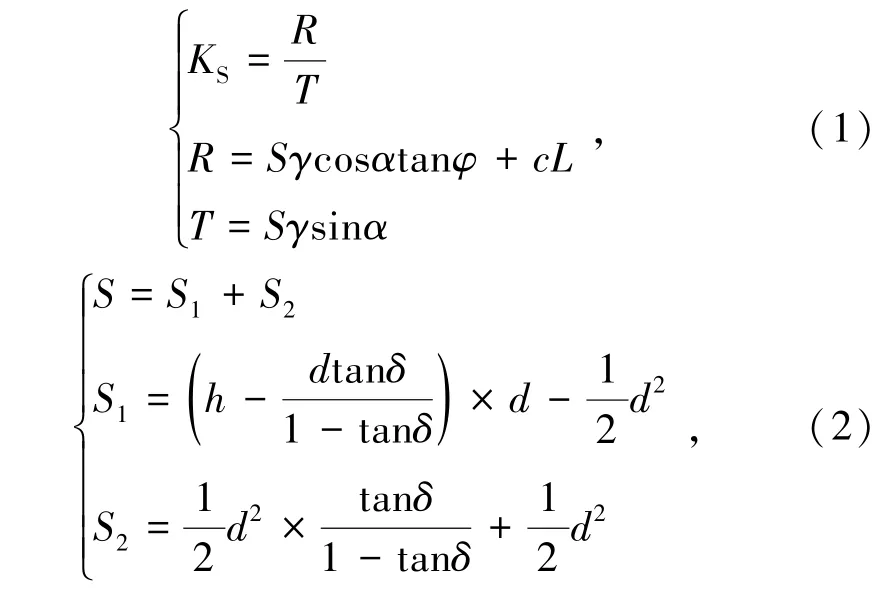
式中,KS为安全系数;T为下滑力;R为抗滑力;S为滑体面面积;L为滑动软弱夹层面长度;γ为岩体重度;α为软弱夹层倾角;φ为软弱夹层内摩擦角;c为软弱夹层黏聚力;θ为边坡倾角;d为坡肩距滑面距离;δ为强风化和中风化黑云变粒岩交界处的倾角。
此处,θ=45°,α=45°,δ=17°,h=18.4 m,其他参数如表1所示,代入上述公式,得到如图2所示的KS-d曲线。
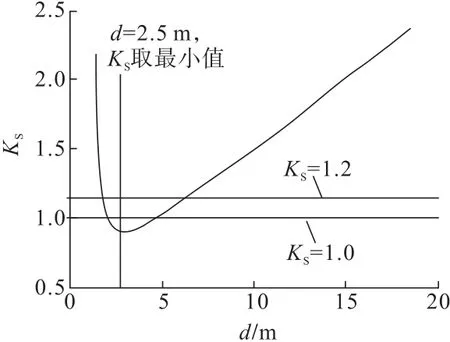
图2 KS-d曲线Fig.2 Curve of K S-d
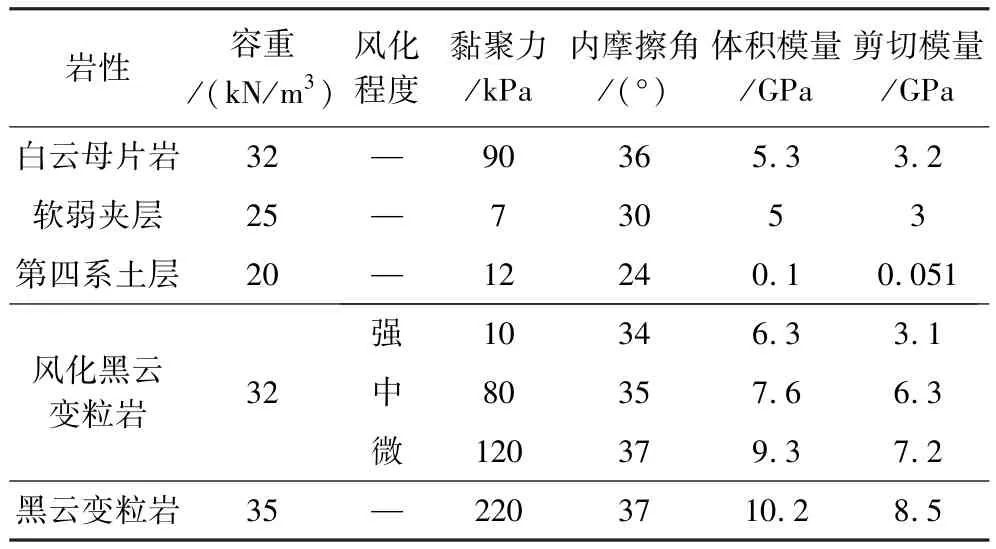
表1 边坡岩性参数值Table 1 Lithologic parameter values of slope
由图2知,安全系数KS随着d的增大先减小后增大,安全系数为1的直线与KS-d曲线有2个交点,一个大约在d=6.5m的位置,所以当d大约在6.5m时,边坡处于极限平衡。此时所对应的软弱夹层可视为极限平衡层面;另一个交点约在d=2 m处,说明此处也有一个浅表的极限平衡面,但当2 m≤d≤6.5 m时,这部分岩体处于失稳状态,因此只能把d≥6.5 m做为极限稳定岩体。同时,当KS=1.2时,也与KS-d曲线有2个交点,同理,也只把d≥7.5m的岩体看做是安全系数KS≥1.2的边坡体。
2.2 利用Geo-slope数值模拟验证K S-d曲线
FLAC3D计算安全系数是利用强度折减法,通过对材料强度属性折减弱化,找到边坡的临界破坏材料参数,最后通过比值得到安全系数,计算的结果为安全储备系数;而上述极限平衡理论所得的安全系数是利用下滑力和抗滑力的比值,计算的结果为稳定安全系数,两者得到的结果不是同一个概念。而Geoslope采用极限平衡的方法模拟,其理论基础核心也是静力平衡的原理,所以用Geo-slope非常合适与上述理论计算比较,从而验证KS-d曲线的正确性。
首先比照解析模型建立CAD模型(如图3),导入Geo-slope。赋值说明如下:节理距坡肩小于1 m时,节理间隔0.2 m(由于前5条软弱夹层太密,图中没有显示),大于1 m时,节理间隔为1 m,节理倾角45°,材料属性按照表1参数设置。
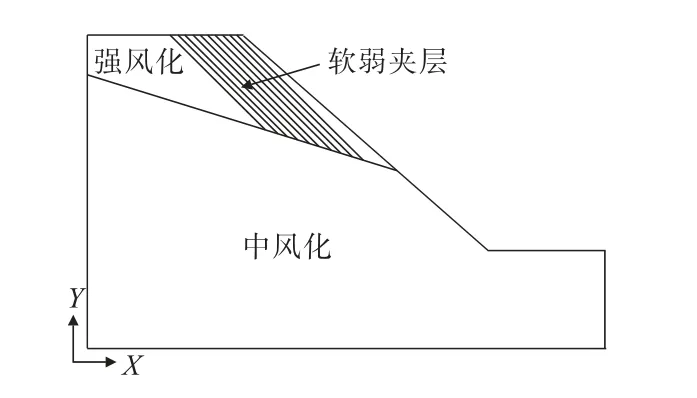
图3 Geo-slope模拟CAD模型Fig.3 CAD model for Geo-slope simulation
运用Geo-slope模拟时,从距坡肩最近的软弱夹层开始,滑移面采用完全指定的方式,从软弱夹层穿过,在强风化黑云变粒岩和中风化黑云变粒岩的交界处剪出。按照上述方式设置滑移面,从第一条软弱夹层开始模拟,记录穿过软弱夹层时的安全系数,下面以第一条软弱夹层为例分析。第一条软弱夹层计算结果如图4所示。
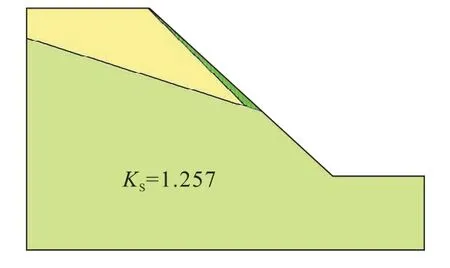
图4 第一条软弱夹层计算结果Fig.4 Calculation results of the first weak interlayer
边坡沿着设置的滑移面破坏,安全系数为1.257。此时设置滑坡体的面积比较小,软弱夹层与强风化和中风化黑云变粒岩交界处的内摩擦角和黏聚力提供的抗滑力大于滑体自重引起的下滑力,所以此时的安全系数比较大。从边坡的稳定性考虑,此时边坡比较安全,不会在此软弱夹层发生破坏。
依次改变软弱夹层做为指定滑面,模拟后得到系列的(KS,d)值。利用Origin作图软件处理后得到安全系数KS与节理距坡肩水平距离d的关系曲线图,如图5所示。
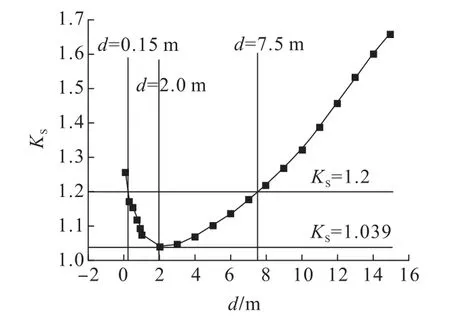
图5 Geo-slope数值模拟得到的K S-d曲线Fig.5 The K S-d curve obtained by Geo-slope numerical simulation
由图5可知:①安全系数随着滑移面距坡肩的水平距离d的增大先减小后增大;②软弱夹层大约距坡肩2 m时,安全系数最小,达到了1.039,随后呈近似直线增长,说明此时边坡在外界的扰动下首先会从2m的位置发生滑坡;而理论推导出的曲线图的最低点大致在2.5 m的位置,二者比较接近;③根据金属矿山边坡稳定性要求,永久边坡安全储备系数最少为1.2,数值模拟安全系数等于1.2时,滑移面距坡肩水平距离d大约为7.5 m(浅表位置)。如果考虑加固,虽然d小于0.15 m(浅表位置)时边坡的安全系数大于1.2,在d值介于0.15~7.5 m时,安全系数小于1.2,达不到安全储备的要求,所以取d=7.5 m,锚索长度最少为13.5 m(7.5+6 m,6 m被视为稳定边坡中的持力段长度)。
理论推导结果(图2)和数值模拟结果(图5)的KS-d曲线图对比:
(1)从趋势来说,两者都是先减小后增大,并且最终都是成直线式增长;从两者的最低点来说,理论推导公式作出的曲线图在d等于2.5 m左右时安全系数最小,数值模拟结果作出的曲线在d等于2m时出现转折点,由于数值模拟d大于1 m时取值为整数,所以安全系数最小点应该在2 m左右,两者结果类似。
(2)数值模拟最小安全系数为1.039,理论计算安全系数为0.75左右,两者有一定差距,这主要是因为理论公式中仅把强度最小的软弱夹层参数做为唯一的强度参数参与了计算,没有考虑其他岩体的参数,因此比较保守。但对于含软弱夹层的顺层边坡来说,对滑坡起决定作用的还是滑面的力学性质。从上述两方面来看,理论推导的公式更适用于单台阶节理边坡安全系数计算。
(3)两者在安全系数为KS=1.2时,都显示软弱夹层距坡肩d大约为7.5 m,两者数据吻合较好,因此锚索长度最少为13.5 m。
3 排距优化
3.1 参数选择及依据
所研究边坡由薄片状顺层黑云变粒岩组成,过密的锚孔排距、间距会破坏岩体的完整性,过大的排(间)距,又会使层面因受力不均而破裂,所以设计和施工单位加固方案已经确定锚孔间距为6 m,排距可在 4、5、6 m间选择优化。为了防止滑体从岩体强度风化严重的坡脚处剪出,在中风化黑云变粒岩处加密锚索,设置水平间距从6 m变为5 m,并伸入微风化3 m,保证能够锁住滑体。
选择弱层面的法向为锚孔方向,是因为黑云变粒岩为硬岩,弱面的内摩擦角约为30°,通过法向预应力可得到较大的切向抗滑力,同时也可以有效节省锚索的长度。
基于以上条件,利用FLAC3D数值模拟软件和局部强度折减法,不考虑水的影响,仅在重力作用下计算不同间距时的安全系数,根据计算选择最优结果,作为最终的优化方案。
根据现场施工队所采用的锚索和锚索参数,确定3种方案的锚索参数,均为:直径 26 mm,型号HRB335,抗拉强度设计值300 MPa。
根据建筑边坡工程技术规范,确定岩石与锚固体粘结强度标准值(如表2)。

表2 岩石与锚固体极限粘结强度标准值Table 2 Standard values of ultimate bond strength between rock and anchor solid
注浆浆液参数:水泥的粘结强度标准值为1×105Pa,单位长度水泥浆刚度1×109Pa,根据工程施工现场实际,注浆体的直径选100 mm。
3.2 数值模拟结果
图6分别是排距为4、5、6m时的FLAC3D模拟结果,安全系数分别为 1.35、1.34、1.32。

图6 FALC3D模拟锚索剪应变增量和轴力云图Fig.6 Cloud diagram of rock anchor cable shear strain increment and axial force by FALC3D simulation
图7为安全系数—排距关系拟合曲线,排距为4、5、6 m时的FLAC3D安全系数分别为1.35、1.34、1.32,安全系数随排距的变大而减小。排距为6 m时,边坡安全系数为1.32,满足永久边坡安全系数储备要求,同时根据甲方及施工队的要求,确定垂向上锚孔排距6 m为最优值。
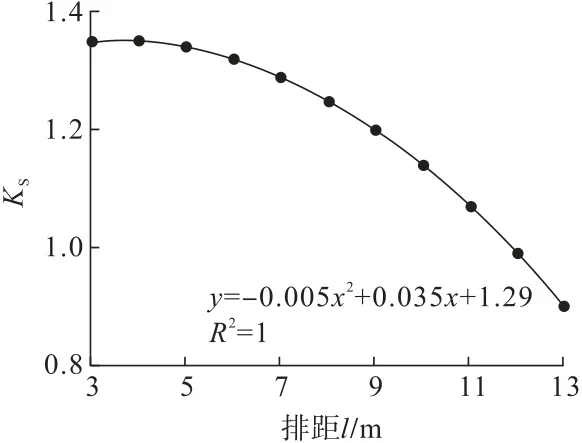
图7 安全系数—排距关系拟合曲线Fig.7 Fitting curve of safety factor-row spacing relationship
各排锚索参数具体数据如表3所示。
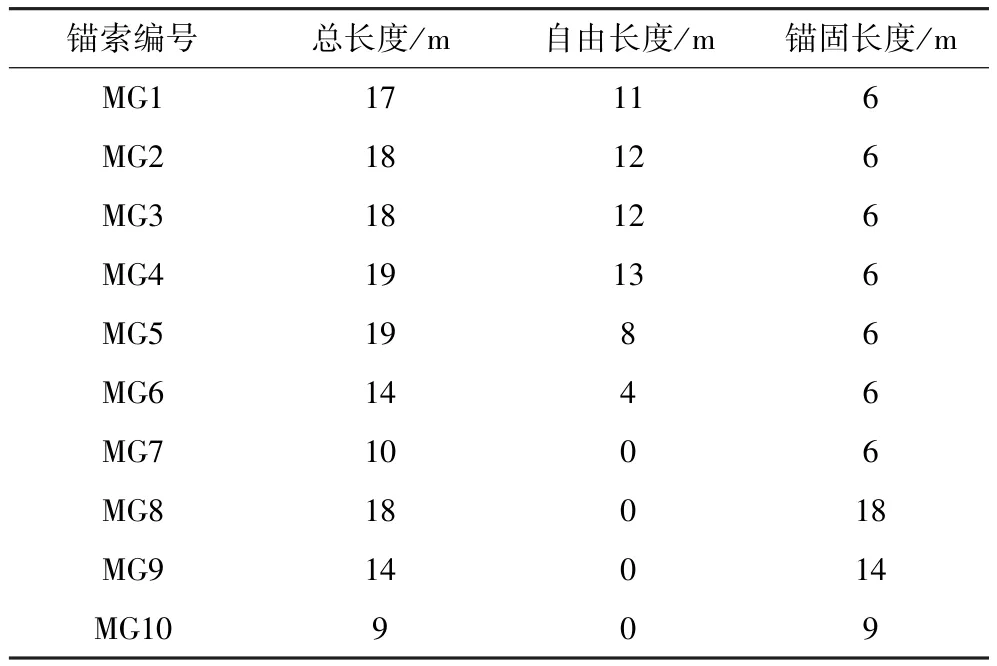
表3 锚索参数Table 3 Anchor cable parameters
排距选择6 m时,最优锚固模型如图8所示。
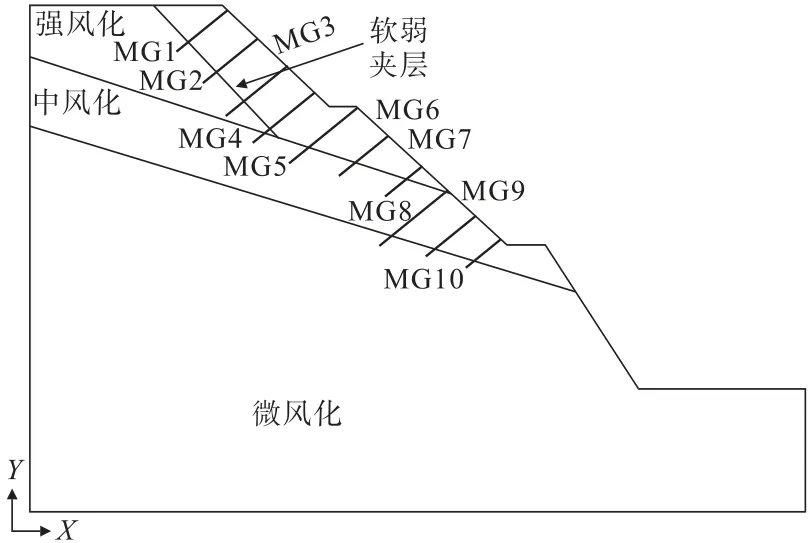
图8 最优锚固模型Fig.8 The optimal anchoring model
3.3 对最优模型的数值模拟
在自身重力和静水压力影响下对排距为6 m锚固模型模拟分析,结果如图9所示。
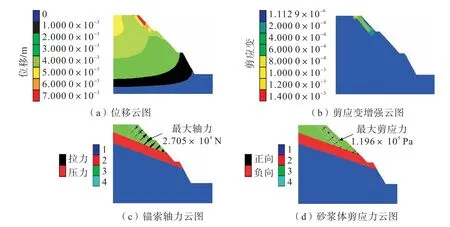
图9 最优锚固模型的FLAC3D模拟结果云图Fig.9 FLAC3D simulation results of the optimal anchoring model
从图9(a)可以看出,最大位移出现在坡面位置。从图9(b)来看,最大剪应变增量出现在节理位置,但没有从边坡剪出,说明此时边坡较稳定。从图9(c)可以看出,由于边坡内部沿软弱夹层错动,软弱夹层受到挤压,导致软弱夹层位置锚索受压。在强风化和中风化交界面以内,锚索受压,由于在锚索末端深处部分滑体有从-67 m台阶坡脚处剪出的趋势,导致一部分岩体受压。最大轴力为27.05 kN,根据锚固段长度设计公式(3),计算得到2 m≤la≤6 m,所以锚固长度6 m足够。
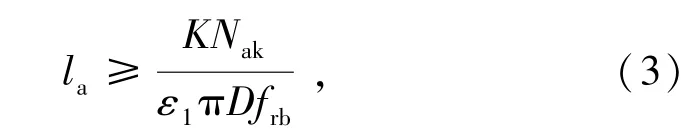
式中,la为锚固段长度;K为锚索锚固体抗拉拔安全系数,此时取2.6;Nak为锚索轴力;D为锚固体直径;frb为地层与锚固体粘结强度的特征值;ε1为锚索与地层粘结工作条件系数,永久边坡取1.0,临时1.33,此处取ε1为1.0。
比较图9(c)与图6的最大轴力可知,2种滑坡模式对所引发的滑坡体厚度相差很大。在有水介入时,因无明显的优势面,所以先使浅部软弱夹层的内聚力与内摩擦角急骤下降而引发浅层滑坡;而无地下水介入时,软弱夹层的弱化缓慢且深、浅部位相差不明显,一旦滑坡,往往是某深层滑移面抗滑力小于下滑力而引发。因此滑坡体对锚索施加的轴力会因滑坡体厚度不同而相差很大。以上特点表现在本文所研究的岩质顺层露天边坡上,是雨后常发生一些滑坡,但基本上是浅层滑坡;而深层大规模的滑坡,往往与先前贯通的优势裂纹相关,雨水的进入有促滑作用,但决定性因素却是原有优势软弱面。
4 优化成果
复杂的含软弱夹层的顺层边坡,如果各岩层间的风化速度不一致,易受爆破振动和地下水的影响,使边坡的稳定性评价复杂化、动态化[15],对达不到安全要求的边坡,在加固方案的制定时,就必须“因地制宜”,充分考虑边坡的“共性与个性”,优化加固参数,找出经济合理的治理方案。
按照原设计加固方案,-18~-42 m台阶边坡原设计加固5排,锚索总长度为72 m;优化设计为加固总共4排,锚索总长度为72 m,工程量没有变化,但锚固受力得到了优化,为以下台阶的优化创造了条件。-42~-67 m台阶原设计加固7排,总长度为126 m;优化为加固总共6排,总长度为83 m,比原设计少加固43 m,减少长度占总长度1/3,且受力更加合理,边坡安全得到了保障。
以此优化方案为模板,对整个边坡上有潜在滑塌危险或已经出现滑坡的10多处边坡的加固设计方案进行了优化,优化后的工程安全系数不变,但受力更加合理,工程量比原设计方案总体减少了1/4以上,经济效益显著。
5 结 论
根据工程实例的具体要求,在施工现场、施工队伍确定后,以项目设备及施工条件的制约为优化的边界条件,对含软弱夹层的顺层岩质边坡锚固方案进行了优化,主要优化环节为通过KS-d曲线、KS-l曲线的确定,得到d与l的最优值,并建立最优加固模型,再通过数值模拟结果中水泥沙浆体的切应力正负分界面的分析,以校核此时边坡的安全性。得到结论与有益启示如下:
(1)确定关键软弱夹层到坡肩的距离d与边坡安全系数KS之间可靠的关系曲线(KS-d)是本案例的第一优化环节,只有确定了符合安全要求的关键软弱夹层,才能确定锚固的持力段,才能确定出锚索的长度。通过解析法与数值模拟法得到2个KS-d关系曲线,其形状相同,但具体数值有所差距。本例在安全系数KS=1.2时,解析法和模拟均得到滑移面距坡肩水平距离d≈7.5 m。根据现场踏勘,判断该边坡段沿软弱夹层滑塌,与解析法结果吻合,由此优化出最小锚索长度为13.5 m。
(2)应用FLAC3D通过数值模拟得到KS-l关系曲线,当排距为6 m时,边坡安全系数为1.32,满足永久边坡安全储备要求。取l=6 m,从而确定了最优模型。
(3)通过有针对性的优化,使锚固方案与原设计相比,力学上更优,工程量大减,经济可靠,总加固的锚索长度减少了1/3,为整体边坡加固奠定了理论与模式基础。

