三维动静组合加载下石灰岩力学特性研究

余永强 余雳伟 范利丹 徐 峰 周桂杰

(1.河南理工大学土木工程学院,河南 焦作 454003;2.河南省地下空间开发及诱发灾变防治国际联合实验室 河南 焦作 454003)

近些年,浅部矿产资源随着开采强度的增加而日渐枯竭,为缓解资源接替紧张的局面,深部资源的开发已提上日程。深部煤矿的采掘工作一般采用爆破和大型机器,加上深部岩体破裂程度加剧[1]和“三高一扰动”的恶劣环境影响[2],使得巷道围岩遭受较为频繁的爆破冲击、机械扰动以及地震地质作用,甚至对围岩松动圈造成了影响[3]。静载和动载的共同作用,使围岩体的强度有所下降,围岩变形难以得到有效控制,增加了支护难度且提高了支护成本。因此,利用改进的霍普金森压杆动静组合加载装置(SHPB)研究石灰岩在冲击荷载下的力学性能和破坏形式,为煤矿巷道掘进和支护提供理论参考,具有重要的现实意义。

近年来,国内外相关学者通过分离式霍普金森压杆系统(Split Hopkinson Pressure Bar,SHPB)对岩石类材料在动静组合加载下的动态力学性能进行了深入研究。金解放等[4-7]利用改进的霍普金森压杆动静组合加载装置对长径比为1.0的砂岩进行了一系列动静组合加载循环冲击试验,研究表明:砂岩单位体积吸收能随着循环冲击次数的增加而增大,以致岩石内部损伤逐渐加剧,强度明显下降。王志亮等[8]利用改进的分离式霍普金森压杆装置,选取4种不同入射波的应力幅值对黑云母花岗岩进行循环冲击,分析了冲击次数对其峰值应力、平均应变率、峰值应变和损伤值的影响。田诺成等[9]对花岗岩进行了不同轴压的等幅循环冲击,进行同等荷载的循环冲击时,总循环冲击次数随轴压增加呈先升后降趋势,即轴压使得循环冲击荷载作用下岩石的动力学特性呈先强化后劣化趋势,且轴压为60 MPa时达到循环冲击次数峰值。朱晶晶等[10]基于动态统计损伤模型,利用大直径霍普金森试验装置对花岗岩进行单轴循环冲击,通过计算累计损伤,以分析其力学性能和吸能规律。金解放等[11]、宫凤强等[12]、余洋等[13]分别利用改进的霍普金森动静组合加载试验装置,对砂岩进行了一系列循环冲击试验。研究表明:围压的施加减缓了岩石内部裂纹的发展,强化了岩石的承载能力,轴压的作用则刚好相反。LI等[14]利用直径75mm的霍普金森压杆对花岗岩在无轴压和无围压情况下进行循环冲击试验,分析了岩石单位体积吸收能与破碎块度的关系。研究表明:当动态荷载应力较低(即不超过岩石静态强度的60%)时,循环冲击基本不会对岩石造成损伤。

目前,对于岩石在动静组合加载下的力学性能、破坏形态和能量耗散虽有一定的研究,但是有关岩石在三维动静组合加载下不同围压、轴压与冲击速度对力学特性影响的分析涉及较少。本研究以石灰岩为例,开展三维动静组合加载试验,通过SHPB试验得到石灰岩的动态力学性能,分析石灰岩的应力、应变、能量损耗和破坏形态等,为研究巷道岩体在爆炸冲击荷载下的动态力学性能提供思路,研究结果对于矿山安全、高效开采具有一定的参考意义。

1 SHPB试验装置和试样

1.1 岩石试样制备

岩石试样取自中泰矿业35采区回风下山-500 m巷道中完整性和均质性均较好的石灰岩,其静载物理力学性能参数见表1。将其加工成直径为50 mm、长度为25mm,即长径比为0.5的圆柱体试件。对试件研磨,保证试件表面光滑,两底面不平整度和不平行度均要小于0.02 mm,垂直偏差满足规程要求,如图1所示。

表1 石灰岩静载物理力学性能参数Table 1 Physical and mechanical property parameters of limestone under static loading

图1 动静加载试验石灰岩试件Fig.1 Limestone specimen for dynamic and static loading test

1.2 SHPB试验装置

本研究采用河南理工大学冲击实验室改进的分离式霍普金森压杆试验装置(SHPB装置)对石灰岩试件进行冲击试验,如图2所示。SHPB装置由压杆系统、轴压系统、围压系统和数据采集系统组成,该系统可实现岩石轴向静压0～100 kN、围压 0～20 MPa和冲击气压0～2 MPa同时加载,石灰岩试件放置位置如图3所示。压杆系统包括子弹、入射杆、透射杆和缓冲杆4个部分;动力系统采用液压氮气,通过调节气压控制器改变子弹冲击速度,激光测速仪采集子弹速度。子弹、入射杆、透射杆均为钢杆,直径分别为37、50、50 mm,长度分别为400、2 400、1 200 mm,入射杆和透射杆均为变截面锥形杆,变截面段长为170 mm,小端面直径为37 mm,缓冲杆为铝杆,直径为37 mm、长度为1 000mm,相对钢杆有3倍的应变信号提升。其中钢杆波速为5.19 km/s,密度为7 800 kg/m3,弹性模量为210 GPa。

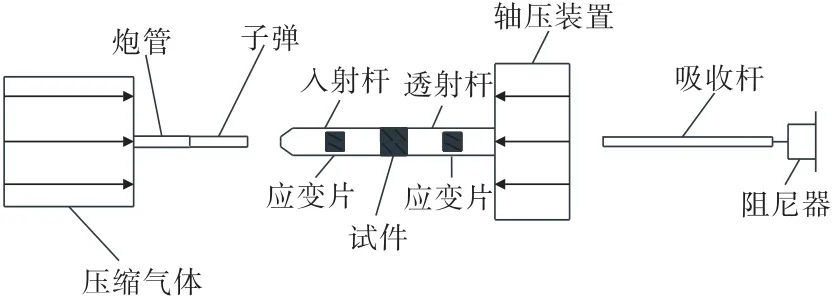
图2 SHPB系统试验装置Fig.2 Test device of SHPB system

图3 石灰岩试件放置位置Fig.3 Placement location of limestone specimen

在试验中,选取了具有代表性石灰岩试件两端的应力—时间曲线进行分析,如图4所示。由图4可知:入射波和反射波叠加后得到的应变—时间曲线和透射波的应变—时间曲线基本吻合,由此可以说明在整个试验加载过程中试件左右两端的受力是几乎相等的,从而满足了应力平衡条件[15]。

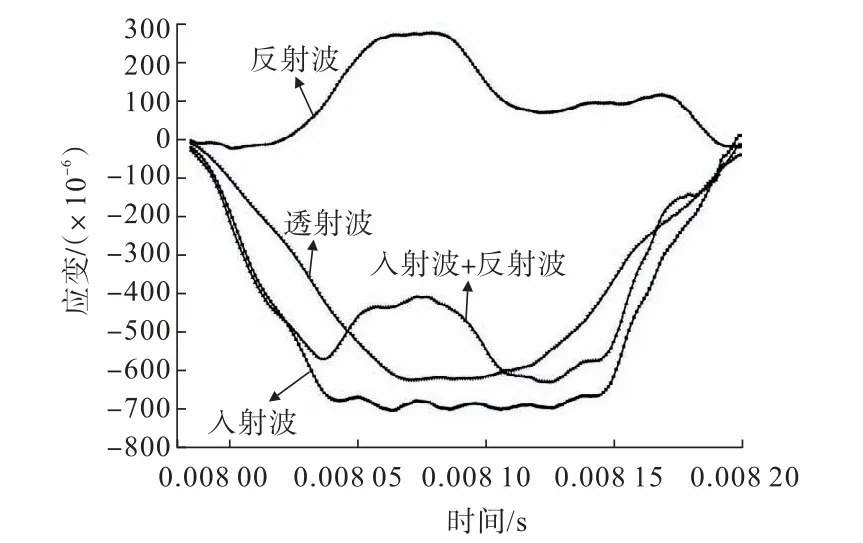
图4 石灰岩动态应力平衡检验Fig.4 Calibration of dynamic stress balance of limestone

1.3 试验原理

在液压氮气作用下,通过调整气压控制器让子弹获得一定速度撞击入射杆端部,在入射杆内产生的一维应力波向透射杆方向传递,到达入射杆与试件的接触面时,由于杆件与试件波阻抗的差异,一部分应力波将反射回入射杆,另一部分应力波则透过试件进入透射杆,经过数次透射和反射后,试件两端的应力基本趋于相同。试件的力学参数可由“三波法”计算公式[16]求得:

式中,t为时间,ms;σS(t)为试件的应力,MPa;εS(t)为试件的应变,无量纲;·εS(t)为试件的应变率,s-1;A0为冲击压杆的横截面积,mm2;AS为试件的横截面积,mm2;E0为冲击压杆的弹性模量,GPa;C0为冲击压杆的纵波波速,m/s;εI,εR,εT分别为入射应变、反射应变和透射应变,均无量纲;LS为试件长度,mm。

1.4 三维动静组合SHPB冲击试验方案

深部岩石所处环境极为复杂,本研究将受到的水平和竖直地应力简化为水平应力和垂直应力,通过对试件施加轴向和环向荷载来模拟岩石实际受力状态。为研究轴压和围压对试件强度、变形、能量耗散和破坏模式的影响,结合岩石埋深,对石灰岩试件施加不同大小轴压和围压,在此基础上取不同的冲击气压进行三维动静组合冲击试验。通过对试验系统的原始波形图进行分析计算,得到峰值应力、峰值应变和平均应变率等参数,再结合石灰岩静载物理力学性能,最终确定的冲击气压大小为0.5、0.6、0.8、1.0 MPa。为了与深部岩石处于“三高一扰动”的复杂力学环境相匹配,根据巷道围岩埋深确定了垂直应力为18 MPa,水平应力为20 MPa,本研究试验轴压分别设置为 8、15、16、17 MPa,对应于石灰岩单轴抗压强度的10%、18.7%、19.9%、21.2%,围压分别设置为 1、2、3、5、7 MPa,加载方案见表2。

表2 试验加载方案Table 2 Test loading scheme MPa

2 试验结果分析

2.1 破坏形态分析

岩石三维动静组合加载下破坏形态的宏观认识及微观破坏机理的研究分析,对于煤矿巷道中岩爆的预防具有重要意义。试件典型破裂破碎形态如图5所示,其中,图5(a)、图5(b)和图5(c)具有明显的共性,即破坏面与加载方向平行,该现象表明试件发生的破坏主要为受拉破坏。另外,图5(b)发生的破坏最为明显,其在冲击过程中发生了碎裂,在拆开热塑管后,破碎块度较小,沿环向和径向均出现了裂纹。

图5 几种典型气压及围压下石灰岩试件的破碎状态Fig.5 Fracture states of limestone specimens under several typical air pressure and circumferential pressure

对比图5(a)、图5(c)和图5(d)可知,随着冲击气压的提高,平均应变率逐渐增加,试件的损伤范围由试件边缘逐渐向中心部位扩展[16],试件的破碎程度逐渐增大,由初始的较大块度向较小块度过渡,由于试验系统轴压加载的上限值为20 MPa,此时发生的破坏主要是受拉破坏;当轴压较小时,试件内部破坏并不明显且裂纹较少;而当围压较小,增加轴压时会使得试件的破坏从边缘延伸至中心最终贯穿整个试件,从而导致试件发生粉碎性破坏。该现象与实际工程中的“岩爆”现象较为相似,基本都可归因于在较大应力状态下岩体(煤体)内部裂缝逐渐延伸且数量急剧增多,从而发生拉伸和剪切的共同破坏。

图5(b)的破碎程度尤为明显,试件表面出现贯穿上下表面的裂纹,在试件端面呈现环状破裂的破坏形态,此时为压剪破坏,试件基本失去承载能力。由图5(a)和图5(b)可知:当轴压一定时,围压的施加对试件环向变形起到了约束作用,使得试件的破坏程度降低,说明增加围压会使得试件内部变得更加紧密,从而提高试件的抗压强度,裂纹的发展变得愈加困难,抑制了裂缝产生。图5(d)中试件分裂成多个块度较大体,这是因为此时试件处于三向受力状态,受到垂直于冲击荷载方向的作用力,出现了环向拉裂现象,此时的破坏形态为压剪破坏。

2.2 应力、应变、平均应变率分析

石灰岩在轴压和气压不变时,改变围压时得到的应力—应变曲线如图6所示。由图6可知:在轴压和气压相同的情况下,当围压从2 MPa增加至3 MPa和从3 MPa增加至5 MPa时的变化趋势基本一致,且变化曲线大致可分为两个阶段,即从初始值到峰值的弹性阶段和近似线性递减阶段(图6(a))。围压的增加使得试件的强度得到提升,但是当围压增加到试件出现峰值应力时,应变开始出现回弹趋势,造成这种现象的主要原因可能是由于围压的增大使得石灰岩的抗压能力得到提升,约束了试件的变形。图6(b)曲线中围压为1 MPa时的应力—应变曲线发生了异常,斜率明显大于其他两条曲线的斜率,呈现出急增急降的趋势,原因可能是在围压较小时,试件在试验过程中发生了较大程度的破碎,试验结束后拆开热塑管也验证了这一点。

图6 轴压和气压一定石灰岩的应力—应变曲线Fig.6 Stress-strain curves of limestone under certain axial pressure and air pressure

石灰岩在气压和围压一定、轴压变化时的应力—应变曲线如图7所示。由图7可知:在同一围压下,随着轴压的增大,试件应力—应变曲线的变化趋势在整体上趋于一致性。图7(a)中的轴压在8～18 MPa区间和图7(b)中轴压在10～18 MPa区间,应变均出现了回弹现象。应力—应变曲线大致可以分为3个阶段,其中第1阶段的弹性阶段,从开始加载到峰值点,应力呈现近似一次增长,之后进入平缓阶段,此时应力无显著变化,试件内部的裂纹不断积累和发育,而应变还在持续增加,最后裂纹贯穿整个试件,内部损伤变大,试件出现屈服并发生破坏。此现象说明轴压对岩石的承载能力起到了弱化效果,也印证了文献[12]、[13]和[17]“轴压弱化岩石承载能力”这一结论。对于回弹现象,应该是由于围压的作用,使得试件原本在轴压的作用下趋于破坏,但围压对试件产生了环向的约束作用,抑制了试件的破坏。

图7 气压和围压一定石灰岩的应力—应变曲线Fig.7 Stress-strain curves of limestone under certain air pressure and confining pressure

石灰岩在三维动静组合加载下的应力—应变曲线如图8所示。

图8 轴压和围压一定石灰岩的应力—应变曲线Fig.8 Stress-strain curves of limestone under certain axial pressure and confining pressure

由图8可知:当冲击气压逐渐增加时,试件的强度、应力及应变值均会增加,应力的增加会使得试件的弹性模量增加,说明试件的刚性增强。试件的变形阶段大致可分为弹性阶段、裂纹发展阶段、变形阶段和屈服破坏阶段,在应变达到峰值后,出现回弹现象。在初始弹性阶段,随着应变增加,试件的应力呈现线性增加,增加到应力峰值时,试件内部微裂缝发育并持续扩展,之后出现显著的变形阶段,此时试件的强度得到微小的提升;当应力达到屈服应力以后,试件的应变微小增加,但应力下降迅速,试件完全破坏。

2.3 能量耗散分析

基于一维应力波理论[18],SHPB试验过程中入射能、反射能和透射能可分别进行如下计算:

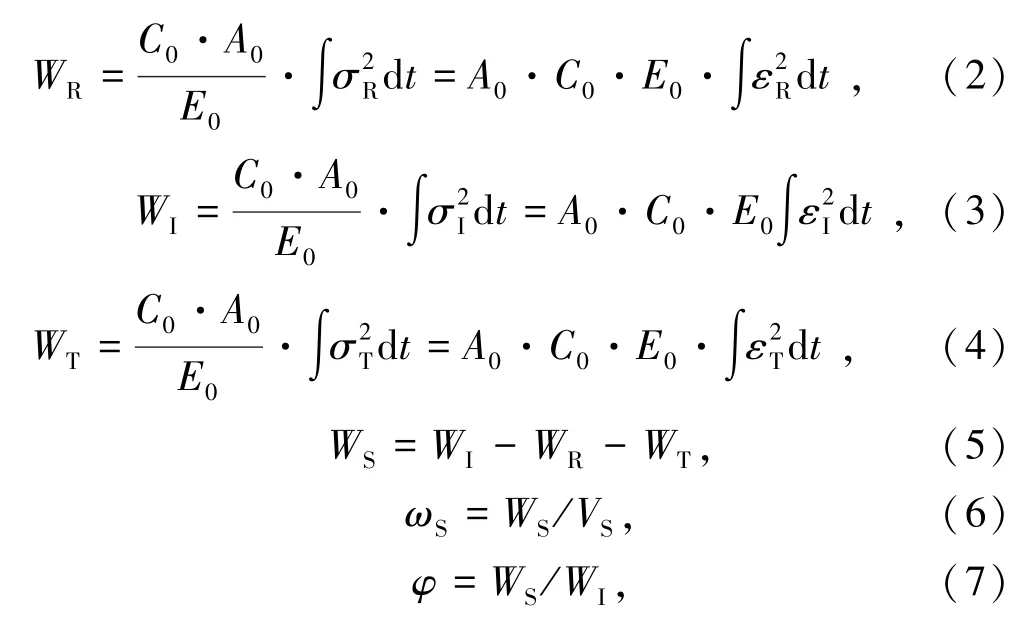
式中,WI、WR、WT、WS分别为入射能、反射能、透射能和耗散能,J;ωS为单位体积吸收能,J/cm3;VS为试件体积,cm3;φ为耗散率,无量纲;σI,σR,σT分别为入射应力、反射应力、透射应力,MPa。试验过程中在压杆和岩样接触面涂抹少量黄油作为润滑剂,以减小摩擦带来的能量损失。

根据一维应力波理论和能量守恒定律,将应力应变传感器上采集到的入射波、反射波、透射波通过计算得到三维动静组合冲击过程中的入射能、反射能、透射能、吸收能、单位体积吸收能和耗散率,试验数据如表3所示,SH-1、SH-2、SH-3、SH-4、SH-18 试件在试验过程中因仪器自身因素未采集到有效数据,因此不再展示。

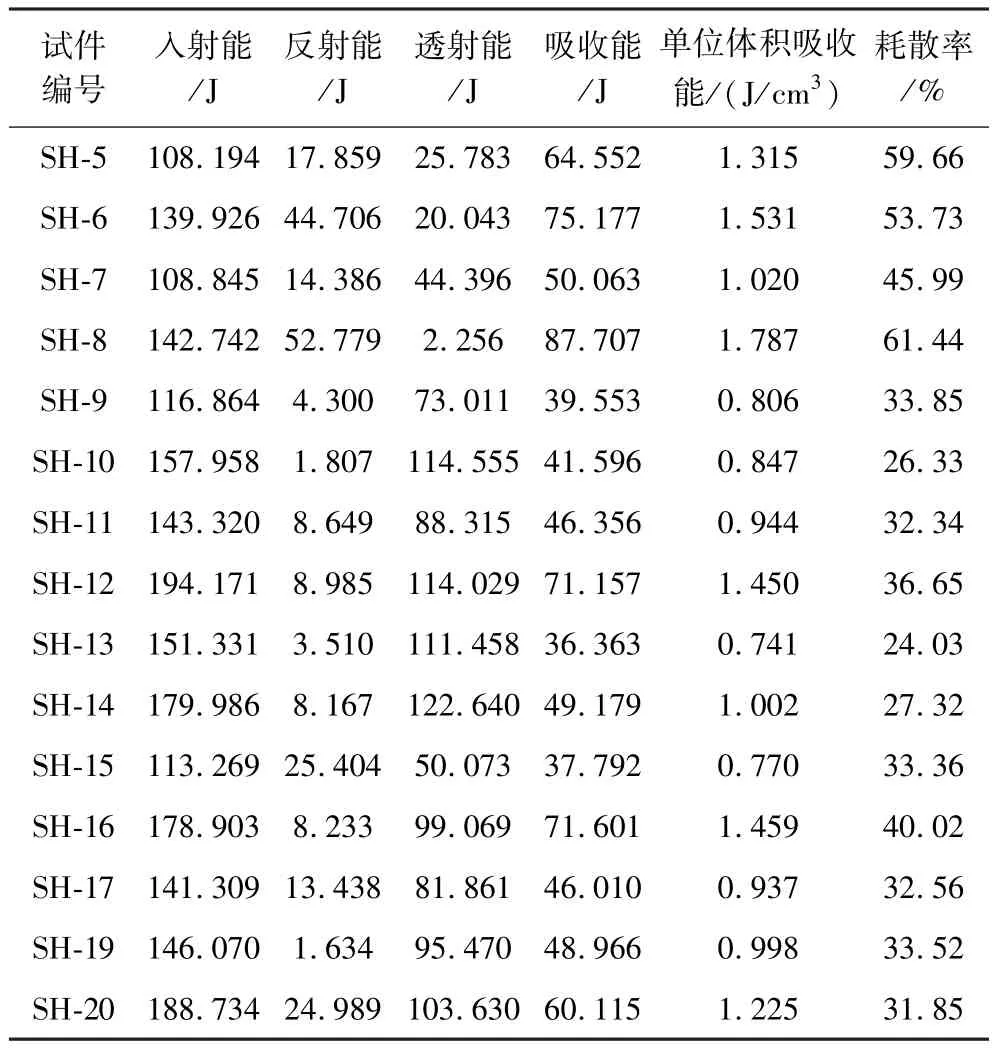
表3 石灰岩冲击能量计算结果Table 3 Calculation results for limestone impact energy

对于石灰岩冲击能量计算结果选取具有代表性的数据进行分析。将数据进行曲线拟合,得到试件在三维动静组合加载下的能量变化曲线如图9所示。由图9可知:在轴压和围压保持不变的情况下,随着冲击气压的增大,入射能、反射能、透射能和吸收能均呈现出线性增加的趋势,且吸收能大于透射能,反射能的增长趋势最为缓慢,试件变形越来越明显,在破坏形态上试件的破碎程度逐级递增。随着入射能的增加,反射能、透射能和吸收能也呈现一次函数上升的趋势,这与唐礼忠等[19]在一维静载及循环冲击共同作用下矽卡岩的力学特性试验研究结果相吻合。由图9(b)可知:随着入射能的增加,试件的吸收能也呈线性增加,吸收能占比入射能约60%,这也说明试件在三向受力状态下时,入射能有60%的能量以杆件的弹性波方式进行传递。

图9 入射能与透射能、反射能、吸收能的变化关系Fig.9 Variation of incident energy along with transmitted energy,reflected energy and absorbed energy

试件的变形和能量的传递密不可分[20],石灰岩试件在三维动静组合加载下的能量变化与其峰值应变之间的变化关系如图10所示。对试件能量的传递规律分析发现,随着峰值应变的增大,反射能、透射能和吸收能也呈现递增的趋势,但与上述分析结果有所不同,即不再是一次函数,其中吸收能增加的趋势最为显著,说明试件吸收了更多的能量用于裂纹发育与扩展,吸收能越大,试件内部缝隙越多,裂缝扩展得越广泛。从试件的破坏形态上进行解释,即试件向破坏乃至粉碎过渡,峰值应力越大,说明试件被压缩得越严重,破碎程度越严重[21]。

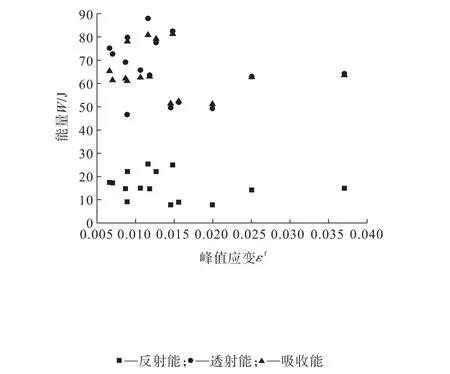
图10 透射能、反射能、吸收能与峰值应变的变化关系Fig.10 Variation of peak strain along with transmitted energy,reflected energy and absorbed energy

不同冲击气压下对石灰岩试件进行三维动静组合加载,试件的平均应变率与入射能、反射能、透射能和吸收能之间的关系如图11所示。

图11 入射能、透射能、反射能、吸收能与平均应变率关系Fig.11 Incident energy,transmitted energy,reflected energy,absorbed energy and average strain rate relationship

由图11可知:随着平均应变率的增加,入射能、反射能、透射能和吸收能与其平均应变率呈现二次函数的增长关系,这与上述反射能、透射能、吸收能和入射能之间的关系有所类似,增长速率却有所不同,入射能呈现高速增长,反射能低速增长。4个能量与平均应变率之间的线性拟合关系式为[22]

单位体积吸收能与平均应变率的关系曲线如图12所示。由图12可知:随平均应变率增加,试件的单位体积吸收能呈二次函数关系,但试件的数据点大多分布在曲线两侧左右,说明拟合曲线相关系数有所降低。在三维动静组合加载试验中,岩石试件的物理力学性质实质上是动态变化的,因而试验采用岩石试件的初态作为数据中的初值,会存在些许误差。对单位体积吸收能与平均应变率的关系图和石灰岩试件的破坏形态图进行分析发现,当试件平均应变率较低时,试件内部存在裂纹发育与持续扩展的吸收耗能;随着平均应变率增加,单位体积吸收能的增大会使得其内部呈现新的细微裂纹且持续扩展;当平均应变率较高时,在应力作用下试件裂缝相互作用、相互影响的增强使得裂缝得以交叉发展,试件沿着轴向发生劈裂拉伸破坏与压剪等破坏。

图12 单位体积吸收能与平均应变率的关系Fig.12 Relationship between absorbed energy per unit volume and average strain rate

3 结 论

基于SHPB动静组合加载试验装置,开展了三维动静组合加载下石灰岩力学特性研究,分析了不同围压、轴压与冲击速度对石灰岩力学特性的影响,主要得到如下结论:

(1)在三维动静组合加载下,当峰值应变增大,吸收能也随之增大,加速了试件内部裂缝的扩展,吸收能达到峰值时,裂纹的扩展程度达到最大,此时试件粉碎,呈现实验室“岩爆”趋势;反射能、透射能、吸收能、入射能和单位体积吸收能均随着平均应变率的增加呈二次函数增长。

(2)试件在轴压和围压不变、冲击气压变化时,应力—应变曲线可分为弹性阶段、裂纹发展阶段、变形阶段和屈服破坏阶段4个阶段,在达到应变峰值时,出现回弹现象;岩石破坏形态在不同围压下主要呈现拉伸破坏和压剪破坏,增加围压可以降低试件因受动力扰动而诱发的实验室“岩爆”概率。