以终为始:圆锥曲线问题中设线的基本原则
朱 潇
(湖北省武汉大学附属中学 430064)
笔者在文[1]中以圆锥曲线中的设线方式问题为例,分析了不同设线方式对于计算量的影响.在最近一次高三复习课“同课异构”研讨活动中,有教师提出关于设线方式的一个观点:如果直线过x轴上定点,选择“反设”(x=ty+m);如果直线过y轴上定点,选择“正设”(y=kx+b),这样就可以减少计算量.笔者认为这种观点不仅值得商榷,还固化了学生的思维,不利于数学运算素养的培养.在圆锥曲线解答题中如何选择合适的设线方式?如何将其背后的算理内化为学生的运算素养?笔者认为“以终为始”是圆锥曲线问题中设线的基本原则;在课堂上将“怎么做”扭转为“为什么这么做”,可在帮助学生理解算理的同时,让提升学生的运算素养成为可能.
1 一定要“正设”吗?
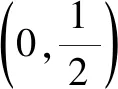
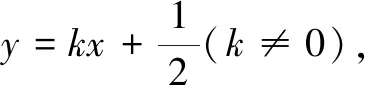
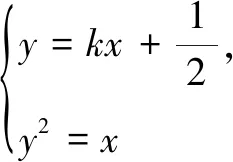

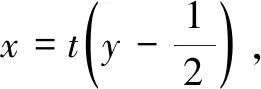

2 一定要“反设”吗?
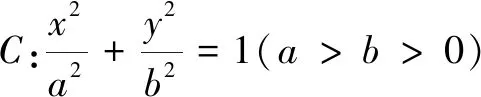
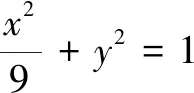
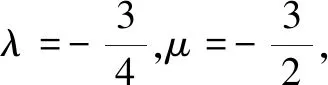
若l与x轴不重合,设l的方程为x=ty+1(t≠0),设M(x1,y1),N(x2,y2),R(0,y3).
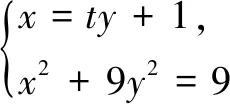

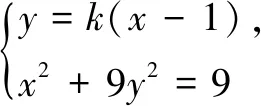


3 如何选择合适的设线方式
3.1 设线方式的本质分析

3.2 设线方式的原则
书写解题过程通常是按照设线(设点)——联立——韦达定理——翻译目标条件(结论)——利用韦达定理等步骤呈现的,而解题思维则通常需要从目标条件(结论)出发,找到其等价条件或者结论,进而寻找关于x1,x2或者y1,y2的待证式子,进而选择设线方式.这种书面呈现与思维过程的互逆性导致学生在课堂上只是被动承认过程的可行性而忽视了思维的生成性.所以设线方式选择的原则应该是“以终为始”,以题目中关键条件或者待证结论为“终”,分析解题思路之“始”,即选择合适的设线方式,并将这一思维过程在课堂中着重生成出来.下面以2021年一道高考试题加以说明.
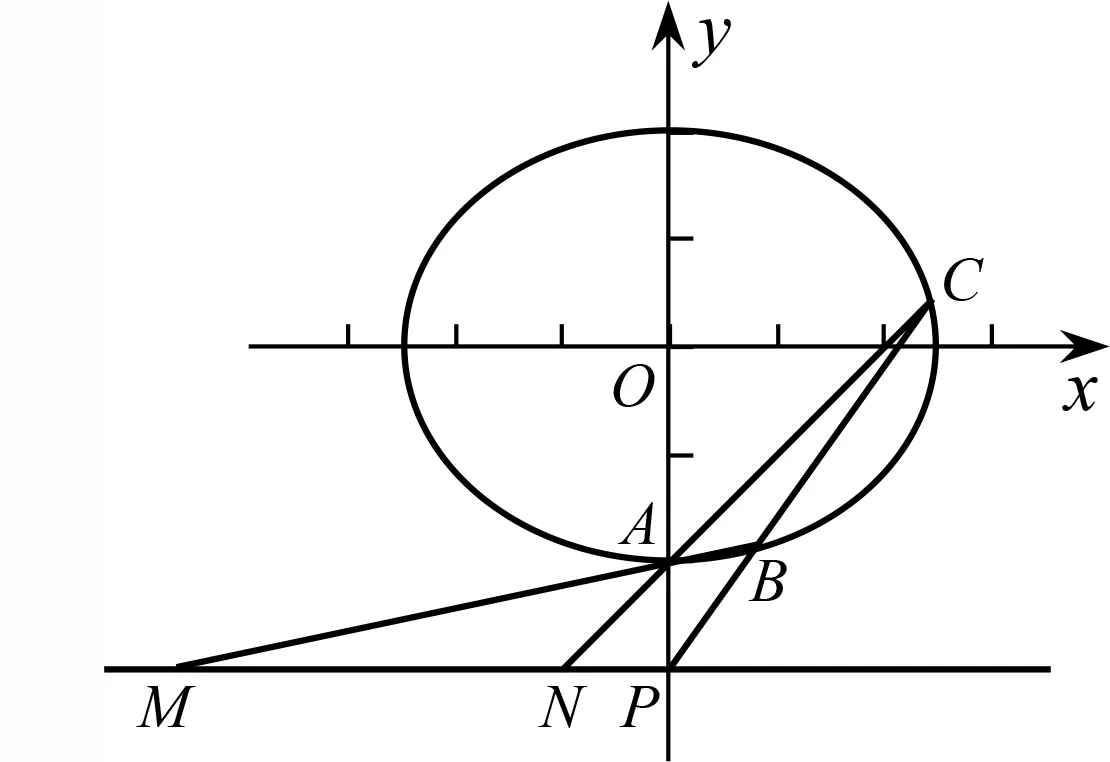
图1
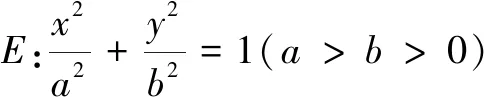

有些问题核心条件或结论的转化较为复杂,需要进行二次转化,形成新的目标式子,进而再选择设线方式.但无论是哪种类型,培养学生的目标意识,遵循“以终为始”的设线原则,进而发展用程序化的思想理解、表达问题的能力,才是数学运算素养的最终诉求.
3.3 设线方式教学的价值旨归
高三复习课的专题分类经常是题型导向,而“设线方式问题”是方法导向.《普通高中数学课程标准(实验)》中要求利用8课时左右时间专门讲《推理与证明》,内容要求结合学习过的实例讲解综合法、分析法等,体现证明数学命题的方法性[2].《普通高中数学课程标准(2017年版2020修订)》中删除了《推理与证明》,提倡将证明数学问题的方法以渗透的方式融合在平时教学内容中[3].“设线方式问题”的教学就是一个很好的载体.本专题中,在学生习得“以终为始”的设线原则的同时,教师通过带领学生分析题目关键条件(结论),以分析法的思路得到解题的起点,然后以综合法的步骤书写解题过程,将书写过程、思维过程与综合法、分析法对应,真正从“教题型”中解脱出来,进而走向“教方法”.这一过程也为发展数学运算素养提供了可行场域.
4 结语
在解题过程中目标意识是最为重要的.圆锥曲线中目标意识是“终”,设线方式是“始”.“以终为始”是解决这类目标导向很明确的问题的基本原则.长期以来,我们习惯于呈现解题方法,忽视了思维的过程.表现为教师在课堂里直接告诉学生诸如“抛物线开口向右选择反设、面积问题中水平宽为定值时选择反设”等总结好的套路,固化了学生的思维.在解题教学中遵循“以终为始”的基本原则,生成火热的思考,有助于帮助学生“知其然,知其所以然”,进而“知何由以知其所以然”.

