特殊环境下双馈风力发电机电刷磨损量建模

赵帅， 马宏忠， 程龙

(河海大学 能源与电气学院，江苏 南京 210098)

0 引 言

电刷滑环作为双馈电机静止和运动部件之间电能转换的重要部件，其本身的运行特性极其复杂，电刷损耗快，需定期更换，其工作性能极易受环境影响[1]。在复杂的海洋环境下，盐雾沉积影响电刷滑环接触面的摩擦系数，电刷的磨损量增大，电刷更换周期缩短，预测电刷的磨损量具有一定现实意义[2]。

当前国内外学者对电刷的磨损已经取得一些成果。文献[3]通过对单极发电机电刷滑环系统机械环境测试，研究了大电流密度下阳极刷和阴极刷的接触电阻，并对两极电刷不同的磨损率进行量化，发现阳极刷的磨损率是阴极刷的两倍。文献[4]从摩擦学出发，建立电刷滑环系统的磨损过程曲线，在环境变化时，会出现过渡期，并且可以观察到多个稳定磨损阶段。文献[5]通过威布尔分布的统计分析评估电刷滑环的使用寿命以及最优的定期检测方案，减少不必要的维修计划，增加了系统的可靠性。文献[6]研究了石墨碳刷与钢滑环和铜滑环之间的电压-电流特性，研究表明钢滑环的电压饱和特性与铜滑环的电压饱和特性有很大不同。文献[7]研究了电刷滑环系统中不同银含量的电刷在特定工况下的接触压降以及磨损情况，实验表明，银含量在60%～80%之间，电刷的接触压降以及磨损性能比较好，不同银含量的电刷在相同的工况下，电气磨损及机械磨损的占比有所不同。文献[8]研究了实际工况中以及实验室条件下电刷滑环系统在不同的电流密度下的磨损率，研究发现电刷滑环运行期间励磁电流在并联的电刷之间分布不均。电接触过程中摩擦模型建模也取得了一些成果，文献[9]提出一种能够准确描述运动状态下的摩擦力模型；文献[10-11]通过引进Stribeck函数建立改进的摩擦力模型；文献[12]提出了兼具静摩擦和库仑摩擦基本摩擦特性的改进的Dahl模型；文献[13-14]从波动载荷出发，研究波动载荷与滑动电接触摩擦力之间的关系，建立关于波动载荷下的滑动电接触摩擦力模型。以上研究分别研究了电刷滑环系统的磨损特性以及电接触下摩擦力建模，但未将摩擦力模型和磨损量预测结合，未涉及海洋环境下电刷磨损量预测研究。

随着双馈电机在海洋风电上的发展，针对电刷滑环系统故障诊断上取得突出成就，文献[15-17]基于振动信号提取，提出合理的滑环烧蚀故障诊断方法，但针对电刷滑环的研究仍有很多问题，如海洋环境下电刷磨损加剧更换周期难以确定等。基于文献[18]中海洋环境下盐雾对风电机组的影响以及文献[19]中对铝合金在盐雾环境中的腐蚀机理的分析，为研究海洋环境下电刷滑动电接触下的磨损量，设计了基于盐雾试验机的双馈电机电刷滑环系统磨损量研究实验平台，采用改进的库伦-粘性摩擦力模型，结合磨损理论，建立电刷的磨损量预测模型，然后，基于粒子群算法，对磨损量模型中接触电流、接触压力、盐雾浓度、运行速度以及实验温度相关的参数进行辨识，建立能够预测不同接触电流、接触压力、盐雾浓度、运行速度以及实验温度工作条件下电刷的磨损量预测模型，并利用实验数据验证该模型的可靠有效。

1 实验装置与实验方案

1.1 实验装置

图1是基于盐雾试验机的电刷滑环系统磨损试验平台，主要包括盐雾试验箱、异步电机、变频器、调压器、电网系统、电刷滑环系统以及传感器等实验设备。盐雾试验箱可以改变实验环境，通过配置1%～5%NaCl溶液，实现腐蚀环境的改变；异步电机和变频器的结合实现电刷滑环系统在0～1 500 r/min转速范围内变化；调压器可以改变电刷的加载电流，创造出不同的工况条件；传感器可以实现设备的检测和保护。

图1 基于盐雾试验机的电刷滑环系统磨损试验平台

实验中的电刷滑环系统为YKYF1500-4异步空冷双馈式风力发电机电刷滑环系统。碳刷种类繁多，可选择性较广，不同材质的碳刷磨损性能不同，选取Cu含量为10%的碳刷作为研究对象，尺寸如表1所示。

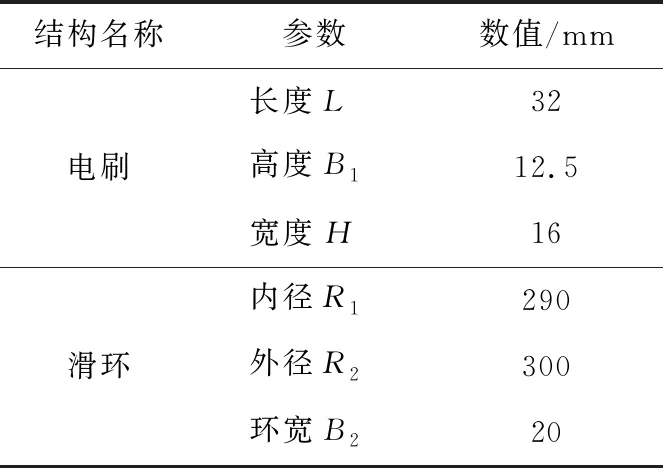
表1 电刷滑环的结构参数

1.2 实验方案

基于控制变量法，进行接触电流、接触压力、盐雾浓度、温度与滑动速度实验，共计64组实验，每组实验6 h，每组实验后用0.1 mg精确度的电子天秤测量电刷在该实验时间内的磨损量。根据电刷滑环的工况条件以及盐雾试验箱的相关实验标准，将实验条件确定为：转动速度为300、600、900、1 200 r/min；电流大小为10、20、30、40 A；压力大小为：15、20、25、30；盐雾浓度为1%、3%、5%、7%；实验环境温度为32、35、38、41 ℃。每次实验后对电刷进行冲洗、烘干和称重，减少盐雾试验箱中盐雾沉积及水汽对实验结果的影响。

图2为金相显微镜下电刷磨损前后形貌对比。由图2(a)知，磨损前的电刷表面比较光滑，磨损后，由于电刷与滑环之间滑动摩擦，电刷表面会有较明显的擦痕，另外由于盐雾沉积等腐蚀环境的影响，电刷表面会有较明显的点蚀坑，由载流腐蚀与盐雾腐蚀共同作用形成，如图2(b)所示。由以上分析可知，海洋环境下，电刷的磨损由机械磨损和电气磨损共同决定。

电刷滑环系统高速运转，滑环表面温度升高，高温环境下铜与氧气结合形成氧化膜，其反应式子如下：

(1)

(2)

一般情况下氧化膜的形成具有一定的润滑作用，减少电刷磨损。海洋环境下，暴漏在空气中的电刷滑环表面会被一层水膜覆盖，在电场作用下会被电解，游离出氢氧根离子和氢离子，即

(3)

盐雾沉积至使电刷滑环表面形成NaCl颗粒，溶于水后析出钠离子和氯离子，在水和氧的共同作用下，产生电化学腐蚀，形成腐蚀坑。其反应式子[20]如下：

(4)

(5)

由反应式子可知，海洋环境下，受环境影响，电刷工作性能改变，盐雾腐蚀造成电刷磨损加剧。

2 磨损模型的建立

2.1 摩擦力模型

1)传统库伦-粘性摩擦力模型。

随着流体力学的发展，用库伦-粘性模型来表征滑动摩擦力F(v)，该摩擦模型是由粘性模型和库伦模型结合而成，可以表示[21]为

F(v)=Fc+fvvsgn(v)。

(6)

式中：Fc为库仑摩擦力；fv为粘性摩擦系数。

库伦-粘性摩擦模型的摩擦力与速度的关系如图3所示。由图可知，摩擦力随速度增大而增大，此模型中摩擦力与速度呈简单的线性关系。实际上，摩擦力与速度之间非简单的线性关系。

图3 库伦-粘性摩擦模型

2)改进库伦-粘性摩擦力模型。

由库伦定理知，库仑摩擦力Fc与速度没有关系，对式(6)库伦-粘性模型中的粘性部分改写，即将式(6)中fvvsgn(v)改写为

Fv=σv1(eσv2|v|-1)sgn(v)。

(7)

将式(7)代入式(6)，摩擦力与相对滑动速度之间的非线性的库伦-粘性摩擦力模型[13]为

F(v)=Fc+σv1(eσv2|v|-1)sgn(v)。

(8)

式中：σv1为粘性摩擦斜率因子；σv2为粘性摩擦变化因子。从式(8)中可知摩擦力随速度非线性变化，能更好地反映滑动速度与滑动摩擦力之间的关系。

2.2 磨损量建模

根据磨损理论，用单位摩擦功的体积磨损量来衡量磨损能量与磨损量之间的关系，电刷滑环系统中电刷的磨损量可表示[22]为

M=qW。

(9)

式中：M为体积磨损量；q为能量磨损率；W为摩擦功。

式(9)表示了体积磨损量M和摩擦功W之间的关系，摩擦功可表示为

W=F(v)vt。

(10)

式中F(v)为接触摩擦力。

实验中，电刷磨损之后测量质量比较直观简洁，式(9)改写为

Ma=Mρ=ρqF(v)vt。

(11)

式中：Ma表示时间t内电刷的磨损量；ρ为材料密度。

进一步将式(11)改写为

(12)

其中Mb表示单位时间磨损量。从式(12)中可看出：电刷单位时间磨损量与物质本身的密度ρ；能量磨碎损率q；以及运行速度v和接触摩擦力F(v)相关。其中密度ρ和能量磨损率q是电刷材料的性质，通过查阅材料手册或者简易实验很容易得。速度v和接触摩擦力F(v)与电刷的具体运行工况相关，不同的工况下取值不同。将式(8)代入式(12)可得电刷的单位时间磨损量为

Mb=ρqv(Fc+σv1(eσv2|v|-1)sgn(v))。

(13)

可见，电刷单位时间磨损量由电刷的密度ρ、能量磨损率q、运行速度v、库仑摩擦力Fc、粘性摩擦斜率因子σv1、粘性摩擦变化因子σv2确定。

2.3 反映相关变量的磨损量模型

在速度为v=300、600、900、1 200 r/min，接触电流I=10、20、30、40 A，接触压力F=20 N，盐雾浓度C=5%，实验环境温度T=35 ℃的实验条件下，进行磨损量与接触电流之间的关系实验，实验结果如图4所示。随着施加在电刷上的电流的增大，电刷的磨损量先减小后增大。

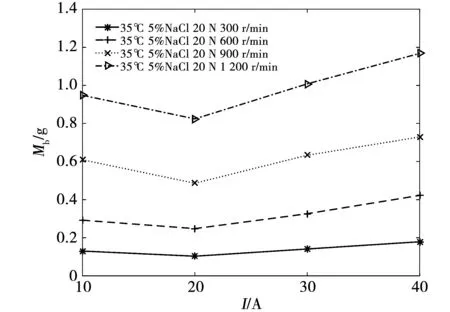
图4 磨损量与接触电流的关系

在速度为v=300、600、900、1 200 r/min，接触压力F=15、20、25、30 N，接触电流I=20 A，盐雾浓度C=5%，实验环境温度T=35 ℃的实验条件下，进行磨损量与接触压力之间的关系实验，结果如图5所示。结合磨损量的计算公式，磨损量随着接触压力的增大而增大，这与图5中的的实验结果相一致。

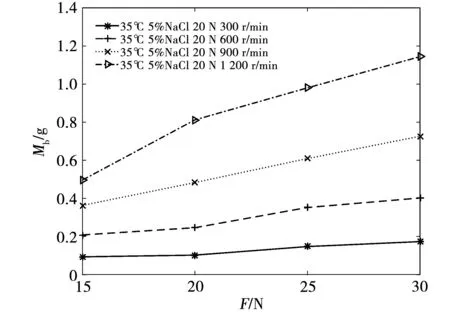
图5 磨损量与接触压力的关系

在速度为v=300、600、900、1 200 r/min，接触压力F=20 N，接触电流I=20 A，盐雾浓度C=1%、3%、5%、7%，实验环境温度T=35 ℃的实验条件下，进行试验磨损量与盐雾浓度之间的关系实验，实验结果如图6所示。环境中NaCl浓度会对碳刷的磨损量造成一定的影响，契合了海洋环境下碳刷磨损加剧的现象。

图6 磨损量与盐雾浓度的关系

在速度为v=300、600、900、1 200 r/min，接触压力F=20 N，接触电流I=20 A，盐雾浓度C=5%，实验环境温度T=32、35、38、41 ℃的实验条件下，进行试验磨损量与环境温度之间的关系实验，实验结果如图7所示。电刷滑环系统的温度比环境温度高，环境对电刷磨损性能的影响不如盐雾浓度、电流及接触压力剧烈，该曲线增长平缓。

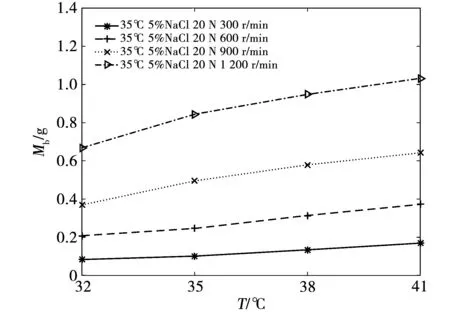
图7 磨损量与环境温度的关系

利用I、F、C、T分别表示接触电流、接触压力、盐雾浓度、环境温度，基于库伦-粘性摩擦力的磨损量模型可以改写为：

(14)

式中Mb为改进模型的单位时间磨损量。

3 磨损量模型参数辨识

3.1 粒子群参数辨识

本文采用粒子群参数辨识方法对模型中Fc、σv1、σv2进行辨识，适应度函数定义[23]为：

(15)

e[Mb,Mbi]=Mb-Mbi。

(16)

式中：e[Mb,Mbi]为第i次磨损量的预测值与实验值之间的误差；Mbi为第i次磨损量的实验值；N=4为试验次数。

当I=10、20、30、40 A，F=20 N，C=5%，T=35 ℃；F=15、20、25、30 N，I=20 A，C=5%，T=35 ℃；F=20 N，I=20 A，C=1%、3%、5%、7%，T=35 ℃；F=20 N，I=20 A，C=5%，T=32、35、38、41 ℃时，分别用粒子群算法对基于改进的库伦-粘性摩擦力的磨损量模型中的参数进行辨识。其中：参数为sizpop=60；maxgen=600；学习因子C1=2，C2=2；惯性权重ω=0.7；搜索空间维数D=3。对Fc、σv1、σv2进行最优辨识，结果如表2所示。

表2 辨识出的参数结果

3.2 磨损量模型参数辨识结果

为了确定Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)中参数I、F、C、T最高项的次数，利用MATLAB拟合工具，通过I、F、C、T分别对Fc、σv1、σv2参数进行多项式拟合，辨识结果和拟合结果如图8～图10所示。

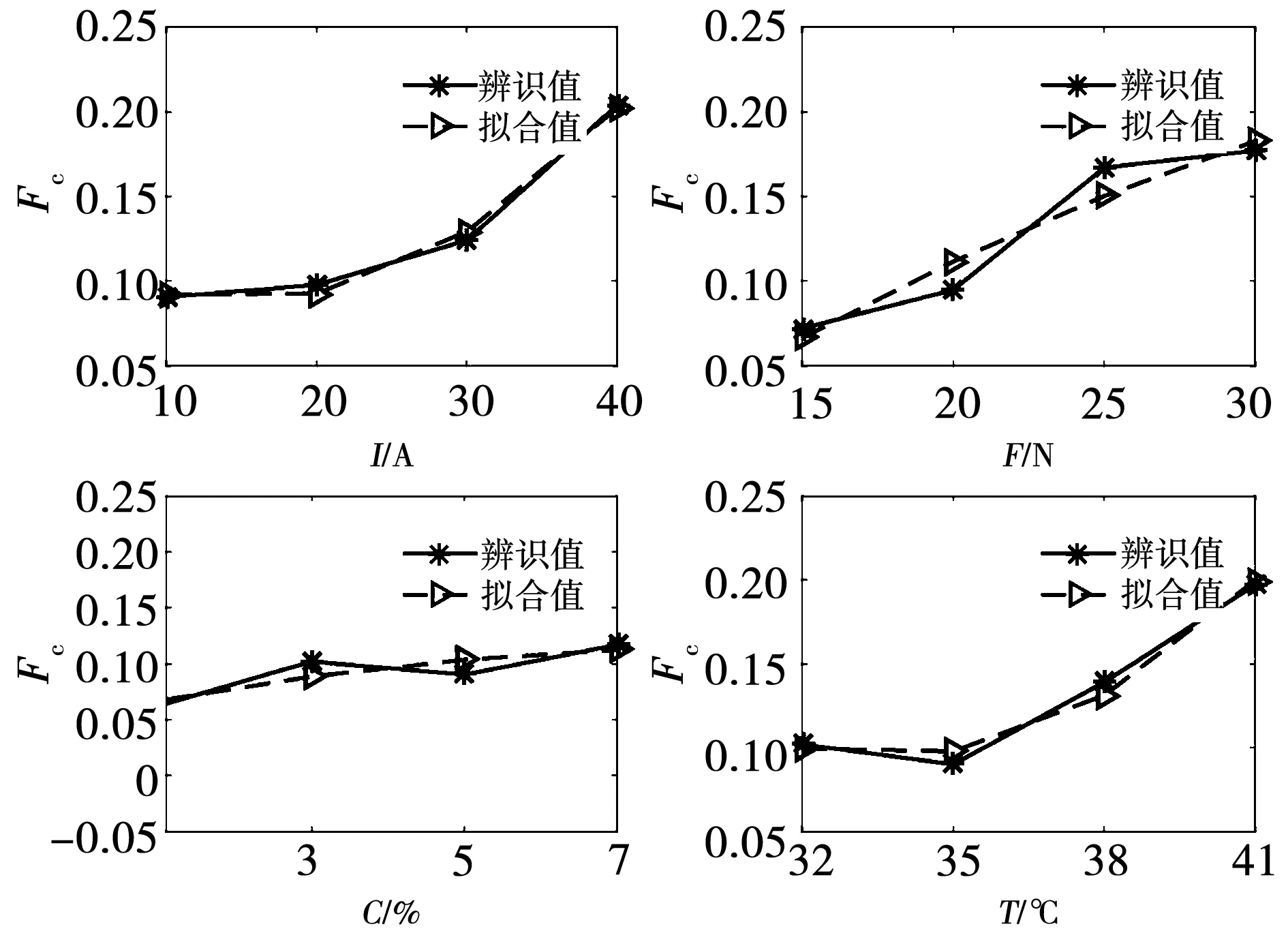
图8 Fc与I、F、C、T多项式拟合

图9 σv1与I、F、C、T多项式拟合

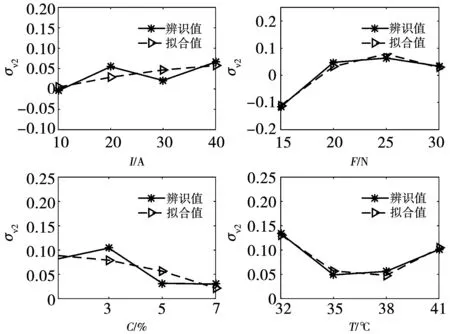
图10 σv2与I、F、C、T多项式拟合

从图可知，接触电流I与参数Fc、σv1、σv2对应二次关系关系；接触压力F与参数Fc、σv1、σv2对应二次关系关系；盐雾浓度C与参数Fc、σv1、σv2对应二次关系；环境温度T与参数Fc、σv1、σv2对应二次关系关系。因此将Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)中参数I、F、C、T最高项的次数为二次，Fc(I,F,C,T)、σv1(I,F,C,T)、σv2(I,F,C,T)可以表示为：

(17)

经过MATLAB多项式拟合，对数据进行分析后，系数如表3所示。由表4知Fc、σv1、σv23个系数的统计量，相关系数R较大，说明有较强相关性；统计量F比较大，说明通过检验可能性越大；卡方系数远小于0.05，说明通过假设检验概率为95%；残差平方和较小，说明拟合效果较好。综上所述，通过式(17)对参数Fc、σv1、σv2的多项式拟合是正确的。

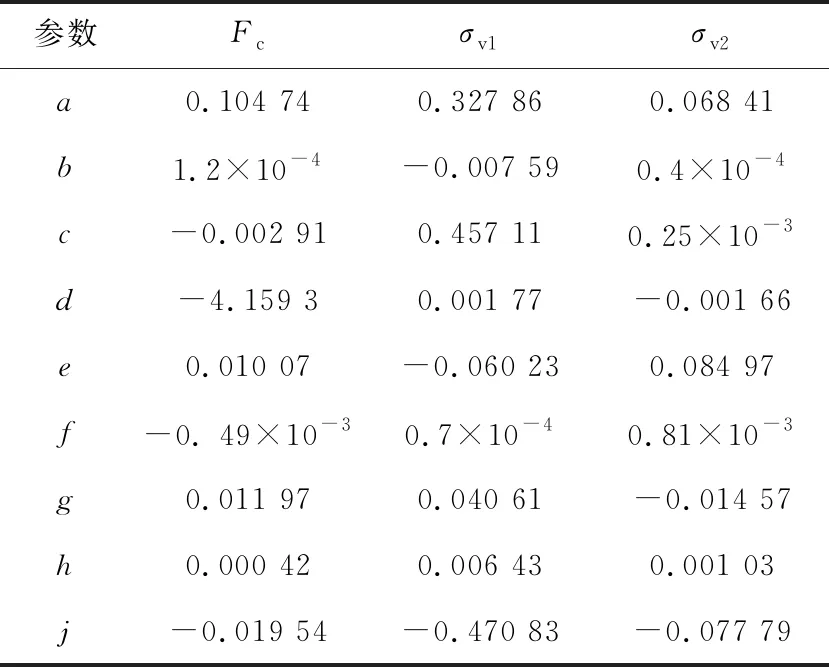
表3 参数Fc、σv1、σv2多项式拟合结果

表4 Fc、σv1、σv2的回归统计量

4 实验验证

为了验证模型的正确性，利用64组实验数据，计算出普通残差。绘制残差图如图11所示。

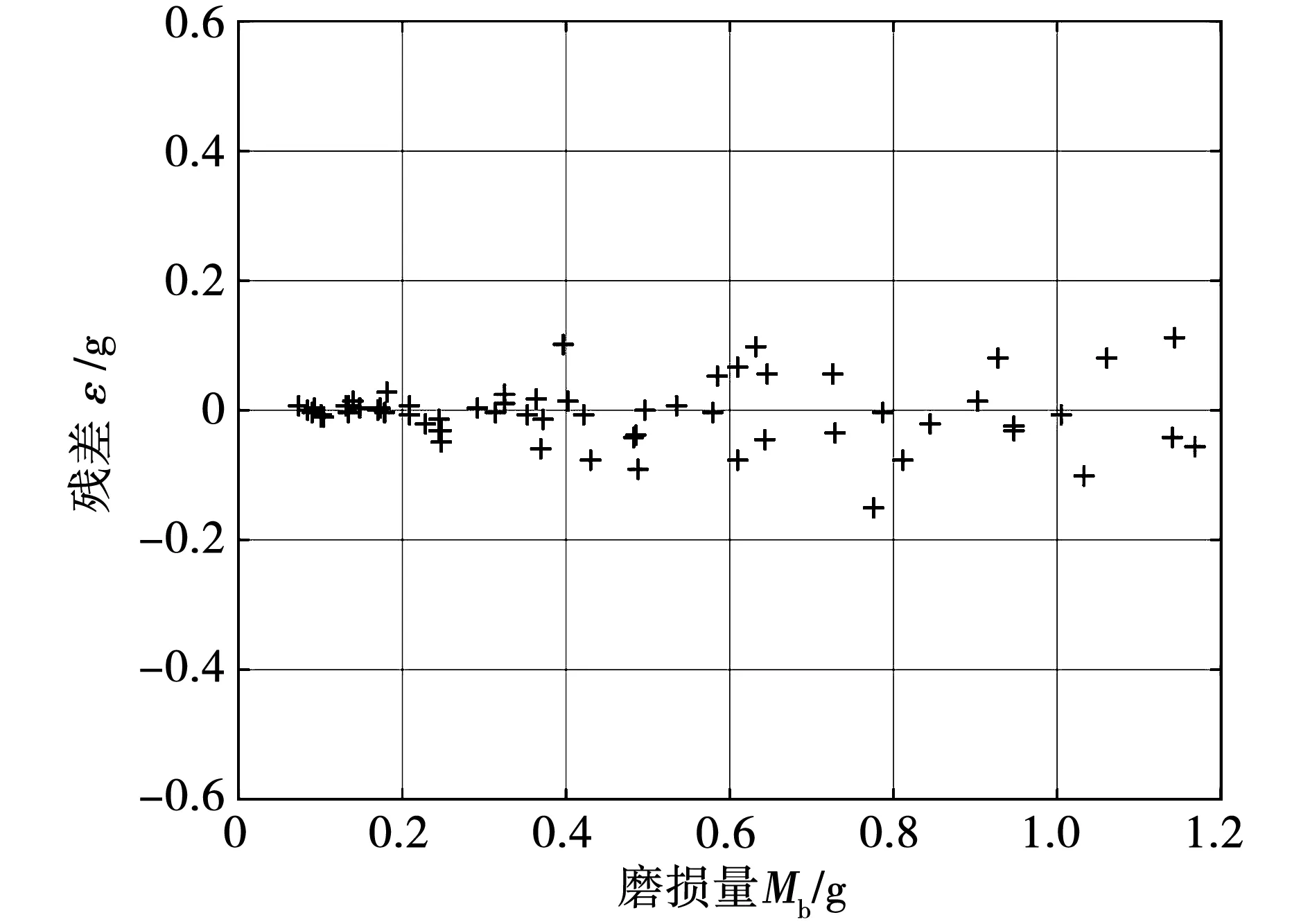
图11 实验数据的残差图

残差的计算公式为

(18)

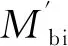
由图11知，实验点的误差都坐落在|εi|≤0.2带域内，误差较小，变化规律不规则，文中建立的基于改进的库伦-粘性摩擦力的磨损量模型可以对盐雾试验下的电刷磨损量进行预测。

当I=15 A、F=20 N、C=5%、T=35 ℃；I=25 A、F=20 N、C=5%、T=35 ℃；I=20 A、F=20 N、C=2%、T=35 ℃；I=20 A、F=20 N、C=4%、T=35 ℃时，分别在速度为v=300 r/min(4.7 m/s)、600 r/min(9.4 m/s)、900 r/min(14.1 m/s)、1 200 r/min(18.8 m/s)进行试验，以滑环圆周线速度为横坐标，电刷的磨损量为纵坐标，实验结果以及预测结果如图12所示。

从图12知，实验结果分布在所建立的基于改进的库伦-粘性摩擦力的磨损量模型曲线附近，最大误差出现在电流较小速度较大的测量点处，该处绝对误差达到4.9%，在允许误差范围之内，因此该模型可以用来预测电刷在不同条件下的单位时间的磨损量。由于实验设备及实验条件所限，该模型的适用速度范围不超过实验中采用的异步电机额定转速1 500 r/min。压力在电刷滑环系统恒压弹簧压力20 N附近，电流在电刷滑环工作电流20 A附近，盐雾浓度在中性盐雾试验标准5%NaCl浓度附近，环境温度为海洋环境下电刷滑环工作环境温度38 ℃附近。

5 结 论

1)文中搭建了基于盐雾试验机的双馈电机电刷滑环系统磨损量实验平台，该平台实现了电刷滑环系统和盐雾试验机的结合，模拟出海洋环境下电刷滑环系统不同工况下的腐蚀磨损情况，该设备实现了海洋环境下电刷的磨损实验，实验结果更加接近真实情况。

2)根据磨损理论，将改进的库伦-粘性摩擦力模型与电刷磨损量模型结合，建立电刷的磨损量预测模型，实验表明，接触电流，接触压力，盐雾浓度，实验温度以及速度影响电刷磨损。磨损量建模需将影响磨损量的接触电流，接触压力，盐雾浓度，实验温度以及速度因素引入模型，使模型更加准确。

3)采用粒子群算法进行参数辨识，可以辨识出模型中与接触电流，接触压力，盐雾浓度，实验温度相关的参数，经多项式拟合，得出电刷磨损量的预测模型。经由实验验证，该模型正确可靠，可以为运维人员提供一定的运维指导。

由于实验数据的有限性，该模型预测的结果与实测值之间存在一定的误差，但在允许范围之内，加大实验量和优化预测模型，可使得预测结果更加准确。更深远地，可以研究故障条件下电刷的磨损量模型。