基于GeoGebra分析一道中考压轴题的源与流

赵玉叶

(江苏省苏州市吴江区盛泽第二中学 215228)

中考数学试题由专家组精心命制而成，而数学压轴题历来在数学中考中占有举足轻重的地位．有些试题看似超乎寻常，实则抽丝剥茧后都能寻到基本的“知识源”，拥有很深的基础性和生命力．GeoGebra数学软件(简称GGB)具有动态、交互、开放、共享、简单、易用等特点，可以创建开放的探究环境，发挥教师的主导作用，体现学生的主体地位，实现静态向动态教学的转变．本文基于GGB软件分析2021年连云港中考数学27题这道动点轨迹压轴题，旨在对其解法进行分析并给出一些初步的思考，从思路摸索中感悟模型的根源，从猜想验证中体验本质的提炼，从可视化探究中思考问题的推广，实现压轴题的“寻源”与“显流”．

1 试题呈现

在数学兴趣小组活动中，小亮进行数学探究活动．

图1

(1)△ABC是边长为3的等边三角形，E是边AC上的一点，且AE=1，小亮以BE为边作等边三角形BEF，如图1．求CF的长.

(2)如图1，△ABC是边长为3的等边三角形，E是边AC上的一个动点，小亮以BE为边作等边三角形BEF，在点E从点C到点A的运动过程中，求点F所经过的路径长.

(3)△ABC是边长为3的等边三角形，M是高CD上的一个动点，小亮以BM为边作等边三角形BMN，如图2．在点M从点C到点D的运动过程中，求点N所经过的路径长.

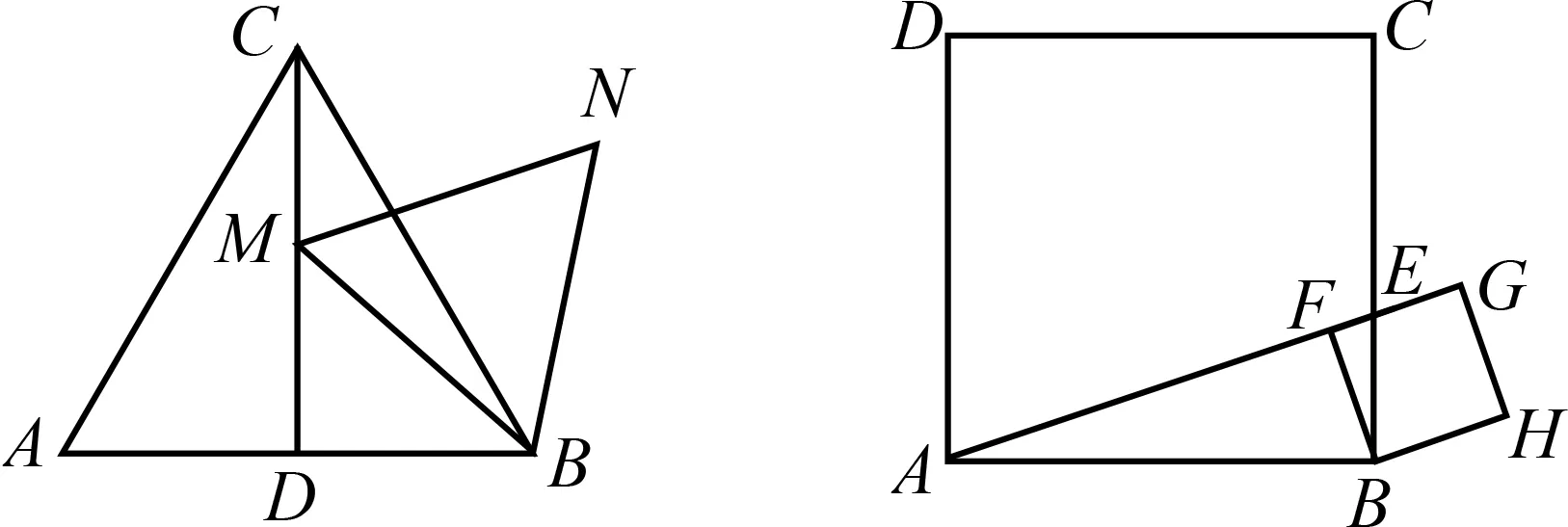
图2 图3

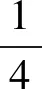
(4)正方形ABCD的边长为3，E是边CB上的一个动点，在点E从点C到点B的运动过程中，小亮以B为顶点作正方形BFGH，其中点F，G都在直线AE上，如图3．当点E到达点B时，点F,G,H与点B重合．则点H所经过的路径长为，点G所经过的路径长为．

第(1)小题是典型的全等三角形模型——“手拉手”模型．我们很容易证明△BAE≌△BCF(SAS)，求得CF=AE=1．

下面主要探讨第(2)～(4)小题．

2 寻源：方法初探——“按图索迹”

2.1 动点轨迹：模型归纳

后三小题考查的是动点的轨迹问题．初中数学中的动点轨迹有两种模型：直线型、圆弧型．受函数图象画法三步骤的指引，解决动点轨迹问题可以分为三步：(1)画图，取3个特殊位置(一般是起点、中点、终点)；(2)连线，判断曲直；(3)求解，求动点路径的线段长或弧长．

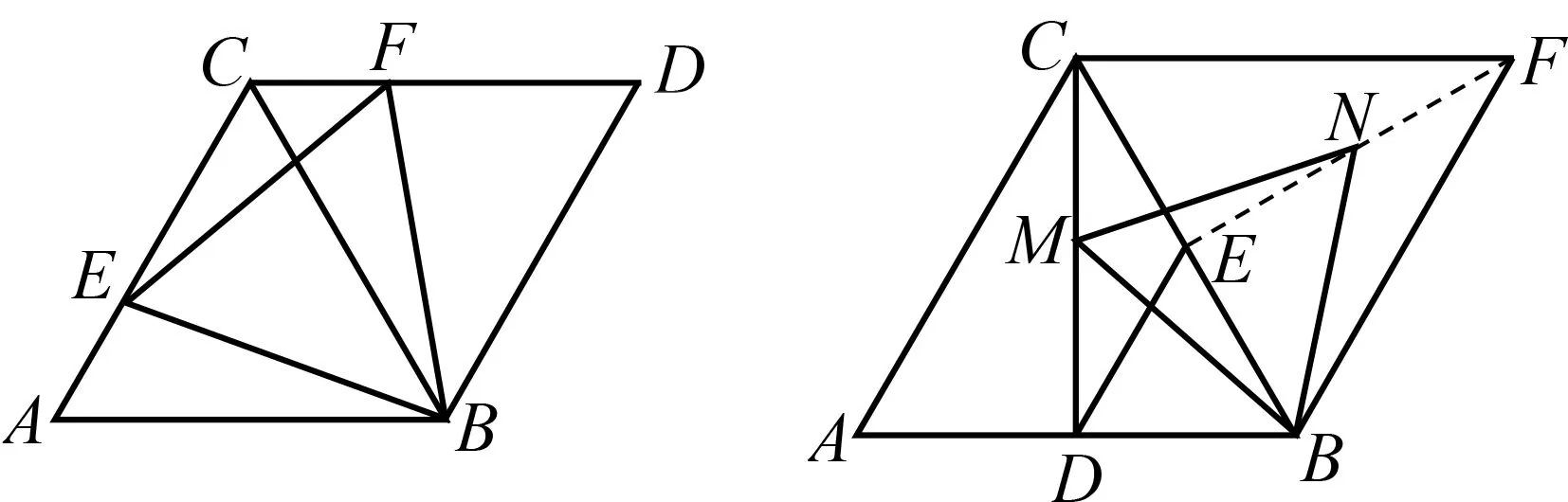
图4 图5

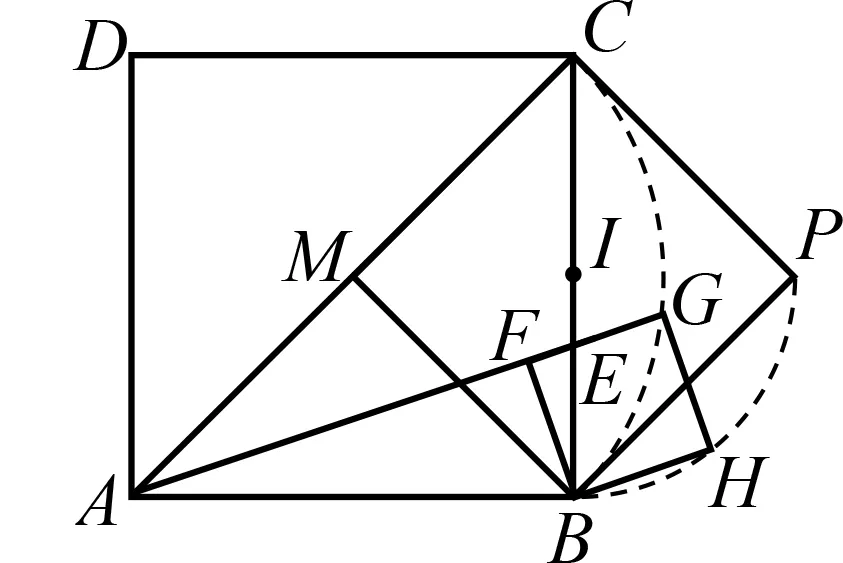
图6

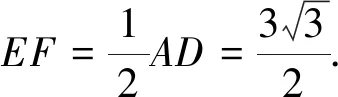
2.2 图形变换：本质提炼

上述常规解法需要画图确定动点的轨迹，所以比较费时费力．如果从图形变换的角度去思考动点轨迹的问题，往往可以发现从动点轨迹与主动点轨迹是有关联的．本题所有图形运动的实质都是旋转加位似，共同特征是正多边形共顶点．在这样的图形变换下都会形成“手拉手”模型．

如图7所示,第(3)小题中由围绕点B的四条“拉手线”BA=BC，BM=BN，就能找到△BAM≌△BCN(SAS)．所以点N的运动轨迹长等于点M的运动轨迹长DC．同理，如图8所示，第(4)小题中由围绕点B的四条“拉手线”BA=BC，BF=BH，能找到△BAF≌△BCH(SAS)，也就是点C，G，H三点共线．于是在Rt△ACG中，点G在以AC为直径的圆上，在Rt△BCH中，点H在以BC为直径的圆上．

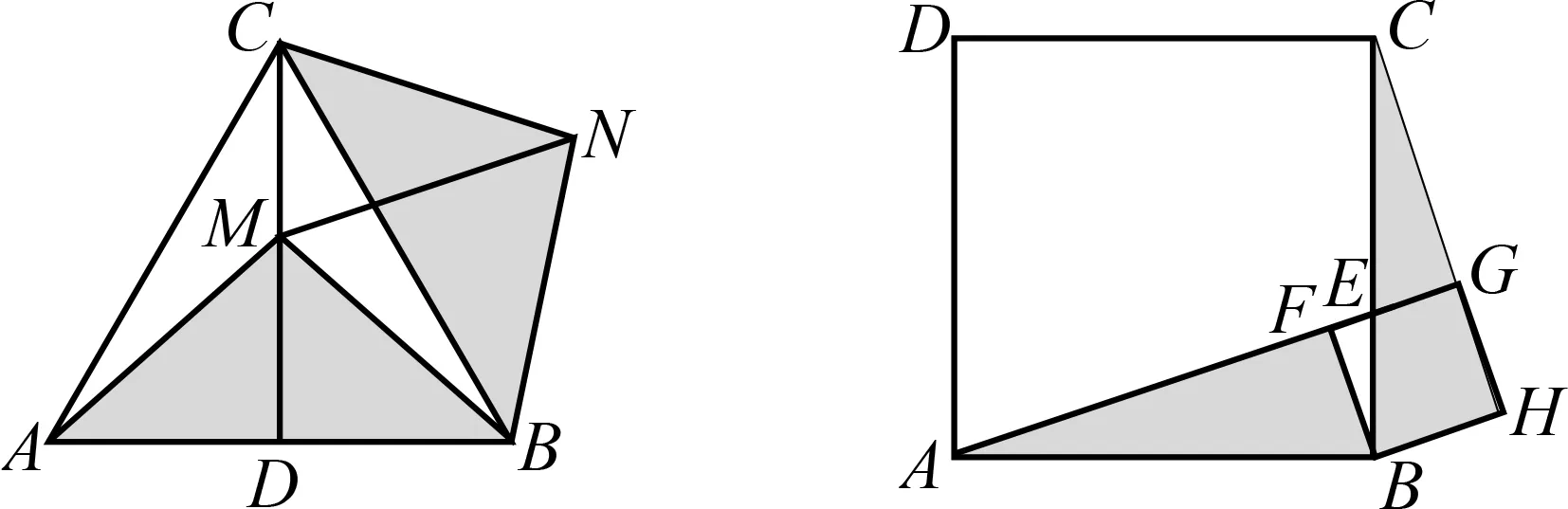
图7 图8

解题的成功要依靠正确思路的选择，要从最接近它的方向攻克．解初中的几何题理所应当提倡“以图为纲，按图索迹”．对于动点轨迹问题，我们可以从局部去分析动点的轨迹模型，判断直线型或圆弧型；也可以从整体出发关注图形变换(平移、对称、旋转、位似)．点动成线，线藏于形，解题时双管齐下，方可使思路并蒂开花．

3 显流：深度拓展——“按图索GGB”

数学家波利亚指出：“当你找到第一个蘑菇后，要环顾四周，因为它们总是成堆生长的．”在进行完上述探究过程后，学生对本题的动点轨迹和图形变换有了一定的认识与掌握，此时教师可以利用信息技术工具，向学生展示点的动态运动，并对其他特殊动点和一般化图形作进一步推广．下文探究“按图索GGB”的可视化拓展，利用GGB展开探索．

3.1 验：验证动点的轨迹

图9 图10 图11

3.2 探：探索其他的动点

问题1-1第(2)小题中等边三角形BEF的各边中点形成了怎样的轨迹？

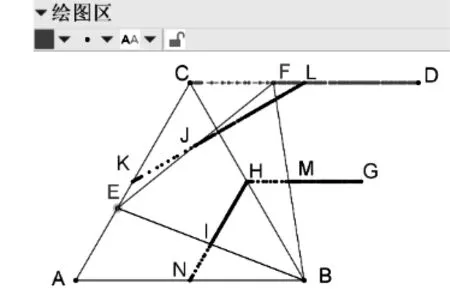
图12

先利用GGB探究：输入等边三角形ABC→在边AC上任取一点E→连结BE，输入等边三角形BEF→输入中点K,N,H→分别选择中点K,N,H关于动点E的轨迹．如图12，可发现各边中点的轨迹也是线段．

证明中位线NI中位线HM易证明△BCD是等边三角形，则菱形ABDC的中位线KL

问题1-2若将第(2)小题中等边三角形ABC和等边三角形BEF都换成一般三角形，那么第三个顶点的轨迹会有怎样的变化？

图13

先利用GGB探究：输入任意三角形ABC→在边AC上任取一点D→连结BD，标记∠BCD为α→顺时针旋转△BCD，旋转角为α→作位似三角形BED→选择点E关于动点D的轨迹．如图13，可以发现点E的轨迹不再与AB边平行，但保持直线型轨迹．

问题1-3若将第(2)小题中等边三角形ABC和等边三角形BEF都换成一般三角形，那么各边中点的轨迹会有怎样的变化？

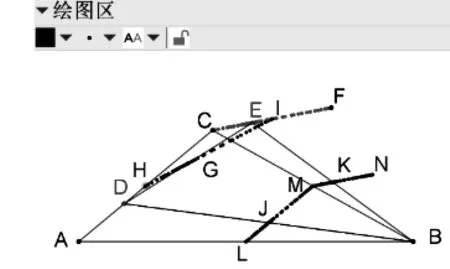
图14

先利用GGB探究：输入中点H,M,L→分别选择中点H,M,L关于动点D的轨迹．如图14，可发现各边中点的轨迹也是线段．

证明中位线LJ中位线MK中位线HI

问题2若将第(3)小题的中点D换成一般位置的点，其轨迹会有怎样的变化？

图15

先利用GGB探究：输入等边三角形ABC→在边AB上任取一动点D→连结CD，在边CD上任取一动点E→连结BE，输入等边三角形BEF→选择点F关于动点E的轨迹．如图15，拖动点D可发现点F的起点G随之运动，终点H保持不变，轨迹依旧呈现直线型．拖动点E，点F随之在线段GH上运动．

证明根据BD=BG，利用“手拉手”模型，我们容易证明△BDE≌△BGF(SAS)，所以点F的轨迹长GH等于点E的轨迹长CD．

问题3若将第(4)小题中动点E从边BC换到直线BC上，那么点G与H的轨迹会怎样变化？

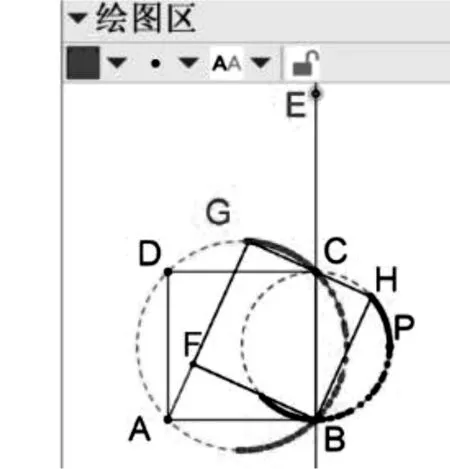
图16

证明在Rt△ACG中，点G在以AC为直径的圆上；在Rt△BCH中，点H在以BC为直径的圆上．

数学解题总是从分析已知元素和未知元素开始，二者的关联越不明显，就越值得探究．本道中考压轴题难度较大，区分度明显，学生很难观察出从动点与主动点的直接联系，更难将轨迹和图形变换分析出来．但运用GGB，学生能够直观地“看到”动点间的联系和要求的动点轨迹．具象化地展示试题的完成和拓展可以帮助学生认清试题本质、理解数学问题，有助于其养成反思的好习惯，落实“低起点，高落点”的目标．

4 结语

中考数学命题十分重视回归教材、重视基本知识，而中学数学教学的目的在于使学生掌握基础知识和基本技能，培养学生的数学能力，形成正确的解题思路和看题观点，这是中学数学教学的本源[1]．弗赖登塔尔认为：“数学知识不是教出来的，而是研究出来的．”学生解决问题的能力何尝不是如此呢？只有亲历问题的探索过程、锻炼科学的思维方式，才能在实践中逐步具备丰富的策略方法．教师根据教学内容和教学目标适时、适量地使用信息化平台，能够突破数学“难以意会，无法言传”的障碍，真正做到“教懂、教活、教深”[2]，引导学生将更多精力集中在高层次的数学思考上，实现有意义的解题教学，促进学生的思维发展．