微小卫星推力器姿轨一体化控制技术研究
刘燎,吴爱国,孙华苗,魏世隆,谢成清
(1.哈尔滨工业大学(深圳)机电工程与自动化学院,广东 深圳 518055;2.深圳航天东方红卫星有限公司,广东 深圳 518064)
0 引言
微卫星的质量一般在10~100 kg[1],其主要特点为质量小、体积小、制造发射成本低、功能针对性强,而现代微小卫星的发展特别需要轻量化、低功耗、小型化、集成化的部件[2]。推力器是航天器姿态和轨道控制中最常用的执行机构之一,它通过喷气产生控制力来控制卫星的姿态和轨道。利用推力器控制卫星三轴姿态,要求推力器能够产生6 个方向控制力矩[3],而单个方向控制时不对其他方向产生干扰,则至少需要安装6 个推力器,如果同时考虑冗余还需要增加推力器的配置。但是,推力器数量增多会导致姿态控制系统复杂,同时也给整星的安装带来一定难度,尤其不适用于微小卫星,因为其对各个设备的质量、成本和功耗均有严格的限制。文献[4-5]针对推力器构型和分配算法进行了研究,文献[6]针对多推力器的卫星姿态控制问题,设计一种推力器分配算法,可有效减小推力器燃料的消耗。由于整星重量功耗的限制,推力器配置少必然会导致可靠性不佳;由于微小卫星一般寿命要求短,推力器的配置上暂不考虑推力器失效的情况,因此传统的高冗余推力器配置方式不适用于微小卫星的配置。为了减小推力器的质量和体积,通常会减少推力器个数,同时提高微小卫星控制系统的功能密度,单个推力器能产生多个方向的控制力矩,这就会导致三通道控制力矩之间相互关联,会引起三通道间推力器的局部耦合[7-9]。在布局耦合问题中,通常存在单个喷气发动机开启时能够同时提供2 个或者3个通道的控制力矩,这种布局耦合使得微小卫星的姿态控制变得更加困难[10]。
针对微小卫星的特点以及姿态和轨道控制需求,本文设计了一套应用于三轴稳定微小卫星的姿轨一体化控制方案,采用星敏和陀螺的Kalman 滤波方案进行姿态确定,推力器采用斜装的方式在轨道控制中兼顾三轴姿态控制。针对斜装推力器喷气导致的三轴耦合问题,采用基于倾斜开关线的相平面控制,按照X轴最优策略进行控制,该方案在满足姿轨控的同时可实现姿轨控推力器的最小配置,减小了对飞轮角动量的需求,提高了控制系统的功能密度。
1 控制方案设计
卫星的控制系统由执行机构、敏感器和星载计算机组成,其中执行机构由推力器组成,敏感器由星敏和陀螺组成,星载计算机负责部件的通讯及控制指令的计算和生成,控制系统组成框图如下图1所示。

图1 推力器姿态控制系统组成框图Fig.1 Block diagram of the thruster attitude control system
星敏感器和陀螺分别敏感星体姿态和角速度信息,基于Kalman 滤波算法进行星体的姿态信息计算,得到星体的姿态四元数和角速度信息。星载计算机通过姿态信息和指令姿态信息生成姿态角和角速度误差信息输入相平面控制器,相平面控制器采用基于倾斜开关线的分区控制方式计算力矩状态,根据推力器分配斜装推力器的开关,并驱动相应的推力器进行喷气,控制相应的星体轴姿态,完成星体的闭环控制。
1.1 姿态确定方案
敏感器选用陀螺和星敏,采用Kalman 滤波算法进行姿态确定,生成估计的姿态四元数qe和姿态角速度ωe,指令生成器根据任务要求升成参考姿态四元数qc和姿态角速度ωc,误差姿态角θerr和误差姿态角速度ωerr作为输入提供给相平面控制器。每个轴通过相对独立的相平面控制器进行控制,相平面控制器生成相应的选择状态:正力矩(+1)、零力矩(0)和负力矩(-1)。将选择状态转化成相应的推力器开关指令驱动相应的推力器开关,从而完成星体的闭环控制[11]。其中误差姿态角的计算公式如下:


1.2 推力器布局方案
执行机构由5个推力器配置组成,其中1个1.0 N推力器主要用来进行轨道控制,其他4 个0.2 N 推力器采用斜装的安装方式提供3 个方向的控制力矩,兼顾轨道和姿态控制,1.0 N 推力器安装在-X面,能产生沿+X面的推力,4 个0.2 N(#1、#2、#3、#4)推力器也安装在-X面,存在一定安装角,在轨道控制中能产生+X面的推力,同时能产生三轴姿态控制力矩,其安装示意图如图2 所示,图中XYZ为星体坐标系。1.0 N 推力器进行轨道控制,4 个0.2 N推力器兼顾轨道控制和姿态控制,4 个小推力器采用关调制的形式工作,基于开关线的相平面控制器保持轨道机动中的姿态[12-15]。
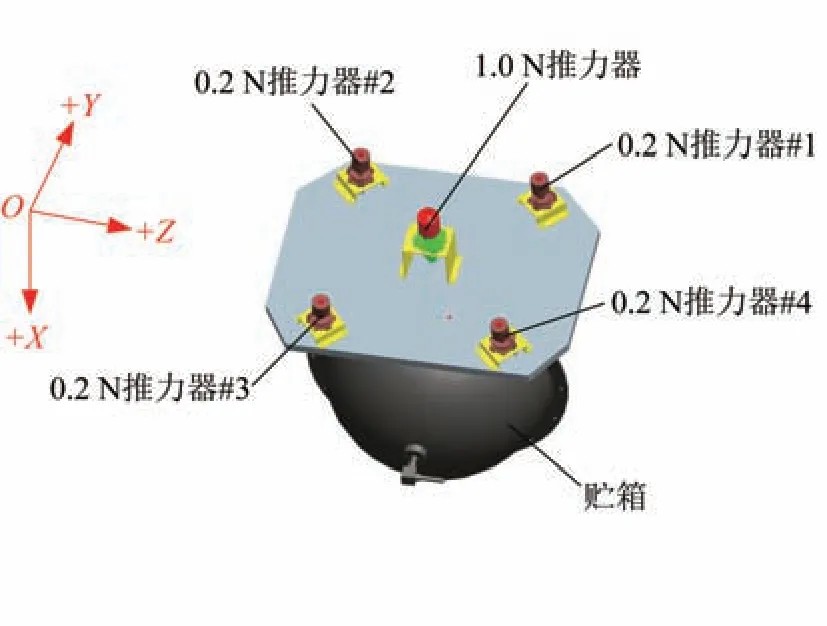
图2 推力器安装示意图Fig.2 Schematic diagram of thruster installation
推力器产生的推力矢量和力矩矢量在卫星星体坐标系中的坐标见表1。

表1 推力矢量和力矩矢量Tab.1 Thrust vectors and torque vectors
采用推力器进行姿态控制经常采用2 种工作模式:开调制和关调制,其中开调制主要用来进行正常的三轴姿态机动,关调制主要用来进行轨道控制中的三轴姿态维持。
本文暂不考虑采用开调制进行姿态机动,只对轨道控制的关调制进行分析,其中1.0 N 推力器为轨控推力器,轨控过程中为全开状态,4 个0.2 N 推力器兼顾轨道控制和姿态控制。
1.3 推力器控制方案
推力器的分配原则为:根据开关相平面控制器得出的三轴指令力矩后,按照X轴优先级最低的原则进行推力器的分配,即在推力器的分配中优先保证推力器组合产生的控制力矩能满足Y轴和Z轴的期望力矩。
由于推力器安装在-X轴,+X轴控制力矩偏差引起的滚转角偏差不会影响轨道控制效果。基于开关线的相平面如图3 所示,将相平面分为Ⅰ区:正向力矩全开区;Ⅱ区:正向力矩半开区;Ⅲ区:负向力矩半开区;Ⅳ区:负向力矩全开区;Ⅴ区:停控区。图中:±RS、±RV、±R1、±R2、l1、l2、l3、l4为开关线分界线;±AD、±AB为角度判断阈值。

图3 基于开关线的相平面Fig.3 Phase plane based on the switching lines
对于三轴开关状态[+10 -1]总共有27 种组合模式(3×3×3=27),按照上述分配原则,根据相平面控制器得出的三轴开关状态。例如:对于序号2,三轴指令状态为[0 1 1],结合表1 推力器产生的力矩矢量,优先满足Y轴和Z轴的期望力矩状态,按照燃料消耗最小原则,只开推力器1,满足Y轴和Z轴力矩状态。按照此分配原则得出的推力器开关形式见表2。

表2 推力器开关状态Tab.2 Thruster switch status
2 实例验证
仿真参数:轨道类型,圆轨道;轨道高度,500 km;轨道倾角,98.2°;轨道偏心率,0;升交点赤经,0;发射时间,2020 年1 月1 日,卫星质量,50 kg;推进剂类型,无水肼。
仿真条件:卫星12 500 s 时根据指令从对地定向模式进入轨道机动模式,开始轨道控制;仿真过程历时1 300 s,其中前500 s 用于轨道机动前的姿态调整,使推力器推力方向沿卫星在轨前进方向,后800 s 完成轨道机动控制,即轨控开机时长800 s,5 个推力器同时工作;推力器方向安装偏差为0.3°(3σ),位置偏心3 mm,0.2 N 推力器比冲为1 862 N.s/kg(190 s),1.0 N 推力器比冲1 960 N.s/kg(200 s)。仿真曲线如图4~图7 所示,每周期推力器指令开启时间设为0.05 s。
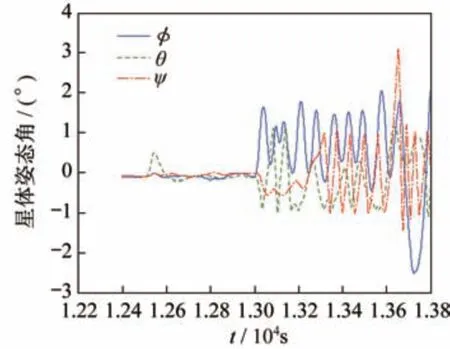
图4 卫星姿态角时间曲线Fig.4 Time curves of the satellite attitude angles

图5 卫星轨道角速度时间曲线Fig.5 Time curves of the satellite attitude angular velocities

图6 卫星轨道高度时间曲线Fig.6 Time curve of the orbit height
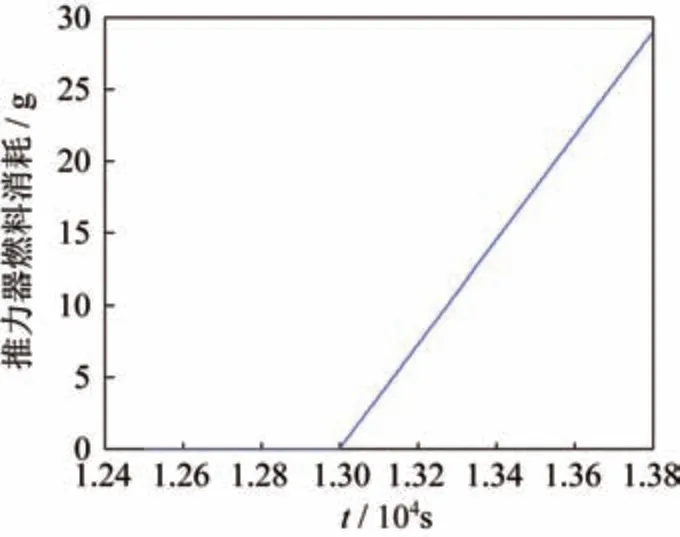
图7 燃料消耗时间曲线Fig.7 Time curve of fuel consumption
仿真结果表明:在轨控过程中三轴姿态角最大偏差可达3°,滚动角速度最大偏差可达0.3(°)/s,在800 s 内,轨道高度升高了2 km,推进剂消耗了28 g,能够正常进行轨道控制。XYZ轴相平面曲线如图8~图10 所示。

图8 X 轴相平面曲线Fig.8 Phase plane curve of the X-axis

图9 Y 轴相平面曲线Fig.9 Phase-plane curve of the Y-axis
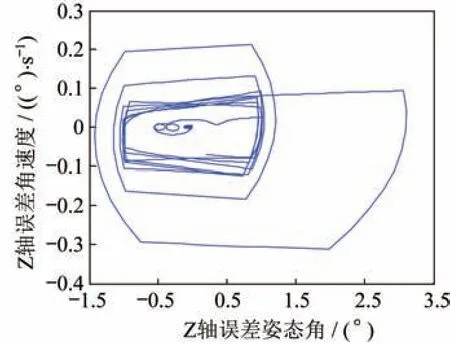
图10 Z 轴相平面曲线Fig.10 Pphase plane curve of the Z-axis
仿真结果表明:在轨道控制期间,误差姿态角和误差姿态角速度组成的相平面曲线为一闭合曲线,姿态控制处于收敛状态,卫星三轴姿态能够满足轨道机动的需求。
3 结束语
本文对微小卫星基于推力器的姿轨控一体化控制方案进行了研究,主要对推力器的安装方式进行分析,研究了斜装推力器在轨控过程中姿态保持的控制方法,采用基于开关线的相平面方法进行控制,根据XYZ轴力矩的正负,按照X轴优先级最低的策略对推力器开关进行分配,同时对某仿真条件下的卫星轨控进行了仿真。本文的控制方案能够显著提高控制系统的功能密度,但是未考虑推力器失效的情况,如何在增加最少推力器的情况下显著提高控制系统的可靠性可作为下一步研究内容。
后续还可以利用基于力矩分配的控制方法进行斜装推力器控制,主要的原理是:4 个推力器力矩矢量以卫星质心为原点将指令空间分为4 个区域,每个区域都由3 个推力器力矩矢量定义的3 个面界定,任意一个控制力矩矢量只可能位于这4 个空间区域的其中一个,并且仅由定义该区域的正力矩分量表示,即控制力矩矢量,可以仅采用3 个推力器实现,且保证其工作时间为正值。

