基于Levenberg-Marquardt Feed-forward Back Propagation神经网络的敏感性分析方法＊

姜强 刘天才 李宗洋 杨宏伟

（1.中国原子能科学研究院，北京 102413；2.中核战略规划研究总院，北京 100048）

引言

敏感性分析的目的是描述模型响应值受每个输入变量或输入变量组合不确定性的影响。有多种算法可用于进行敏感性分析。例如，计算输入变量样本与输出样本的相关性（基于相关性的度量）、模型在给定点的偏导数值（线性化方法）等。总的来说，敏感性分析算法可以分为三类：基于样本的方法、线性化方法、全局方法。

（1）基于样本的方法：基于对模型可用的蒙特卡罗样本后处理，得到敏感性分析结果，不需要特殊的采样方法。典型的方法有：输入/输出相关性方法（Input/output Correlation Method）、标准回归系数方法（Standard Regression Coefficients Method）等。

（2）线性化方法：基于假设模型是线性并进行模型评估得到敏感性分析结果。此方法无法识别输入变量之间的非线性行为和高阶交互。典型的方法有：微扰法（Perturbation Method）、Cotter方法等。

（3）全局方法：多为方差分解方法，根据单个输入变量或其组合的贡献来分解模型输出的方差。典型的方法有：Morris方法、Borgonovo指数方法、ANCOVA指数方法等。

本文提出基于LM神经网络的敏感性分析方法，分析LM神经网络算法与敏感性分析之间的理论关系，基于不确定量化分析工具UQLab[1]生成分析样本并计算量化的敏感性分析结果，通过对结果的对比分析，验证方法分析的可靠性并进一步讨论样本数量对计算结果的影响。

一、LM神经网络算法与敏感性分析

为了说明LM神经网络算法与敏感性分析的关系，首先考虑一个多元函数：

其中，L是感兴趣输出，xi是输入参数。

令输入参数的变化量分别为 Δx1,Δx2,...,Δxi,Δxn，感兴趣输出的变化量为 ΔL。根据多元函数的泰勒展开式可得：

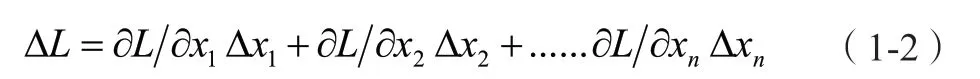
定义L对xi的敏感度Si为L的变化率与参数xi变化率之比。Si的数值可以通过下式计算：

其中，xi与L值均为已知参数，因此，敏感性量化分析的核心是求解多元函数f(x1,x2,...,xi,xn)关于输入参数的一阶偏导即Jacobian矩阵。

LM神经网络算法是被设计为接近二阶训练速度而不必计算Hessian矩阵的算法。当神经网络性能函数具有平方和的形式时（在训练反向传播网络中是典型的），Hessian矩阵可以近似为

并且梯度可以计算为

其中J即是Jacobian矩阵，包含关于权重和偏差的网络误差的一阶导数，e是网络误差的矢量。

LM神经网络算法以类似Gauss-Newton算法对Hessian矩阵进行近似

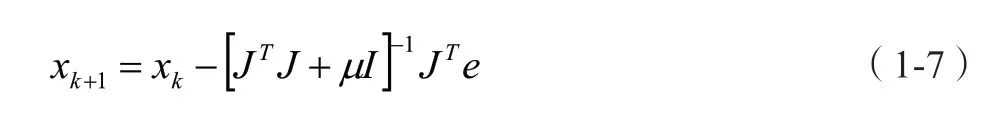
同时通过标准反向传播技术并在最后一层附以一个修改来计算Jacobian矩阵

上式中矩阵的每列是灵敏度矢量，通过网络反向传播产生一行Jacobian行列式。

根据LM神经网络算法的特点，训练神经网络得到的权值即能反映模型的敏感性。由此提出了基于LM神经网络算法的敏感性分析方法，以下采用不确定性量化分析工具得到的样本及已有的敏感性分析结果对方法进行验证。

二、基于LM神经网络算法的敏感性分析方法验证

1.敏感性分析结果

本文以堆芯子通道模型作为验证计算实例，选择通道冷却剂入口温度、线功率、系统压力、格架位置、平均入口质量流速作为不确定性源，其概率密度分布函数见表1，其中，X1表示平均值，X2表示标准差，标准差大小均为平均值的1%。基于不确定性量化分析工具生成3000个样本，并应用输入/输出相关性（Input/output correlation）、标准回归系数（Standard Regression Coefficients）、Morris等敏感性分析方法，得到结果如表2所示。

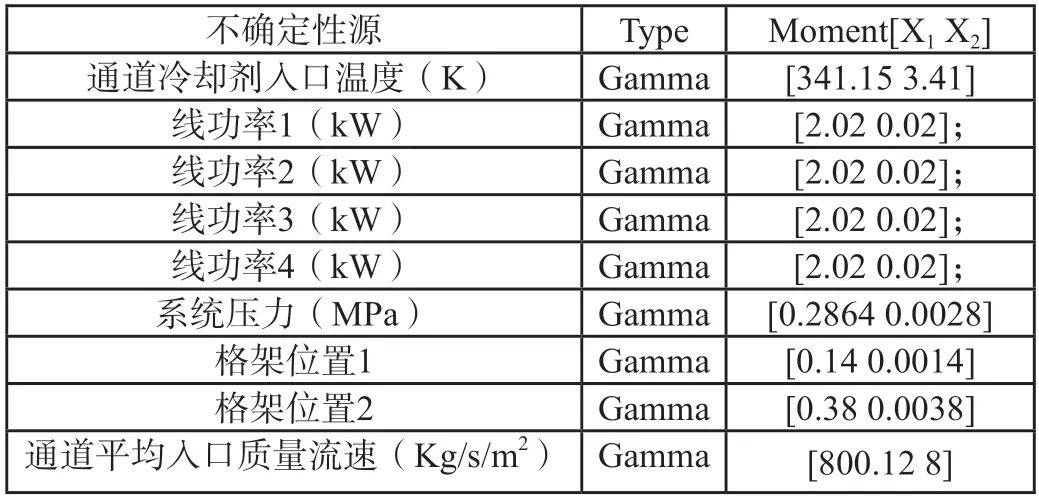
表1 不确定性源概率密度函数分布

表2 敏感性分析结果表

2.基于LM神经网络算法的敏感性分析

基于得到的3000个样本，使用2层LM神经网络进行训练，如图1所示。以隐藏层包含10个神经元节点的LM神经网络为例，在神经网络训练完成后，得到表征输入到隐藏层即Jacobian矩阵的权重iw和修正Jacobian矩阵的最后一层的权重lw，如表3、表4所示。如上所述，表4矩阵的每列权重表征的是灵敏度矢量，用以修正表3相对应的行权重值。用表4作为行矩阵乘以表3，即可得到最终的敏感性结果，即

表4 修正Jacobian矩阵的权重lw

图1 神经网络图

具体值如表5第10行所示。使用同样的方法得到不同神经元节点时的敏感性分析结果，得到表5。

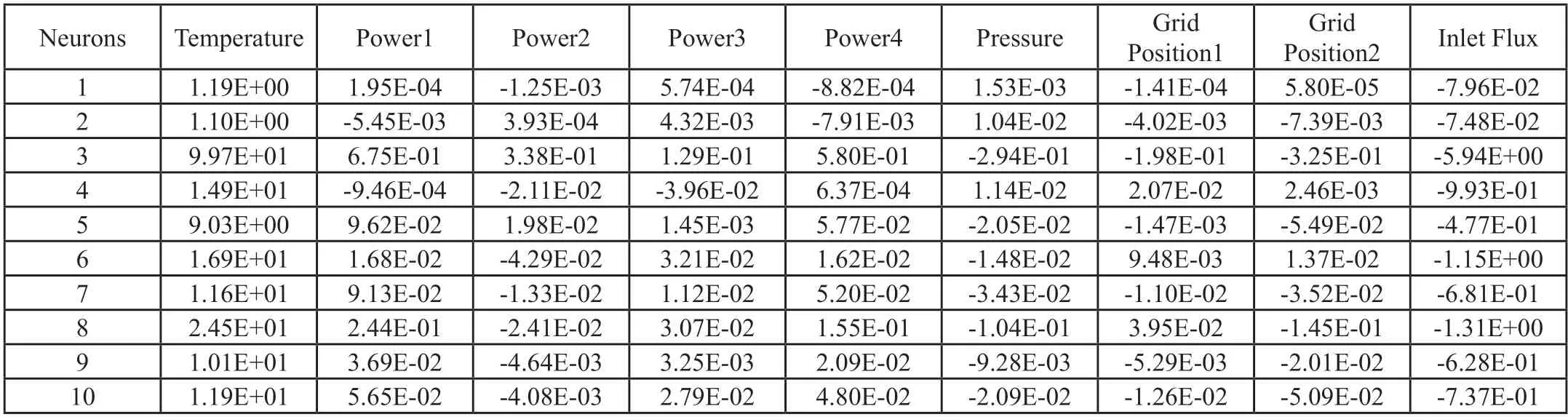
表5 不同数量神经元节点时的敏感性分析结果

考虑到不同方法得到的线功率、系统压力、格架位置的敏感性指数的值均极小，只对比不同方法得到的通道冷却剂入口温度、平均入口质量流速敏感性指数相对值。得到堆芯子通道计算模型敏感性相对指数图，如图2所示。

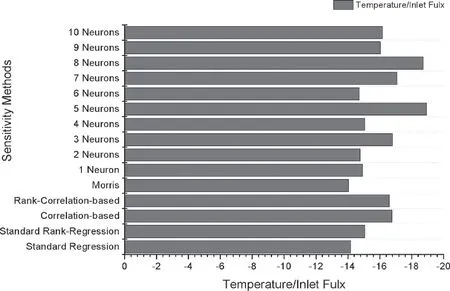
图2 堆芯子通道计算模型敏感性相对指数

在图2中，各方法得到的关于通道冷却剂入口温度、平均入口质量流速敏感性指数相对值相近，相关性结果相同，增加或减少隐藏层的神经元节点并没有显著的改变敏感性分析结果，基于LM神经网络的敏感性分析方法是有效的。

3.训练样本数对LM神经网络算法敏感性分析结果的影响

为了进一步讨论训练样本数对分析结果的影响，以10为步长，以10个样本数为起点，依次从3000个样本中随机选择对应数量的样本，以此作为神经网络新的样本。再使用不同数量神经元节点的2层LM神经网络训练样本，得到分析结果。同样只对比通道冷却剂入口温度、平均入口质量流速敏感性指数相对值，如表6所示。

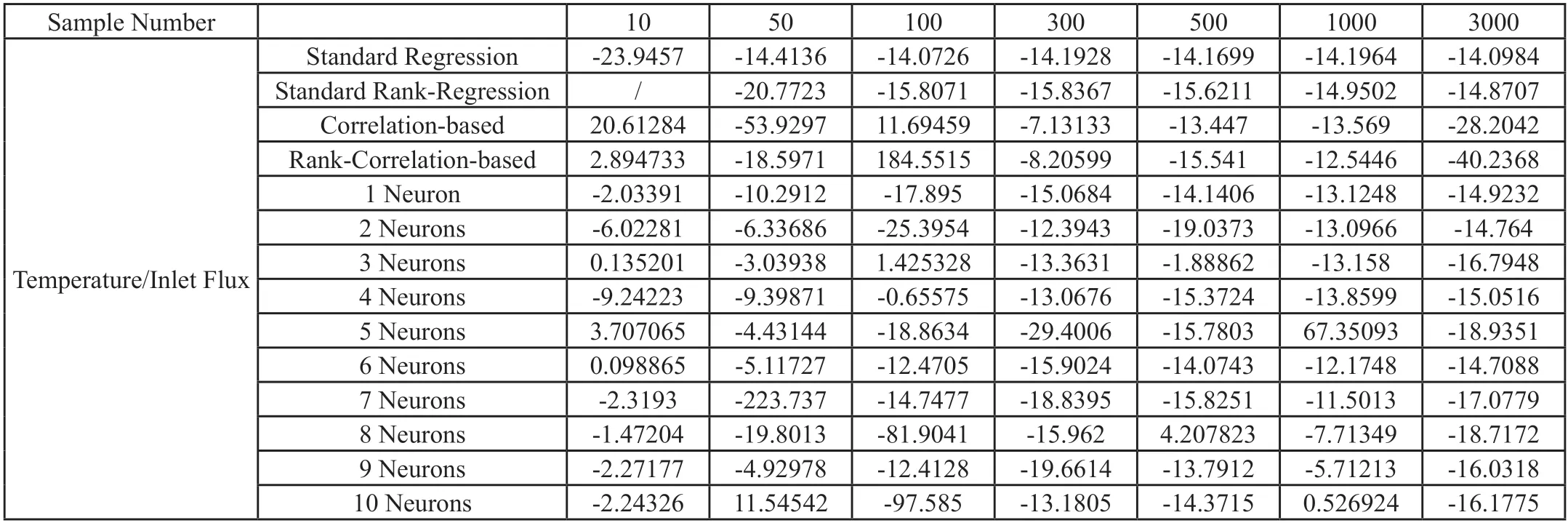
表6 不同样本数敏感性相对指数结果

在表6中，只使用一个神经元节点时，计算结果随样本数收敛速度极快，在样本数量达到20以后，敏感性分析结果就已趋于稳定值，稳定性极好。增加神经元节点后，计算结果的收敛性和稳定性变差。

结语

基于LM神经网络算法的敏感性分析方法是可用的，并具有准确性好、收敛快的特点。当使用隐藏层只包含1个神经元节点的2层LM神经网络时，敏感性分析结果随训练样本数收敛速度最快、稳定性最好。