基于动态选择技术的食品安全谣言不平衡数据集分类方法
何思宇 汪颢懿 左 敏 张青川
(北京工商大学农产品质量安全追溯技术及应用国家工程实验室 北京 100048)
0 引 言
不平衡数据集(Imbalanced Datasets)的特征是一个类的样本数量明显高于另一个类。这类数据在现实生活中非常常见,例如,在食品检疫中不合格品数量通常远小于合格品数量;在垃圾邮件过滤中垃圾邮件的数量往往小于一般邮件的数量[1];在欺诈交易识别中绝大部分交易是正常的,只有极少部分的交易属于欺诈交易等,诸如此类。
有关食品领域的食品安全谣言识别也是典型的不平衡数据集分类问题。有关食品的谣言,在因互联网普及而信息传播极快的今天,传播速度与范围也变得越加快而广。并且由于食品领域关系国计民生,为解决困扰食品领域的谣言识别问题,针对不平衡数据集开发健壮的机器学习过程十分重要。
通常,机器学习算法对数据集的每个样本都给予同等的重视,这使得它们在实验中偏向于大多数类[2]。这就产生了一个问题,因为从商业角度来看,在现实生活中少数类重要性往往要高于多数类。针对不平衡数据集开发的这些机器学习过程要考虑到数据分布的不平衡特性,并相应地进行处理。
动态选择(Dynamic Selection,DS)是一种技术,它生成一个分类器池,并根据在测试样本局部区域的预测能力,为每个测试样本选择一个基分类器或一组基分类器。动态选择是近年来一个活跃的研究领域,有研究称它优于一些更标准的分类器组合方法,如Boosting[3]。
近年来,已有一些学者对解决不平衡学习问题的不同方法进行了比较:He等[4]提供了可能是最广泛的关于不平衡学习方法的调查。Branco等[5]的工作建立在He等[4]开发的工作之上,并针对不平衡数据集而提出了一种新的分类方法。Krawczyk[6]描述了该领域的开放性研究问题,并指出了未来的研究方向。他们提出的一个建议是探索不同分类器的局部能力,并为每个分类器创建相应区域。这拓展了将动态选择方法应用于不平衡学习的思路。
本文打算探讨动态选择方法如何有助于解决不平衡学习问题,并提出一种新的动态分类器选择(Dynamic Classifier Selection,DCS)算法,称为多分类不平衡数据集动态分类器选择法(DCS-MI),专门针对多类不平衡数据集的情况,并将其最终运用到食品安全谣言识别中。
1 动态选择
1.1 动态选择简介
如前所述,动态选择(DS)技术首先生成一个分类器池,对于每个测试样本,根据它们在测试样本的局部区域内的预测能力,选择一个基分类器或一个分类器集合。该局部区域通常被称为胜任域,通常由k-NN算法确定。用于选择胜任域的数据集可以是训练数据集,也可以是验证数据集,称为动态选择数据集(dynamic selection dataset,DSEL)[7]。
总体而言,在动态选择中,一个新的查询样本的分类通常包括三个步骤:
1) 胜任域的界定,也就是说,如何定义查询样本xj周围的局部区域,在该区域中估计基本分类器的能力级别。
2) 确定用于估计基本分类器的能力水平的选择标准,如准确性、概率性和排名。
3) 根据估计的能力水平确定选择单个分类器(DCS)或分类器集合(DES)的选择机制。
1.2 动态选择算法分类
一般来说,动态选择算法可分为动态分类器选择(DCS)与动态集成选择(Dynamic Ensemble Selection,DES)两种类型。
图1反映了动态分类器选择和动态集成选择的过程。
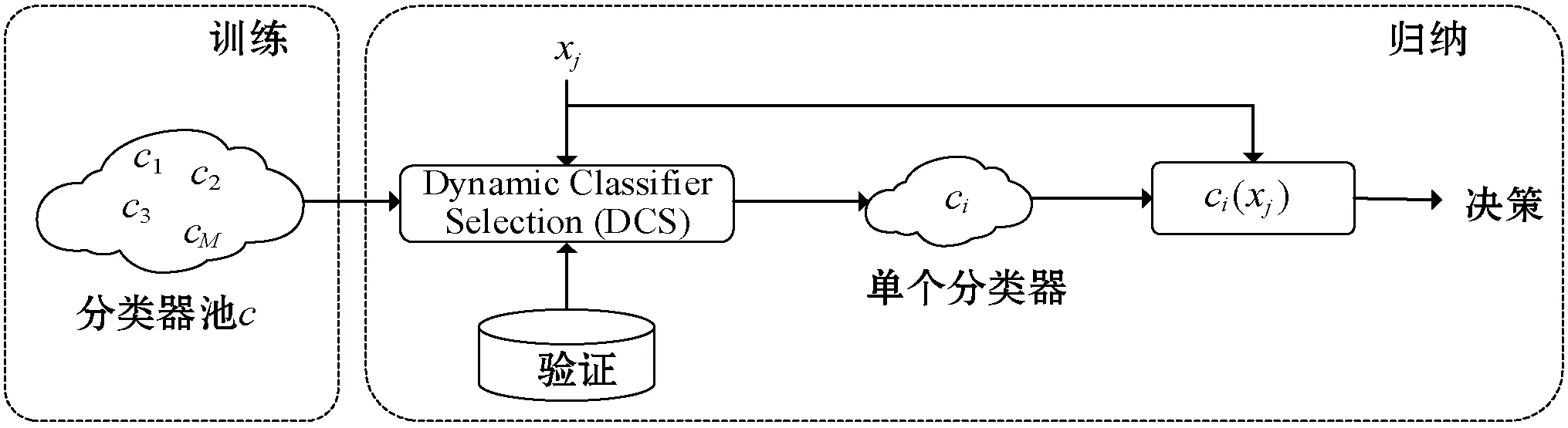
(a) Dynamic Classifier Selection(DCS)
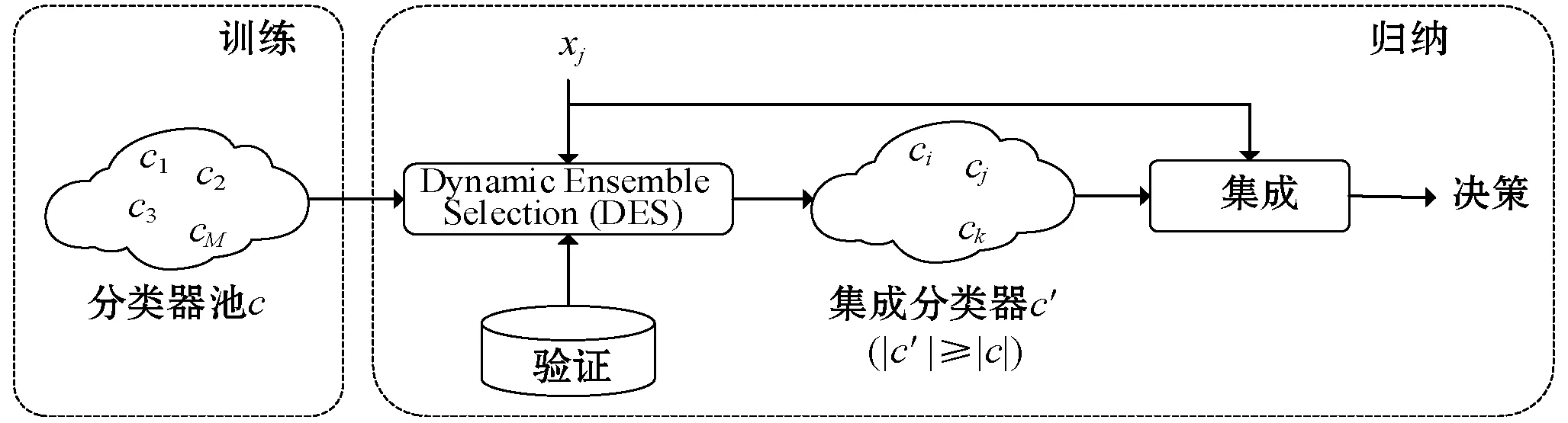
(b) Dynamic Ensemble Selection(DES)图1 动态选择算法示意图
动态分类器选择技术是为每一个测试样本选择最优单个基分类器的技术,其中典型的算法有:
算法1局部分类器精度[7](Local Classifier Accuracy,LCA)技术,针对每个测试样本x,在胜任域内选择精度最高的基分类器。
算法2改进的分类器排名[7](Modified Classifier Ranking,RANK)技术,它选择的基分类器能够正确地预测连续最近邻的最大数量。
而动态集成选择技术则是选择合适的集成基分类器组合的技术[8],其中典型的算法有:
算法3KNORAU[9](Knora-Union)技术,它选择能够正确预测胜任域内单个样本的所有基本分类器集合。
算法4META-DES[7](Meta Dynamic Classifier Selection)技术,它将基本分类器的选择视为一个元学习问题。为了达到这个效果,它定义了一组元特征fi,与衡量基分类器ci预测样本xi能力的标准相对应。这些元分类器编码到一个向量vi,j,元分类器λ是训练有素的预测如果ci为xj做出正确的预测。
最近有研究称,与标准的集成机器学习技术相比,META-DES表现出了更好的性能。
算法5DES-MI[10](Dynamic Ensemble Selection for multiclass imbalanced datasets )技术:该算法利用随机平衡方法生成平衡的训练数据集。通过在验证数据集中运用k-NN算法选择胜任域Ω。然后,在Ω中的每个样本s,将num设为在Ω中同为类s的样本数量,以下是权重的分配计算公式:
式中:α是一个常数。考虑在胜任域内最准确的分类器的百分比,并对每个样本的准确性进行加权,然后作为一个整体进行选择。
2 不平衡学习
2.1 不平衡数据集
不平衡数据集是指在数据集中各类别样本数量分布比例不均衡,即某些类别的数量远大于或远小于其他类别。在出现此类数据失衡严重的情况时,使用传统标准机器学习算法处理不平衡数据集,会导致算法性能较差[11]。有研究表明,传统分类器在数据不均衡比例超过4 ∶1时就会偏向于大的类别[12]。
2.2 不平衡数据集处理
根据Galar等[13]的研究成果,不平衡学习方法可以分为三类:
1) 算法级方法尝试调整标准的机器学习算法,这样算法就不会偏向多数类而忽略少数类。
2) 代价敏感的方法可以通过在少数类的样本中引入更高的权重来调整数据,或者通过让分类器接受代价来调整算法,例如在分类器的损失函数中进行调整。
3) 数据级方法寻求通过对少数类进行过采样或对多数类进行欠采样来重新采样数据集。
但在实际应用中,算法级方法需要根据不同数据集进行调整,代价敏感学习代价也往往需要人为设定,没有普遍适用性。因此本文尝试从数据级方法出发,对数据进行处理,改变数据结构,以针对不平衡数据集提高分类器性能。
过采样(over-sampling)和欠采样(under-sampling)是两类数据处理方法。过采样方法即是对少数类的数据样本进行随机采样来增加少数类的数据样本个数;欠采样即是对大类的数据样本进行随机采样来减少大类的数据样本个数。
本文采用过采样技术中最具代表性的技术之一,合成少数类过采样(Synthetic Minority Oversampling Technique,SMOTE)[14]来进行数据处理。它克服了过采样的一些缺点,而且加强了原始数据,并已经被证明在很多领域解决不平衡学习问题都比较有效。
3 DCS-MI算法
3.1 Bagging集成算法
算法6Bagging[15]算法是集成学习中两大类算法中的一个代表算法,其学习器之间不存在依赖关系并且可以并行生成学习器。 Bagging 方法具有可以减小过拟合的优点,所以其通常被使用在强分类器和复杂模型上,并且往往能够取得良好的表现。
Bagging算法可以解决回归问题和分类问题。它从原始数据中随机抽取n个样本,抽取过程重复s次,产生s个训练集。在每个训练集上进行训练并得到一个弱分类器,最终会训练出s个弱分类器。预测结果将由这些分类器投票决定:
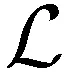
过程:
1: fort=1,2,…,Tdo
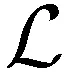
3: end for
输出:
3.2 SMOTE技术
算法7SMOTE[16]主要是基于数据集中现存的少数类样本,计算样本特征空间之间的相似度,以创建人工合成样本。其步骤如下:
1) 对于少数类Smin∈S中的样本,即xi∈Smin,计算它的k个近邻。
2) 通过计算n维空间的欧氏距离,得到距离xi最近的k个Smin中的样本数据。
3) 然后从k个近邻中,随机选择一个样本,产生人工合成的数据:
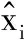
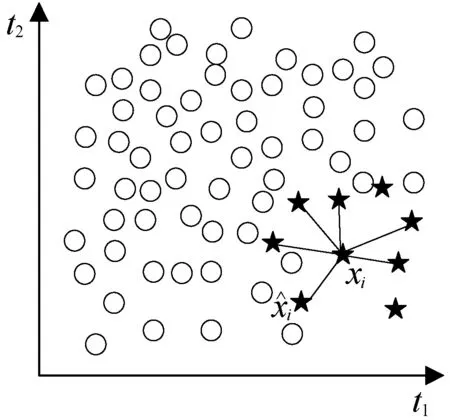
(a)
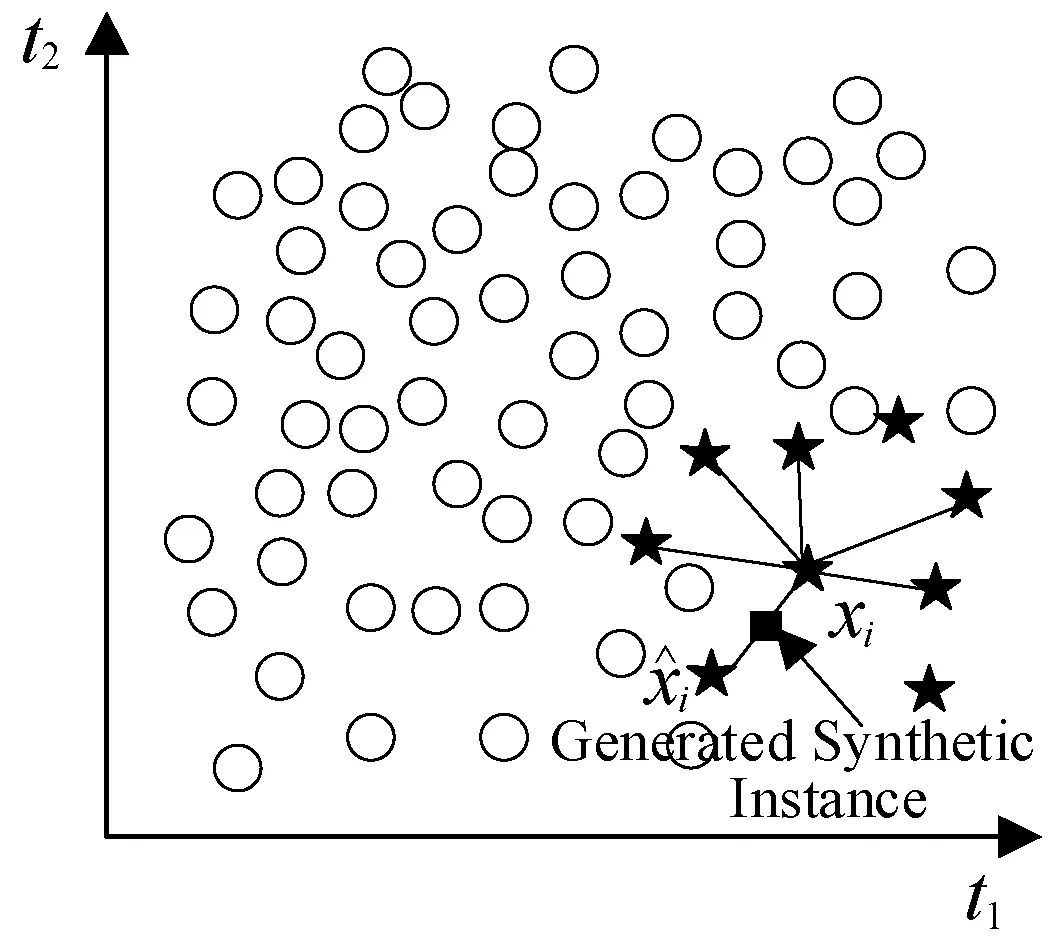
(b)图2 SMOTE采样具体过程
图2展示了SMOTE的具体过程。其中:(a)展示了一个典型的不平衡的数据,SMOTE中的k取值为6。(b)展示了一个随机产生的合成样本,这个样本是沿着和的直线产生的。这个随机点将被添加到数据集,然后重复此过程,直到达到所需的样本数量为止。
3.3 k-NN算法
算法8k-NN[17](k-Nearest Neighbor)算法是机器学习算法中最基础、最简单的算法之一。它既能用于分类,也能用于回归。
k-NN分类是通过测量不同样本之间的距离来实现。一般来说,在实践过程中,k-NN中的k值采用交叉验证的方式选取,而距离一般使用欧氏距离或曼哈顿距离:
欧氏距离公式为:
曼哈顿距离公式为:
k-NN算法可描述为:
1) 根据给定的距离量度方法在训练集T={(x1,y1),(x2,y2),…,(xn,yn)}中,找出与初始样本点x最近的k个样本点,并将这k个样本点所表示的集合记为Nk(x),其中:x为预测样本;xi∈X∈Rn为n维的样本特征向量;yi∈Y={c1,c2,…,ck}为样本的类别,i=1,2,…,N。
2) 根据多数投票的原则确定样本x所属类别y:
i=1,2,…,N,j=1,2,…,K
式中:I为指示函数。I计算如下:

3.4 DCS-MI算法提出
算法9将训练数据集进行适当的划分,这些训练集将用于训练基本分类器,验证数据集即本文的DSEL。在训练基分类器时,先在适当的训练集上使用Bagging算法,然后使用SMOTE技术来进行数据处理,这样在最后的数据集中,每个基分类器训练的每个类的频率是相同的。算法结构如图3所示。
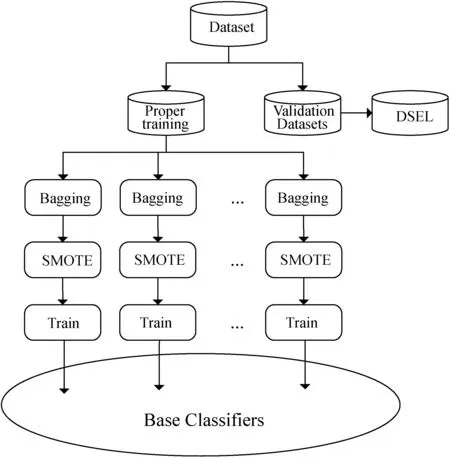
图3 DCS-MI概述
通过对DSEL应用k-NN算法来确定胜任域。胜任域内的每个样本都根据整个DSEL中同类样本的数量进行加权。假设cl(x)是样本x的类,num(c)是DSEL中c类样本的数量,则胜任域内每个样本x的权值为:
考虑其中一个分类器Ci,设Ci,c(x)是分类器Ci预测样本x属于c类的概率。于是,Ci在胜任域Ω中的损失如下:
最终,选择损失值最小的分类器来预测测试样本的分类。
3.5 DCS-MI算法时间复杂度
令tr为合适的训练数据集的大小,b为基分类器的数量,m为每个样本的特征数量。考虑到Bagging子过程的时间复杂度为O(tr),而SMOTE子过程的时间复杂度为O(m×tr2),最坏情况下生成基本分类器的时间复杂度为O(b×m×tr2)。
设v为验证数据集的大小,te为测试样本的数量,k为k-NN算法中使用的近邻的数量。应用k-NN算法的复杂度为O(v×m+v×k)。为每个类寻找权重的时间复杂度是O(v)。值得注意的一点是,只需要在开始时为类找到权重,而不是每次预测一个测试样本的类时。因此,在胜任域内寻找样本权值的时间复杂度为O(k),明显低于运行k-NN算法的时间复杂度。因此,预测测试样本类的时间由应用k-NN所需的时间决定。因此,为te测试样本选择基本分类器的时间复杂度为O(te×v×m+te×v×k)。
最后,不考虑基分类器的训练时间和预测时间,最坏情况下DCS-MI的时间复杂度为O(b×m×tr2+te×v×m+te×v×k)。
4 DCS-MI算法的实现与分析
本文通过实验比较了DCS-MI算法与一些最新的动态选择算法在4个公共数据集中的表现。在本文的实验中,合适的训练数据集、验证数据集和测试数据集的样本划分比例为60%、20%、20%。DCS-MI算法和用作对比的最新算法都使用了10个基本分类器,对于其中每种算法,包括DCS-MI算法,基分类器都是一个最大深度为10的决策树。
4.1 实验数据
本文使用了从Keel获取的4个公共多分类不平衡数据集。
1) 天平平衡数据集(B.S.):这个数据集是用来模拟心理实验结果的,样本内容包含天平的一端向右。一端向左或保持平衡。属性包括左权值、左距离、右权值和右距离。
2) 汽车评价数据集(C.E.):该数据集来自于一个简单的层次决策模型。该模型根据6个输入属性来评估汽车:购买、维护、门、人员、引导和安全;4个输出类别:不可接受、可接受、非常好和良好。
3) 心脏病数据集(H.D.):该数据集来自位于美国俄亥俄州克利夫兰的事务诊所的退伍军人,每个样本代表一个病人,数据集中包含14个属性。分类任务是预测病人是否患有心脏病。分类类别用0、1、2、3、4表示,其中:0表示没有心脏病;4表示患有心脏病的风险最高。
4) 页面块数据集(P.B.):这个数据集包含文档页面布局的块,它是由分割过程检测到的。分类任务是确定块的类型:文本(1),水平线(2),图形(3),垂直线(4)或图像(5)。
数据集信息见表1。
4.2 实验评价指标
在分类方法有效性评价中,准确率是经常被使用的评价指标。然而在不平衡数据分类中,准确率不再适合用来评价分类性能的好坏。例如,在二分类情况下,若是训练集的不均衡比例超过4 ∶1,即超过80%的样本是属于同一个类的,而训练过程中分类器将所有的训练样本都分类为数量占比大的类别,可以看出,尽管该分类器的分类准确率超过80%,实际上我们仍然认为该分类器是无效的。
类似的常用评价指标还有精度和召回率。同样假设在二分类情况下,分类器若将不平衡数据集中的所有样本都预测为少数类,其分类的召回率将达到100% ,但同时其精度将会很差;相反,若正确分类出很少的少数类,且又识别出所有多数类,则将达到很高分类的精度,却得到很低的召回率。
因此本文选用了3个分类绩效指标来对算法进行衡量:每个类平均的F1值,每个类平均的AUC值和Cohen’s Kappa值。
1) F1值。F1值是模型精确率和召回率的一种加权平均,它的取值范围是[0,1]。F1值能够对精度和召回率进行平衡,当F1值较高时,精度和召回率都能保证在较高的水平。
2) AUC值。AUC (Area Under Curve) 是一个数值,其定义为ROC曲线下的面积值。由数学推导可知,ROC曲线下的面积数值不大于1。又由于一般情况下ROC曲线在y=x直线的上方,因此可知AUC的取值范围一般为[0.5,1.0]。舍弃ROC曲线而采用AUC值作为评价标准,是因为AUC值相较于ROC曲线传达的信息,能够更清晰明了地进行解读,即对应AUC值更大的分类器效果更好。
3) Cohen’s Kappa值。Kappa值是1960年由Cohen等提出的,作为评价判断模型一致性程度的指标。Kappa值的取值范围为[0,1],Kappa值越大,代表一致性越强或分类精度越高。实践证明,Kappa值是一个描述数据结果一致性较为理想的指标,同时也可用于衡量模型分类精度,因此其在实验中得到了广泛应用。
4.3 实验结果
与本文提出的DCS-MI算法进行对比实验的为1.2节中介绍的LCA、RANK、KNORAU、METADES和DES-MI技术。表2、表3和表4给出了实验得到的结果,粗体展示的表示性能最好的技术。
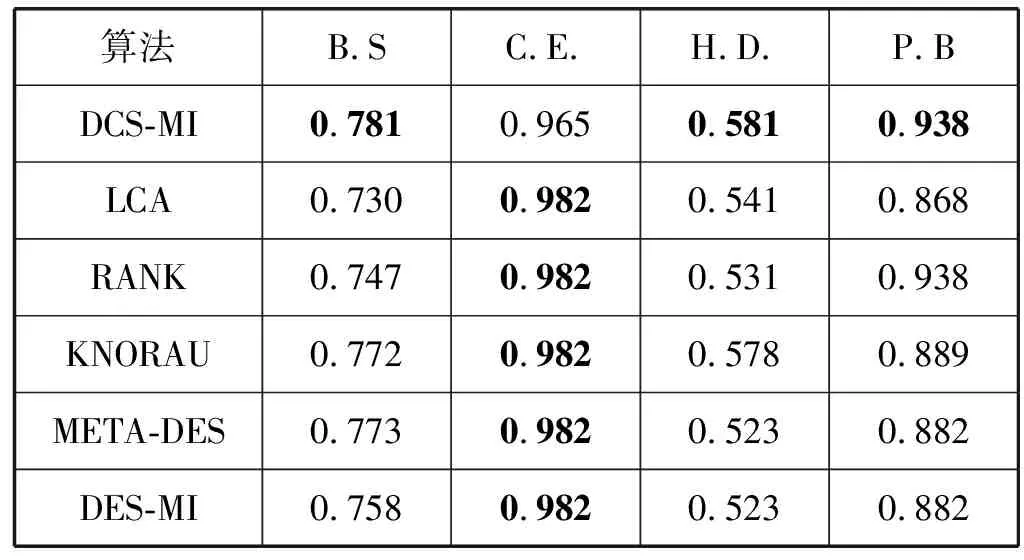
表3 平均AUC值
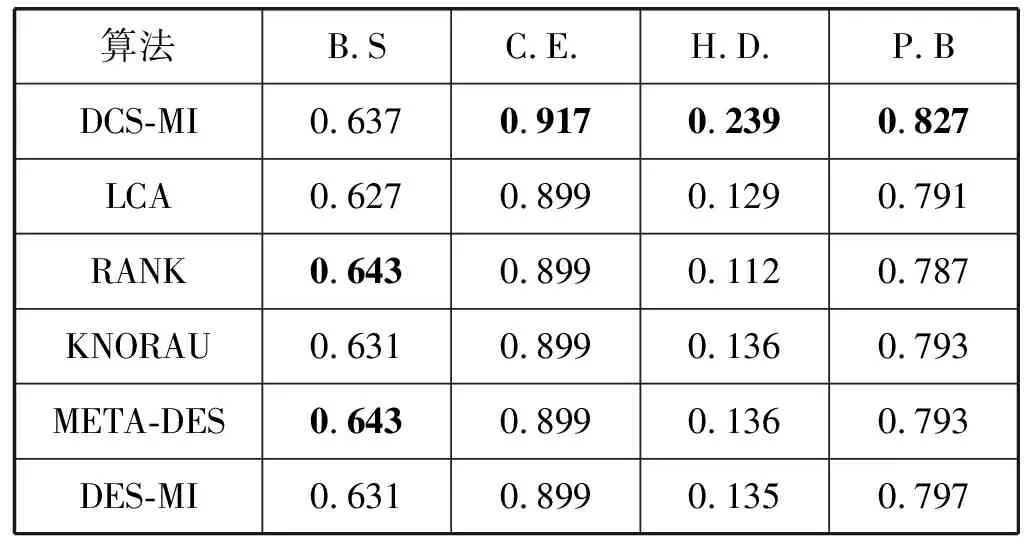
表4 Cohen’s Kappa值
4.4 结果分析
由实验结果可以看出,DCS-MI算法获得了12个数据集/度量对中9个的最佳结果。因此,与其他的动态选择技术相比,DCS-MI在处理多类不平衡数据集时具有较好的性能。
需要进一步注意的是,与DES-MI相比,DCS-MI算法在12对数据中有11对得到了相对更好的结果,而DES-MI是一种针对多类不平衡数据集的动态选择技术。对比结果如图4所示。
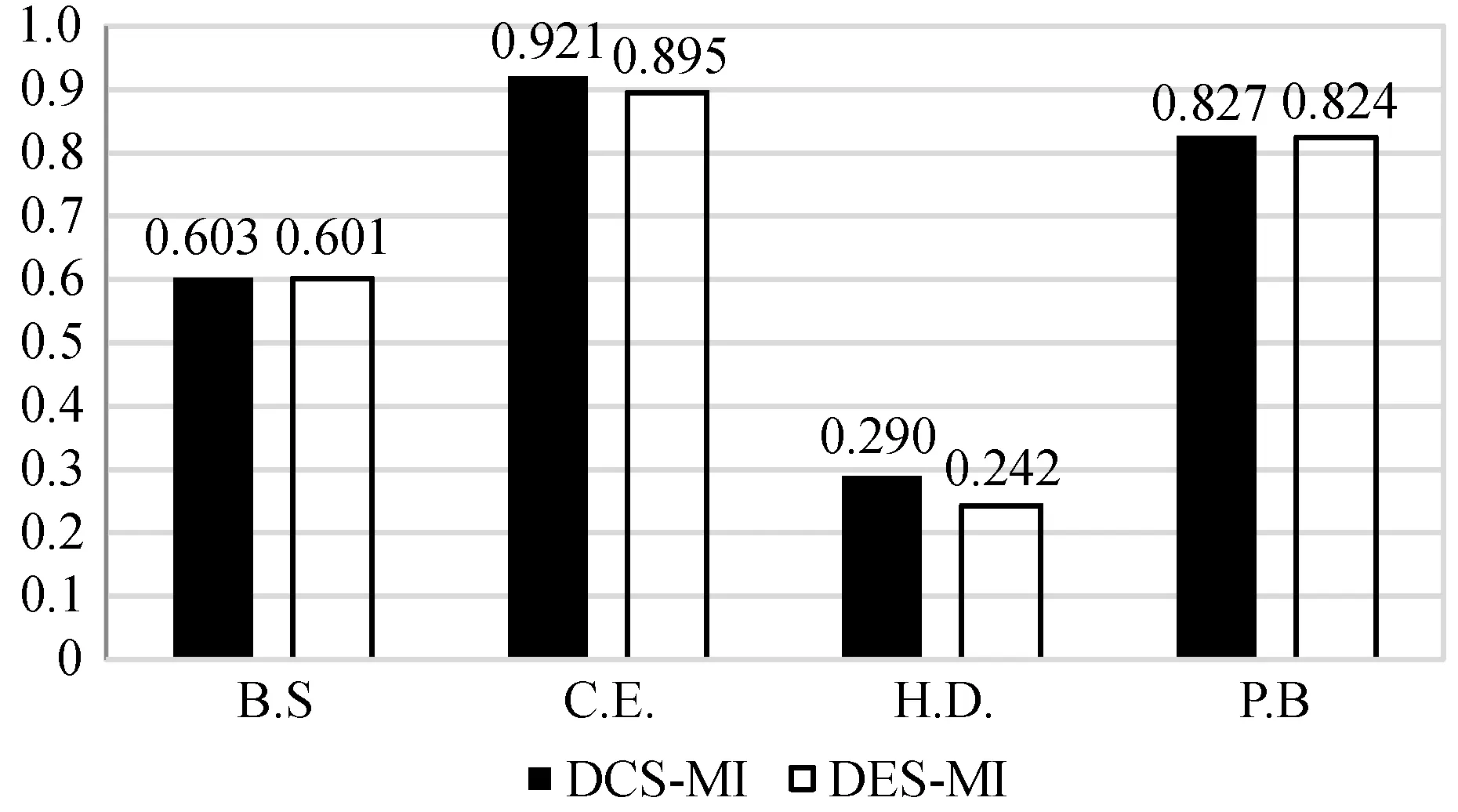
图4 平均F1值:DCS-MI和DES-MI
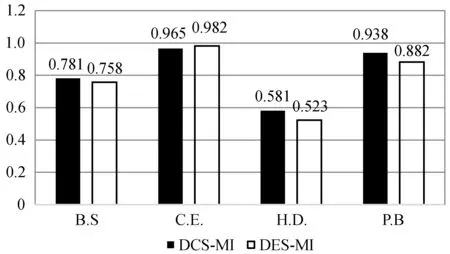
图5 平均AUC值:DCS-MI和DES-MI
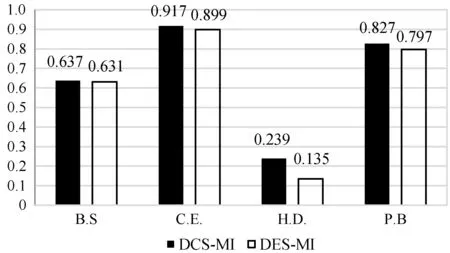
图6 平均Cohen’s Kappa值:DCS-MI和DES-MI
可以看出,DCS-MI算法即使是与专门针对多分类数据集而设计的算法相比,也表现出了更优越的算法性能。
5 DCS-MI算法实现食品谣言文本的识别分类
经实验验证了DCS-MI算法在公共不平衡数据集上取得了良好的性能表现。为进一步验证其在食品安全谣言文本分类方面的分类效果,本文通过网络爬虫获取食品安全新闻文本数据集,并进行实验。与此同时,为对比验证DCS-MI算法性能较传统机器学习算法性能在处理不平衡数据时的优越性,选取传统机器学习算法贝叶斯(Bayes)和随机森林(Radom Forest)作为对比实验。数据集结构如表5所示。

表5 食品安全新闻数据集分布
5.1 实验数据处理
获取文本数据后,首先进行分词处理。本文采用jieba分词工具对文本数据去停用词并进行分词。使用jieba将文本分割为字词后,再使用Word2vec进行词向量计算,得到每条新闻文本数据的向量表示。数据处理过程如图7所示。
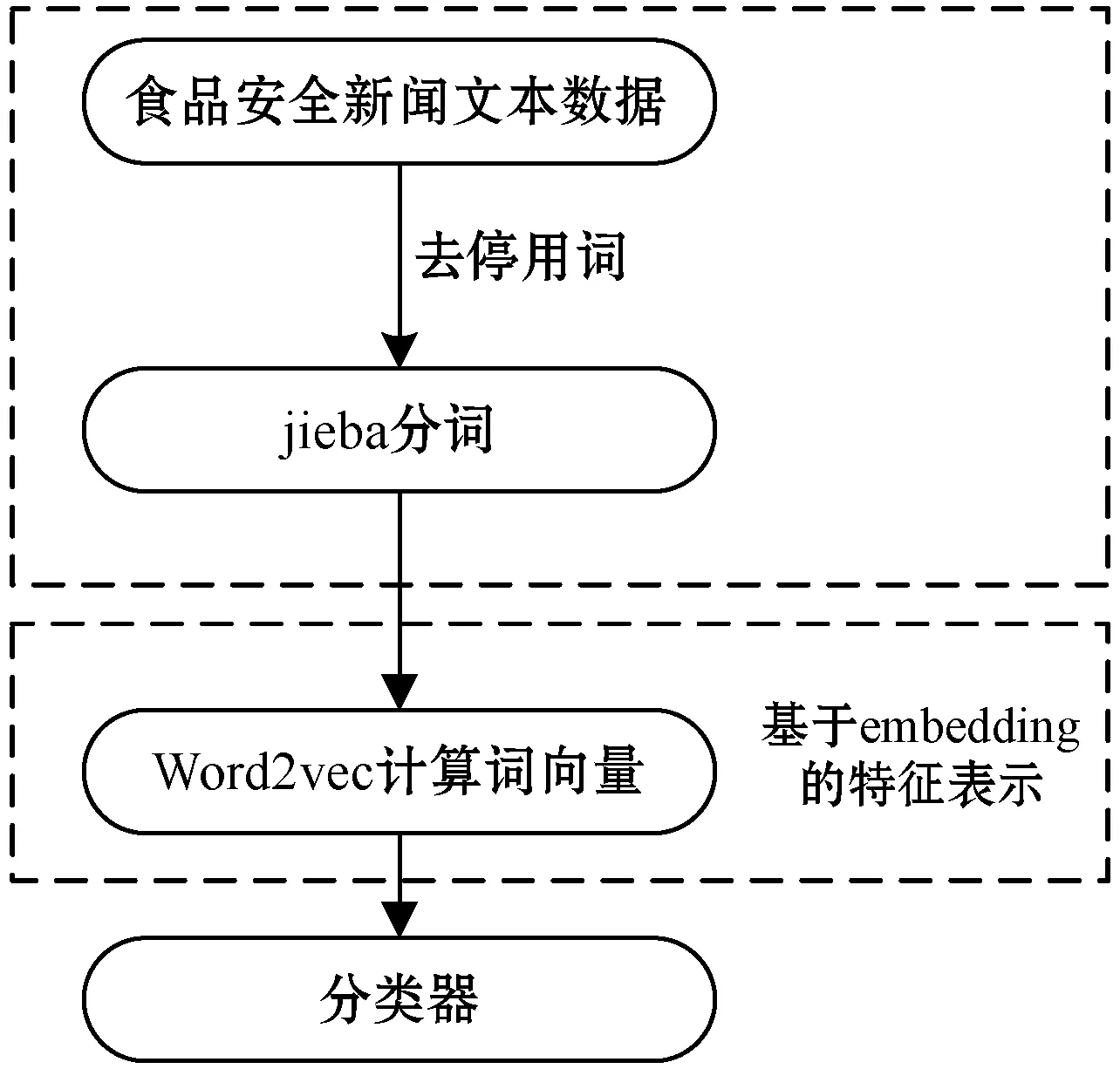
图7 食品安全新闻数据处理
5.2 实验结果及分析
将处理后的食品安全谣言数据分别作为DCS-MI模型、贝叶斯模型及随机森林模型的输入,实验评价指标采用平均F1值和AUC值。图8展示了实验结果。
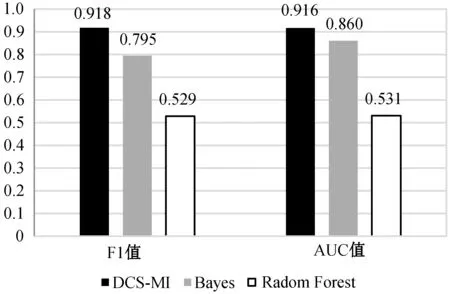
图8 三种算法对食品安全谣言数据分类结果
可以看出,DCS-MI算法对于食品安全谣言数据的分类也取得了0.918 F1值和0.916 AUC值的良好效果。
与贝叶斯模型与随机森林模型对比来看,DCS-MI依然在三个模型中取得了最佳实验结果,随机森林的结果表现最差,即使与表现不错的贝叶斯相比,DCS-MI的AUC值提升了0.056,F1值也有0.123的明显提升,这说明了针对不平衡数据集优化后的DCS-MI算法与传统机器学习算法相比,能够在不平衡数据问题上取得更好的分类表现。
6 结 语
本文提出一种新的动态选择技术DCS-MI,专门用于处理不平衡数据集。DCS-MI使用SMOTE方法对不平衡的训练数据集进行重新采样,并引入了一个新的损失函数来为每个测试实例选择最好的分类器。然后,在4个不同的公共数据集上进行了DCS-MI算法与其他5种算法的对比实验,验证了DCS-MI的优越性能。而后在爬虫获取的食品安全谣言不平衡数据集上使用DCS-MI算法进行实验,并同时使用贝叶斯与随机森林算法进行对比实验,进一步验证了DCS-MI在食品安全谣言识别分类方面应用的有效性及针对不平衡数据集优化的有效性。
未来的研究方向包括:研究不同的重采样方法对DCS-MI的影响,分析基分类器数量对DCS-MI与其他动态选择技术性能差异的影响,使用不同的损失函数选择最佳基分类器。

