基于深度强化学习的路径规划算法研究
曹景祥 刘其成
(烟台大学计算机与控制工程学院 山东 烟台 264000)
0 引 言
随着科技的快速发展和日益普及,机器人、无人驾驶、船只障碍规避、工程机械等都使用了路径规划。因此路径规划受到了许多的关注,越来越多的研究人员对路径规划算法进行改进[1],并且将深度强化学习引入到路径规划中。
深度强化学习(Deep Reinforcement Learning,DRL)结合了深度学习的感知能力和强化学习的决策能力[2]。随着深度强化学习在不同领域的成功应用,使得越来越多的研究人员开始将深度强化学习应用到路径规划[3]。在面对复杂环境和任务时,深度强化学习算法表现突出,有助于提高路径规划的效率[4]。
基于深度强化学习的路径规划算法通过神经网络来选择某一状态的较优动作,根据得到的较优动作组成物体起始位置到目标的较优动作集,最后得到较优路径。所以神经网络的类型和神经网络的参数更新对动作的选择起到了重要的作用[5]。因此本文使用了多层感知机,通过改进的奖励函数使得神经网络参数更加精确,提高神经网络的动作选择效率,最终达到提高路径规划效率的目的。
1 相关工作
过去的许多研究中都是基于已知环境进行路径规划,如文献[6]在已知仓储信息中,提出了基于遗传算法的仓储货位与AGV路径规划协同优化算法,来解决易陷入局部最优的问题。文献[7]使用A*(A-Star)算法进行路径规划要事先存储整个地图,然后依据扩展节点选择当前代价最低的方块进行下一步搜索,直到搜索到终点,从而规划出成本最低的路径。文献[8]提出了机器人避障路径规划的自适应人工势场方法,通过自适应地改变障碍物势场函数的权重,使得机器人逃离局部极小值。在一些领域中,随着路径规划环境信息越来越复杂,存储环境信息对内存的要求过高[9],因此在未知环境中获取较优路径成为研究热点。
由于强化学习不需要先验信息,通过物体和环境不断地交互和试错获取信息,由奖赏机制进行策略优化,是动作到行为映射的学习方式[10],所以强化学习在路径规划中使用越来越广泛。文献[11]将强化学习中Q-learning算法应用到路径规划中,因为无须知道模型就可以保证收敛,在状态空间较小的情况下能够很好地规划路径。文献[12]基于Q-learning算法,提出了一种自适应增强—探索Q学习算法,将探索因子ε的衰减过程分为两个阶段,提高探索效率。文献[13]使用Q学习算法进行路径,将Q学习算法中执行每个动作回报值进行改变,把接收信号的强度作为回报值,大大减少了迭代次数,提高路径规划效率。基于强化学习的路径规划算法适用于低维状态空间[14],因为算法所需数据是通过物体与环境交互获得的,所以当路径规划的环境过于复杂、数据维数过高时,路径规划效率将会下降。
在越来越复杂的实际场景中,需要利用深度学习从大规模数据中提取高级特征。通过深度学习和强化学习相结合,在未知环境中自主学习,并预测出可行路径,以实现自主规划出较优路径,因此深度强化学习被引用到路径规划中。文献[15]将深度Q学习与深度预测网络技术相结合,提出了一种在全局范围内快速实现路径规划的算法,利用时空、天气等道路特征预测未来交通状况,求得全局较优路径。文献[16]提出了一种模糊贝叶斯-深度Q网络算法,对ε-贪婪算法进行修改,将模糊综合评判法和贝叶斯决策算法相结合替代ε-贪婪算法,使探索与利用两种动作选择方式更加高效,生成最优的动作序列决策。文献[17]将深度Q学习算法引入到海战场中进行路径规划,并且将海战场环境网格化,使用卷积神经网络进行路径规划。
研究人员将路径规划的环境信息进行处理,使得环境网格化,环境信息就会相对简单。如果在深度Q网络算法使用卷积神经网络可能会产生过拟合,无法得到较优动作,降低了路径规划效率。在这种背景之下,本文将多层感知机应用到深度Q网络算法中,并将改进奖励的函数运用到神经网络每次更新中,提出一种改进后的深度Q网络路径规划算法。
2 相关知识
2.1 Q学习算法
2.1.1Q值表更新
Q学习算法是一种无模型的强化学习的算法,使用Q值表来存储物体的不同状态s和动作集合A之间的关系。通过物体执行动作a∈A与环境不断地交互,以此达到不同状态之间相互转换的目的,从而不断地更新Q值表,再通过Q值表更新动作选择策略,最终获取最优动作集。因为Q学习式求得全局最优策略,所以Q值表中某时刻信息的更新是通过下一步的状态值函数进行的。比如在t时刻物体选择动作,观察奖励rt进入新状态st+1,并对Q值表进行更新。迭代过程如式(1)所示。
Qnew(st,at)←(1-α)·Q(st,at)+α(rt+
式中:Q(st,at)表示在t时刻时,处于s状态执行动作a的Q值;γ为影响因子;α为学习率。
2.1.2奖励函数
路径规划中的最终目的就是找到长期累积奖励值最大的路径,因此奖励函数有着重要的作用。在Q学习算法中,根据给定的奖励函数判断在某种状态下执行的动作的好坏程度。其中,奖励函数的反馈分为正反馈和负反馈,通过获得的反馈计算下一状态的预期奖励来决定下一步的行动。式(2)为状态-行动-下一状态的预期奖励。
式中:r(s,a,s′)为预期奖励,s为当前状态,a为执行的动作,s′为下一状态;rt+1为下一状态得到的奖励值;R′为奖励空间;p(s′,r|s,a)表示在状态s,执行动作a时,下一状态为s′并且得到奖励值为r的概率;p(s′|s,a)表示在状态s,执行动作a时,下一状态为s′的概率。
2.2 深度Q网络
2.2.1神经网络
深度Q网络[18](DQN)以Q学习算法为核心,将深度学习和Q学习算法融入到一起。Q学习算法中的状态-动作值函数使用神经网络表示,将状态作为神经网络的输入,得到当前状态的每个动作的价值,根据每个动作的价值选择要执行的动作。通过参数为θ的f网络近似代替状态-动作值函数如式(3)所示。
f(s,a,θ)≈Q(s,a)
(3)
式中:f可以是任意类型的函数;s为状态;θ为网络参数;a为动作;通过函数来近似代替Q值表,减少了内存的使用。
在深度Q网络中存在两个结构相同但参数不同的神经网络,分别为预测网络Qe和目标网络Qt。预测网络会通过时序差分法的误差不断更新,计算出Qe估计值,目标网络则是计算Qt现实值。目标网络每隔一段时间获取预测网络参数进行更新,降低了当前Qe值和目标Qt值之间的相关性,避免神经网络的训练参数陷入到局部最优解中。
2.2.2记忆回放机制
在最初的深度强化学习中,神经网络根据输入的状态得到每个动作的Q值,选择这些Q值中最大的一个。但是这些训练样本都是通过前一个状态得到的,因此各个状态之间有着明显的关联性。后来Google的DeepMind团队在学习过程中加入了记忆回放(Memory Replay)机制[19],通过从经验池中随机获得训练样本,降低样本之间的相关性,打破了陷入局部最优解的可能,使得学习到的策略趋向平稳。也正是因为记忆回放机制才使得深度学习顺利地应用于强化学习。
3 改进DQN的路径规划算法
3.1 DQN算法设计
随着研究人员将路径规划的环境信息进行处理,使得环境网格化,如果在深度Q网络算法使用卷积神经网络可能会产生过拟合,在这种背景之下,本文将多层感知机使用到深度Q网络算法中,将改进奖励函数运用到神经网络每次更新中,提出一种改进后的深度Q网络路径规划算法。
3.1.1多层感知机
在多层感知机(Multilayer Perceptron,MLP)中除了输入层和输出层,中间可以有多个隐层。如图1所示,MLP含有n个输入神经元代表输入n维的数据,m个输出神经元代表输出的类别为m种,中间含有一个隐藏层,隐藏层的神经元越多代表模型的拟合能力越强。

图1 多层感知机结构
图1中,x为输入数据,y为输出在模型训练的过程中以最小化分类误差为目标函数。使用反向梯度传播算法对模型进行训练,训练完成后得到使样本分类误差最小的一组参数w进行前向传播得到结果y。单层感知机如式(4)所示。
式中:i为上一层神经元的下标;j为当前层神经元的下标;wij为神经元j的权重。
根据多层感知机可得出DQN算法的两个网络的网络结构图并且两个网络相同,如图2所示,其中:k表示动作的个数;n和m表示不同网络层的神经元个数。

图2 网络结构
预测网络输入是从经验池中获得的数据(s,a),状态s为物体位置(x,y)。由三层全连接层计算当物体处于状态s时执行a动作所获得的奖励。目标网络的输入是从经验池中获取的数据(s′,r),r表示为状态为s执行动作为a时获得的奖励,将处于s′状态下获得的奖励与r相加得到两个动作的奖励。
3.1.2奖励函数
在现有的奖励函数中,当物体处于探索路径状态时,不同动作可能返回相同的固定奖励值,然而不同动作的相同奖励值与较优的动作选择关联性较小,导致更新后的神经网络与较优动作-状态值函数拟合较低。因此本文将三次函数引用到奖励函数中,根据不同动作返回不同奖励值,将不同的奖励值应用到神经网络的更新中,使得更新后的神经网络与较优的动作-状态值函数更加拟合。因此本文设置了以目标位置为中心的范数约束如式(5)所示。

式中:p为物体位置;t为目标位置;d为约束距离。
通过范数约束设置奖励函数,返回物体处于某个状态的奖励值,如式(6)所示。当物体处于探索路径状态时,通过式(5)获得参数l、h。
R=l×(x-h)3
(6)
式中:参数l确定函数的单调性,并决定图像的趋向于对称中心的速度;参数h是X轴的截距;当物体处于探索路径状态而不是终止或寻找到目标状态时,x为当前时刻物体到目标之间的欧氏距离;R为物体执行动作后的奖励值。
根据物体状态是否满足式(5),使用式(6)计算执行某动作返回的奖励值为正奖励或负奖励。不同状态的奖励值如表1所示,其中,Value1和Value2分别为设置的到达目标状态和撞到障碍物状态时返回的奖励值。

表1 奖励表
将R设为奖励函数,在状态s下根据表1所获得的奖励期望如下:
Rs=E[Rt+1|s=st]
(7)
式中:E为期望;Rs是处在t时刻的状态s的下一个时刻所获得的奖励期望。因此当前状态的动作价值如式(8)所示。
式中:Rt+i为在t+i时刻获得的奖励值。
3.1.3动作选择机制
动作选择通常会有两种方式,分别为Exploration(探索)和Exploitation(利用)。为了平衡两种动作选择方式使用了ε-贪心算法,该算法采用了ε概率选择较优动作,在1-ε概率内选择随机探索。而本文使动作选择概率ε随着训练步数线性增加,通过线性增加ε-动作选择概率来解决训练后期存在的过度探索错过较优路径的问题。
3.2 模型训练
在模型训练的每一次迭代中DQN网络参数更新是从经验池中随机取出一批数据。将这些数据传入到两个网络中,在两个网络所得到的值的基础上通过对损失函数梯度下降实现的,损失函数如式(9)所示。
L(θ)=E[(Qt-Qe(s,a,θ))2]
(9)
然后对得到的损失函数求梯度,如式(10)所示。

执行N步后,将预测网络的参数覆盖目标网络的参数。其中经验池中的数据是通过物体不断与环境交互获得的信息(s,a,R,s′)。
通过对损失函数进行梯度下降实现预测网络的更新如式(11)所示。
式中:η为梯度下降的学习率;θi为上一次的网络参数。
图3为DQN更新流程,将当前的环境状态输入给预测网络,然后由预测网络通过动作选择机制与环境进行交互,会得到该动作奖励和下一步状态。将此四元组存入到回放记忆单元,当记忆回放单元的记录满足随机存取记忆回放单元记录个数时,从中随机取得一小批量样本并进行训练。每个N时间步后预测网络会将函数拷贝给目标网络,最后根据损失函数进行预测网络的参数更新。
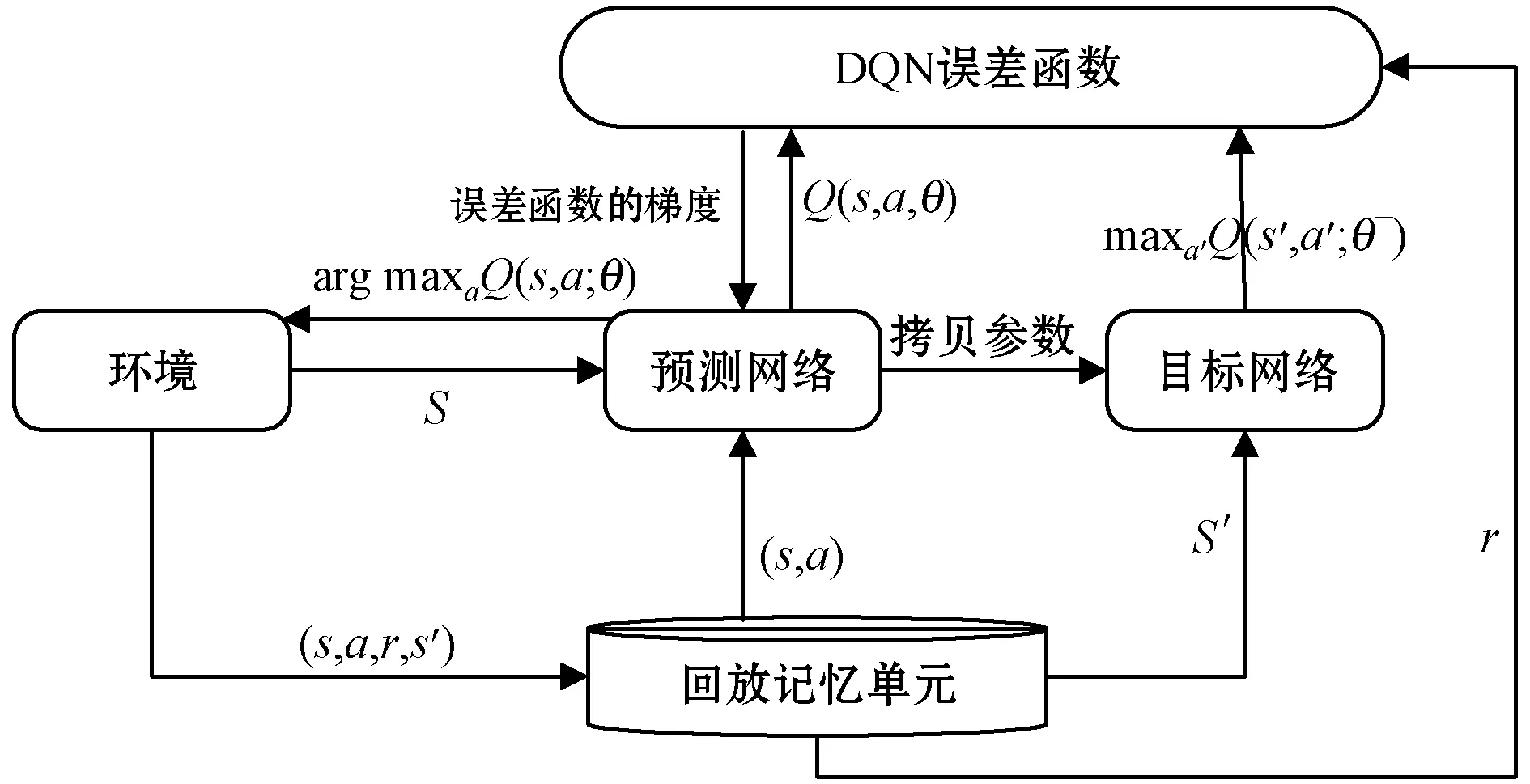
图3 DQN更新流程
通过图3可得改进的DQN算法的路径规划的伪代码,如算法1所示。
算法1基于DQN的路径规划算入:物体的状态s。
输出:目标网络参数。
初始化经验池D
初始化目标网络Qt和预测网络Qe参数,网络参数均服从与期望为0、标准差为0.2的高斯分布,未撞到障碍物的奖励为0 for episode=1 tokdo
初始化物体位置
While True:
利用ε贪婪策略选择状态动作:
执行动作at后得到下一个状态st+1
If rect=target:
未撞到障碍物的奖励为式(6)
通过表1得到的即时回报Rt
将(st,at,Rt,st+1)放入经验池D
if rect=block or rect=target
break;
随机从经验池D中采集一组数据(sj,aj,Rj,sj+1)
设定
利用式(9)对Qe(s,a;θ)和yi求损失函数L根据公式(11)对L进行梯度下降,实现网络的更新
ε←ε+0.000 01
式中:rect表示物体当前的位置;block代表障碍物的位置;target表示物体目标的位置。
4 实验仿真与分析
4.1 实验场景
通过将文献[17]的实际环境网格化进行实验,如图4所示,将不同的网格连接,以此来模拟不同大小的长方形障碍物,总共有八个障碍。正方形为起点,即物体所在位置;圆形为追逐目标,即目标位置。最后结果获得的路径为从起点躲避所有障碍物到达终点的最短路径。
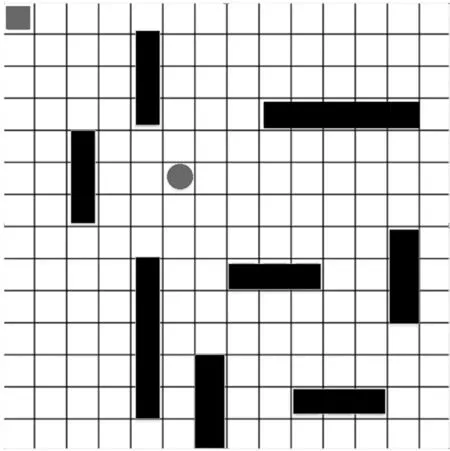
图4 仿真环境
4.2 实验参数
在实验中,仿真环境中每个网格边长为1,网格的对角线长度为21/2。通过前期获得训练获得目标位置计算范数约束距离d,将(0,d)作为式(6)的零点,则d=l×(0-h)3。设置物体在目标四周距离为0时,状态的奖励值为15,代入式(6)中,得到0=l×(15-h)。由此可得l=-0.2,h=4.24,则奖励值表示如式(12)所示。
r=-0.2×(x-4.24)3
(12)
因为路径规划的最重要目的就是找到最大的奖励值,从而找到目标。为了和其他状况有较大的区分,到达目标的奖励为50。而撞到障碍物要比其他状况获得的奖励值要小,奖励值为-5。当物体处于探索路径状态时,在没有发现目标阶段则奖励值为0,当发现目标之后奖励值通过式(12)获得,因此不同状态的奖励值如表2所示。
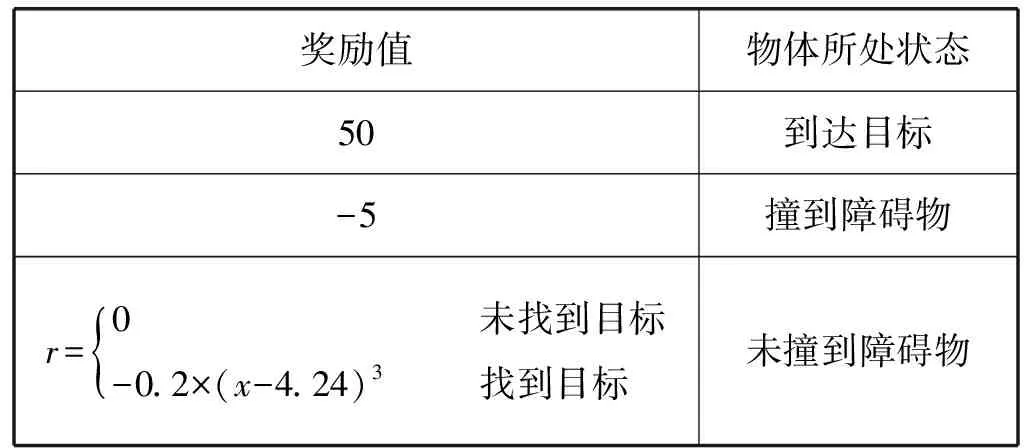
表2 确定参数的奖励表
在多层感知机中,如果网络参数数量过大会出现动作价值的过拟合,如果较小会出现动作价值的欠拟合。为了更好地训练网络,将网络参数的个数设为15。
4.3 实验结果
在上述实际场景,基于仿真环境进行实验,每200次进行目标网络的参数更新。开始训练时,因为经验池没有记录,所以开始的前400次训练在不断地探索,积累一些记录并将这些记录进行存储。因为随机取出记录的个数为100,将训练设置400后可以将样本的相关性降得更低,当400次训练结束后,开始通过随机取出经验池中的记录进行网络的训练,使用梯度下降算法更新网络的参数。刚开始时因为经验池里面没有记录,无法取出进行训练,所以开始的路径会出现各种碰撞障碍物的情况,无法找出最优路径。如图5所示。

图5 初始路径寻找
而随着训练次数的提升,经验池里面的记录增加,网络参数的更新,并且ε-贪心算法中的ε=0.9也会以0.000 01的速度随着路径探索而慢慢增加,ε的上限为0.999 9,以此将动作选择慢慢趋向于利用方式,但不会完全使用利用方式。因此使得路径的选择就会越来越好,最后获得最优路径,如图6所示。
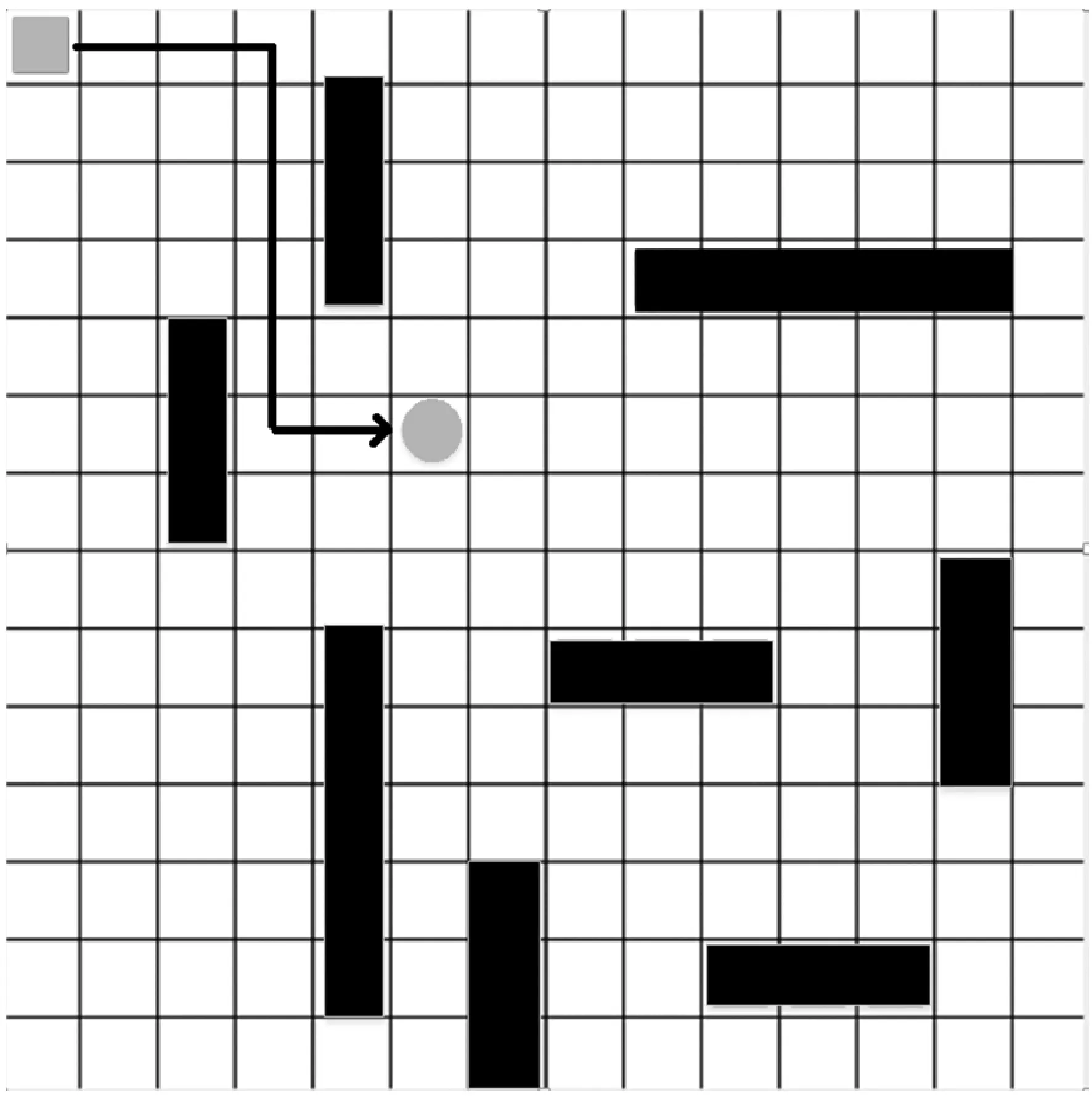
图6 最优路径
本文与DQN算法和Action-critic算法进行比较,当物体训练1 000轮时三种算法的不同奖励值如图7-图9所示。图7为本文算法的奖励值,开始训练的前400步,因为是随机探索的,没有根据在经验池里的记录更新网络参数,所以奖励值会比较乱。而随着前300次的训练结束,经验池有充足的经验,则可以来进行参数更新。随着训练次数的增加,ε越来越大,动作选择越来越趋向于某个状态的最大奖励的动作,奖励值也就变得平稳。图8和图9分别表示普通DQN算法和Action-critic算法的奖励值。

图7 本文算法1 000步奖励值

图8 DQN算法1 000步奖励值
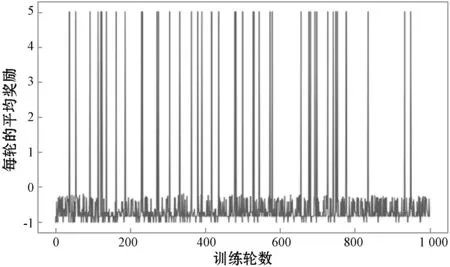
图9 Action-critic算法1 000步奖励值
本文选取探索规划轮数为评价指标,将DQN算法和Action-critic算法作为对照算法,比较了三个算法的总规划步数,如图10所示。

图10 总规划轮数
观察图10可以发现在达到相同的效果目的下,本文的总探索规划步数比其他两种算法明显减少,表明本文算法有更好的路径规划和规避障碍的能力。
5 结 语
本文提出一种基于深度Q网络的路径规划算法,该算法可以帮助物体进行路径规划、障碍规避和目标跟踪。与基于DQN和基于Action-critic的路径规划算法相比,实验结果表明本文算法与其他方法在相同环境下,总探索步数更少,寻找最佳路径速度更快。因此,本文方法在路径规划方面具有更快的规避障碍的能力和跟踪速度。

