基于信道状态信息的室内人数统计算法

史文华 戴 欢 周泽仑 蒋敬敬

(苏州科技大学电子与信息工程学院 江苏 苏州 215000)

0 引 言

许多场景对人员数量都有应用需求，比如：车站根据人群密度对客流进行疏导，在保障公共安全的同时，提高出行效率[1]；智能家居系统根据室内人数的多少自动调节电器的功率，实现节能的目的[2]；商场根据各个区域人数的分布来分析消费者的消费习惯，从而及时调整销售策略[3]。目前人数统计的方法可大致分为基于图像的人数统计方法和基于可携带设备的人数统计方法两大类。

基于图像的人数统计方法较为传统，主要依靠计算机视觉技术。Pore等[4]提出一种应用方向梯度直方图找到人员目标，再根据卡尔曼信道生成人的运动轨迹，在轨迹进出口方向计算人员数量的方法。Sam等[5]提出了Switch-CNN网络，利用图像中人群密度的变化来提高预测人群数量的准确性。Shani等[6]利用卷积神经网络在密集人群中进行稀疏头部检测，通过支持向量机对分割的图像进行分类，再计算每个人群斑块的人数完成人员计数。这类方法大多使用摄像头获取图像信息，在复杂环境中易被物体遮挡，存在视觉盲区，同时受限于光学传感器的特性，受光线影响较大，只有在光线充足的条件下才能有较好的效果。

基于可携带设备的人数统计方法主要依靠智能手机和电子标签等设备实现人数统计。Kannan等[7]通过在室内人员的智能手机上安装一款软件，利用手机麦克风发出特定频率的音频信号，并用手机听筒接收这些信号，对其进行分析处理，求出手机数量，依此估计出人员数量。Weppner等[8]提出基于iBeacon技术的方法，利用智能手机作为被检测设备进行人数估计，融合不同设备的蓝牙数据，将精确度提高到了75%。Ding等[9]使用RFID标签进行区域内的人数统计工作，人数越多，标签反向散射射频信号的信号强度值的变化就越大，通过分析接收到的射频信号估计出人员数量。这类基于设备的人数统计方法往往需要人员携带特定的设备，便利性差，且成本过高。

随着Wi-Fi的普及，基于Wi-Fi进行人数统计的方法成为新的突破口，得到了学术界的广泛关注。Seifeldin等[10]提出了Nuzzer系统，该系统利用RSSI的方差来计算人数。然而，由于RSSI无法刻画多径传播，易受环境因素影响，在复杂环境下计算人数的准确度不高。Xi等[11]提出了FCC系统，该系统分析了人数与CSI变化之间的关系，并提出了膨胀后的CSI矩阵中非零元素百分比的度量标准，依据灰色模型理论[12]对多种人数情况下的非零元素百分比序列进行拟合得到增长曲线，之后计算出人数。Domenico等[13]提出了Trained-once Crowd Counting系统，其利用CSI幅度的特征差数据，通过最小化测试样本与训练样本指数来计算人员数量。Zou等[14]提出FreeCount系统，该系统依据信息论进行特征选择，选择出最能代表人体运动敏感的特征，针对时间和环境差异建立具有鲁棒性的分类器，最后求出区域内人员的数量。

本文提出一种基于信道状态信息的室内人数统计方法。该方法首先从CSI原始数据中求出相位和幅度，使用解卷相位与线性变换的方法实现相位校正，减小因收发端时钟不同步引起的频率偏差和时延，使得相位能以簇的形式集中[15]。采用Hampel滤波器分别对CSI数据的幅度和矫正后的相位进行异常值检测处理，滤除信号衰落和多径效应引入的直流分量和噪声，并采用PCA对去噪后的数据进行降维处理，提取出有效的特征，最后利用基于单层决策树的AdaBoost算法训练分类器进行分类，统计出室内人员数量。

1 信道状态信息

无线信号在传播过程中会产生多径效应，造成信号衰落和相位移动。正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是一种多载波调制技术，能有效减弱多径效应，其原理是将高速串行数据信号划分成若干并行的低速数据流，并将信道划分为若干个子信道，各个子载波相互正交。对于每一条子载波，可以使用CSI来描述无线信道的散射、衰落和功率衰减情况。在窄带平坦衰落信道中，信道状态的频域模型可以表示为：

Y=HX+N

(1)

式中：X和Y分别是发射端和接收端信号向量；H是一个对角矩阵，为信道状态信息矩阵；N为噪声向量。对于包含K个子载波的CSI，其矩阵表示为：

H=diag(h1,h2,…,hK)

(2)

式中：K=114。每个子载波hk为复数形式，也可以表示为幅度和相位的形式：

hk=realk+j×imagk=|hk|ej∠hk

(3)

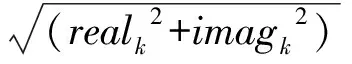
2 基于信道状态信息的人数统计方法

图1为不同人数情况下CSI幅度的方差，当仅有1人时，CSI幅度的方差和其波动范围都很小；当人数增加到3时，CSI幅度的方差和其波动范围都变大；当人数为5时，CSI幅度的方差变得更大，且方差波动范围更大。

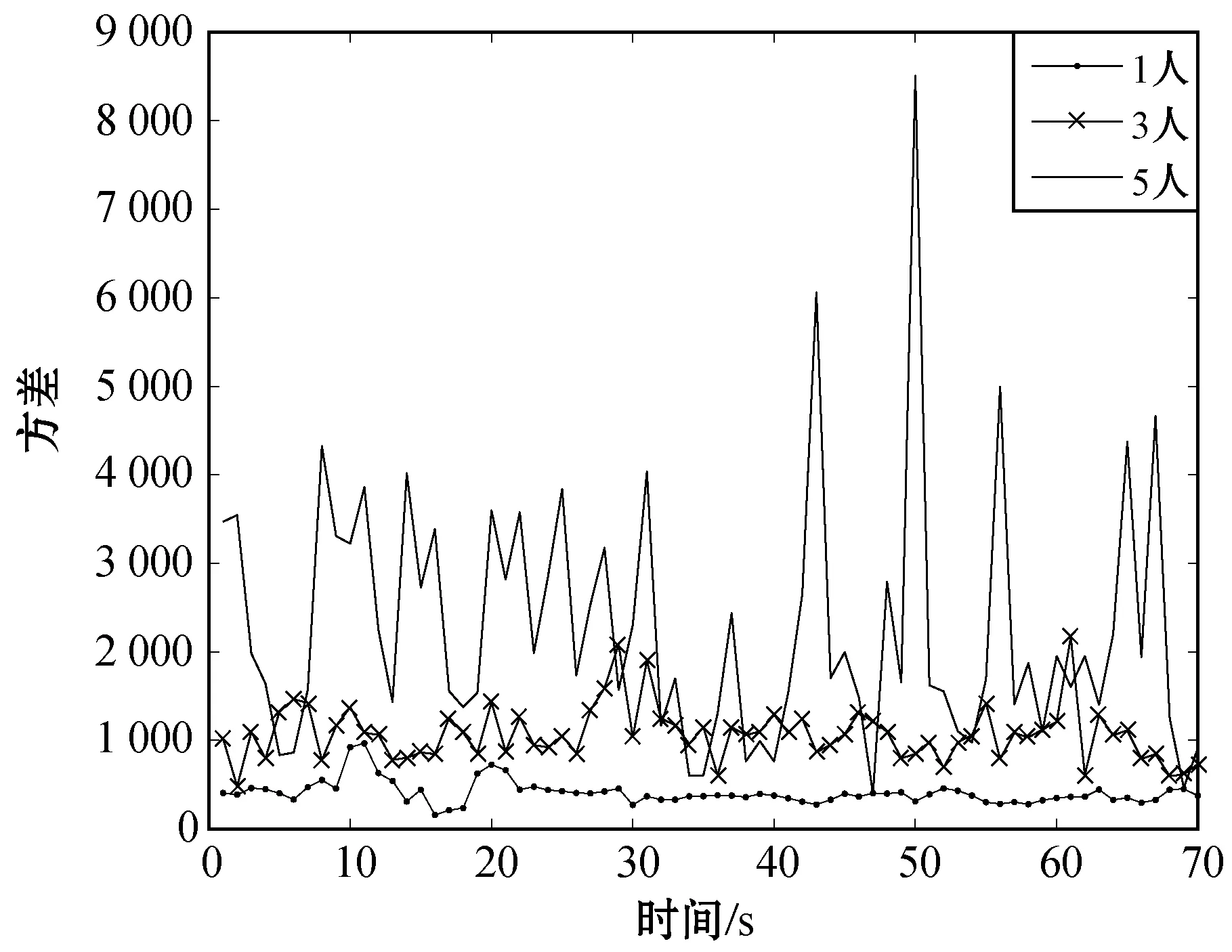
图1 不同人数情况下CSI幅度方差

如图2所示，(a)、(b)和(c)分别为场景中有1人、3人和5人的情况下，经矫正后的CSI相位的分布情况。可以看出，随着人数增多，相位的波动和离散程度变大，且分布在(π,2π)上的数据变多。

(a) 1人情况下CSI相位

(b) 3人情况下CSI相位

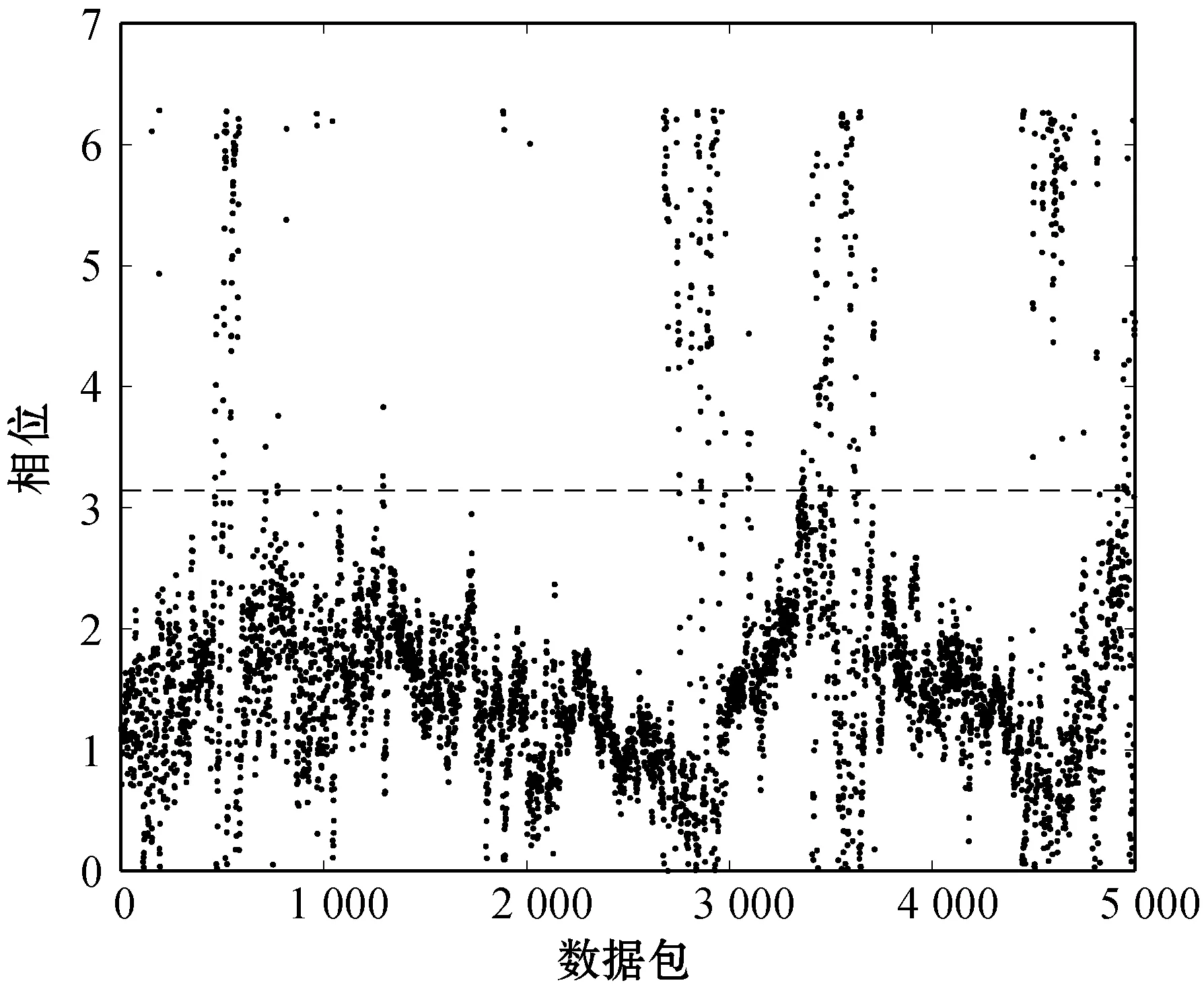
(c) 5人情况下CSI相位图2 不同人数情况下CSI相位分布

由此可见，区域内活动人数不同对CSI的影响也会不同。若场景中仅有一人，环境相对稳定，CSI数据的波动和离散程度较小；当人数增多时，CSI数据会发生更加明显的波动。CSI包含幅度和相位信息，本文旨在探究随着区域内人数的变化，CSI幅度和相位的变化情况，并以此为依据进行分类，统计出人员数量。

如图3所示，本文方法主要分为四个步骤：首先进行数据采集，通过Wi-Fi设备获取监测环境内的CSI数据；其次对数据进行预处理，先对CSI相位信息进行矫正，再对CSI幅度和矫正后的相位进行Hampel滤波，去除异常值；然后进行特征提取，分别对去除异常值后的幅度和相位进行主成分分析，提取出属性特征；最后，基于属性特征构建人数统计模型。

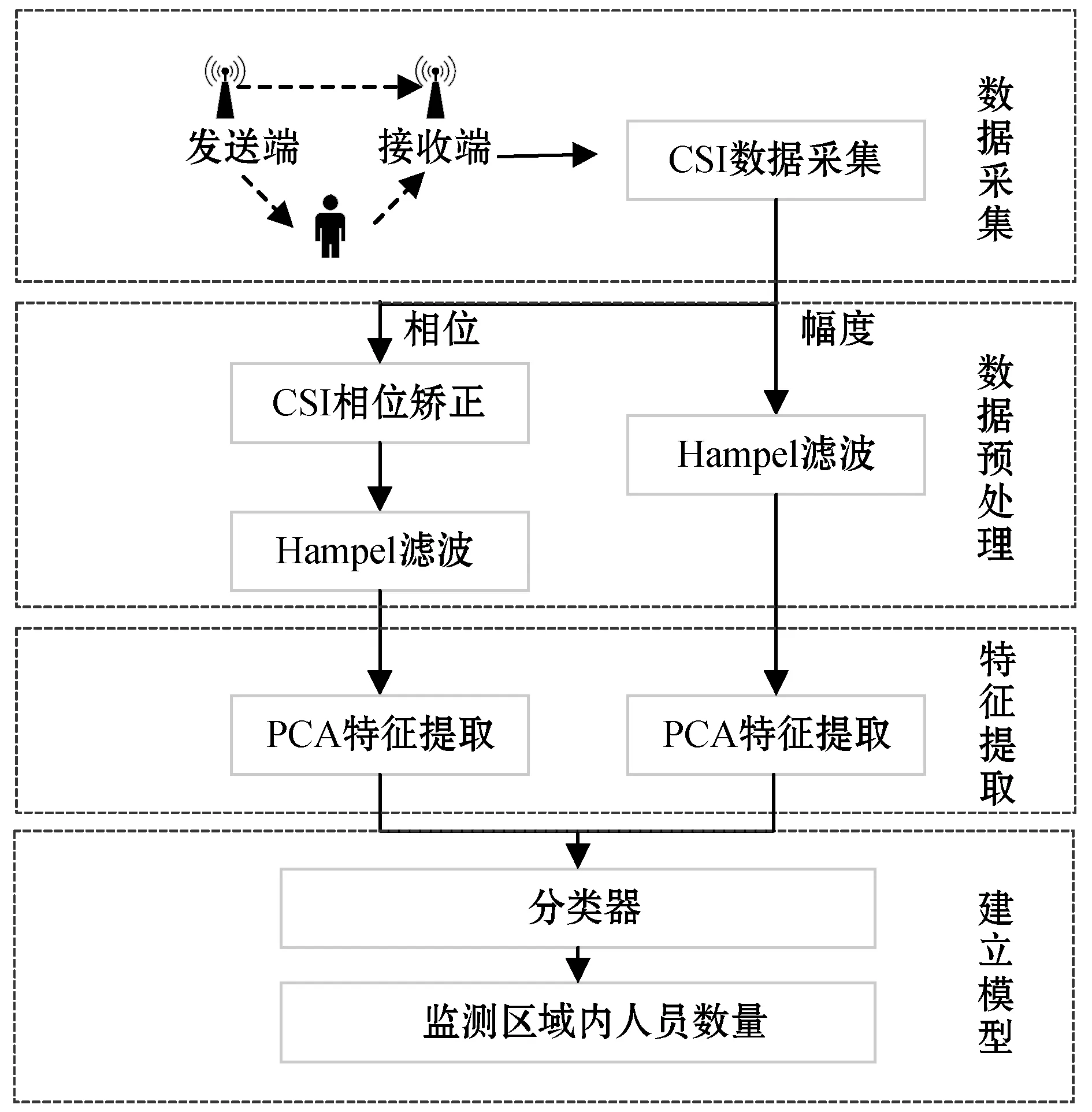
图3 本文方法架构

2.1 CSI相位矫正

由于采集到的原始CSI数据存在采样频率偏移、包边界检测误差等问题[16-17]，导致CSI的相位发生极大误差，其值随机分布在(-π，π)之间，如图4所示，杂乱的分布无法反映周围环境的变化。本文采用相位解卷和线性变换的算法重构原始CSI数据，在尽可能保留有效信息的前提下获取到规则的相位信息。第i个子载波的相位可表示为：

式中：∠hi表示原始相位信息；ki表示第i个子载波的索引；δ表示接收端的定时偏移；N为快速傅里叶变换采样数；β为未知的恒定相位偏移；Zi为测量噪声。Zi是设备固有的测量误差，且值较小，可忽略不计。由于δ和β的值无法确切得知，需要通过线性变换的方法消除。定义a和b两个线性相关项，a为接收响应的相位的斜率，b为偏移量。

经过线性处理后的相位比原始相位更加稳定，有序分布的数据能够反映出周围环境的信息。图5为经过本方法重构后的CSI相位分布，与图4相比，数据的分布不再杂乱无章，主要集中在(0,π)之间，并且有一定的规律性。

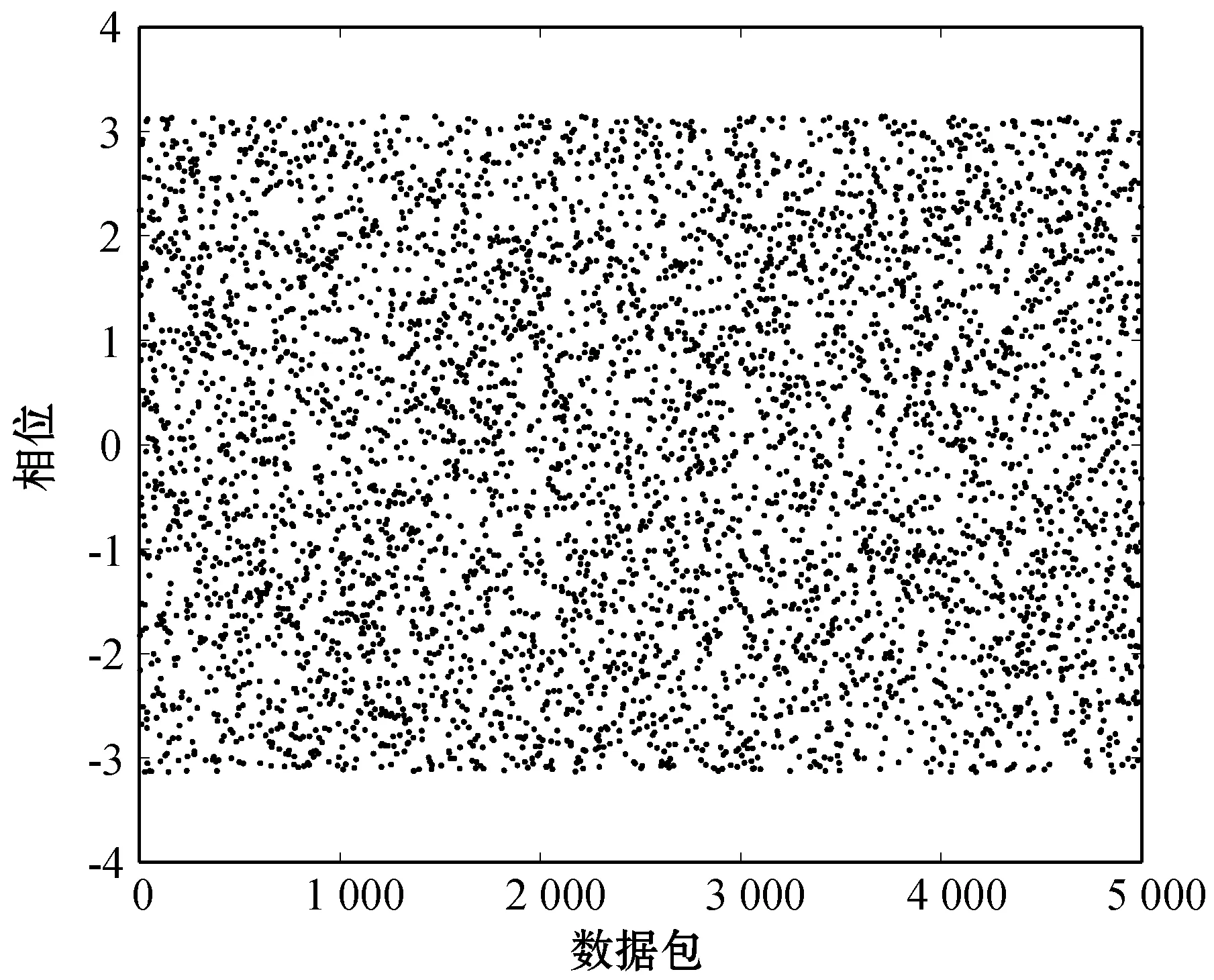
图4 原始CSI相位分布

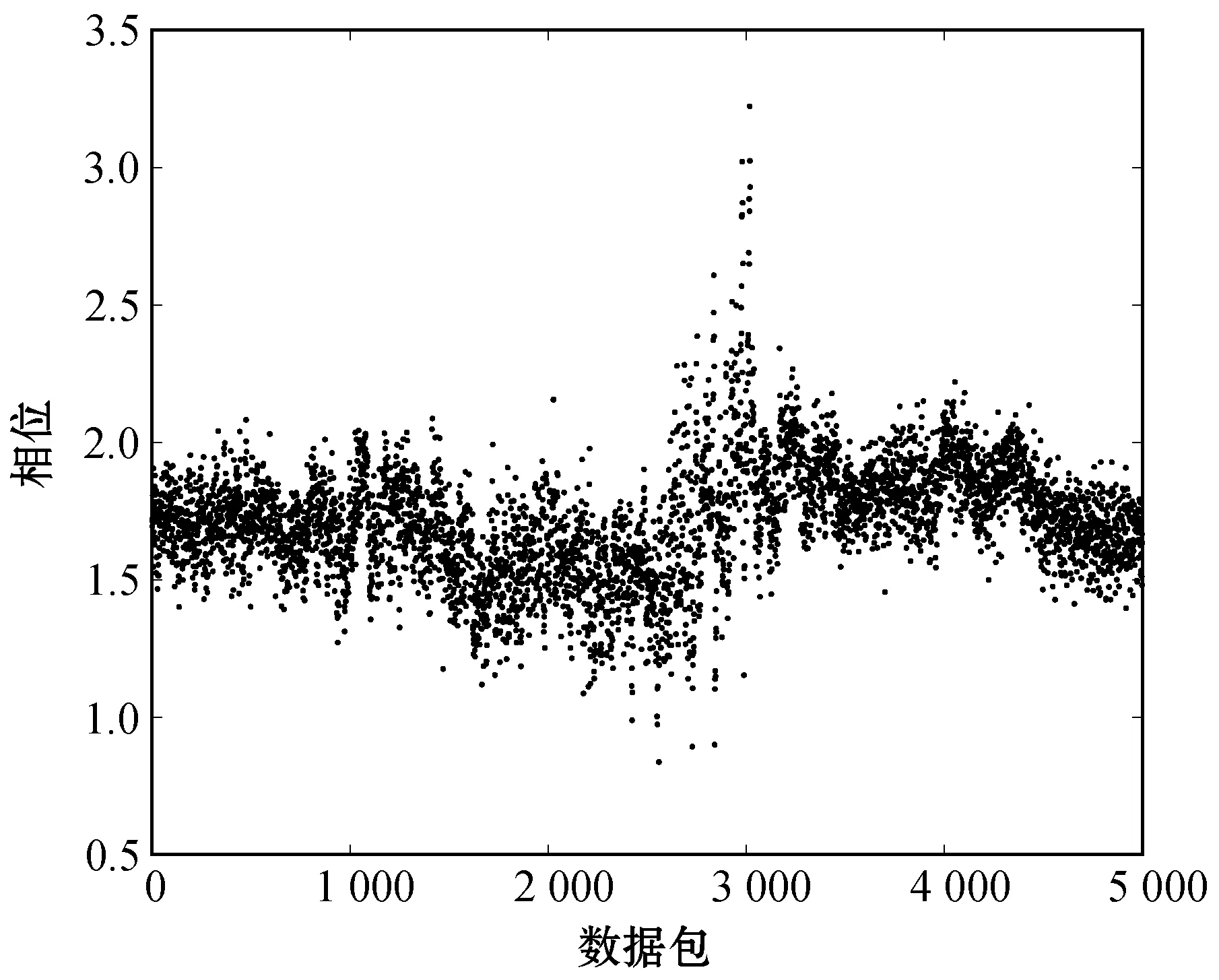
图5 矫正后CSI相位分布

2.2 Hampel滤波

CSI具有很强的敏感性，易受环境影响产生大量噪声。Hampel滤波器能有效检测和去除数据中的异常值，其基本思想是加权滑动平均。对于一组数据X，首先计算出这组数据的中值Median，求出每一个数据与Median的差值，并取绝对值得到序列Y。然后计算出其中值M，这个值反映了数据分布的离散程度，被称为绝对中位差，其计算公式如下：

M=median(Xi-Median)

(7)

可求出测量值的分数，其公式如下：

式中：常数0.674 5保证M的期望值等于正态分布数据的标准差。设定阈值t，当Zi>t时，则认定该测量值为异常值。

Hampel滤波器不直接求出方差，而是用绝对中位差作为方差的近似估计，其对极端的异常值不敏感，并且不要求数据正态分布，能起到良好的检测和去除异常值的效果。图6和图7分别为CSI幅度经过Hampel滤波前后的对比。

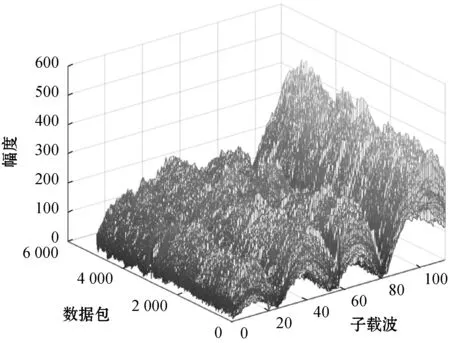
图6 原始CSI幅度

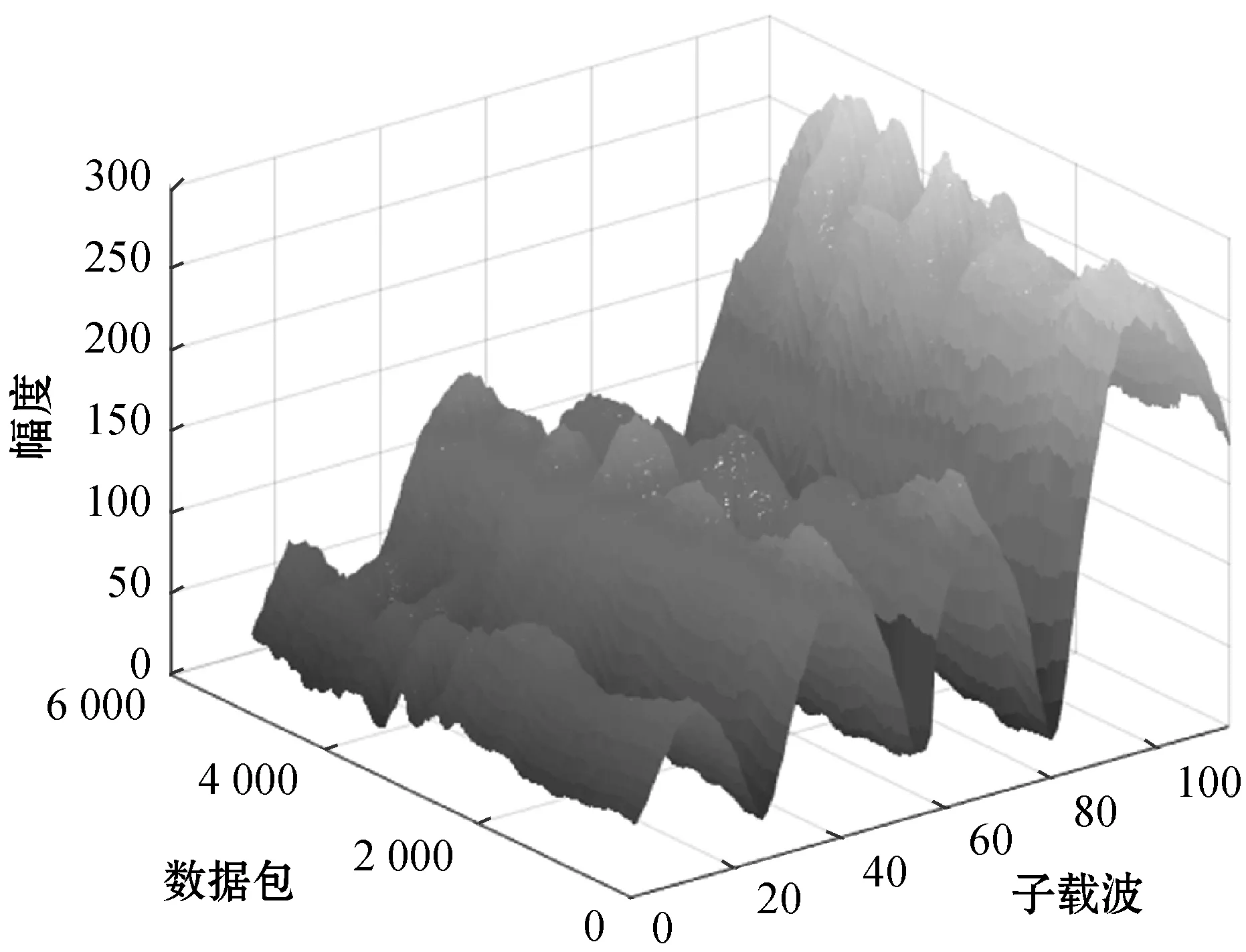
图7 滤波后CSI幅度

2.3 PCA特征提取

由于本文实验所用设备的每个天线对之间存在114个子载波，即3×3×114个子载波，再将CSI数据分解成相位和幅度后，数据维度较高，本文使用PCA算法对预处理后的数据进行降维，在保证信息损失最小化的同时降低了数据的维度。通过计算得到特征值在总数中所占比例，可知该维度的信息量，依此来选择合适的维度作为分类时的属性特征。

PCA的基本思想是从原有特征中计算出一组按照重要性从大到小顺序排列的新特征，新特征是原有特征的线性组合，互不相关。原有特征在新特征上的映射值成为降维后的新样本。PCA的实现流程如下：

输入：X=(x1,x2,…,xn)，n个p维的列向量。

输出：降维后的样本集X′。

1.对所有样本进行中心化。

2.计算样本的协方差矩阵XXT。

3.对协方差矩阵XXT进行特征分解，得到特征值。

4.选取按降序排列的前k个特征值所对应的特征向量w1,w2,…,wk。

5.将原样本投影到新的特征空间，得到新的降维样本，X′=X×W，W=[w1,w2,…,wk]，其中：X为n×p维；W为p×k维。

2.4 人数统计

在进行人数统计时，分为离线和在线两个阶段。离线阶段将不同人数条件下所采集数据的属性特征代入分类算法中进行训练，因这些属性特征之间具有较大的差异，能被有效地区分出来，最终可训练出有效的分类器。在线阶段对当前的数据进行同样的预处理和特征提取，使用训练好的分类器便可统计出当前区域内的人数。本文选取了SVM、KNN、ANN神经网络和基于单层决策树的AdaBoost算法进行对比实验，选出准确率最高的一种作为最终的分类算法，具体如图8所示。

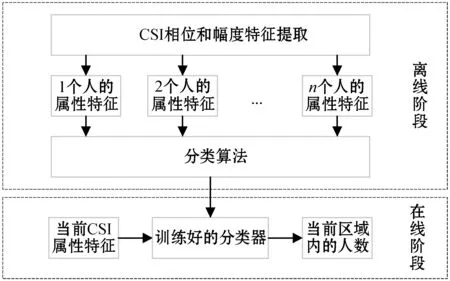
图8 分类架构

3 实 验

3.1 实验设置

本文所使用的设备为图9所示的3×3天线的TP-link 4900v2无线路由器，共使用两台，各作为发射端和接收端。为了获取更详细的信道状态信息，我们升级了Atheros CSI工具，开发了一个新的基于OpenWrt的固件，可以直接从无线路由器上采集CSI数据，每个天线对包含114个子载波，信号频率可设置为5 GHz，带宽为40 MHz。实验环境为7 m×10 m的实验室。实验如图10所示，在实验室一端部署两台路由器，分别采集1人至5人在静止和随机运动两种情况下的CSI数据。

图9 硬件设备

3.2 实验结果与分析

本次实验采集1人至5人随机运动情况下的CSI数据各5 000条，共25 000条数据作为原始数据集，其中每条数据包含3×3×114个数据值。经过数据预处理和降维后，每条数据包含20维相位数据和34维幅度数据，形成最终的数据集。数据训练时分别在每种情况的数据中选取1 000、1 500、2 000、2 500和3 000条数据作为训练样本，其余作为测试样本。

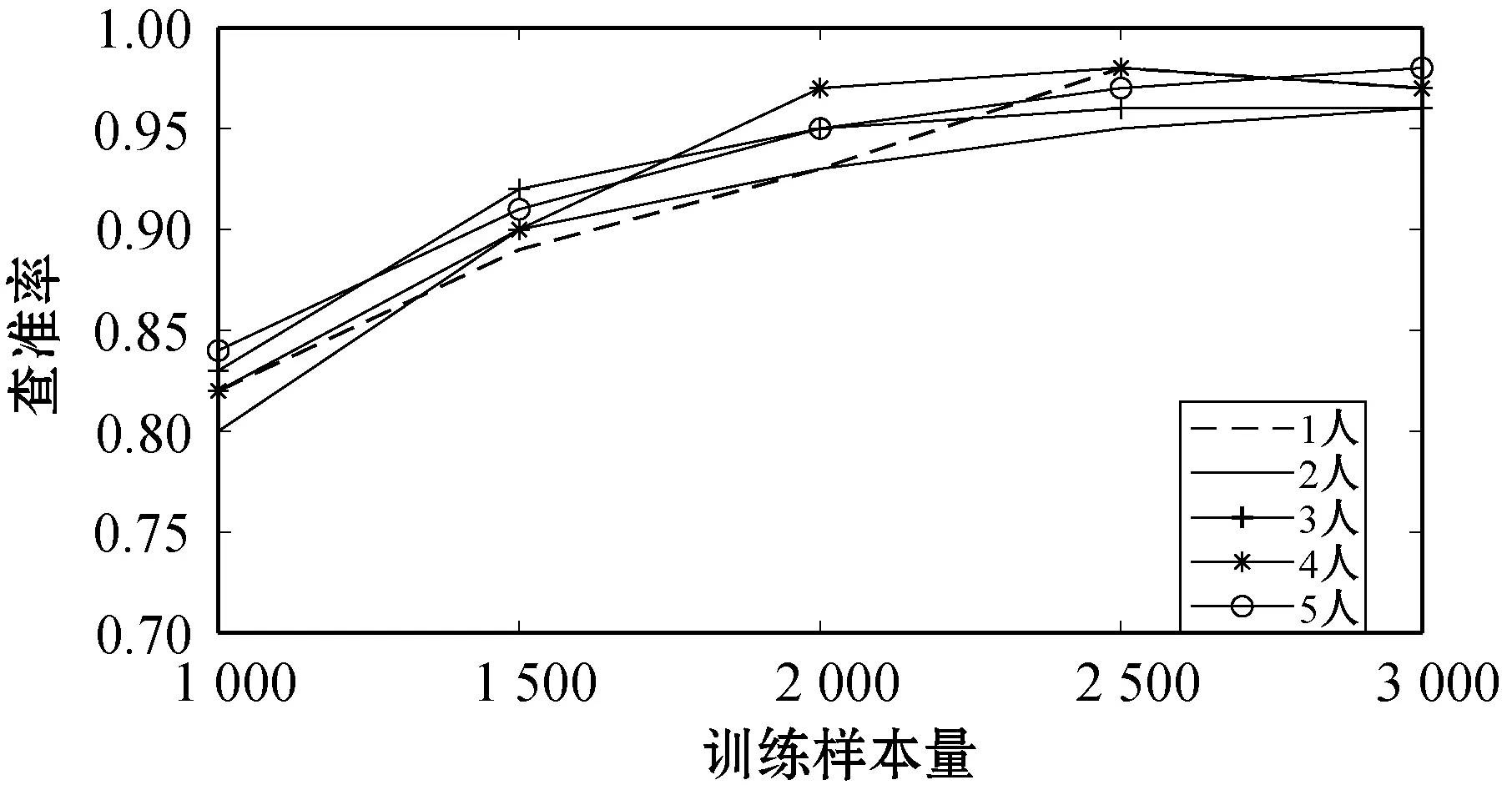
图11为四种分类算法在不同训练样本量时的查准率，可以看出，基于单层决策树的AdaBoost算法具有更好的分类效果，因此选用其作为最终的分类算法。AdaBoost算法的工作机制是先依照初始权重从训练样本中训练出一个弱学习器，再根据其表现调整训练样本的分布，使得错误的样本在之后获得更大的权重，接下来依照新的权重训练下一个弱学习器，重复以上操作，直到学习器数目达到指定值T，将这T个弱学习器通过加权结合，得到最终的强学习器。

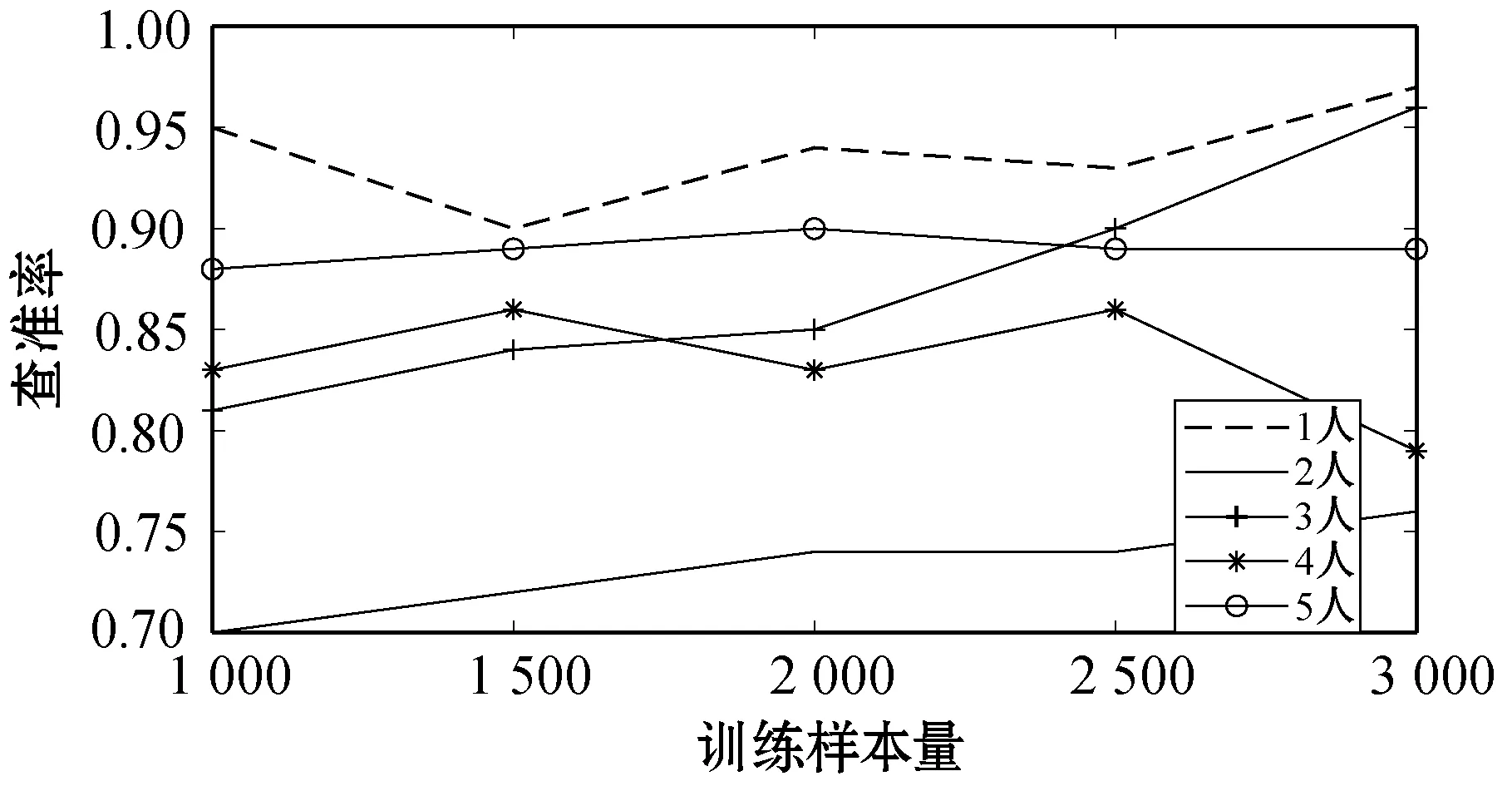
(a) ANN神经网络

(b) KNN

(c) SVM

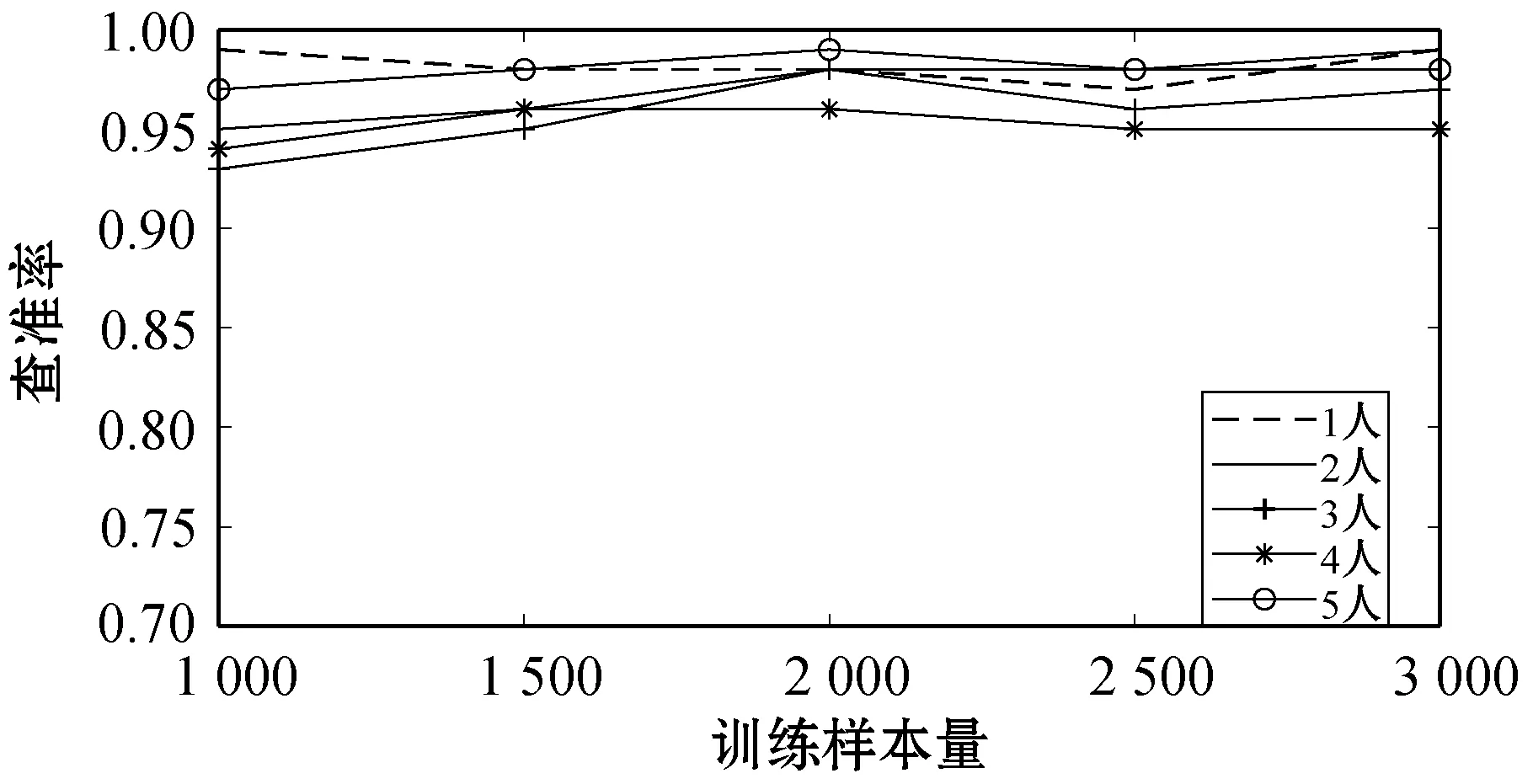
(d) 基于单层决策树的AdaBoost算法图11 四种算法在不同训练样本量下的查准率

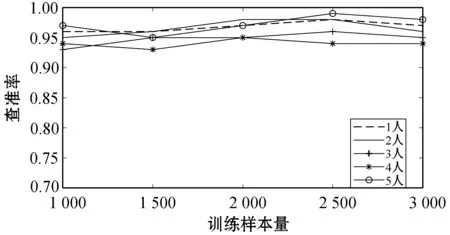
图12和图13分别展示了在人员静止和随机运动两种情况下，本文方法对于人数识别的准确率。人员静止时，环境相对简单，CSI仅受人体呼吸和心跳等生理活动影响，所以识别率很高；人员随机运动时会造成环境中存在一些不确定因素，导致识别率降低。尽管在人员随机运动的情况下，环境比较复杂，但本文方法的准确率仍然达到96.4%，而在人员静止时，准确率更是高达99.2%，说明本文方法切实可行，且具有很高的可靠性。

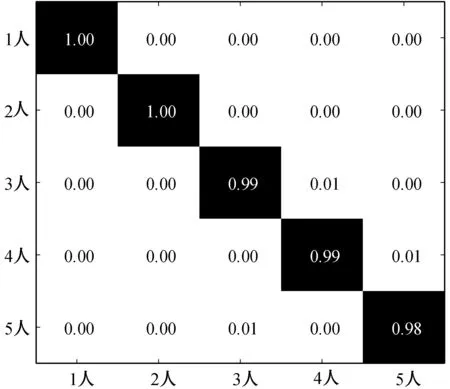
图12 人员静止时人数识别准确率

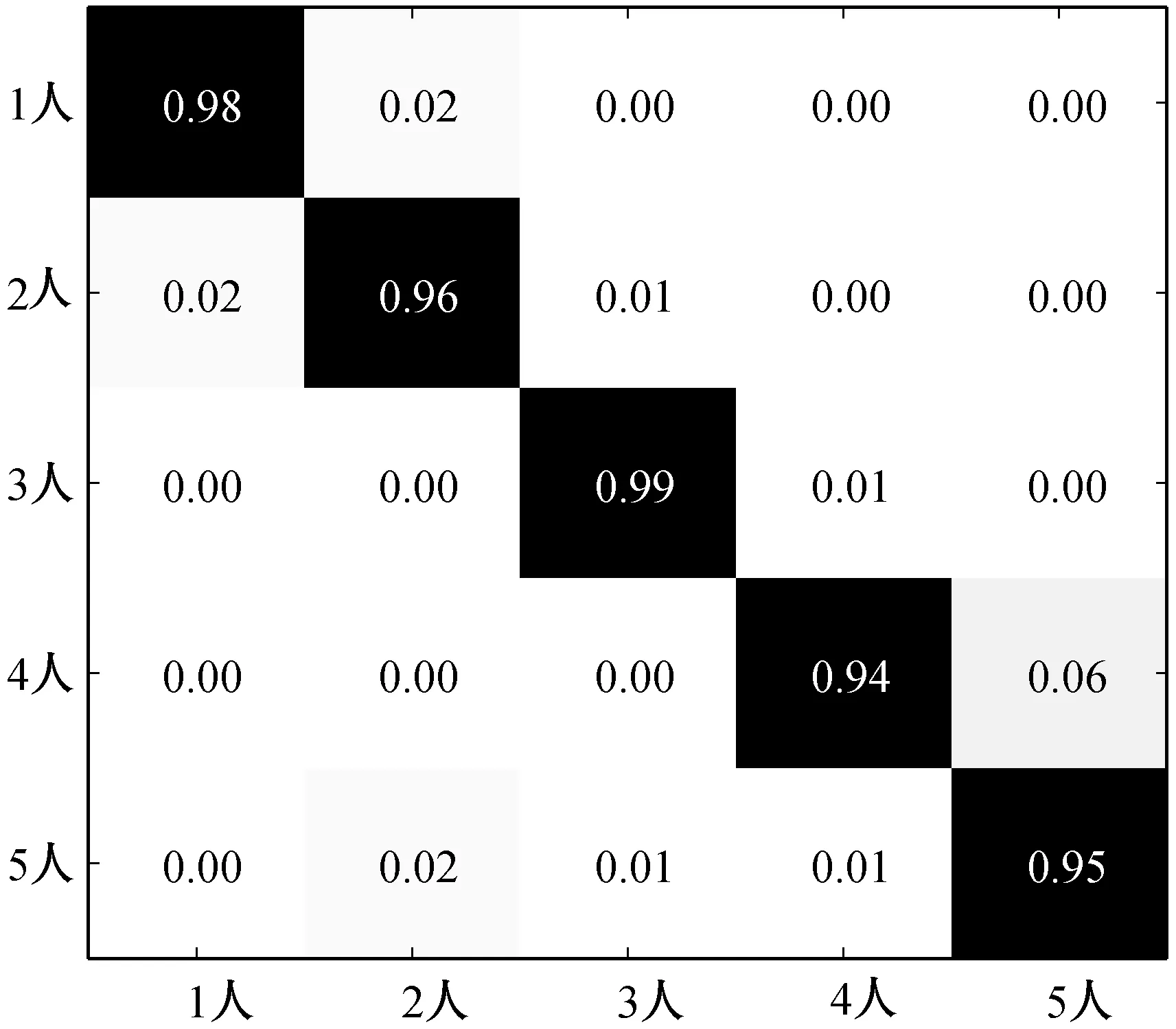
图13 人员随机运动时人数识别准确率

图14列出了本文方法与文献[13-14]中系统在不同人数情况下的识别结果。Trained-once Crowd Counting系统识别率较低，且在人数增多后，识别率下滑严重。FreeCount系统具有不错的识别效果和稳定性，但与本文方法相比，总体识别率低了近3百分点。

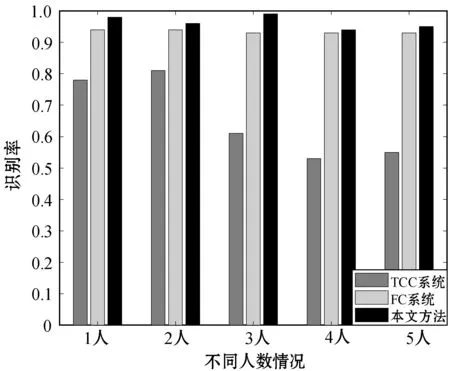
图14 不同人数情况下三种方法的识别率

4 结 语

本文提出的基于信道状态信息的室内人数统计算法有望提供一种低成本、无接触的人数统计方案。所用设备为商用无线路由器，统计人员无须佩戴其他设备。该算法重构了CSI相位，避免了相位杂乱分布的问题；采用Hampel滤波器去除数据中的异常值，保证了数据的准确性；采用PCA进行特征提取，降低了数据维度；在使用多种分类算法进行分类时，实验结果表明基于单层决策树的AdaBoost算法性能最优。