考虑井筒变形的深层射孔井岩石破裂压力计算模型

任 岚 蒋 豪 赵金洲 吴建军 林 然 李 洋

（1.西南石油大学油气藏地质及开发工程国家重点实验室 四川 成都 610500；2.中国石油煤层气有限责任公司 北京 100020）

0 引 言

深层和超深层页岩气的开发已成为中国油气开采的关注热点。相对于浅层页岩储层，深层页岩气储层埋深大、三向主应力高，导致压裂施工过程中水力裂缝起裂压力高，准确预测岩石破裂压力对于压裂施工顺利进行具有重要意义。

分段多簇压裂已成为页岩气开发主体技术［1］，工程实践表明，通过优化射孔参数可以降低岩石破裂压力，从而保障深层地层压裂作业井裂缝的有效起裂。国内外学者［2-16］针对射孔完井岩石破裂压力和裂缝延伸方向的预测进行了大量研究。数值计算破裂压力常采用有限元、边界元和离散元等方法［3-8］分析了射孔方位、布孔方式、射孔密度和射孔深度对地层破裂压力的影响。

实验方面，A.Daneshy［9］采用15.2 cm×15.2 cm×25.4 cm 的石膏，首次进行了射孔条件下水力裂缝起裂的实验研究，并通过少量实验指出射孔深度似乎与破裂压力呈反比。黄中伟等［10］和姜浒等［11］研究得出一定范围内射孔深度与破裂压力呈正相关，这与A.Daneshy 得出的结论相反。除上述数值模拟和实验研究，也有针对射孔完井岩石破裂压力理论模型，如考虑水平分段压裂下单缝和多缝破裂压力理论计算方法［12］以及裂缝性地层射孔完井下岩石破裂压力理论计算公式［13-14］。基于线弹性力学的理论方法有唐世斌等［15］和范勇等［16］提出的圆形井筒对称射孔下地层破裂压力计算方法。二者均将射孔孔眼视为裂缝，并将圆形射孔井筒简化为平面状态下带双裂纹的圆孔问题。本文借鉴其思路，也对裂缝作上述处理。

以上针对射孔井筒岩石破裂压力的讨论均将井筒视为圆形，但测井数据表明，地下井筒形状近似为椭圆形［17-18］，实际钻井中由于剪切作用、应力集中导致井眼扩大，多呈椭圆形态［19］，且深层储层高应力状态下，井筒更易发生变形。因此，研究射孔椭圆形井筒的破裂压力更符合矿场实际。针对椭圆形井筒的研究多侧重于井壁稳定性分析［20-22］，或仅考虑井筒变形下的岩石破裂压力而忽略射孔孔眼的作用［18］。

本文基于保角变换方法和断裂力学理论，考虑椭圆井筒与射孔中液压与远地应力的耦合作用，推导射孔孔眼尖端应力强度因子，结合最大周向应力破坏准则，建立椭圆井筒射孔的岩石破裂压力计算公式，通过模型简化并与现有圆形井筒岩石破裂压力理论计算和实验结果对比，验证模型的正确性，并以此分析井筒变形程度、射孔方位和射孔深度对岩石破裂特征的影响，为深层页岩储层椭圆井筒定向射孔优化提供合理建议。

1 破裂压力计算模型

深层地层钻井过程中由于断层、应力集中等因素，井眼多呈椭圆形。固井时下入套管，并注水泥进行加固，此过程中变形是否稳定仍未可知。因此，本文假定固井时圆形套管仍然受到这些因素的影响，会发生椭圆形变。

实际工程中的井筒直径和射孔深度远大于射孔孔径，因此可忽略射孔孔径的影响，将射孔孔眼简化为裂缝［15-16］。射孔椭圆井筒模型可转化为无限大平面带有双裂缝的椭圆模型，如图1所示。本文假定井筒及地层均符合线弹性，将研究对象视为线弹性材料。

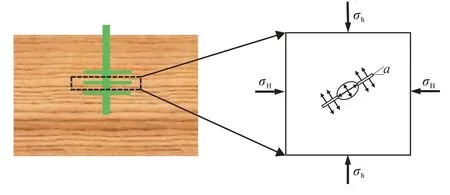
图1 射孔椭圆井筒简化为双裂缝椭圆模型示意Fig.1 Schematic diagram of double-fracture elliptical model simplified by an perforated elliptical wellbore

1.1 应力强度因子计算

根据复变函数理论，引入保角映射函数可将Z平面上的椭圆井筒和射孔孔眼所占的岩石以外的区域映射变换为ζ平面上的中心单位圆内部，椭圆井筒和射孔孔眼的边界变换为单位圆周边界，如图2所示。

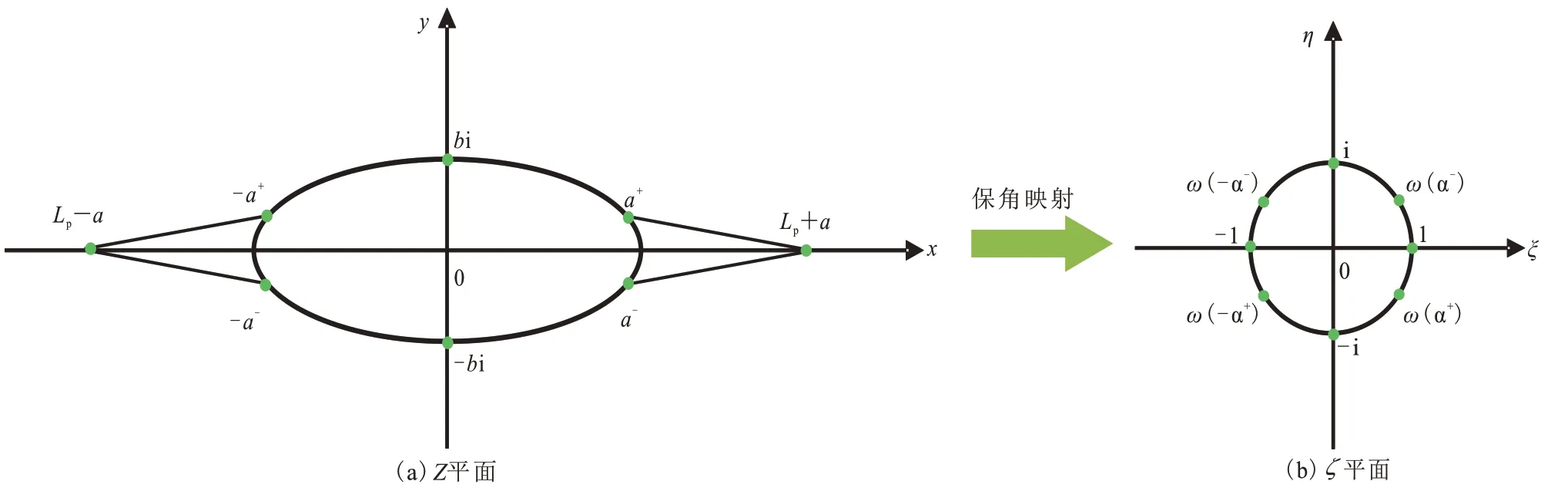
图2 双裂缝椭圆井筒保角映射示意Fig.2 Schematic diagram of conformal mapping of double-fracture elliptical wellbore

引入保角映射函数［23］，可表示为：

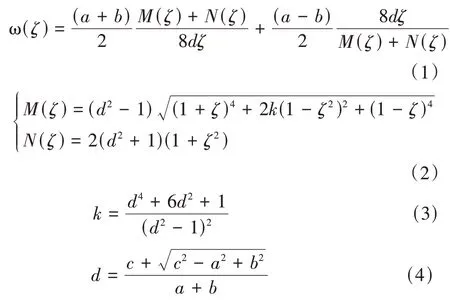
式中：ω(ζ)——映射函数；ζ=ξ+ηi，ξ、η——复平面ζ的坐标分量；a、b——椭圆井筒长半轴、短半轴，m；M(ζ)、N(ζ)、k、d——中间变量；c——射孔深度和椭圆短轴之和，m。

其中c=a+Lp，式中Lp——射孔孔眼深度，m。

应力复变表达式转换为极坐标下复变表达式为：

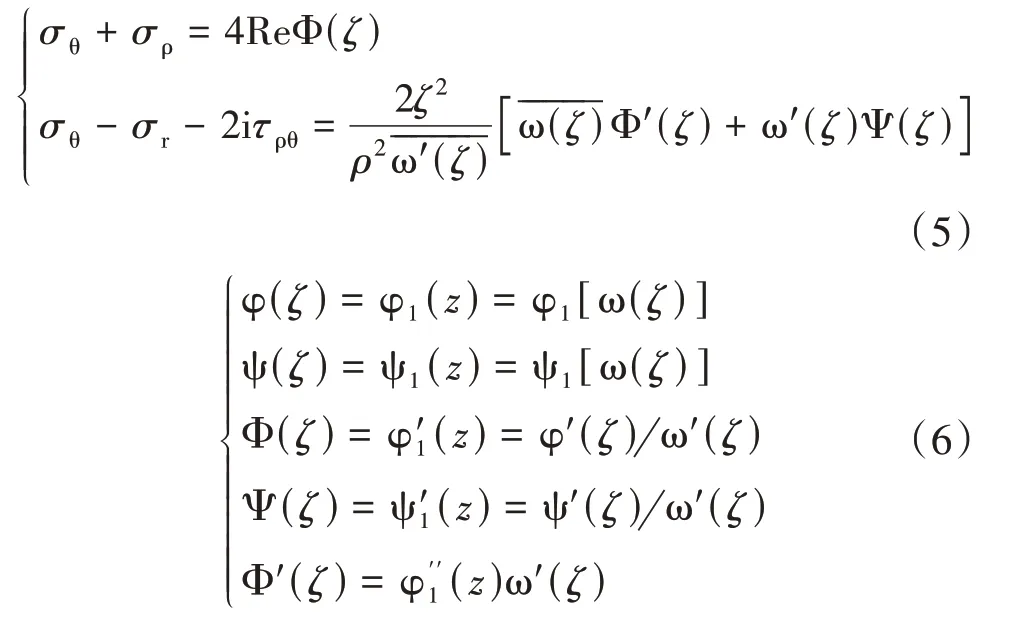
式中：σθ、σρ、τρθ——极坐标下的应力分量，MPa；φ1（z）、ψ1（z）——复变量z（z=x+iy）的解析函数；φ（ζ）、ψ（ζ）、Φ(ζ)、Ψ(ζ)——复变量ζ（ζ=ξ+ηi）的复变应力解析函数；ρ——复平面圆半径，m；Re 表示取负数的实部；上标表示求导符号。

引入记号σ表示ζ平面单位圆上的复数，即σ=eiθ，则复变应力解析函数φ（ζ），ψ（ζ）可表示为：

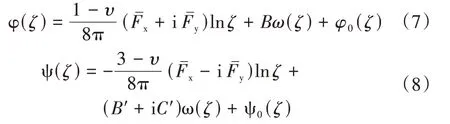
其中

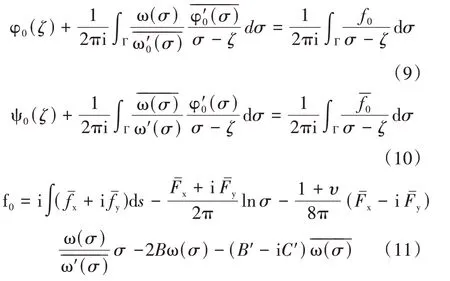
式中：υ——泊松比；、面力和的面力分量，MPa；φ0(ζ)、ψ0(ζ)——复变应力函数分量，MPa；f0——中间变量函数，为σ的已知函数；——ω(σ)的共轭式；B、B′、C′——常数。B和B′- iC′可表示为

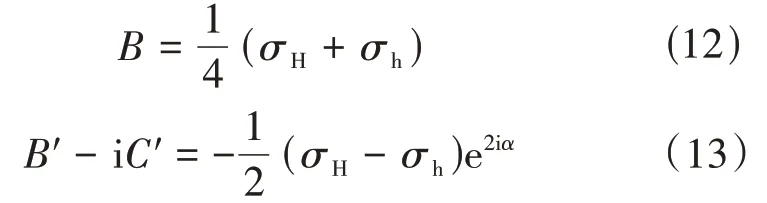
式中：σH、σh——最大、最小水平主应力，MPa；α——射孔孔眼与最大水平主应力之间的夹角，（°）。

根据断裂力学理论，裂缝尖端的应力状态可用应力强度因子表征，引入复应力强度因子，即

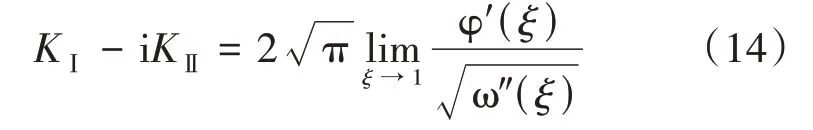
式中：KⅠ、KⅡ——Ⅰ型、Ⅱ型应力强度因子，MPa·m1/2；φ′(ξ)——应力复变解析函数φ(ζ) 的一阶导数；ω″(ξ)——保角映射函数的二阶导数。

椭圆射孔井筒主要受远地应力和井筒液压。由于射孔深度的尺寸较小，可忽略沿孔眼的压力损失。根据线弹性问题的叠加原理，该问题可分为仅受远地应力（加载模式Ⅰ）和仅受井筒液压（加载模式Ⅱ）2 个子问题，如图3所示。

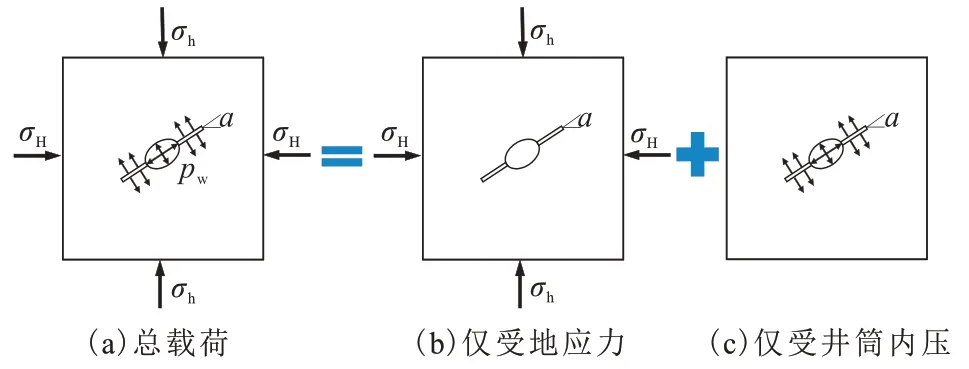
图3 射孔椭圆井筒受力示意Fig.3 Schematic diagrams of forces on perforated elliptical wellbore

（1）加载模式Ⅰ。

于是，加载模式Ⅰ下的应力函数分量可表示为：

式中T——中间变量。

根据柯西积分公式和解析延括定理，对式（17）等式左右两边求导得

因此，结合式（7）、式（18），加载模式Ⅰ下的应力函数的导数φ′I(ζ)为

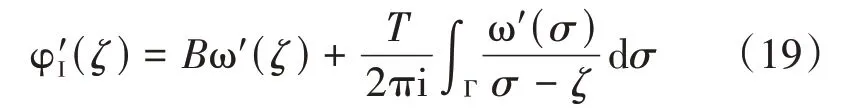
（2）加载模式Ⅱ。

射孔与椭圆井筒内受均匀液压，其面力分量可表示为

式中pw——椭圆井筒与射孔孔眼液压，MPa。

因而面力矢量为

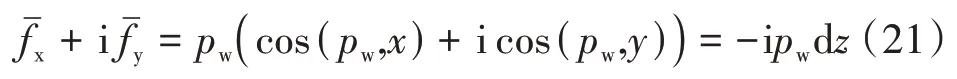
注意到施加于井筒和射孔孔眼的面力为平衡力系，因此== 0，又B=0，B′-iC′=0，且边界上ζ=σ，所以有

与上文推导类似，加载模式Ⅱ下的应力函数的导数φ′II(ζ)为

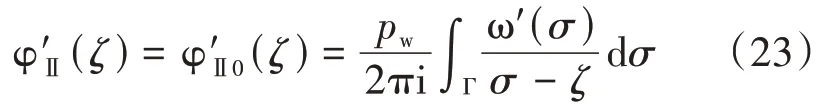
根据叠加原理，将加载模式Ⅰ和加载模式Ⅱ下的应力函数导数相加可得总加载模式下的应力导数φ′(ζ)为

由式（1）知，保角映射函数的一阶导数为

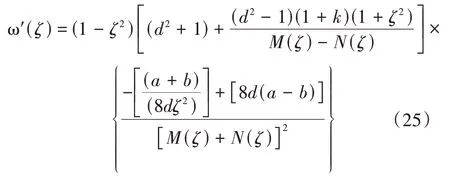
依据无穷远处的柯西积分公式，结合式（25），可得

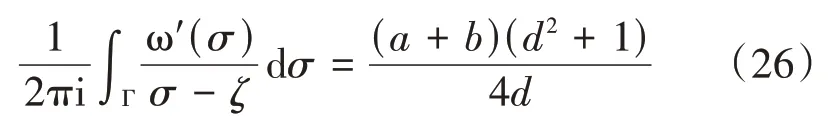
将式（24）、式（25）代入式（14），可得射孔孔眼尖端Ⅰ型、Ⅱ型应力强度因子表达式为：

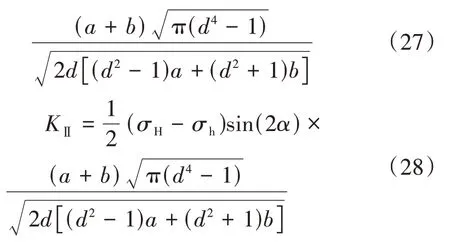
S.D.Hallam 等［24］指出水力裂缝优先起裂于射孔孔眼。因此，只需通过计算射孔孔眼尖端应力强度应子，并结合岩石破裂准则，即可得出岩石破裂压力。

1.2 岩石破裂压力计算

依据断裂力学理论，裂缝尖端某处的周向应力可以表示为

式中：σθ——裂缝尖端某处的周向应力，MPa；θ——裂缝周围某点与裂缝尖端连线与裂缝轴线方向的角度，（°）；r——裂缝周围某点到裂缝尖端的距离，m。

本文采用最大周向应力准则作为岩石破裂判断依据，即当最大周向应力达到最大时，岩石发生破裂，所以有

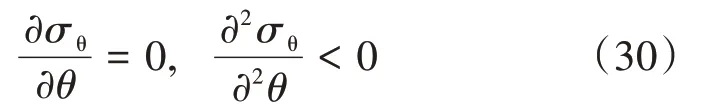
起裂角满足方程

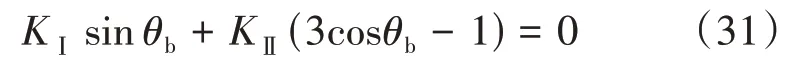
式中θb——水力裂缝起裂角，即起裂缝偏离射孔孔眼的角度，（°）。

由式（30）可得

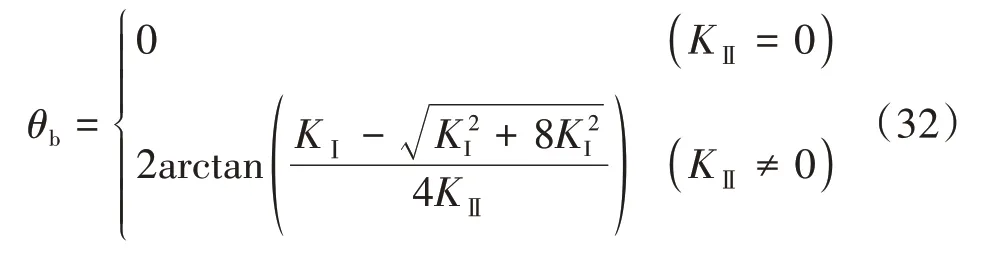
当井筒液压增大至破裂压力时，岩石发生张性破裂。此时，根据断裂力学理论可知，裂缝尖端Ⅰ型应力强度因子等于其Ⅰ型断裂韧性，即

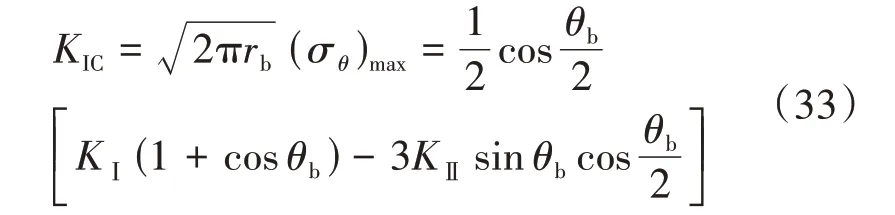
式中：KIC——岩石Ⅰ型断裂韧性，MPa·m1/2；rb——射孔尖端起裂缝的长度，m。

将式（27）、式（28）代入式（33），可得射孔孔眼尖端岩石破裂压力为

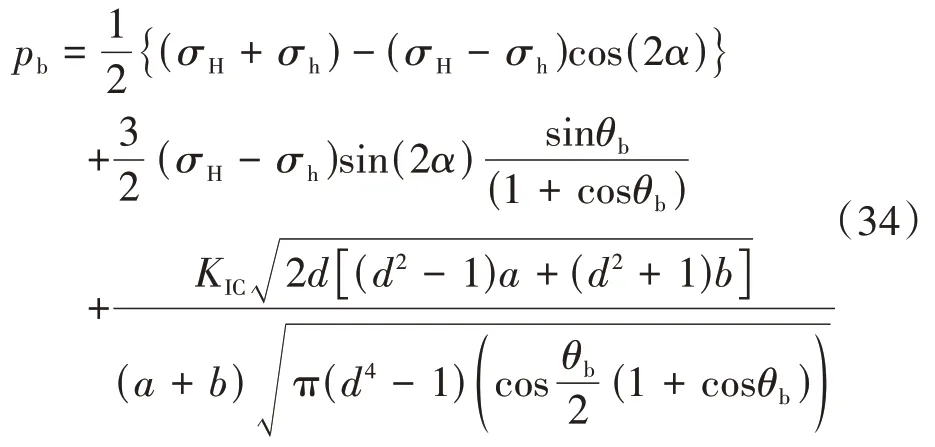
式中pb——射孔尖端岩石破裂压力，MPa。

2 模型验证

据调研，目前尚未有文献报道椭圆井筒定向射孔岩石破裂压力计算方法，但已有唐世斌等［15-16］报道了圆形井筒定向射孔岩石破裂的计算模型与实验研究。因此，本文采用改变椭圆井筒长短轴比值使其接近圆形井筒的方式进行计算，并与文献中考虑圆形井筒的计算结果和实验结果对比，以此验证模型的有效性。

首先，当椭圆井筒长半轴a趋近于短半轴b时，d趋近于a/c，参考唐世斌等［15］的基础数据，即最大水平主应力为4 MPa，最小水平主应力为2 MPa，射孔深度为20 mm，岩石断裂韧性为2.1 MPa·m1/2，圆形井筒半径为50 mm，本文取椭圆井筒长半轴为50 mm，长短轴之比为1.1 进行计算，对比结果如图4所示。结果表明，唐世斌等［15］的结果在整个射孔方位角范围或大或小，但相对误差均小于5%，整体趋势一致。出现该现象的原因可能是该文采用经验公式计算射孔尖端岩石Ⅱ型应力强度因子，计算存在误差。范勇等［16］的结果与本文计算的理论值相对误差均小于2%，具有良好的一致性。

图4 3种理论方法计算的射孔方位角与破裂压力关系Fig.4 Relations between perforation azimuth and fracture pressure calculated by 3 theoretical methods

其次，Y.J.Zeng 等［25］采用长度为30 cm 的人造立方试样，进行了圆形井筒定向射孔下岩石破裂压力试验，试验选择直径为15 mm 钢管模拟套管，预留30 mm 的小孔模拟射孔孔眼，试验的加载条件为最小水平主应力为1 MPa，最大水平主应力为4 MPa。通过改变椭圆井筒长短轴比值，使其无限接近圆形井筒，利用试验中的基础数据，进行了破裂压力的理论计算，并与试验结果对比，如图5所示。

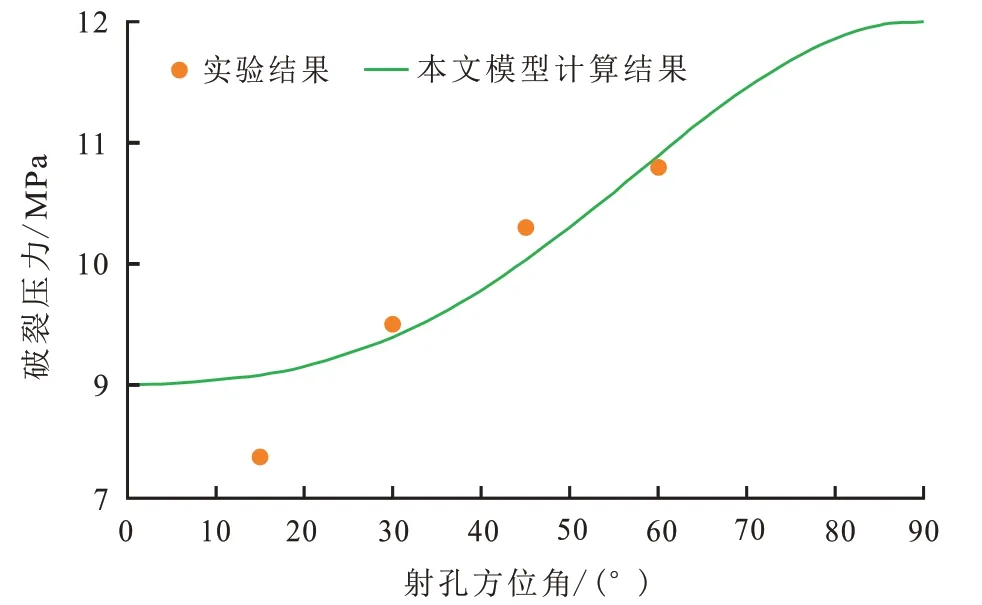
图5 模型计算、试验结果的射孔方位角与破裂压力关系Fig.5 Relations between perforation azimuth and breakdown pressure based on model calculation and tested results

由图5可知，理论计算的破裂压力与文献给出的4 个试验点相对误差分别为8.41%、1.31%、2.99%、0.91%，理论值与试验值吻合较好。射孔方位角为15°时，理论值与试验值的相对误差超过5%，究其原因可能是不同试样结构的非均质性导致的离散试验数据。

综上对比可知，本文提出的椭圆井筒模型取极限值，使井筒形状近似为圆形，其计算的理论值与文献中的结果具有良好的一致性，且与试验结果整体趋势一致，从而说明模型的可靠性。

3 岩石破裂的影响因素

水力压裂射孔参数是影响岩石破裂的重要因素，合理的射孔参数可有效降低破裂压力，减小近井附近裂缝弯曲度，降低施工风险。因此，本文利用提出的射孔椭圆井筒岩石破裂压力预测模型，参考唐世斌、范勇等人理论计算的基础数据，设置最大水平主应力为5 MPa，最小水平主应力为2 MPa，椭圆井筒长半轴a为40 mm，短半轴b为20 mm，射孔深度Lp=40 mm，岩石Ⅰ型断裂韧性KIC=2.3 MPa·m1/2，开展井筒变形程度、射孔方位、射孔深度对岩石破裂特征影响的深入研究。

3.1 井筒变形

深层页岩储层埋深大，三向主应力高，加之储层或存在复杂构造等因素，多数井筒存在一定程度变形。测井资料表明，深层地层变形井筒形状主要为椭圆形。地层破裂压力除了与地层本身的性质相关外，更与地层所在的应力密切相关。研究表明，井筒变形将导致其周围的地层应力状态产生变化。为了研究井筒极限变形程度对岩石破裂特征的影响，利用椭圆井筒长短轴长度比值表征井筒变形程度。选定井筒短半轴b为20 mm，计算了椭圆井筒长短轴之比为2、3、4、5 时岩石的破裂压力和起裂角。同时也计算正常变形下（即长短轴之比为1.2）破裂压力和起裂角的变化。

图6给出了不同椭圆井筒长短轴之比下的破裂压力。结果表明，随着椭圆长短轴比值的增加，破裂压力减小。即井筒的变形程度越大，射孔孔眼尖端裂缝起裂的破裂压力越小，但降低的幅度逐渐减小。例如，射孔方位α=0°，算例中由于井筒变形程度造成的破裂压力差异达1.63 MPa，且长短轴之比r=1.2 增至2，由r=2 每递增1 至5 时，破裂压力分别减小0.53、0.47、0.36 、0.27 MPa。因为井筒变形程度增加，井筒纵向方向对射孔孔眼尖端应力集中效应的影响被削弱，这与单一平面裂缝产生的诱导应力场的作用规律类似，即随着裂缝高度的减小，裂缝产生的应力阴影将减小。因此，受井筒变形的影响，将井筒考虑为圆形时将高估岩石破裂压力，根据李军等［26］报道的实际工况下井筒长短轴之比为1.2～1.5，该算例下非变形井筒下的破裂压力相较于椭圆井筒偏高2.3%～5.6%。尽管将井筒考虑为圆形，预测的破裂压力稍高，有利于压裂设计。但是这一原则仅限于井口具有较大压力窗口时适用，且由于按照高破裂压力值进行设计，压裂液、压裂设备的选择上势必会加大成本投入，这与降本增效的理念相违背。对于超深地层的压裂施工而言，地层破裂压力较大，井口留出的压力窗口本身较窄，若过高估计破裂压力，一般而言需降低施工排量，保证井口不超压。低排量将严重影响深层地层缝网的建造，且对后续施工措施（如暂堵转向）调整带来挑战。

图6 不同长短轴比射孔方位角与破裂压力关系Fig.6 Relations between perforation angle and breakdown pressure with different length ratios of major axis to minor axis

图7给出了不同椭圆井筒长短轴之比下的起裂角。结果表明，任意射孔方位角下，射孔孔眼尖端水力裂缝起裂角随椭圆长短轴比值的增加而增加。

图7 不同长短轴比射孔方位角与起裂角关系Fig.7 Relations between perforation angle and initiation angle with different length ratios of major axis to minor axis

具体可分为以下区域：射孔方位角为0°～5°，起裂角受井筒变形的影响较小，起裂角的变化为0°～2°，且起裂角均小于8°，裂缝基本沿最大主应力方向起裂，近井筒裂缝弯曲程度低；当射孔方位角为5°～45°时，起裂角受井筒变形的影响较大，长短轴之比由2 增至5，起裂角起伏达到7°，起裂角达43°，近井筒裂缝弯曲大。由此可知，井筒变形程度的增加导致射孔孔眼尖端剪切作用增加，更易形成剪切裂缝，可能造成砂堵、施工压力突升。因此，从岩石破裂的角度讲，井筒变形有利于射孔尖端裂缝起裂，但从后续压裂施工而言，它将导致近井筒裂缝弯曲较大，造成施工压力增大。

3.2 射孔方位

由于钻井作业、地应力方位难以精确测定等复杂因素，往往射孔孔眼并不完全垂直于最小水平主应力。本文将射孔轴线与最大水平主应力之间的夹角α为射孔方位角。为分析射孔方位角对岩石破裂特征的影响，计算了射孔方位角为0°～90°时岩石破裂压力和起裂角。

由图8可知，井筒形状仅影响破裂压力的高低，不改变曲线趋势。由于井筒变形，椭圆井筒长轴方向应力集中，进而导致其裂缝尖端破裂压力较圆形井筒低。总体而言，破裂压力随射孔方位角的增加而增加。根据曲线上升的速度可将其影响分为3 个区域。

图8 射孔方位角与破裂压力关系Fig.8 Relations between perforation azimuth and breakdown pressure

第1 区域：射孔方位角为α为0°～20°时，岩石破裂压力随射孔方位角的增加呈平缓上升趋势，相对于最小破裂压力6.64 MPa 而言，仅增幅1%，与陈峥嵘等［27］优化的射孔方位0°～15°的结果基本吻合。

第2 区域：射孔方位角α为20°～80°时，岩石破裂压力随射孔方位角的增加呈直线上升趋势，增幅达到41.3%。

第3 区域：射孔方位角α为80°～90°，岩石破裂压力增加幅度不明显。因此，使射孔孔眼与最大水平主应力之间的夹角保持在0°～20°，可避免岩石破裂压力急剧升高，这对于深层页岩的水力压裂施工具有重要意义。

图9显示了射孔方位对裂缝起裂角的影响。结果表明，椭圆形井筒和圆形井筒射孔尖端水力裂缝起裂角均随射孔方位角α的增加先增大后减小。因为椭圆形射孔尖端剪切效应更明显，相较于圆形井筒，椭圆形井筒下岩石起裂角度最大高出4°。射孔方位角α为0°和90°时，按式（30）计算，裂缝尖端Ⅱ型应力强度因子为0，裂缝为纯张性裂缝，因而其起裂角均为0°，此时水力裂缝形成平面缝；而射孔方位为45°时，根据弹性力学理论可知，此时裂缝所受的剪应力最大，裂缝剪切破坏严重，因而裂缝起裂角最大，导致近井筒弯曲摩阻增大，施工压力增加。因此，宜选取射孔方位角为0°～20°，保证施工的顺利实施。

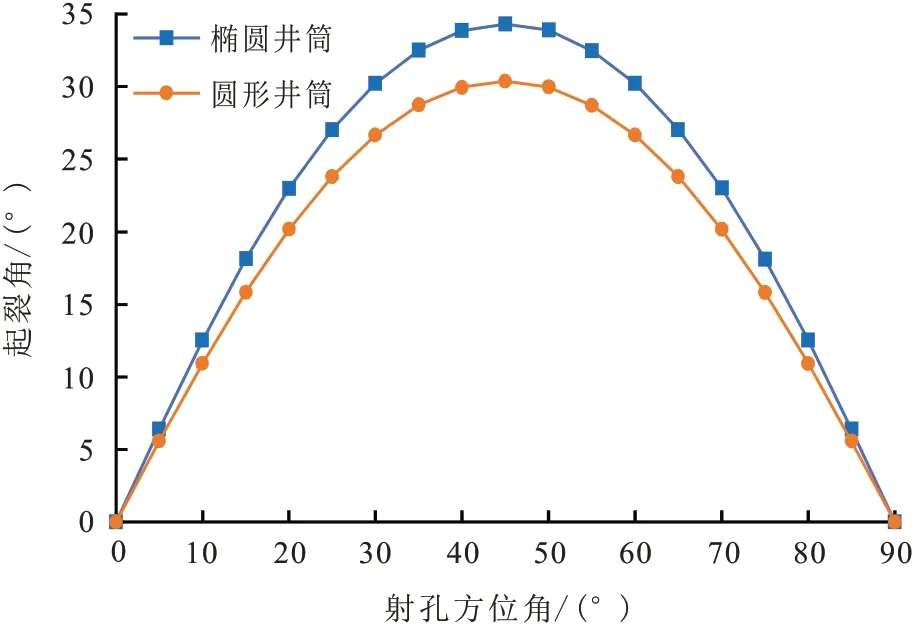
图9 射孔方位角与起裂角关系Fig.9 Relations between perforation azimuth and initiation angle

3.3 射孔深度

射孔深度是影响射孔效果的直接因素，合理的射孔深度可有效解除近井筒的地层污染，降低岩石破裂压力。为了研究射孔深度对岩石破裂特征的影响，选取射孔深度10～80 mm 计算破裂压力和起裂角，如图10、图11 所示。

图10 不同射孔深度下射孔方位角与破裂压力关系Fig.10 Relations between perforation azimuth and breakdown pressure in different perforated depths

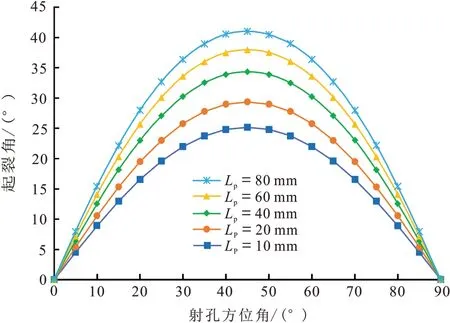
图11 不同射孔深度下射孔方位角与起裂角关系Fig.11 Relations between perforation azimuth and initiation angle in different perforated depths

由图10 可知，增加射孔深度可降低岩石破裂压力。射孔方位角为90°时，射孔深度Lp=10 mm 增至40 mm，破裂压力降低1.9 MPa；而射孔深度Lp=40 mm 增至80 mm，降幅仅为0.8 MPa。由此可知，射孔深度小于井筒尺寸前（长半轴40 mm，短半轴20 mm），破裂压力受其影响相对较大，而射孔深度大于井筒尺寸后，破裂压力随射孔深度的增加其减小的幅度逐渐减小。由图11 可知，与其对岩石破裂压力的影响规律相反，水力裂缝起裂角随射孔深度的增加而增加，但增加的幅度逐渐减小。射孔方位角为45°时，射孔深度Lp=20 mm 增至40 mm，起裂角增幅16.9%；而射孔深度Lp=60 mm 增至80 mm，增幅仅为8%，这与唐世斌等［15］得出的规律一致。因此，对于给定射孔方位、应力条件下，存在一个合理的射孔深度，使其既能有效降低破裂压力，又能避免近井筒裂缝弯曲程度。综合考虑，保证起裂角小于15°和破裂压力最大降幅25%的前提下，本文建议最优的射孔深度为椭圆井筒短轴的1.5～2.0 倍，尽管较张广清等［6］和范勇等［16］给出的2～3 倍相对保守，但该范围考虑了降低近井裂缝弯曲的因素。

3.4 工程实例

为了说明模型的工程实用性，以川东南海相深层页岩气探井PS1 井为例，计算了该井压裂层位破裂压力。该井位于四川盆地川东隔挡式褶皱带黄泥塘高陡构造带宝顶—1 潜伏构造，属于为预探直井，试气井段5 957.50 ～5 960.50 m，其原始地层压力为92.3 MPa， 地层最小水平主应力为132.7 MPa，最大水平主应力为145.2 MPa，地层有效应力系数（Biot 系数）取0.1。该井采用油管带封隔器管柱压裂，井筒外径206.4 mm，射孔深度为100 mm。岩石力学参数测试显示该试气段Ⅰ类泥页岩的Ⅰ型断裂韧性为1.35 MPa·m1/2。

根据该井压裂施工曲线（图12）得到地表的破裂压力为106.1 MPa，折算到地下的破裂压力为135.8 MPa。由于未获得该井的井径测井资料，且李军等报道的实际工况下井筒长短轴之比常为1.2～1.5。本算例取井筒长短轴比1.2 和1.5，并取式（34）中的应力为有效应力，则本文模型计算出的结果分别为137.62、137.44 MPa，与实际相差1.34%、1.21%；而传统圆形井筒模型计算出的结果为143.10 MPa，与实际相差5.38%，新模型较实际值更接近，从而进一步说明本文提出的模型的可靠性与实用性。

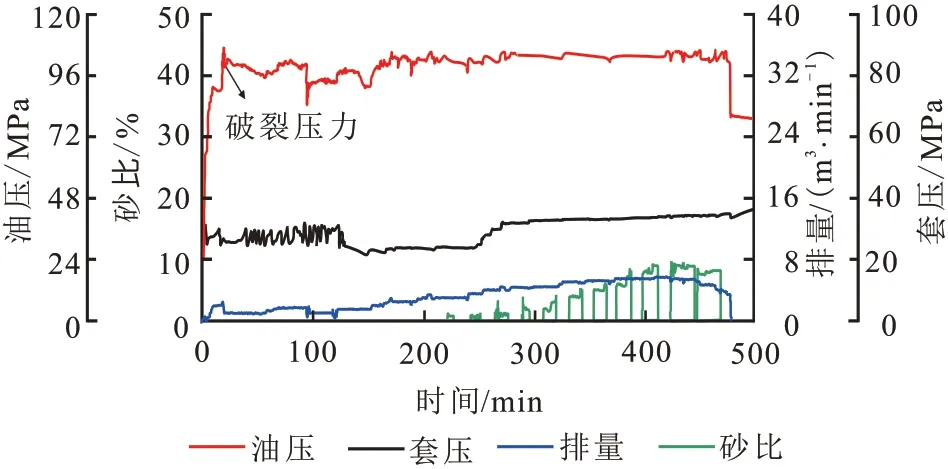
图12 PS1井压裂施工曲线Fig.12 Fracturing operation curves for Well PS1

4 结 论

（1）基于保角变换方法、复变函数和断裂力学理论，考虑深层地层井筒更易变形的实际情况，建立了射孔椭圆井筒岩石破裂压力计算模型，通过理论与实验结果对比，验证了模型的可靠性，为变形井筒的射孔井破裂压力计算提供了新的方法。

（2）对比分析表明，考虑井筒非变形状态下所预测的破裂压力偏高；破裂压力随井筒变形程度的增加而降低，裂缝起裂角则增加。

（3）射孔方位和射孔深度对岩石破裂压力和起裂角均有较大影响。随射孔方位角的增大，破裂压力增加，起裂角则先增加后降低；随着射孔深度的增加，破裂压力降低且幅度逐渐减小，而起裂角则增加。

（4）综合降低破裂压力和避免近井裂缝弯曲度过大两方面因素，推荐最优射孔方位角小于20°，最优射孔深度为井筒尺寸的1.5～2.0 倍。